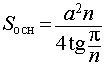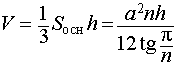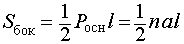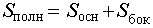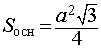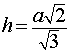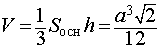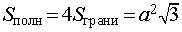В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии в пространстве, которые относятся к исследованию пирамиды. Обычно в такой задаче нужно найти длины ребер, углы между ребрами, уравнения граней пирамиды и их площади, объем пирамиды, угол между ребром и гранью, уравнение высоты, длину высоты пирамиды и т.д.
- Решения задачи о пирамиде онлайн
- Онлайн решение Пирамиды по координатам вершин
- Пирамиды. Правильные пирамиды. Теорема Эйлера. Формулы для объема, площади боковой поверхности и площади полной поверхности пирамиды
- Пирамиды
- Правильные пирамиды. Свойства правильной пирамиды
- Тетраэдры. Правильные тетраэдры
- Формулы для объема, площади боковой и полной поверхности пирамиды
- 🎦 Видео
Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
Решения задачи о пирамиде онлайн
Задача 1. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.
Задача 2. Даны координаты вершин пирамиды $$A(12;11;17), B(14;12;14), C(13;14;15), D(12;21;12).$$ Найти:
— объем пирамиды;
— площадь грани $ABC$;
— уравнение плоскости, проходящей через точки $B,C,D$;
— длину высоты пирамиды, опущенной на грань $ABC$.
Задача 3. Пирамида $АВСD$ задана координатами своих вершин: $$А(4, -1,0), B(2, 3, 4), C(-1, 4, 1), D(4, -3, 5).$$ Найдите:
1. угол между ребрами $АВ$ и $АС$,
2. уравнение ребра $АВ$,
3. уравнение грани $АВС$,
4. уравнение высоты, опущенной из вершины $D$, на грань $АВС$,
5. выясните, образуют ли векторы $АВ, АС, АD$ линейно независимую систему,
6. координаты вектора $MN$, если $М$ – середина ребра $AD$, $N$ – середина ребра $ВC$,
7. разложите вектор $MN$ по базису $AB, AC, AD$, если он таковым является.
Видео:Подсчёт количества граней и рёбер у трёхмерных фигур | Фигура | ГеометрияСкачать
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать  Пирамиды. Правильные пирамиды. Теорема Эйлера. Формулы для объема, площади боковой поверхности и площади полной поверхности пирамиды
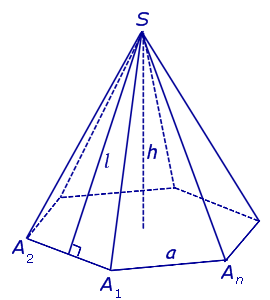
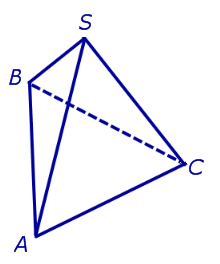
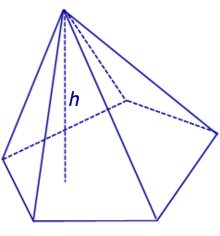
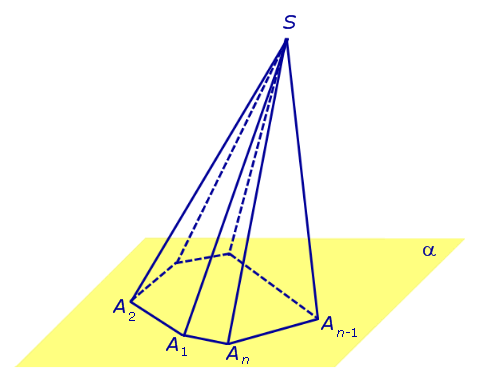
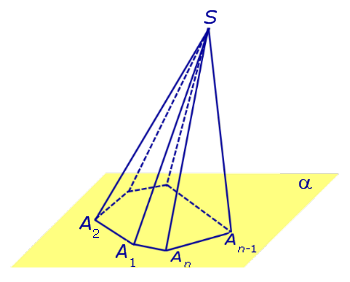
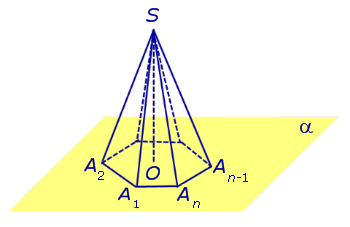
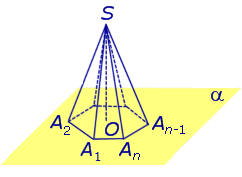
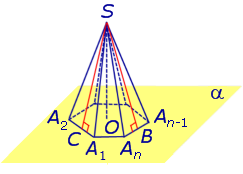
Видео:10 класс, 32 урок, ПирамидаСкачать  ПирамидыРассмотрим произвольную плоскость α , произвольный выпуклый n – угольник A1A2 . An , расположенный в этой плоскости, и точку S , не лежащую в плоскости α . Определение 1. Пирамидой ( n — угольной пирамидой) называют фигуру, образованную отрезками, соединяющими точку S со всеми точками многоугольника A1A2 . An (рис. 1) .
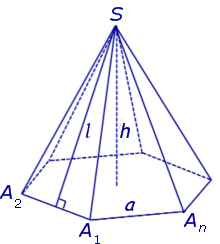
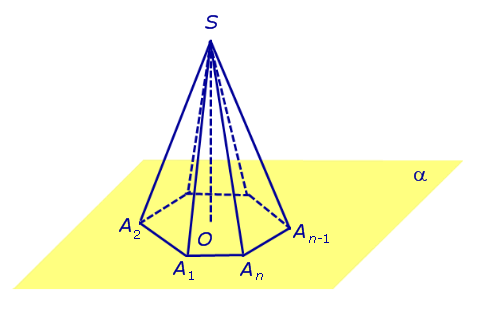
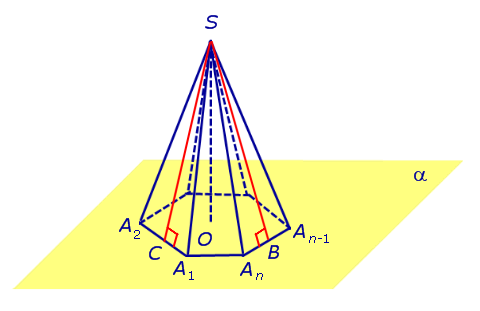
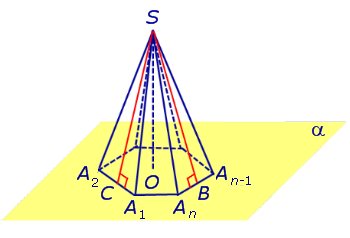
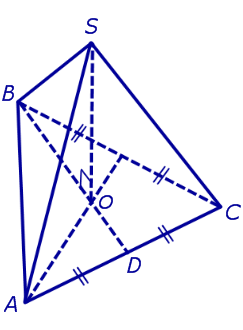
Доказательство. Заметим, что у n — угольной пирамиды (n + 1) вершина, n боковых граней, 1 основание, n ребер основания и n боковых ребер. Следовательно, у n — угольной пирамиды (n + 1) грань и 2n ребер. то теорема Эйлера доказана. Видео:10 класс, 33 урок, Правильная пирамидаСкачать  Правильные пирамиды. Свойства правильной пирамиды
Замечание 2. Если центр основания A1A2 . An правильной пирамиды SA1A2 . An обозначить буквой O , то длина отрезка SO будет равняться высоте пирамиды. Часто и сам отрезок SO называют высотой пирамиды, опущенной из вершины S . Определение 4. Высоту боковой грани правильной пирамиды, опущенную из вершины S , называют апофемой .
На рисунке 3 отрезок SB – апофема грани SAnAn-1 и отрезок SC – апофема грани SA2A1 . Замечание 3 . У любой правильной n – угольной пирамиды можно провести n апофем. Свойства правильной пирамиды:
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности пирамиды :
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пирамиды. Теорема Эйлера для пирамид
,
.
,
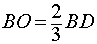
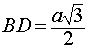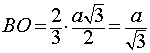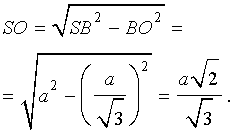
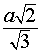
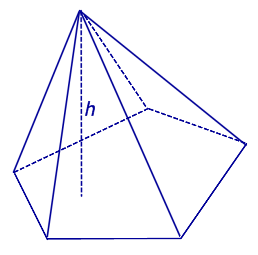
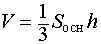