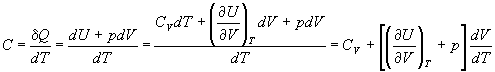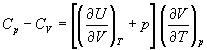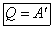Первое начало термодинамики в дифференциальной и интегральной форме уравнение адиабаты

Первый закон (первое начало) термодинамики — это, фактически, закон сохранения энергии. Он утверждает, что

энергия изолированной системы постоянна. В неизолированной системе энергия может изменяться за счет: а) совершения работы над окружающей средой; б) теплообмена с окружающей средой.

Для описания этих изменений вводят функцию состояния — внутреннюю энергию U и две функции перехода — теплоту Q и работу A. Математическая формулировка первого закона:

dU = Q — A (дифференциальная форма) (2.1)

U = Q — A (интегральная форма) (2.2)

Буква в уравнении (2.1) отражает тот факт, что Q и A — функции перехода и их бесконечно малое изменение не является полным дифференциалом.

В уравнениях (2.1) и (2.2) знаки теплоты и работы выбраны следующим образом. Теплота считается положительной, если она передается системе. Напротив, работа считается положительной, если она совершается системой над окружающей средой.

Существуют разные виды работы: механическая, электрическая, магнитная, поверхностная и др. Бесконечно малую работу любого вида можно представить как произведение обобщенной силы на приращение обобщенной координаты, например:

A_мех = p . dV; A_эл = . dе; A_пов = . dW (2.3)

( — электрический потенциал, e — заряд, — поверхностное натяжение, W — площадь поверхности). С учетом (2.3), дифференциальное выражение первого закона можно представить в виде:

dU = Q — p . dV A_немех (2.4)

В дальнейшем изложении немеханическими видами работы мы будем, по умолчанию, пренебрегать.

Механическую работу, производимую при расширении против внешнего давления p_ex, рассчитывают по формуле:

A = 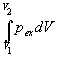(2.5)

Если процесс расширения обратим, то внешнее давление отличается от давления системы (например, газа) на бесконечно малую величину: p_ex = p_in — dp и в формулу (2.5) можно подставлять давление самой системы, которое определяется по уравнению состояния.

Проще всего рассчитывать работу, совершаемую идеальным газом, для которого известно уравнение состояния p = nRT / V (табл. 1).

Таблица 1. Работа идеального газа в некоторых процессах расширения V₁ V₂:

Процесс

Расширение в вакуум

Расширение против постоянного внешнего давления p

p (V₂—V₁)

Изотермическое обратимое расширение

nRT ln(V₂/V₁)

Адиабатическое обратимое расширение

nC_V(T₁—T₂)

При обратимом процессе совершаемая работа максимальна.

Теплота может переходить в систему при нагревании. Для расчета теплоты используют понятие теплоемкости, которая определяется следующим образом:

C = 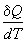(2.6)

Если нагревание происходит при постоянном объеме или давлении, то теплоемкость обозначают соответствующим нижним индексом:

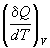
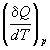
C_V = ; C_p = . (2.7)

Из определения (2.6) следует, что конечную теплоту, полученную системой при нагревании, можно рассчитать как интеграл:

Q = 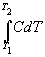(2.8)

Теплоемкость — экспериментально измеряемая экстенсивная величина. В термодинамических таблицах приведены значения теплоемкости при 298 К и коэффициенты, описывающие ее зависимость от температуры. Для некоторых веществ теплоемкость можно также оценить теоретически методами статистической термодинамики (гл. 12). Так, при комнатной температуре для одноатомных идеальных газов мольная теплоемкость C_V = 3/2 R, для двухатомных газов C_V = 5/2 R.

Теплоемкость определяется через теплоту, переданную системе, однако ее можно связать и с изменением внутренней энергии. Так, при постоянном объеме механическая работа не совершается и теплота равна изменению внутренней энергии: Q_V = dU, поэтому

C_V = 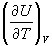. (2.9)

При постоянном давлении теплота равна изменению другой функции состояния, которую называют энтальпией:

Q_p = dU + pdV = d (U+pV) = dH, (2.10)

где H = U+pV — энтальпия системы. Из (2.10) следует, что теплоемкость C_p определяет зависимость энтальпии от температуры.

C_p = 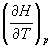. (2.11)

Из соотношения между внутренней энергией и энтальпией следует, что для моля идеального газа

Внутреннюю энергию можно рассматривать, как функцию температуры и объема:

(2.13)

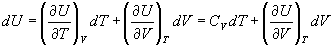
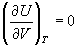
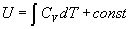
Для идеального газа экспериментально обнаружено, что внутренняя энергия не зависит от объема, , откуда можно получить калорическое уравнение состояния:

(2.14)

В изотермических процессах с участием идеального газа внутренняя энергия не изменяется, и работа расширения происходит только за счет поглощаемой теплоты.

Возможен и совсем иной процесс. Если в течение процесса отсутствует теплообмен с окружающей средой ( Q = 0), то такой процесс называют адиабатическим. В адиабатическом процессе работа может совершаться только за счет убыли внутренней энергии. Работа обратимого адиабатического расширения идеального газа:

A = — U = nC_V (T₁—T₂) (2.15)

(n — число молей, C_V — мольная теплоемкость). Эту работу можно также выразить через начальные и конечные давление и объем:

A = 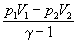(2.16)

где = C_p / C_V.

При обратимом адиабатическом расширении идеального газа давление и объем связаны соотношением (уравнением адиабаты):

pV = const. (2.17)

В уравнении (2.17) важны два момента: во-первых, это уравнение процесса, а не уравнение состояния; во-вторых, оно справедливо только для обратимого адиабатического процесса. Это же уравнение можно записать в эквивалентном виде:

TV -1 = const, (2.18)

T p 1- = const. (2.19)

ПРИМЕРЫ

Пример 2-1. Рассчитайте изменение внутренней энергии гелия (одноатомный идеальный газ) при изобарном расширении от 5 до 10 л под давлением 196 кПа.

Решение. p₁ = p₂ = 196 кПа, V₁ = 5 л, V₂ = 10 л. Начальная и конечная температуры: T₁ = p₁V₁ / nR, T₂ = p₂V₂ / nR. Изменение внутренней энергии идеального газа определяется только начальной и конечной температурой (C_V = 3/2 nR — идеальный одноатомный газ):

U = C_V (T₂—T₁) = 3/2 nR (T₂—T₁) = 3/2 (p₂V₂ — p₁V₁) = 3/2 (196 . 10 3 ) (10-5) . 10 -3 =
= 1470 Дж.

Пример 2-2. Используя первый закон и определение теплоемкости, найдите разность изобарной и изохорной теплоемкостей для произвольной термодинамической системы.

Решение. В определение теплоемкости (2.6) подставим дифференциальное представление первого закона (2.1) и используем соотношение (2.13) для внутренней энергии как функции температуры и объема:

Отсюда при постоянном давлении получаем:

Пример 2-3. Один моль ксенона, находящийся при 25 о С и 2 атм, расширяется адиабатически: а) обратимо до 1 атм, б) против давления 1 атм. Какой будет конечная температура в каждом случае?

Решение. а) Исходный объем ксенона (n = 1):

Конечный объем можно найти из уравнения адиабаты (для одноатомного идеального газа = C_p / C_V = 5/3):

Конечную температуру находим по уравнению состояния идеального газа (p₂ = 1 атм):

б) При необратимом расширении против постоянного внешнего давления уравнение адиабаты неприменимо, поэтому надо воспользоваться первым законом термодинамики. Работа совершается за счет убыли внутренней энергии:

A = — U = nC_V (T₁—T₂),

где n = 1, C_V = 3/2 R (одноатомный идеальный газ). Работа расширения против постоянного внешнего давления p₂ равна:

Приравнивая последние два выражения, находим температуру T₂:

Температура выше, чем при обратимом расширении, т.к. в обратимом случае совершается бМльшая работа, расходуется больше внутренней энергии и температура понижается на большую величину.

Ответ. а) 225 К; б) 238 К.

Пример 2-4. Один моль водяных паров обратимо и изотермически сконденсировали в жидкость при 100 о С. Рассчитайте работу, теплоту, изменение внутренней энергии и энтальпии в этом процессе. Удельная теплота испарения воды при 100 о С равна 2260 Дж/г.

Решение. В процессе

H₂O_(г) H₂O_(ж)

произошло обратимое сжатие газа при постоянном давлении p = 1 атм от объема V₁ = nRT / p = 0.082 . 373 = 30.6 л до объема одного моля жидкой воды V₂

0.018 л. Работа сжатия при постоянном давлении равна:

A = p (V₂—V₁) —pV₁ = -101.3 кПа 30.6 л = -3100 Дж.

При испарении одного моля воды затрачивается теплота 2260 Дж/г 18 г = 40700 Дж, поэтому при конденсации одного моля воды эта теплота, напротив, выделяется в окружающую среду:

Изменение внутренней энергии можно рассчитать по первому закону:

U = Q — A = -40700 — (-3100) = -37600 Дж,

а изменение энтальпии — через изменение внутренней энергии:

H = U + (pV) = U + p V = U + A = Q = -40700 Дж.

Изменение энтальпии равно теплоте, т.к. процесс происходит при постоянном давлении.

Ответ. A = -3100 Дж, Q = H = -40700 Дж, U = -37600 Дж.

ЗАДАЧИ

2-1. Газ, расширяясь от 10 до 16 л при постоянном давлении 101.3 кПа, поглощает 126 Дж теплоты. Определите изменение внутренней энергии газа.

2-2. Определите изменение внутренней энергии, количество теплоты и работу, совершаемую при обратимом изотермическом расширении азота от 0.5 до 4 м 3 (начальные условия: температура 26.8 о С, давление 93.2 кПа).

2-3. Один моль идеального газа, взятого при 25 o C и 100 атм, расширяется обратимо и изотермически до 5 атм. Рассчитайте работу, поглощенную теплоту, U и H.

2-4. Рассчитайте изменение энтальпии кислорода (идеальный газ) при изобарном расширении от 80 до 200 л при нормальном атмосферном давлении.

2-5. Какое количество теплоты необходимо для повышения температуры 16 г кислорода от 300 до 500 К при давлении 1 атм? Как при этом изменится внутренняя энергия?

2-6. Объясните, почему для любой термодинамической системы C_p > C_V.

2-7. Чайник, содержащий 1 кг кипящей воды, нагревают до полного испарения при нормальном давлении. Определите A, Q, U, H для этого процесса. Мольная теплота испарения воды 40.6 кДж/моль.

2-8. Определите конечную температуру и работу, необходимую для адиабатического сжатия азота от 10 л до 1 л, если начальные температура и давление равны 26.8 о С и 101.3 кПа, соответственно.

2-9. Три моля идеального одноатомного газа (C_V = 3.0 кал/(моль . К)), находящегося при T₁ = 350 K и P₁ = 5 атм, обратимо и адиабатически расширяются до давления P₂ = 1 атм. Рассчитайте конечные температуру и объем, а также совершенную работу и изменение внутренней энергии и энтальпии в этом процессе.

2-10. Система содержит 0.5 моль идеального одноатомного газа (C_V = 3.0 кал/(моль . К)) при P₁ = 10 атм и V₁ = 1 л. Газ расширяется обратимо и адиабатически до давления P₂ = 1 атм. Рассчитайте начальную и конечную температуру, конечный объем, совершенную работу, а также изменение внутренней энергии и энтальпии в этом процессе. Рассчитайте эти величины для соответствующего изотермического процесса.

2-11. Рассчитайте количество теплоты, необходимое для нагревания воздуха в квартире общим объемом 600 м 3 от 20 о С до 25 о С. Примите, что воздух — это идеальный двухатомный газ, а давление при исходной температуре нормальное. Найдите U и H для процесса нагревания воздуха.

2-12. Человеческий организм в среднем выделяет 10 4 кДж в день благодаря метаболическим процессам. Основной механизм потери этой энергии — испарение воды. Какую массу воды должен ежедневно испарять организм для поддержания постоянной температуры? Удельная теплота испарения воды — 2260 Дж/г. На сколько градусов повысилась бы температура тела, если бы организм был изолированной системой? Примите, что средняя масса человека — 65 кг, а теплоемкость равна теплоемкости жидкой воды.

2-13. Один моль паров брома обратимо и изотермически сконденсировали в жидкость при 59 о С. Рассчитайте работу, теплоту, изменение внутренней энергии и энтальпии в этом процессе. Удельная теплота испарения брома при 59 о С равна 184.1 Дж/г.

2-14. Один моль идеального одноатомного газа вступает в следующий замкнутый цикл:

Процесс 1 2 — изотермический, 3 1 — адиабатический. Рассчитайте объемы состояний 2 и 3, а также температуры состояний 1, 2 и 3, считая стадии 1 2 и 3 1 обратимыми. Рассчитайте U и H для каждой стадии.

2-15. Придумайте циклический процесс с идеальным газом, состоящий из четырех стадий. Изобразите этот процесс в координатах p — V. Рассчитайте полное изменение внутренней энергии, а также теплоту и совершенную газом работу.

2-16. Один моль фтороуглерода расширяется обратимо и адиабатически вдвое по объему, при этом температура падает от 298.15 до 248.44 К. Чему равно значение C_V?

2-17. Докажите соотношение (2.16) для работы обратимого адиабатического процесса.

2-18. Один моль метана, взятый при 25 о С и 1 атм, нагрет при постоянном давлении до удвоения объема. Мольная теплоемкость метана дается выражением:

Рассчитайте U и H для этого процесса. Метан можно считать идеальным газом.

2-19. Выведите уравнение для обратимого адиабатического сжатия неидеального газа, если уравнение состояния одного моля газа имеет вид:

2-20*. Используя уравнение состояния и первый закон термодинамики, выведите уравнение адиабаты для газа Ван-дер-Ваальса.

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

II. Молекулярная физика

Видео:Физика. 10 класс. Первое начало термодинамики в применении к изопроцессамСкачать

Тестирование онлайн

Видео:Физика. Термодинамика: Первое начало термодинамики. Центр онлайн-обучения «Фоксфорд»Скачать

Первый закон термодинамики

Первый закон термодинамики — есть закон сохранения энергии: при любых физических взаимодействиях энергия не возникает и не исчезает, а только передается от одних тел другим или превращается из одной формы в другую.

Общая форма закона сохранения и превращения энергии имеет вид

Но изучая тепловые процессы, мы будем рассматривать формулу

Согласно первому закону термодинамики, изменение внутренней энергии термодинамической системы при переходе из одного состояние в другое равно сумме работы, выполненной внешними силами, и количества теплоты, переданной системе извне

Сформулировать первый закон термодинамики можно иначе: количество теплоты, получаемое системой извне при ее переходе из одного состояния в другое, расходуется на повышение внутренней энергии системы и на работу, которую она выполняет против внешних сил

Например, вы кипятите чайник с водой. Количество тепла расходуется на их нагревание (увеличивается энергия частиц, то есть внутренняя энергия системы), а затем происходит приподнимание крышки — это работа, которую выполняет система.

Внешняя работа над системой равна работе системы, но с противоположным знаком

Видео:Первый закон термодинамики. 10 класс.Скачать

Адиабатический (адиабатный) процесс

Процесс при тепловой изоляции системы от окружающей среды, то есть

Изменение внутренней энергии происходит только за счет работы внешних сил. Или совершаемая системой работа происходит за счет убыли внутренней энергии.

Практически все реальные процессы происходят с теплообменом: адиабатические процессы — это редкое исключение.

Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Первый закон термодинамики для изопроцессов

При изотермическом процессе температура не изменяется, значит не изменяется внутренняя энергия

Первый закон принимает вид

Все количество теплоты, которую получает газ расходуется на выполнение им работы против внешних сил. Или, если газ сжимается, при этом не изменяется температура, работу выполняют внешние силы, а газ отдает некоторое количество теплоты в окружающую среду.

При изохорном процессе объем не изменяется, значит работа нулевая

Первый закон термодинамики принимает вид

В этом случае

Если газ изохорно охлаждается, его внутренняя энергия уменьшается, и он отдает теплоту в окружающую среду.

При изобарном процессе первый закон термодинамики имеет общий вид

Здесь справедливы формулы

Видео:Первое начало термодинамики в изопроцессах. Уравнение ПуассонаСкачать

Первое начало термодинамики

Вы будете перенаправлены на Автор24

Закон сохранения энергии для количества теплоты как формы энергии может быть записан в виде:

[delta Q=dU+delta A left(1right).]

[CdT=dU+delta A left(2right),]

где C — теплоемкость системы.

В термодинамике уравнение (1) является крайне важным и называется первым началом. В отличие от закона сохранения их механики, первое начало термодинамики содержит бесконечно малое количество теплоты $delta Q$. Мы знаем, что изучение разного рода переходов именно этой формы энергии — предмет термодинамики. Очень часто уравнение (1) записывается в виде:

[delta Q=dU+pdV left(3right).]

Уравнения (1), (2) и (3) записаны в дифференциальной форме.

В связи с тем, что теплота и работа не являются функциями состояния, то для бесконечно малого количества теплоты и элементарной работы используют обозначение $delta Q$, а не $dQ$ и $delta A$, а не $dA$. Этим подчёркивается, что $delta Q$ и $delta A$ не рассматриваются как полные дифференциалы, т.е. невсегда могут быть представлены как бесконечно малые приращения функций состояния (только в частных случаях).

Первое начало термодинамики не может предсказать направление развития процесса. Этот закон лишь констатирует факт изменения величин в процессе и говорит о величине их изменения. Забегая вперед, скажем, что второе начало термодинамики определяет направление процесса.

В том случае, если рассматривается круговой процесс (система возвращается в исходное состояние), изменение внутренней энергии системы $dU=0$, то первое начало термодинамики говорит о том, что все тепло, которое получила система, идет на совершение этой системой работы.

Видео:Адиабатный процесс. 10 класс.Скачать

Интегральная форма первого начала термодинамики

Первое начало термодинамики можно записать и в интегральной форме:

[Q=triangle U+A left(4right).]

На словах уравнение (4) означает, что подводимая к системе теплота идет на изменение внутренней энергии системы и совершение этой системой работы.

Обратимся опять к круговому процессу ($triangle U$). Если в круговом процессе $Q=0, то A=0.$ Это означает, что невозможен процесс производства работы без какого-то ни было изменения во внешних к системе телах. Или говорят по-другому: не возможен вечный двигатель первого рода.

Рассмотрим изохорный процесс. При постоянном объеме система работу не совершает. В таком случае:

говорят, что все подводимое к системе тепло идет на изменение (увеличение) внутренней энергии системы.

В изотермическом процессе внутренняя энергия системы неизменна, следовательно:

все подводимое системе тепло идет на совершение системой работы.

Задание: В идеальном газе совершается процесс заданный уравнением: $T=T_0e^$, где $T_0, a- $ постоянные. Изохорная молярная теплоемкость газа $c_$ известна. Найти $c_$(V) для заданного процесса.

Основой для решения будет первое начало термодинамики в дифференциальном виде:

[CdT=dU+delta A left(1.1right).]

Приращение внутренней энергии $dU$ равно:

[dU=fracnu RdT to CdT=fracnu RdT +pdVleft(1.2right),]

Используем для дальнейших вычислений уравнение Менделеева — Клайперона:

Подставим в (1.3) вместо T уравнение процесса, получим:

[pV=nu RT_0e^to p=nu RT_0frac<e^> left(1.4right).]

Так как из уравнения процесса $dT$ равно:

То, подставив (1.5) и (1.4) в (1.2), получим выражение:

Соответственно, для молярной теплоемкости процесса получим:

Ответ: Молярная теплоемкость для заданного процесса выражается формулой: $c_left(Vright)=c_+frac$.

Готовые работы на аналогичную тему

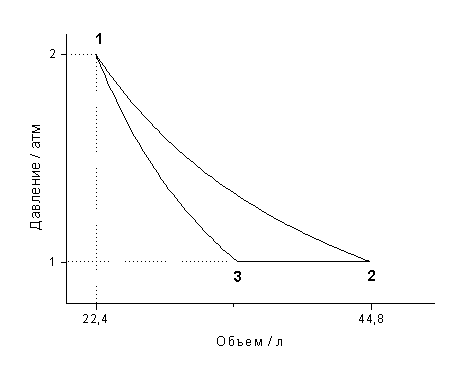
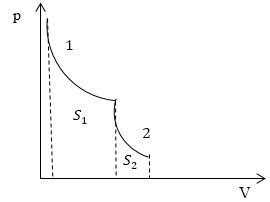
Задание: На рис.1 представлен процесс, состоящий из изотермы (1) и адиабаты (2). Укажите площадь, которая представляет количество теплоты, которое поглощает газ.

Запишем первое начало термодинамики в интегральном виде:

[Q=triangle U+A left(2.1right).]

Первая часть процесса, который представлен на рис.1, является изотермой, следовательно: $triangle U_1=0$ и уравнение (2.1) запишется, как:

Вторая часть процесса представлена адиабатой. Относительно адиабатных процессов известно, что они проводятся без подвода тепла, следовательно:

а работа по расширению газа идет за счет уменьшения его внутренней энергии.

Итак, мы получили, что в указанном на рис.1 процессе тепло подводится только на участке 1, и оно равно работе, которую совершает газ в процессе своего расширения. По определению в процессе 1 работа равна:

Из геометрического свойства интеграла $A_1=S_1$ на рис. 1.

Ответ: Количество теплоты, подведенное в заданном процессе, представлено площадью $S_1$ на рис. 1.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26.11.2021

Видео:2 1 Первый закон термодинамики ЭнтальпияСкачать

Первый закон термодинамики

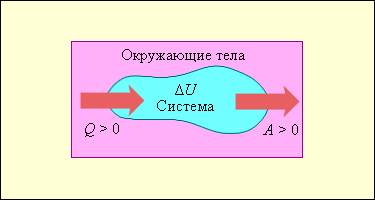
На рисунке 3 . 9 . 1 условно проиллюстрированы энергетические потоки между выделенной термодинамической системой и окружающими телами. В случае, если тепловой поток направлен к термодинамической системе, то некоторая величина Q > 0 , если же система совершает положительную работу над окружающими ее объектами, то справедливо неравенство A > 0 .

Рисунок 3 . 9 . 1 . Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.

Состояние системы меняется, когда происходит процесс ее обмена теплом с окружающими объектами, и она совершает положительную или отрицательную работу. Изменяются макроскопические параметры системы, такие как температура, объем и давление. По причине того, что внутренняя энергия U всецело определяется макроскопическими параметрами, которые характеризуют состояние системы, процессы совершения работы и теплообмена провоцируют изменения внутренней энергии данной системы Δ U .

Видео:Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Определение 1 -го закона термодинамики

Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом:

Изменение Δ U внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q , переданной системе, и работой A , совершенной системой над внешними телами.

Формула первого закона термодинамики, зачастую записывается в ином виде:

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу A над внешними объектами, только получая некоторое количество теплоты Q от окружающих тел или уменьшая Δ U своей внутренней энергии.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Первый закон термодинамики в процессах газов

Первый закон термодинамики может применяться к изопроцессам в газах.

В изохорном процессе, то есть в условиях неизменного объема ( V = c o n s t ) , газ не совершает работы, A = 0 .

В этом случае справедливой будет формула внутренней энергии газа:

Q = ∆ U = U ( T 2 ) — U ( T 1 ) .

В данном выражении U ( T 1 ) и U ( T 2 ) представляют внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит лишь от температуры, что исходит из закона Джоуля. При изохорном нагревании газ поглощает тепло ( Q > 0 ) , чем провоцирует увеличение его внутренней энергии. В условиях охлаждения тепло отдается внешним объектам ( Q 0 ) .

В изобарном процессе, предполагающем постоянность значения давления ( p = c o n s t ) , работа, совершаемая газом, выражается в виде соотношения:

A = p ( V 2 — V 1 ) = p ∆ V .

Первый закон термодинамики для изобарного процесса дает:

Q = U ( T 2 ) — U ( T 1 ) + p ( V 2 — V 1 ) = ∆ U + p ∆ V .

При изобарном расширении Q > 0 тепло поглощается газом, и он совершает положительную работу. При изобарном сжатии Q 0 тепло переходит внешним телам. В таком случае A 0 . При изобарном сжатии уменьшаются температура газа T 2 T 1 и значение внутренней энергии Δ U 0 .

В изотермическом процессе температура газа не меняет своей величины, следовательно, не изменяется и внутренняя энергия газа, Δ U = 0 .

Первый закон термодинамики для изотермического процесса выражается соотношением

Теплота Q , приобретенная газом в процессе изотермического расширения, превращается в работу, совершаемую над внешними объектами. И наоборот, изотермическое сжатие приводит к преобразованию уже работы внешних сил, произведенной над газом, в передающееся окружающим телам тепло.

Вместе с изохорным, изотермическим и изобарным процессами в термодинамике нередко исследуют процессы, происходящие в условиях отсутствующего теплообмена с окружающими объектами.

Адиабатическая оболочка – это сосуд с теплонепроницаемыми стенками.

Процессы сжатия или расширения газа в подобных емкостях называют адиабатическими.

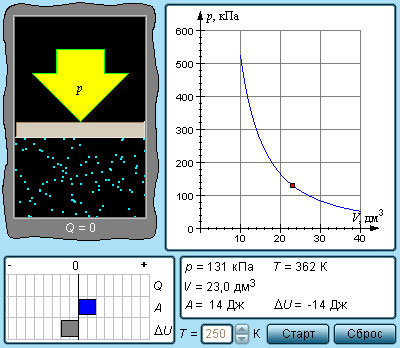
Рисунок 3 . 9 . 2 . Модель адиабатического процесса.

В адиабатическом процессе Q = 0 . По данной причине первый закон термодинамики принимает вид:

Выходит, что газ производит работу за счет падения значения его внутренней энергии.

Расширение или сжатие газа на плоскости p , V проиллюстрирована кривой, называемой адиабатой.

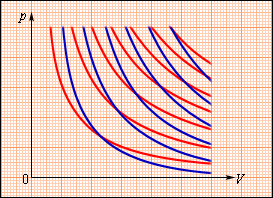
В процессе адиабатического расширения газом совершается положительная работа A > 0 , что является причиной понижения значения внутренней энергии Δ U 0 . Данное явление провоцирует падение его температуры. Исходя из этого, можно заявить, что величина давления газа при адиабатическом расширении понижается быстрее, чем это происходит в изотермическом (рис. 3 . 9 . 3 ).

Рисунок 3 . 9 . 3 . Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа.

В условиях координат ( p , V ) выводящееся в термодинамике уравнение адиабатического процесса для идеального газа принимает следующий вид:

p V γ = c o n s t .

Данное выражение, в котором γ = C p C V – показатель адиабаты, C p и C V – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом, называется уравнением Пуассона. В условиях одноатомного газа γ = 5 3 = 1 , 67 , двухатомного γ = 7 5 = 1 , 4 , многоатомного γ = 1 , 33 .

Работа газа в адиабатическом процессе выражается через температуры начального T 1 и конечного T 2 состояний и принимает вид:

A = C V ( T 2 — T 1 )

Адиабатический процесс относится к изопроцессам.

В термодинамике важное место занимает физическая величина, называемая энтропией. Изменение энтропии в том или ином квазистатическом процессе эквивалентно некоторому обретенному системой теплу Δ Q T . Так как на каждом участке адиабатического процесса Δ Q = 0 , энтропия в нем не претерпевает изменений.

Любые изопроцессы, в том числе и адиабатические, являются квазистатическими. Промежуточные состояния газа в таких процессах близки к состояниям термодинамического равновесия. Каждая точка, принадлежащая адиабате, описывает равновесное состояние. Однако, процесс, который проводится в адиабатической оболочке, то есть при отсутствующем теплообмене с окружающими объектами, не обязательно удовлетворяет данному условию.

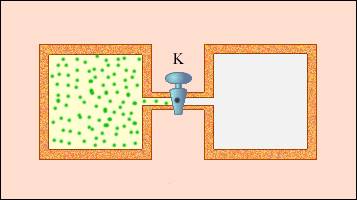
Примером неквазистатического процесса, в котором промежуточные состояния не находятся в состоянии равновесия, служит расширение газа в пустоту. На рисунке 3 . 9 . 3 иллюстрируется жесткая адиабатическая оболочка, состоящая из двух разделенных вентилем K сообщающихся емкостей. В изначальном состоянии газом заполнен один из сосудов, в это же время во втором находится лишь вакуум. Открытие вентиля запускает процесс расширения газа. Он заполняет оба сосуда, и устанавливается новое равновесное состояние.

В таком процессе Q = 0 , по той причине, что исключен теплообмен с окружающими телами, и A = 0 , так как оболочка недеформируема. Первый закон термодинамики позволяет сказать, что Δ U = 0 , то есть внутренняя энергия газа не претерпела никаких изменений. Так как внутренняя энергия идеального газа зависит лишь от температуры, температура газа в начальном и конечном состояниях одинакова. Изображающие эти состояния точки на плоскости ( p , V ) лежат на одной изотерме. Все промежуточные состояния газа не являются равновесными и не могут быть изображены на диаграмме.

Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.

Рисунок 3 . 9 . 4 . Расширение газа в пустоту.

🔥 Видео

Что такое первый закон термодинамики?Скачать

Первое начало термодинамики. Изопроцессы.Скачать

Физика 10 класс (Урок№24 - Первый закон термодинамики.)Скачать

Решение задач на первое начало термодинамики. ТермохимияСкачать

Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Урок 9. Термодинамика. Первое начало термодинамики. Циклы. КПД.Скачать

Применение первого начала термодинамики к изопроцессамСкачать

ЧК_МИФ ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИСкачать

Физика. 10 класс. Первое начало термодинамикиСкачать

Лекция 08 Первое начало термодинамикиСкачать