Перевод уравнения в функцию эксель

Если в ячейку Excel введена формула, содержащая ссылку на эту же самую ячейку (может быть и не напрямую, а опосредованно — через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). На практике к циклическим ссылкам прибегают, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя ее устранения. Excel не может провести вычисления, так как циклические ссылки порождают бесконечное количество вычислений. Есть два выхода из этой ситуации: устранить циклические ссылки или допустить вычисления по формулам с циклическими ссылками (в последнем случае число повторений цикла должно быть конечным).

Рассмотрим задачу нахождения корня уравнения методом Ньютона с использованием циклических ссылок. Возьмем для примера квадратное уравнение: х 2 — 5х + 6=0, графическое представление которого приведено на рис. 8. Найти корень этого (и любого другого) уравнения можно, используя всего одну ячейку Excel.

Для включения режима циклических вычислений в меню Сервис/Параметры/вкладка Вычисления включаем флажок Итерации, при необходимости изменяем число повторений цикла в поле Предельное число итераций и точность вычислений в поле Относительная погрешность (по умолчанию их значения равны 100 и 0,0001 соответственно). Кроме этих установок выбираем вариант ведения вычислений: автоматически или вручную. При автоматическом вычислении Excel выдает сразу конечный результат, при вычислениях, производимых вручную, можно наблюдать результат каждой итерации.

Рис. 8. График функции

Выберем произвольную ячейку, присвоим ей новое имя, скажем — Х, и введем в нее рекуррентную формулу, задающую вычисления по методу Ньютона:

где F и F1 задают соответственно выражения для вычисления значений функции и ее производной. Для нашего квадратного уравнения после ввода формулы в ячейке появится значение 2, соответствующее одному из корней уравнения (рис. 8). В нашем случае начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке Х и равного нулю. А как получить второй корень? Обычно это можно сделать изменением начального приближения. Решать проблему задания начальных установок в каждом случае можно по-разному. Мы продемонстрируем один прием, основанный на использовании функции ЕСЛИ. С целью повышения наглядности вычислений ячейкам были присвоены содержательные имена (рис. 9).

• В ячейку Хнач (В4) заносим начальное приближение — 5.
• В ячейку Хтекущ (С4) записываем формулу:
  =ЕСЛИ(Хтекущ=0;Хнач; Хтекущ-(Хтекущ^2-5*Хтекущ+6)/(2*Хтекущ-5)).
• В ячейку D4 помещаем формулу, задающую вычисление значения функции в точке Хтекущ, что позволит следить за процессом решения.
• Заметьте, что на первом шаге вычислений в ячейку Хтекущ будет помещено начальное значение, а затем уже начнется счет по формуле на последующих шагах.
• Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Хнач и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного
  

  Рис. 9. Определение начальных установок

  значения. Чтобы обнулить значение, хранящееся в ячейке Хтекущ, нужно заново записать туда формулу. Для этого достаточно для редактирования выбрать ячейку, содержащую формулу, дважды щелкнув мышью на ней (при этом содержимое ячейки отобразится в строке формул). Щелчок по кнопке (нажатие клавиши) Enter запустит вычисления с новым начальным приближением.

2.2. Подбор параметра

Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

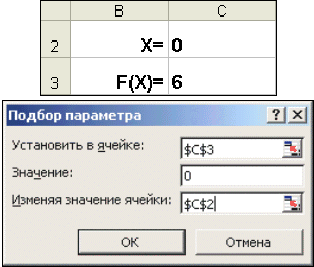
Возьмем в качестве примера все то же квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:

• В ячейку С3 (рис. 10) введем формулу для вычисления значения функции,
  

  Рис. 10. Окно диалога Подбор параметра

  стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.

• В окне диалога Подбор параметра (рис. 10) в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
• После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.

Вернемся к примеру. Опять возникает вопрос: как получить второй корень? Как и в предыдущем случае необходимо задать начальное приближение. Это можно сделать следующим образом (рис. 11,а):

а

б

Рис. 11. Поиск второго корня

• В ячейку Х (С2) вводим начальное приближение.
• В ячейку Х_i (С3) вводим формулу для вычисления очередного приближения к корню, т.е.
  =X-(X^2-5*X+6)/(2*X-5).
• В ячейку С4 поместим формулу, задающую вычисление значения функции, стоящей в левой части исходного уравнения, в точке Х_i.
• После этого выбираем команду Подбор параметра, где в качестве изменяемой ячейки принимаем ячейку С2. Результат вычислений изображен на рис. 11,б (в ячейке С2 — конечное значение, а в ячейке С3 — предыдущее).

Однако все это можно сделать и несколько проще. Для того чтобы найти второй корень, достаточно в качестве начального приближения (рис. 10) в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.

2.3. Поиск решения

Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.

Задачи, которые можно решать с помощью Поиска решения, в общей постановке формулируются так:

Искомые переменные — ячейки рабочего листа Excel — называются регулируемыми ячейками. Целевая функция F(х₁, х₂, … , х_n), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:

• найти максимум целевой функции F(х₁, х₂, … , х_n);
• найти минимум целевой функции F(х₁, х₂, … , х_n);
• добиться того, чтобы целевая функция F(х₁, х₂, … , х_n) имела фиксированное значение: F(х₁, х₂, … , х_n) = a.

Функции G(х₁, х₂, … , х_n) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.

Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решать. И тогда для решения конкретной оптимизационной задачи требуется специально для нее сконструированный метод. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ.

Выше для нахождения корней квадратного уравнения был применен метод Ньютона (п. 1.4) с использованием циклических ссылок (п. 2.1) и средство Подбор параметра (п. 2.2). Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.

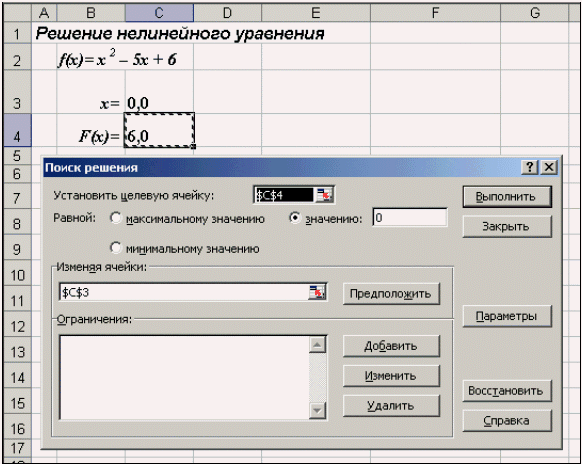Рис. 12. Окно диалога Поиск решения

После открытия диалога Поиск решения (рис. 12) необходимо выполнить следующие действия:

1. в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
2. для максимизации значения целевой ячейки, установить переключатель максимальному значению в положение 8 , для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
3. в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
4. в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
5. для запуска процесса поиска решения нажать кнопку Выполнить.

Рис. 13. Результаты поиска

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.

Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения), следующие (рис. 14):

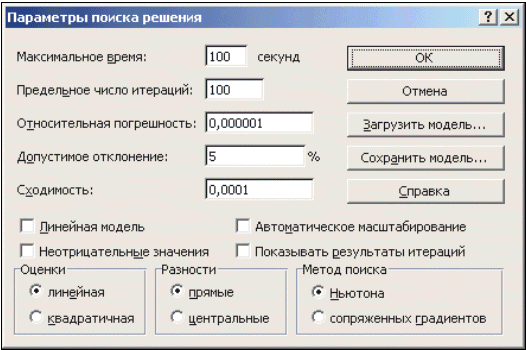Рис. 14. Настройка параметров Решателя

• Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).
• Предельное число итераций — еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, и, чаще всего, если решение не получено за 100 итераций, то при увеличении их количества (в поле можно ввести время, не превышающее 32767 секунд) вероятность получить результат мала. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.
• Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).
• Допустимое отклонение — задается в % только для задач с целочисленными ограничениями. Поиск решения в таких задачах сначала находит оптимальное нецелочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более, чем на указанное данным параметром количество процентов.
• Сходимость — когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа (дробь из интервала от 0 до 1), указанного в данном параметре, поиск прекращается.
• Линейная модель — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Это ускоряет процесс поиска решения.
• Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.
• Автоматическое масштабирование — этот флажок следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, определяющая максимальную прибыль, измеряется в миллиардах рублей.
• Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.
• Оценки — эта группа служит для указания метода экстраполяции — линейная или квадратичная, — используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Линейная служит для использования линейной экстраполяции вдоль касательного вектора. Квадратичная служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.
• Разности (производные) — эта группа служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций. Параметр Прямые используется в большинстве задач, где скорость изменения ограничений относительно невысока. Параметр Центральные используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается.
• Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.

Сохранить модель поиска решения можно следующими способами:

1. при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;
2. если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например найти максимум и минимум одной функции, или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Параметры/Сохранить модель окна Поиск решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Параметры/Загрузить модель диалога Поиск решения;
3. еще один способ сохранения параметров поиска — сохранение их в виде именованных сценариев. Для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений.

Кроме вставки оптимальных значений в изменяемые ячейки Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения. Рассмотрим более подробно каждый из них.

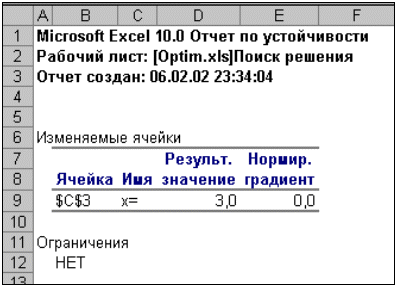Рис. 15. Отчет по устойчивости

Отчет по устойчивости (рис.15) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. Раздел для изменяемых ячеек содержит значение нормированного градиента, которое показывает, как целая ячейка реагирует на увеличение значения в соответствующей изменяемой ячейке на одну единицу. Подобным образом, множитель Лагранжа в разделе для ограничений показывает, как целевая ячейка реагирует на увеличение соответствующего значения ограничения на одну единицу. При использовании целочисленных ограничений Excel выводит сообщение Отчеты устойчивость и Пределы не применимы для задач с целочисленными ограничениями. Если в окне диалога Параметры поиска решения установлен флажок Линейная модель, то отчет по устойчивости содержит несколько дополнительных столбцов информации.

Рис. 16. Отчет по результатам

Отчет по результатам (рис.16) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй — значения искомых переменных, полученные в результате решения задачи, в третьей — результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы — это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение — это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение — это ограничение, которое было выполнено с ненулевым значением разницы.

Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:решаем квадратные уравнения в ExcelСкачать

Переводчик функций в Excel

В этой статье вы настроили и использовали надстройки Excel Переводчик функций. Функция Переводчик ориентирована на людей, которые используют версии Excel на разных языках, и требуют помощи в поиске нужной функции на нужном языке или даже переводе целых формул с одного языка на другой.

Помогает пользователям, знакомым с английскими функциями Excel, продуктивно работать с локализованными версиями Excel.

Позволяет пользователям полностью переводить формулы на родной язык.

Поддерживает все локализованные языки и функции Excel (80 языков и 800 функций).

Обеспечивает эффективный поиск любой части имени функции на обоих выбранных языках.

Отображает прокручиваемый список по категориям для английских функций и соответствующие локализованные функции.

Позволяет отправить корпорации Майкрософт отзыв о качестве перевода функций. Вы можете оставить отзыв о той или иной функции на любом из доступных языков.

Локализован на английский, датский, немецкий, испанский, французский, итальянский, японский, корейский, нидерландский, португальский (Бразилия), русский, шведский, турецкий и китайский (традиционное письмо и набор сложных знаков) языки.

Видео:Решение системы уравнений в ExcelСкачать

Установка надстройки «Переводчик функций»

Надстройка Переводчик функций доступна бесплатно в Microsoft Store. Чтобы установить ее, выполните указанные ниже действия.

Запустите приложение Microsoft Excel.

Перейдите на вкладку Вставка.

Нажмите кнопку Магазин на ленте.

Откроется диалоговое окно «Надстройки Office». В верхней части окна выберите пункт Магазин, а слева — Производительность.

Введите в поле поиска запрос Functions Translator.

Нажмите зеленую кнопку Добавить справа от найденной надстройки «Переводчик функций». Она будет установлена.

Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Настройка Переводчика функций

После установки надстройки Переводчик функций на вкладке Главная справа появятся две новых кнопки.

Они открывают в диалоговом окне Переводчик функций области Справочник и Переводчик соответственно. Исключением является первый запуск надстройки Переводчик функций — в этом случае открывается область Добро пожаловать:

Рабочая область Переводчика функций всегда открывается в правой части Excel.

Вы можете перейти непосредственно к переводу, щелкнув ссылку Пропустить > в правом верхнем углу, но мы рекомендуем нажать кнопку Приступим, чтобы перейти в диалоговое окно языковых параметров. Здесь вы можете выбрать языки С и На по умолчанию (их можно изменить в любое время).

Здесь вы можете указать языковые параметры. Хотя Переводчик функций поддерживает все языки, на которые локализованы функции Excel, в каждом случае вы можете использовать только пару из них. Доступно любое сочетание языков, и приложение Excel запомнит ваш выбор. Вы в любое время можете изменить языковую пару в области Настройки, которую можно открыть во всех основных областях Переводчика функций.

По умолчанию в качестве языка «С» и «На» будут заранее заполнены английский язык с языком «От», а языком установки Excel языком «На». Если язык установки является одним из языков, локализованных для Переводчик,пользовательский интерфейс будет отображаться на локализованных языках. Выберите языковую пару, нажав кнопку Начать работу.

В переводчике используются параметры С и На. С — это язык, который вы знаете, На — это язык, перевод на который вам нужен. Так, если вы используете для поиска функций английский язык, но хотите найти их имена на французском языке, то для параметра С нужно выбрать английский язык, а для параметра На — французский.

С помощью зеленой кнопки Стрелка вверх/стрелка вниз между параметрами «С» и «На» можно менять языки С и На местами.

Вы можете открыть область Настройки, щелкнув значок настроек в правом нижнем углу любой из трех основных областей.

Кроме того, вы можете в любое время изменить языки На и От, которые могут быть вам интересны. Если щелкнуть стрелку влево в верхней части области, вы вернетсяе в главную.

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

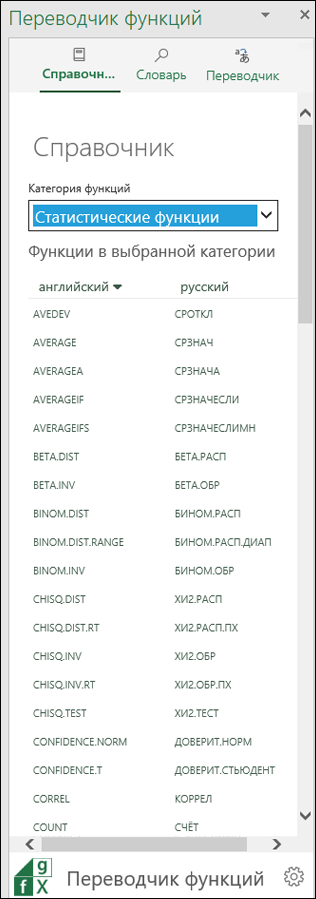
Область «Справочник»

В области Справочник есть раскрывающийся список Категория функций, с помощью которого можно отобразить все функции в указанной категории для языков С (слева) и На (справа). Если вы не знаете, к какой категории относится функция, можно использовать параметр Все.

По умолчанию функции сортируются в алфавитном порядке языка С (в данном случае английского), рядом с которым отображается маленькая стрелка вниз. Вы можете сортировать функции в обычном или обратном алфавитном порядке, а также выбирать язык сортировки ( С или На). Просто щелкните название языка, по которому нужно отсортировать функции, а для сортировки в обратном порядке щелкните его еще раз. Стрелка указывает направление сортировки.

Щелкните имя функции в одном из столбцов, чтобы открыть область Словарь с кратким описанием функции.

Видео:Перевод в ExcelСкачать

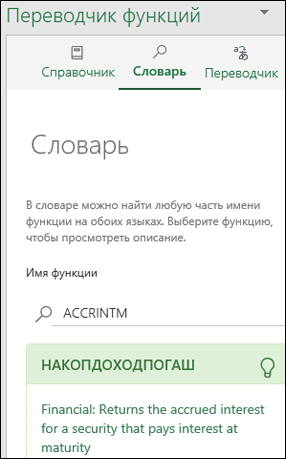
Область «Словарь»

В области Словарь можно искать любые части имени функции, отображая все функции, содержащие введенные буквы. По соображениям производительности поиск не будет заполнять результаты, пока вы не ввели хотя бы две буквы. Поиск будет искаться в выбранной языковой паре и возвращать результаты для обоих языков.

Обнаружив нужное имя функции, вы можете щелкнуть его, чтобы отобразить языковую пару и определение функции. Если щелкнуть имя функции в области Справочник, также откроется область Словарь с указанием языковой пары и описания функции.

У некоторых функций нет описаний.

Описания функций предоставляются только на английском языке.

Чтобы посмотреть локализованное описание, перейдите на вкладку «Формулы», щелкните нужную категорию функций и наведите указатель мыши на требуемую функцию. В Excel отобразится описание функции на языке установки.

Щелкните значок лампочки в области Словарь, чтобы открыть область Отзыв о переводе, где вы можете оставить отзыв об определенном переводе.

Видео:MS Excel - Ввод формулСкачать

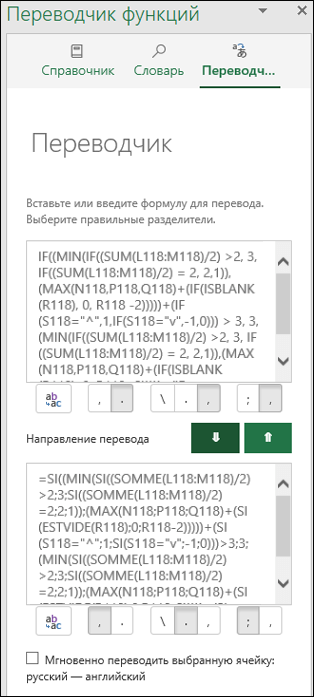
Область «Переводчик»

В области Переводчик можно полностью перевести формулу с одного языка на другой. Ниже приведен пример области Переводчик, где формула переведена с английского языка на французский:

Верхнее поле предназначено для языка С, нижнее — для языка На. Две зеленые кнопки со стрелками между этими полями выполняют перевод в указанном направлении. В примере мы вставили формулу в поле для языка С и нажали кнопку со стрелкой вниз, чтобы перевести формулу на французский язык.

Ручная настройка разделителей

В функциях Excel для разделения диапазонов и аргументов используются разделители. В каждом языке используются свои разделители, и Переводчик функций пытается подобрать нужный вариант, но иногда разделители следует выбирать вручную.

Под полями для языков «С» и «На» отображаются показанные выше кнопки. Первая кнопка вставляет текст из поля выше в активную ячейку. Эту кнопку можно использовать для вставки локализованной формулы в нужную ячейку.

Остальные кнопки распределены по соответствующим функциям: десятичный разделитель, разделитель столбцов для формул массива и разделитель элементов списка.

Десятичным разделителем может быть точка или запятая.

Разделитель столбцов для формул массива

Этот разделитель используется в формулах массива.

Разделитель элементов списка

С английским языком в качестве десятичного разделителя обычно используется точка, а в качестве разделителя элементов списка — запятая. В некоторых европейских языках десятичным разделителем является запятая, а разделителем элементов списка другой символ, а именно точка с запятой.

Мгновенно переводить выбранную ячейку

Если установлен флажок Мгновенно переводить выбранную ячейку в области Переводчик, надстройка будет пытаться перевести формулу в любой выбираемой ячейке. Она будет копировать формулу из выбранной ячейки в поле языка На и мгновенно переводить ее в поле языка С.

Функция Мгновенно переводить выбранную ячейку не поддерживается в Microsoft Excel 2013 и более ранних версий.

В режиме правки функция  Мгновенно переводить выбранную ячейку не активна. При выходе из режима правки функция мгновенного перевода активируется снова.

Видео:23 Функция ЕСЛИ в Excel (IF)Скачать

Отзывы и предложения

Мы надеемся, что надстройка Переводчик функций поможет вам эффективнее работать с локализованными версиями Excel, и будем рады вашим отзывам. Сообщите нам о функциях, перевод которых можно улучшить, и поделитесь мнением о работе самой надстройки.

Если у вас есть предложения по поводу улучшения работы надстройки и локализации функций в общем, обязательно отправьте их нам!

Команда Переводчика функций, Мартин и Вадим

Примечание: Мы рассмотрим каждый отзыв индивидуально, но не можем гарантировать ответ на каждый отзыв. Не включайте в отзыв файлы, содержащие личные сведения.

Видео:Урок 4. Формулы Excel для начинающихСкачать

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Видео:Математика это не ИсламСкачать

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Видео:Табулирование функции и построение графика в ExcelСкачать

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

2. Переходите к инструменту и заполняете все необходимые поля

3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Видео:12 Функция Excel ЧАСТОТАСкачать

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Видео:Секреты работы с текстом в Эксель ➤ Функции Excel: СЦЕПИТЬ, СЦЕП и ОБЪЕДИНИТЬСкачать

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Видео:Вычисление оценок, комиссий и т.д. в Excel - ВПР и ИСТИНА - Функции Excel (11)Скачать

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

💡 Видео

Решение уравнений с помощью ExcelСкачать

Парная регрессия: линейная зависимостьСкачать

Как найти обратную матрицу в экселеСкачать

Нахождение предела функции в MS ExcelСкачать

Квадратное уравнение в ExcelСкачать

Поиск решения в ExcelСкачать

Быстрое построение графика функции в EXCELСкачать