Перевести уравнение плоскости из общего в каноническое

Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Уравнение плоскости в отрезках

В данной статье мы рассмотрим уравнение плоскости в отрезках. Представим методы преобразования уравнения плоскости в отрезках в уравнение плоскости в общем виде и обратно. Рассмотрим численные примеры.

Уравнение плоскости в отрезках представляется следующей формулой:

,

(1)

где a, b, c отличные от нуля числа.

Отметим, что числа a, b, c в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает плоскость на осях Ox, Oy, Oz (Рис.1, Рис.2).

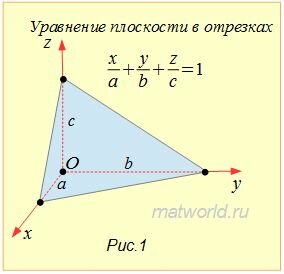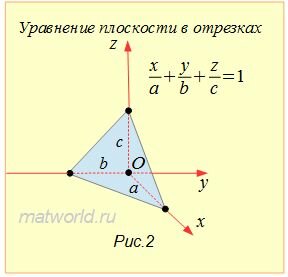Действительно. Подставляя в (1) y=0, z=0 получим x=a, если же подставить в (1) x=0, y=0 то получим z=c, подставвляя, наконец, x=0, z=0 получим y=b. Таким образом плоскость, определяемая уравнением (1) проходит через точки M₁(a, 0, 0), M₂(0, b, 0) и M₃(0, 0, с).

Пример 1. Составить уравнение прямой, которая пересекает оси Ox, Oy и Oz в точках −1,3 и 7, соответственно.

Решение. Подставляя значения a=−1, b=3 и c=7 в (1), получим:

.

.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

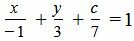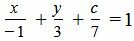Приведение уравнения плоскости в отрезках к общему виду

Левая часть уравнения (1) приведем к общему знаменателю:

.

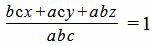Далее, умножив обе части уравнения на abc, получим:

.

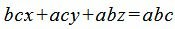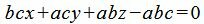Пример 2. Уравнение плоскости в отрезках представлено следующим уравнением:

.

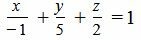Перевести уравнение к общему виду.

Решение. Приведем левую часть уравнения к общему знаменателю:

.

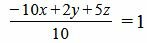Умножив обе части уравнения на 10, получим:

.

.

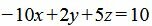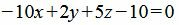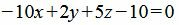Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

где A, B, C, D − отличные от нуля числа, т.е. уравнение плокости является полным (о полных и неполных уравнениях плоскости смотрите здесь).

Сделаем следующие преобразования. Переведем свободный член D на правую часть уравнения и разделим обе части уравнения на −D:

.

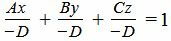(2)

Уравнение (2) можно переписать в следующем виде:

.

(3)

Сделаем следующие обозначения:

Тогда получим уравнение прямой в отрезках (1).

Пример 3. Привести общее уравнение прямой

к уравнению прямой в отрезках.

Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение плоскости в отрезках. Воспользуемся формулой (3). Имеем: A=−2, B=3, C=5, D=−4. Подставив эти значения в формулу (3), получим:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Нахождение уравнений прямой, заданной пересечением двух плоскостей

Этот онлайн калькулятор находит уравнения прямой, заданной пересечением двух плоскостей в пространстве.

Этот онлайн калькулятор предназначен для проверки решений задач, которые можно сформулировать следующим образом:

Записать канонические уравнения прямой, заданной уравнениями двух плоскостей

Вы задаете коэффициенты уравнений плоскостей, калькулятор выдает уравнения прямой в канонической форме. Немного теории, как обычно, можно почерпнуть под калькулятором

Нахождение уравнений прямой, заданной пересечением двух плоскостей

Канонические уравнения прямой, заданной пересечением двух плоскостей

Если плоскости пересекаются, то система уравнений, приведенная в начале статьи, задает прямую в пространстве. Для записи уравнений этой прямой в каноническом виде, надо найти какую либо точку, принадлежащую этой прямой, и направляющий вектор.

Точка, принадлежащая прямой, также принадлежит и каждой из плоскостей, то есть является одним из решений системы уравнений выше. Для нахождения точки, принадлежащей прямой, переходят от системы из двух уравнений с тремя неизвестными к системе из двух уравнений с двумя неизвестными, произвольно принимая какую-либо координату точки за ноль. Как правило, при решении задач, выбирают ту координату, при занулении которой решение системы из двух уравнений с двумя неизвестными дает в ответе целые числа. Калькулятор учитывает этот факт и также пытается найти целочисленное решение, зануляя все координаты по очереди.

Направляющий вектор прямой ортогонален нормальным векторам плоскостей, которые задаются коэффициентами A, B и С в общем уравнении плоскости . Таким образом его можно найти как результат векторного произведения нормальных векторов плоскостей .

Точка и вектор дают нам канонические уравнения прямой:

Существуют частные случаи, когда одна или две координаты направляющего вектора равны нулю.

В случае, если нулю равны две координаты, направляющий вектор коллинеарен одной из координатных осей. Соответственно, точки прямой могут принимать любое значение по этой оси, при этом значения по двум другим осям будут постоянны. Например, если двумя нулевыми координатами будут y и z, канонические уравнения прямой будут выглядеть так:

В случае. если нулю равна одна координата, направляющий вектор лежит в одной из координатных плоскостей (плоскостей, образованных парами координатных осей), значение координаты по третьей оси, ортогональной этой плоскости (как раз той, для которой координата направляющего вектора равна нулю), опять будет постоянным. Например, если нулевой координатой будет x, то канонические уравнения прямой будут выглядеть так:

Эти случаи также учитываются калькулятором.

Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Перевести уравнение плоскости из общего в каноническое

Пусть в декартовой системе координат дан вектор n = и точка М 0 =( x 0 , y 0 , z 0 ).

Построим плоскость Π, проходящую через т. М 0 , перпендикулярную вектору n (этот вектор называют нормальным вектором или нормалью плоскости).

Утверждение 1: М Π ó М 0 М n .

М 0 М= n ó A( x-x 0 )+B( y-y 0 )+C( z-z 0 )=0. (*)

Каноническое уравнение плоскости в пространстве:

Аx+By+Cz+D=0, где D = -A x 0 -B y 0 -C z 0 .

Замечание 1: формула (*) используется при непосредственном решении задач, после упрощения получается искомое каноническое уравнение плоскости.

Пример 1. Написать каноническое уравнение плоскости, перпендикулярной вектору n= и проходящей через точку М(2,-1,1).

Пример 2. Написать каноническое уравнение плоскости, содержащей точки K(2,1,-2), L(0,0,-1), M(1,8,1).

Пусть в декартовой системе координат дан вектор a =

и точка М 0 =( x 0 , y 0 , z 0 ).

Построим прямую l , проходящую через т. М 0 , параллельную вектору a (этот вектор называют направляющим вектором прямой).

Утверждение 2: М l ó М 0 М || a .

М 0 М= || a ó t R , т.ч. М 0 М=t ·a =>

Параметрические уравнения прямой в пространстве:

(**)

Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.

В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t 0 =0 он находится в точке М 0 , в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).

Теперь несколько преобразуем формулы (**).

Выразим из каждой строчки параметр t:

Канонические уравнения прямой в пространстве:

Замечание 2: Эта компактная запись на самом деле содержит три уравнения.

Замечание 3: Это формальная запись и выражение вида в данном случае допустимо.

Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.

Пример 3. Написать канонические и параметрические уравнения прямой, параллельной заданной прямой и проходящей через заданную точку.

Пример 4. Написать канонические уравнения прямой, заданной пересечением двух плоскостей.

Пример 5. Найти точку пересечения прямой и плоскости.

Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М 1 =(x 1 ,y 1 ,z 1 ).

Утверждение 3: расстояние от точки М 1 до плоскости Π вычисляется по формуле:

Пример 6. Найти расстояние от точки до плоскости.

Пусть в декартовой системе координат М 1 =(x 1 ,y 1 ,z 1 ), М 2 =(x 2 ,y 2 ,z 2 ) .

Утверждение 4: Координаты т. М, т.ч. М 1 М=λ∙ММ 2 , находятся по следующим формулам:

.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

🔍 Видео

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Уравнение плоскости. 11 класс.Скачать

Видеоурок "Уравнение плоскости в отрезках"Скачать

5. Нормальное уравнение плоскости выводСкачать

11. Прямая в пространстве и ее уравненияСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

Видеоурок "Общее уравнение плоскости"Скачать

2. Уравнение плоскости примеры решения задач #1Скачать

Видеоурок "Параметрические уравнения прямой"Скачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать