Построим график функции в полярных координатах r=r(φ),
где 0 Выражения могут состоять из функций (обозначения даны в алфавитном порядке): absolute(x) Абсолютное значение x
(модуль x или |x|) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x exp(x) Функция — экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) sin(x) Функция — Синус от x cos(x) Функция — Косинус от x sinh(x) Функция — Синус гиперболический от x cosh(x) Функция — Косинус гиперболический от x sqrt(x) Функция — квадратный корень из x sqr(x) или x^2 Функция — Квадрат x ctg(x) Функция — Котангенс от x arcctg(x) Функция — Арккотангенс от x arcctgh(x) Функция — Гиперболический арккотангенс от x tg(x) Функция — Тангенс от x tgh(x) Функция — Тангенс гиперболический от x cbrt(x) Функция — кубический корень из x gamma(x) Гамма-функция LambertW(x) Функция Ламберта x! или factorial(x) Факториал от x DiracDelta(x) Дельта-функция Дирака Heaviside(x) Функция Хевисайда Интегральные функции: Si(x) Интегральный синус от x Ci(x) Интегральный косинус от x Shi(x) Интегральный гиперболический синус от x Chi(x) Интегральный гиперболический косинус от x
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
© Контрольная работа РУ — калькуляторы онлайн
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Прямоугольная и полярная система координат на плоскости
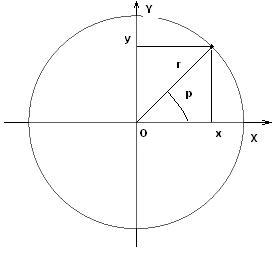
Прямоугольная система координат на плоскости вводится следующим образом. Возьмем на плоскости две взаимно перпендикулярные числовые оси 0х и 0у, имеющие общее начало точку 0 и общую единицу масштаба.
Оси 0х и 0у образуют прямоугольную (декартовую) систему координат на плоскости.
Проекции точки на плоскости на оси координат, а точнее, их числовые значения, называются прямоугольными или декартовыми прямоугольными координатами точки на плоскости.
Кроме прямоугольных декартовых координат на плоскости существуют другие системы координат, позволяющие определить положение каждой точки плоскости с помощью двух действительных чисел. Наиболее употребительной после декартовой системы координат является полярная система координат.
Возьмем на плоскости точку 0, которую назовем полюсом. Проведем из полюса луч 0р, называемый полярной осью.
Полюс и полярная ось образуют полярную систему координат на плоскости.
Расстояние r от точки до полюса называют полярным радиусом точки . Угол между полярной осью и радиусом называют полярным углом точки.
Полярный радиус и полярный угол называют полярными координатами точки на плоскости.
Два калькулятора ниже используются для перехода от прямоугольных координат точки на плоскости к полярным и обратно.
(В предположении, что начала координат у обоих систем совпадают, а полярная ось направлена вдоль положительного направления оси Х)
Видео:Построение кривой в полярной системе координатСкачать

Построить график в полярных координатах на плоскости
Данный калькулятор поможет построить график и кривые на плоскости в полярных координатах.
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.
Полярная система координат задаётся лучом, который называют нулевым лучом, или полярной осью. Точка, из которой выходит этот луч, называется началом координат, или полюсом.
Примеры уравнений кривых в полярных координатах:
R=2*(1-cos theta) — кардиоида;
R=2*sin(4*theta) — полярная роза;
R=2+sin(3* theta) — трохоида;
R=9/(4-5*cos theta) — гипербола.
🎦 Видео
Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Видеоурок "Полярная система координат"Скачать

Полярная система координатСкачать

A.6.6 Переход между декартовой и другими системами координатСкачать

Полярные в декартовыеСкачать

Полярная система координатСкачать

§30 Уравнения кривых второго порядка в полярных координатахСкачать

Занятие 01. Часть 3. Полярная система координатСкачать

Полярная система координат.Скачать

§52 Полярная система координатСкачать

Видеоурок "Преобразование координат"Скачать

Криволинейные системы координат | полярные координаты | координатные кривыеСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Двойной интеграл в полярных координатахСкачать

§53 Связь между полярными и декартовыми координатамиСкачать

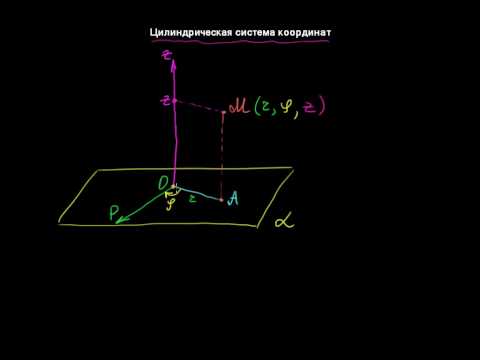
§55 Цилиндрическая система координатСкачать
Скорость и ускорение точки в полярных координатахСкачать