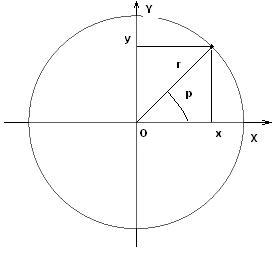
Прямоугольная система координат на плоскости вводится следующим образом. Возьмем на плоскости две взаимно перпендикулярные числовые оси 0х и 0у, имеющие общее начало точку 0 и общую единицу масштаба.
Оси 0х и 0у образуют прямоугольную (декартовую) систему координат на плоскости.
Проекции точки на плоскости на оси координат, а точнее, их числовые значения, называются прямоугольными или декартовыми прямоугольными координатами точки на плоскости.
Кроме прямоугольных декартовых координат на плоскости существуют другие системы координат, позволяющие определить положение каждой точки плоскости с помощью двух действительных чисел. Наиболее употребительной после декартовой системы координат является полярная система координат.
Возьмем на плоскости точку 0, которую назовем полюсом. Проведем из полюса луч 0р, называемый полярной осью.
Полюс и полярная ось образуют полярную систему координат на плоскости.
Расстояние r от точки до полюса называют полярным радиусом точки . Угол между полярной осью и радиусом называют полярным углом точки.
Полярный радиус и полярный угол называют полярными координатами точки на плоскости.
Два калькулятора ниже используются для перехода от прямоугольных координат точки на плоскости к полярным и обратно.
(В предположении, что начала координат у обоих систем совпадают, а полярная ось направлена вдоль положительного направления оси Х)
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Переход от полярного уравнения к декартовому
Неверно введено число.
Полярная система координат
| x | = |
| y | = |
| ρ | = |
| φ | = |
Количество знаков после разделителя дроби в числах:
| ρ | = |
| φ | = |
| x | = |
| y | = |
Теория
Выражение декартовых прямоугольных координат через полярные:
Выражение полярных координат через декартовы прямоугольные :
Видео:Полярная система координатСкачать

Полярная система координат: основные понятия и примеры
Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Полярная система координат: основные понятия и обозначения
Если уж речь зашла о полярной системе координат, то вообразите себя полярниками, стоящими на Северном полюсе. Или на Южном (это не так важно). Пусть в точке полюса находится начало линейки. В точку полюса также положим начало карандаша, а весь карандаш полностью прилегает к линейке. Теперь повернём карандаш так, чтобы его начало оставалось там же, на полюсе, а между ним и линейкой образовался некоторый угол поворота. Конец карандаша оказался в некоторой точке, назовём её M. Вот мы и получили полярные координаты точки M: длина карандаша и угол, на который был повёрнут карандаш. А теперь об этом же в более строгих и точных определениях.
Полярная система координат определяется заданием некоторой точки O, называемой полюсом, исходящего из этой точки луча OA (обозначается также и как Ox), называемого полярной осью, и масштаба для изменения длин. Кроме того, при задании полярной системы координат должно быть определено, какие повороты вокруг точки O считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).
Итак, выберем на плоскости (рисунок выше) некоторую точку O (полюс) и некоторый выходящий из неё луч Ox. Кроме того, укажем единицу масштаба. Полярными координатами точки M называются два числа ρ и φ, первое из которых (полярный радиус ρ) равно расстоянию точки M от полюса O, а второе (полярный угол φ, который называют также амплитудой) — угол, на который нужно повернуть против часовой стрелки луч Ox до совмещения с лучом OM.
Точку M с полярными координатами ρ и φ обозначают символом M(ρ, φ) .
Видео:A.6.6 Переход между декартовой и другими системами координатСкачать

Связь полярных координат с декартововыми координатами
Установим связь между полярными координатами точки и её декартовыми координатами. Будем предполагать, что начало декартовой прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка M имеет декартовы координаты x и y и полярные координаты ρ и φ.Тогда
Полярные координаты ρ и φ точки M определяются по её декартовым координатам следующим образом:

Для того, чтобы найти величину угла φ, нужно, используя знаки x и y, определить квадрант, в котором находится точка M, и, кроме того, воспользоваться тем, что тангенс угла φ равен 
Приведённые выше формулы называются формулами перехода от декартовых координат к полярным.
Одно из наиболее частых применений полярных координат в высшей математике — решения двойных интегралов в полярных координатах.
Видео:Полярная система координатСкачать

Задачи о точках в полярной системе координат
Пример 1. В полярной системе координат на плоскости даны точки
Найти полярные координаты точек, симметричных этим точкам относительно полярной оси.
Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полярной оси точки будет как и у данной точки. Как видно из рисунка в начале урока, при построении симметричной относительно полярной оси точки данную точку нужно повернуть вокруг полярной оси на тот же угол φ. Следовательно, в полярной системе координат второй координатой симметричной точки будет угол для исходной точки, взятый с противоположным знаком, то есть -φ. Итак, полярные координаты точки, симметричной данной относительно полярной оси будут отличаться лишь второй координатой, и эта координата будет с противоположным знаком. Полярные координаты искомых симметричных точек будут следующими:
Пример 2. В полярной системе координат на плоскости даны точки
Найти полярные координаты точек, симметричных этим точкам относительно полюса.
Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полюса точки будет как и у данной точки. Симметричная относительно полюса точка получается вращением исходной точки на 180 градусов против часовой стрелки, то есть на угол π. Следовательно, вторая координата точки, симметричной данной относительно полюса рассчитывается как φ + π (если в результате получится числитель больше знаменателя, то вычтем из полученного числа один полный оборот, то есть 2π). Получаем следующие координаты точек, симметричных данным относительно полюса:
Пример 3. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В полярной системе координат даны точки
Найти декартовы координаты этих точек.
Решение. Используем формулы перехода от полярных координат к декартовым:
Получаем следующие декартовы координаты данных точек:
Пример 4. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В декартовой прямоугольной системе координат даны точки
Найти полярные координаты этих точек.
Решение. Определяем первую из полярных координат по формуле 

🌟 Видео
Видеоурок "Преобразование координат"Скачать

Построение кривой в полярной системе координатСкачать

Полярные в декартовыеСкачать

Двойной интеграл в полярных координатахСкачать

Видеоурок "Полярная система координат"Скачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Семинар 5. Переход к полярным координатам.Скачать

Скорость и ускорение точки в полярных координатахСкачать

Полярные координатыСкачать

§53 Связь между полярными и декартовыми координатамиСкачать

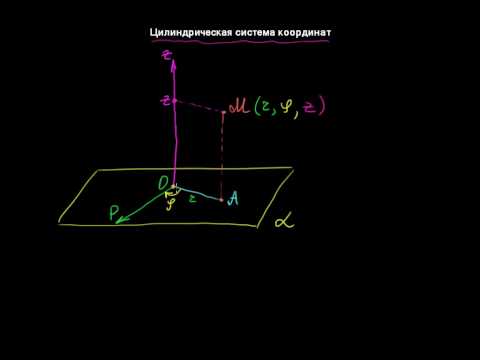
§55 Цилиндрическая система координатСкачать
§12 Полярное уравнение прямойСкачать

Часть 3 Задача определения формул перехода к новой декартовой системе координатСкачать

Полярные координаты. ТемаСкачать

§52 Полярная система координатСкачать