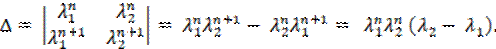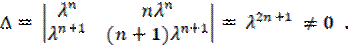Переход от дифференциального уравнения к разностному

Содержание:

Видео:Дифференциальные уравнения. 11 класс.Скачать

Разностные уравнения

Понятие разницы и разностного уравнения

Если для значений переменной x₁, x₂, x₃, . функция f (x) принимает значения f (x₁), f (x₂), f (x₃) . , то приращения функции составляют f (x₂) – f (x₁), f (x₃) – f (x₂), .

Приращение функции при переходе от значения x_i к значению x_i+1 будем обозначать: В частности можно взять в качестве значения независимых переменных x и x + 1 . Разность Δf (x) = f (x + 1) — f (x) называется первой разностью или разностью первого порядка. Она может рассматриваться в свою очередь как функция от x, а потому и для нее можно определить разницу:

Введем обозначения ΔΔf (x) = Δ 2 f (x), тогда Δ 2 f (x) = f (x + 2) — 2 f (x + 1) + f (x) и называется разностью второго порядка.

Аналогично можно найти разности третьего, четвертого и т. д. порядков.

Определим разности некоторых важнейших функций.

1) Если f (x) = С, где С — постоянная величина, то
Δf (x) = f (x + 1) – f (x) = С – С = 0.

Понятно, что и все разности следующих порядков будут также равняться нулю.

2) Если f (x) = ax + b, то
Δf = Δf (x + 1) — f (x) = a (x + 1) + b — ax — b = a.

Разница первого порядка линейной функции равна постоянной, а все остальные будут равны нулю.

3) Если f (x) = ax 2 + bx + c, то

Поскольку разница первого порядка является линейной функцией, то разница второго порядка — постоянная, а все последующие разности равны нулю.

4) Если f (x) = a x , то

В экономических исследованиях часто встречаются задачи, в которых время t является независимой переменной, а зависимая переменная определяется для времени t, t + 1, t + 2 и т. д.

Обозначим y_t — значение функции y в момент времени t; y_t+1 — значение функции в момент, сдвинутый на одну единицу, например, на следующий час, на следующую неделю и т. д., y_t+2 — значение функции y в момент, сдвинутый на две единицы и т. д.

Очевидно, что

Откуда:

За разность второго порядка, имеем или
поэтому

Аналогично можно доказать, что

Итак, любую функцию

можно представить в виде: (7.50)
и наоборот.

Определение. Уравнение
(7.51)
называется разностным уравнением n-го порядка.

Решить разностное уравнение n-го порядка — это значит найти такую ​​функцию y_t, которая превращает уравнение (7.50) или (7.51) в тождество.

Решение, в котором есть произвольная постоянная, называется общим; решение, в котором постоянная отсутствует, называется частным.

Определение. Уравнение
(7.52)
где a₀, a₁, . a_n — постоянные числа, называется неоднородным разностным
уравнением n-го порядка с постоянными коэффициентами.

Если в уравнении (7.52) f (t) = 0, то уравнение называется однородным разностным уравнением n-го порядка с постоянными коэффициентами:
(7.53)

Уравнение есть однородное разностное уравнение первого порядка с постоянными коэффициентами a и b, а уравнение — неоднородное разностное уравнение второго порядка с постоянными коэффициентами a, b, c.

ТЕОРЕМА 1. Если решениями однородного разностного уравнения (7.53) является y₁ (t) и y₂ (t), то его решением будет также функция y₁ (t) + y₂ (t).

ТЕОРЕМА 2. Если y (t) является решением однородного разностного уравнения (7.53), то его решением будет также функция Ay (t), где А — произвольная постоянная.

ТЕОРЕМА 3. Если y (t) — частное решение неоднородного уравнения (7.52) и y (t, A₁, A₂, . A_n) — общее решение однородного уравнения (7.53), то общим решением неоднородного разностного уравнения будет функция: y (t) + y (t, A₁, A₂, . A_n).

Эти теоремы схожи с теоремами для дифференциальных уравнений, которые были приведены нами в предыдущем разделе.

Разностные уравнения первого порядка с постоянными коэффициентами

Рассмотрим неоднородное разностное уравнение
(7.54)

Соответствующее ему однородное уравнение будет:
(7.55)

Возьмем функцию и убедимся, что она будет решением уравнения (7.55). Поскольку , тогда . Подставим y_t и y_t-1 в уравнение (7.55):
Итак, является решением уравнения (7.55).

По теореме (2) общее решение однородного разностного уравнения (7.55) является функция , где А — произвольная постоянная.

Пусть — частное решение неоднородного разностного уравнения (7.54). По теореме (3) общим решением неоднородного разностного уравнения (7.54) будет функция

Частное решение найти нетрудно, если f (t) = α, где α — некоторая постоянная. На самом деле, если где u — постоянная. Подставим в уравнение (7.54), имеем: u — au = α, откуда
Итак, общее решение уравнения (7.54) запишем в виде: .

Разностные уравнения второго порядка с постоянными коэффициентами

Пусть задано неоднородное разностное уравнение второго порядка с постоянными коэффициентами:
(7.56)
и соответствующее ему однородное уравнение
(7.57)

Убедимся, что функция будет решением уравнения (7.58). Подставим в уравнение (7.57) (λ ≠ 0), получим Поскольку λ ≠ 0, то поделим на λ t-2 , имеем λ 2 + aλ + b = 0 (7.58)

Это уравнение называется характеристическим уравнением для уравнения (7.57).

Здесь могут иметь место следующие три случая:

1. D = a 2 – 4b > 0, тогда уравнение (7.58) будет иметь два действительных различных корня.
Общее решение уравнения (7.57) запишется в виде:

а общее решение неоднородного уравнения (7.56) запишется так:

2. D = a 2 – 4b = 0, тогда и и

В этом случае однородное уравнение (7.57) примет вид:
(7.59)
Тогда

Легко убедиться, что решением уравнения (7.59) является также функция
Поэтому общим решением уравнения (7.59) является функция а общим решением неоднородного уравнения (7.56) функция

3. D = a 2 – 4b 2 – 5λ + 6 = 0 будет иметь действительные разные корни (D = 25 – 24 = 1 > 0), λ1 =2, λ2 = 3.
Общим решением однородного уравнения является функция

Далее положим, что y_t = y — частное решение неоднородного уравнения, тогда

Таким образом, общим решением неоднородного уравнения является функция Постоянные A₁ и A₂ определим из начальных условий: y₀ = 5, y₁ = 9. Тогда для t = 0 и t = 1 соответственно будем иметь:

Решим эту систему уравнений относительно A₁ и A₂:

Откуда

Итак, — общее решение заданного в условии разностного уравнения.

Примеры применения разностных уравнений в экономических задачах

Пример 1. Пусть некоторая сумма средств выдается под сложный процент p, то к концу t-го года ее размер будет составлять:
Это однородное разностное уравнение первого порядка. Его решением будет функция , где A — некоторая постоянная, которую можно найти из начальных условий.

Если положить y₀ = F , то A = F, откуда

Это известная формула величины фонда F, который выдается под сложный процент.

Пример 2. Пусть величина предложения сельскохозяйственной продукции в t-м году есть функция цены прошлого года а спрос на эту продукцию есть функция цены в этом году. Следовательно, спрос: а предложение

Цена равновесия для данной продукции определяется равенством:
а это разностное уравнение первого порядка.

Положим, что функция спроса определяется формулой а функция предложения — формулой

Цена равновесия запишется: то есть Решением этого уравнения является функция Постоянная A определяется из начальных условий, для t = 0 цена составляет p₀.

Тогда p₀ = A и решением уравнения является функция
Если начальная цена p₀ = 0, то p_t = 0 для всех значений t.

Следовательно, цена не подлежит изменению.

Вообще говоря, функция предложения — возрастающая, а потому b > 0; а функция спроса — убывающая, и поэтому a

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:6.3 Решение разностных уравненийСкачать

Переход от дифференциального уравнения к разностному

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии

Дифференциальные и разностные уравнения

Тема лекции: «Разностные (рекуррентные) уравнения второго порядка»

1. Линейные разностные уравнения k -го порядка.

2. Линейные разностные уравнения второго порядка с постоянными коэффициентами.

3. Модели экономической динамики с дискретным временем.

1. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ k -ГО ПОРЯДКА.

1.1. Определение разностного уравнения k -го порядка.

Теория разностных уравнений находит многообразные приложения во многих областях естествознания при моделировании поведения систем различной природы. Разностные уравнения обычно возникают тогда, когда рассматриваемая величина регистрируется через некоторые (как правило, равные) промежутки времени.

Например, так называемая паутинообразная модель рынка одного товара описывается разностным уравнением вида

где P_t — цена товара в период t , a и b — некоторые числа.

Уравнение (*) представляет собой линейное разностное уравнение первого порядка с постоянными коэффициентами.

В задачах описания, анализа и синтеза дискретных динамических систем управления математические модели таких систем описываются разнообразными разностными уравнениями.

В современной теории нелинейных колебаний разностные уравнения появляются либо самостоятельно, либо при переходе от дифференциальных уравнений к точечным отображениям Пуанкаре. Такой переход в трехмерном случае значительно упрощает исследование.

В математике основным источником разностных уравнений являются дифференциальные уравнения. Имеются в виду разностные схемы, используемые для приближенного решения дифференциальных уравнений.

Многие факты теории линейных дифференциальных уравнений верны и для линейных разностных уравнений, хотя есть и некоторые различия. Отличие разностных уравнений от дифференциальных уравнений проявляется в наибольшей степени, когда уравнения нелинейны. Например, поведение решений одномерных разностных уравнений может быть таким же сложным, как и поведение решений многомерных разностных уравнений. Для динамических систем, описываемых дифференциальными уравнениями, сложное поведение имеется лишь в пространствах большой размерности ( n > 3).

Приведем простейшие примеры разностных уравнений.

Разностное уравнение второго порядка

определяет признак арифметической прогрессии. Его решением является последовательность с общим членом

где a₁ — первый член арифметической прогрессии, и d – разность арифметической прогрессии.

определяет признак геометрической прогрессии, и его решением является последовательность с общим членом

где b₁ – первый член геометрической прогрессии, q – знаменатель геометрической прогрессии.

где k − фиксированное, а n − произвольное натуральное число, y_n , y_n+1 . y_n+k – члены некоторой числовой последовательности, называется разностным уравнением k-го порядка.

Решить разностное уравнение означает найти его общее решение, т.е. все последовательности y_n = y(n) , удовлетворяющие уравнению (1).

Разностные уравнения используются в моделях экономической динамики с дискретным временем, а также для приближенного решения дифференциальных уравнений.

Между теориями разностных и дифференциальных уравнений прослеживается определенная аналогия. Если в уравнении (1) произвести формальную замену:

то определение разностного уравнения преобразуется в общее определение обыкновенного дифференциального уравнения порядка k.

Проведя формальную замену (2), нетрудно получить нормальную форму записи разностного уравнения:

Аналогичным образом определяется и задача Коши – как задача нахождения решения уравнения (3), удовлетворяющего начальным условиям:

Ниже будет показано, что решения соответствующих классов дифференциальных и разностных уравнений (например, линейных) осуществляется схожими методами.

Теорема 1. Решение y_n = y(n) задачи Коши (3), (4) при n ≥ n₀ определено однозначно.

Доказательство. Подставляя значения для y(n₀) , y(n₀+1) , . , y (n₀+ k−1) из (4) в (3), мы находим y(n₀+k) . Это, в свою очередь, дает нам возможность определить y(n₀+k+1) .

Продолжая этот процесс, можно рекуррентным способом по формуле (3) найти любое значение y(n) при n ≥ n₀ . Теорема доказана.

Следует, однако, заметить, что нахождения общего решения разностного уравнения в отличие от задачи Коши является гораздо более сложной задачей.

1. 2. Линейные разностные уравнения k -го порядка.

Определение 2. Разностное уравнение вида

где a₀ ,a₁ . a_k , f − некоторые функции от n (a₀ ≠ 0, a_k ≠ 0), называется линейным разностным уравнением k-го порядка.

Условие a₀ ≠ 0 для всех n является существенным в определении линейного разностного уравнения первого порядка. Например, линейное разностное уравнение вида

не считается уравнением первого порядка, поскольку замена к+1 = m дает уравнение

которое условно можно назвать разностным уравнением нулевого порядка.

Введем следующее обозначение:

Это выражение называется линейным разностным оператором k-го порядка .

С учетом этих обозначений уравнение (6) может быть записано в виде:

называется линейным однородным разностным уравнением, соответствующим уравнению (7). Само же уравнение (7) (при f(n) ≠ 0) называется неоднородным .

Имеют место следующие утверждения.

Теорема 2 (об общем решении линейного неоднородного уравнения).

Общее решение линейного неоднородного разностного уравнения (7) есть сумма частного решения ȳ (n) этого уравнения и общего решения y ₀( n ) соответствующего ему однородного уравнения (8).

Теорема 3 (об общем решении линейного однородного уравнения).

Пусть у (1) (n), . у (k) (n) – система, состоящая из k линейно независимых решений линейного однородного разностного уравнения (8), тогда общее решение этого уравнения задается формулой:

Множество решений линейного однородного разностного уравнения k-го порядка образует k- мерное линейное пространство, а любой набор у (1) (n), . у (k) (n) из k линейно независимых решений (называемый фундаментальным набором) является его базисом.

Признаком линейной независимости решений у (1) (n), . у (k) (n) однородного уравнения является неравенство нулю определителя Казорати:

∆ = det y n (1) ⋯ y n ( k ) ⋮ ⋱ ⋮ y n + k (1) ⋯ y n + k ( k ) 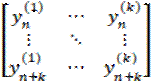, (10)

который является аналогом определителя Вронского в теории обыкновенных дифференциальных уравнений.

1.3. Линейные однородные разностные уравнения с постоянными коэффициентами k -го порядка.

В случае, когда коэффициенты a₀ , a₁ . a_k являются постоянными, методы решения линейного однородного разностного уравнения

во многом аналогичны методам решения дифференциальных уравнений с постоянными коэффициентами.

Действительно, будем искать решения уравнения в виде:

где λ ≠ 0 – некоторая постоянная. Подставляя выражение для y_n из (12) в (11), находим:

a_k λ n + k + a_{k −1} λ n + k −1 + … + a ₁ λ n +1 + a ₀ λ n = 0 .

Разделим обе части этого уравнения на λ n , получим:

Уравнение (13) называется характеристическим уравнением однородного линейного разностного уравнения.

Так же, как и в случае линейных дифференциальных уравнений с постоянными коэффициентами, знание корней характеристического уравнения, позволяет построить общее решение однородного разностного уравнения.

2. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.

Рассмотрим линейное разностное уравнение второго порядка с постоянными коэффициентами

Построим решения этого уравнения в зависимости от значения D = b 2 − 4 ac . Однако заметим, что полученные в этом случае результаты могут быть без труда перенесены на случай уравнений более высокого порядка.

В зависимости от значения дискриминанта

a λ 2 + b λ + c = 0 (15)

возможны следующие случаи.

Характеристическое уравнение (15) имеет два действительных и различных корня – λ₁ и λ₂ . Тогда λ₁ ≠ 0 и λ₂ ≠ 0 . Действительно, если хотя бы один корень равен нулю, то коэффициент приведенного квадратного уравнения (15`) c / a = λ₁ λ₂ также будет равен нулю, что противоречит определению линейного разностного уравнения второго порядка.

Корням λ₁ и λ₂ характеристического уравнения соответствуют два решения:

Покажем, что эти решения линейно независимы. Для этого вычислим определитель Казорати

∆ = det y n (1) ⋯ y n ( k ) ⋮ ⋱ ⋮ y n + k (1) ⋯ y n + k ( k )

В данном случае получим

∆ = λ 1 n λ 2 n λ 1 n +1 λ 2 n +1 = λ 1 n λ 2 n +1 — λ 2 n λ 1 n +1 = λ 1 n λ 2 n λ 2 — λ 1 .

Так как корни λ₁ и λ₂ различны, то λ₂ − λ₁ ≠ 0 , следовательно, ∆ ≠ 0 , а значит, решения линейно независимы.

В этом случае общее решение уравнения имеет вид:

где C₁ , C₂ – произвольные постоянные.

Решение примера 3.

Составим характеристическое уравнение, имеем:

Оно имеет два действительных различных корня: λ₁ = 1 , λ₂ = − 5 . Поэтому общее решение исходного уравнения в силу формулы (16) имеет вид:

Решение примера 4.

Составим характеристическое уравнение, имеем:

Оно имеет два действительных различных корня: λ₁ = 3 , λ₂ = 2 . Поэтому общее решение исходного уравнения в силу формулы (16) имеет вид:

Характеристическое уравнение имеет два комплексно сопряженных корня: λ₁ и λ₂ ,

которые, используя тригонометрическую форму записи, могут быть представлены следующим образом:

где r – модуль λ₁ , а φ – его аргумент:

Соответствующие решения разностного уравнения также комплексно сопряжены и на основании формулы Муавра имеют вид:

y (1) _n = r n (cos n φ + i sin n φ ) , y (2) _n = r n (cos n φ − i sin n φ ) .

Чтобы получить действительные решения, заменим y n ( 1 ) и y n ( 2 ) их линейными комбинациями:

Таким образом, мы получили два линейно независимых действительных решения:

z (1) _n = r n cos(n φ ) , z (2) _n = r n sin(n φ ) .

Таким образом, в данном случае общее решение имеет вид:

y(n) = r n ( C₁ cos (n φ )+ C₂ sin (n φ ) ) . (17)

Решение примера 5.

имеет два комплексно сопряженных корня –

которые могут быть записаны как:

λ ₁ = 2 (cos ( π /3) + i sin( π /3)), λ ₂ = 2 (cos ( π /3) – i sin( π /3))

Следовательно, общим решением исходного уравнения в силу формулы (17) будет:

Оба корня характеристического уравнения действительны и равны ( λ₁ = λ₂ = λ ) .

Покажем, что в этом случае кроме решения

существует еще одно решение, линейно независимое с y _n (1) .

Действительно, нетрудно убедится, что таковым является:

Сначала докажем, что y_n (2) является решением уравнения (14).

В самом деле, подставляя выражение для y_n (2) в уравнение (14) , получим:

a(n+2) λ n+2 + b(n+1) λ n+1 + cn λ n = λ n (a (n+2) λ 2 + b(n+1) λ + cn) =

= λ n (n (a λ 2 + b λ + c) + 2a λ 2 + b λ ) = 0

Последнее равенство получим в силу того, что aλ 2 + bλ + c = 0 и λ = − b /2 a .

Вычислим теперь определитель Казорати, мы имеем:

∆ = λ n n λ n λ n +1 ( n +1) λ n +1 = λ 2 n +1 ≠ 0 .

так как λ ≠ 0 . Следовательно, частные решения y_n (1) и y_n (2) линейно независимы, и общее решение уравнения (147) имеет вид:

Решение примера 6.

имеет единственный действительный корень

λ = − 3 . Следовательно, общее решение исходного уравнения таково:

Для нахождения решения неоднородного линейного разностного уравнения, так же как и в случае линейных дифференциальных уравнений, используется метод неопределенных коэффициентов, основанный на подборе частного решения неоднородного уравнения по виду правой части f(n) .

Проиллюстрируем нахождение решения неоднородного линейного разностного уравнения на примерах.

Решение примера 7.

Будем искать частное решение в виде:

Подставляя это выражение в наше уравнение (19), получим:

p (25 + 10 – 3)5 n = 64 ∙ 5 n .

Следовательно, p = 2, а значит, y*(n) = 2 ∙ 5 n .

Решая характеристическое уравнение

Общее решение однородного уравнения имеет вид:

Таким образом, общее решение неоднородного уравнения (19) имеет вид:

y( n +2) – 7y( n +1) + 10y( n ) = 4 ∙ 6 n . (20)

Решение примера 8.

Для нахождения общего решения соответствующего однородного уравнения составим характеристическое уравнение:

Для нахождения частного решения y*( n ) исходного уравнения воспользуемся методом неопределенных коэффициентов. Будем искать

Подставляя это выражение в данное уравнение (20), получим:

p6 n+2 –7 p6 n+1 + 10 p6 n = 4 ∙ 6 n .

p 6 n (36 – 42 +10) = 4 ∙ 6 n .

Следовательно, p = 1, а значит, частное решение уравнения (20) имеет вид:

Складывая общее решение соответствующего однородного уравнения и частное решение неоднородного уравнения (20), получаем общее решение уравнения:

y ( n ) = 6 n + С₁ 5 n + С₂ 2 n .

3. МОДЕЛИ ЭКОНОМИЧЕСКОЙ ДИНАМИКИ С ДИСКРЕТНЫМ ВРЕМЕНЕМ

3.1. Модель делового цикла Самуэльсона–Хикса

Рассмотрим пример, иллюстрирующий применение разностных уравнений второго порядка. Для этого мы рассмотрим модель делового цикла Самуэльсона – Хикса (динамический вариант модели Кейнса). Эта модель основывается на принципе акселерации, то есть на предположении, что объемы инвестирования прямо пропорциональны приросту национального дохода. Данное предположение характеризуется следующим уравнением:

где коэффициент V > 0 − фактор акселерации, I (t) – величина инвестиций в период t, Y (t−1) , Y (t−2) – величины национального дохода соответственно в (t−1) -м и (t−2) -м периодах.

Предполагается также, что спрос на данном этапе зависит от величины национального дохода на предыдущем этапе, то есть:

C(t) = aY(t−1) + b . (22)

Условие равенства спроса и предложения имеет вид:

Подставляя в (23) выражение для I (t) из (21) и выражение для C(t) из (22), находим:

Y(t) = (a+V)Y(t−1) − VY(t−2) + b . (24)

Уравнение (24) известно, как уравнение Хикса.

Если предположить, что на протяжении рассматриваемых периодов величины a и V постоянны, то уравнение Хикса представляет собой неоднородное линейное разностное уравнение второго порядка с постоянными коэффициентами.

Мы можем легко найти частное решение уравнения (24), если положим, что:

Y (t) = Y(t−1) = Y(t−2) = Y* , (25)

т.е. использовав в качестве частного решения равновесное решение Y* = const .

Из (24) в силу (25) имеем:

Выражение (1−a) −1 в формуле (26) носит название мультипликатора Кейнса и является одномерным аналогом матрицы полных затрат.

Рассмотреть модель Самуэльсона–Хикса при условии, что

a = 0,5 ; V = 0,5; b = 4 .

Найти общее решение уравнения Хикса.

Решение примера 9.

В этом случае уравнение (24) принимает вид:

Y(t) − Y(t−1) + 0,5 Y(t−2) = 4 .

Его частным решением (в силу формулы (26)) будет:

Y * (t) = b /(1- a ) = 4/(1 — 0,5) = 8.

Найдем корни характеристического уравнения

λ _1,2 = (1 ± i)/2 = (1/ √ 2) (cos ( π /4) ± i sin ( π /4)) .

Таким образом, общим решением соответствующего однородного уравнения является:

Следовательно, общим решением уравнения будет:

В зависимости от значений а и V возможны четыре типа динамики. Она может быть растущей или затухающей и при этом иметь или не иметь колебательный характер. Так, в рассмотренном выше примере динамика носила колебательный характер с возрастающей амплитудой.

Рассмотреть модель Самуэльсона – Хикса при условии, что

a = 0,48, V = 0,72, b = 1,3.

Найти общее решение уравнения Хикса.

Решение примера 10.

В данном случае уравнение (24) имеет вид

Y(t) – 1,2Y (t−1) + 0,72 Y(t−2) = 1,3 .

Его частным решением (в силу формулы (26)) будет:

y * (t) = b /(1- a ) = 1,3/(1 — 0,48) = 2,5.

Напишем характеристическое уравнение:

λ 2 – 1,2 λ + 0,72 = 0 .

λ_1,2 = 0,6 ± 0,6 i = 0,6 √ 2 ( cos ( π /4) ± i sin ( π /4)).

Общее решение соответствующего однородного уравнения есть

Ŷ ₀( t ) = (0,6 √ 2) t ( С₁ cos ( t π/4) + С₂ sin (t π/4) ).

Получаем общее решение данного уравнения:

В рассмотренном примере динамика носит колебательный характер с затухающей амплитудой. Очевидно, при комплексных сопряженных корнях характеристического уравнения, по модулю превышающих единицу, динамика была бы растущей. Вообще,

в зависимости от значений a и V динамика может быть растущей или затухающей и при этом иметь или не иметь колебательный характер.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

[1] Васенкова Е.К., Волкова Е.С, Шандра Е.Г. Математика для экономистов. Дифференциальные и разностные уравнения: Курс лекций. М.: Финансовая академия, 2003. 116 с.

[2] Клюшин В. Л. Высшая математика для экономистов: Учебное пособие. — М.: ИНФРА-М, 2009. — 448 с. — (Учебники РУДН).

[3] Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. — 2-е изд., испр. — М.: Дело, 2001. — 688 с.

[4] Ласунский А.В. Разностные уравнения: Конспект лекций. ФГБОУ ВПО «Новгородский государственный университет им. Ярослава Мудрого», Великий Новгород, 2011.– 62с.

[5] Романко В.К . Разностные уравнения. Учебное пособие. БИНОМ. Лаборатория знаний, 2006. — 112 с.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

11 Замена дифференциального оператора разностным аналогом

Замена дифференциального оператора разностным аналогом.

Эту процедуру легко проиллюстрировать на следующем простом примере. Пусть непрерывная функция , определенная на отрезке (рис. 1, а), описывается дифференциальным уравнением

(1)

где А — константа; задано также граничное условие и при дискретизации области была построена сетка с постоянным шагом h.

Заменим дифференциальный оператор разностным:

(2)

Где — правая разностная производная.

Подставив (2) в (1), получим разностное уравнение

(3)

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Рекомендуемые файлы

Умножив (3) на h и полагая последовательность х=0, h, 2h, …, перейдем к системе алгебраических уравнений:

(4)

Решая (4) относительно сеточной функции, найдем таблицу значений, аппроксимирующую решение краевой задачи (1). При уменьшении шага h сетка становится все «гуще», а таблица значений сеточной функции — все подробнее. При неограниченном стремлении шага к нулю можно было бы получить значение искомой функции в каждой точке области. Но, в реальных случаях степень приближения к точному решению ограничивается рядом факторов, важнейшим из которых является размерность результирующей системы уравнений (4).

Для аппроксимации дифференциального оператора разностным кроме (2) часто пользуются выражением:

(5)

Где — левая разностная производная.

Кроме того, для аппроксимации , можно воспользоваться любой линейной комбинацией (2)-(5), т.е.

Где — любая вещественная константа.

При дифференциальный оператор аппроксимируется центральной разностной производной.

(6)

Подставив (6) в (1), получим другой разностный аналог краевой задачи (1):

.

Удобным геометрическим изображением схем построения разностных производных являются шаблоны.

На рис. 2 приведены шаблоны, соответствующие правой (рис. 2, а), левой (рис.2, б) и центральной (рис. 2, в) разностным производным.

Рис. 2. Примеры шаблонов в одномерной области, соответствующих разностным производным: а – правой, б – левой, в – центральной.

При переходе от дифференциальной краевой задачи к разностной необходимо также аппроксимировать граничные условия. В рассмотренном примере (1) граничные условия при использовании (2) можно аппроксимировать точно:

(7)

Совокупность разностного уравнения и разностных краевых условий называется разностной схемой краевой задачи.

В нашем примере уравнения (3) и (7) являются разностной схемой краевой задачи (1).

Кажущаяся простота построения разностной схемы в рассмотренном примере обманчива. В реальных задачах при построении разностных схем возникают проблемы. При исследовании разностных схем даже простых линейных задач часто выясняется, что разностная схема дает решение, не сходящееся при измельчении сетки к точному решению дифференциальной задачи. Поэтому построение сходящейся разностной схемы – центральный и наиболее сложный вопрос МКР.

Понятие сходимости разностной схемы тесно связано с понятиями точности и устойчивости.

Пусть точное значение непрерывной функции в узле с координатой x=x_h равно , а полученное значение точной функции в том же узле . Если погрешность стремится к нулю при стремлении к нулю шага h и имеет k-й порядок относительного шага, то принято говорить, что разностная схема имеет k-й порядок точности в n-м узле.

Аналогично для определения порядка аппроксимации вычисляют погрешность между точным и приближенным значениями производной в n-м узле:

Лекция «32 Русская культура XVIII века» также может быть Вам полезна.

При этом порядок погрешности относительно шага впадает с порядком аппроксимации дифференциального разностным оператором в n-м узле.

Для определения порядка точности многих практических разностных схем достаточно определить порядок аппроксимации дифференциального оператора разности, так как порядки точности и аппроксимации для них совпадают. Однако разностная схема, для которой такое подтверждение может быть доказано, должна обладать еще одним важным свойством — устойчивостью.

Устойчивая разностная схема — схема, в которой не происходит наращивания малых ошибок округления, допущенных на начальных стадиях решения.

Для многих краевых задач сходимость разностной схемы является следствием аппроксимации ею краевой задачи и устойчивости. При этом порядок сходимости относительно шага совпадает с порядком аппроксимации.

Для гладких неразрывных функций хорошо развит математический аппарат изучения аппроксимации и доказательства устойчивости разностных схем.

Необходимость исследования сходимости впервые построенной разностной схемы обусловливает тот факт, что основу программных реализаций в САПР составляют вполне конкретные, хорошо изученные для определенных задач разностные схемы.

📺 Видео

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Разностное функциональное уравнение решено двумя способами.Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Дифференциальные уравнения с разделенными переменными. 11 класс.Скачать

Дифференциальные уравнения с разделяющими переменными. 11 класс.Скачать

Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

6-2. Метод сетокСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать