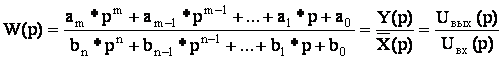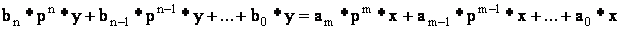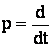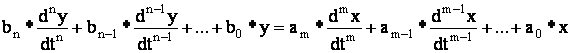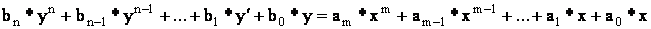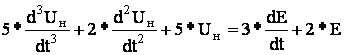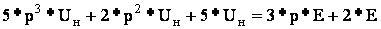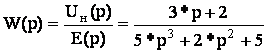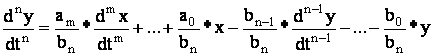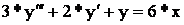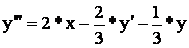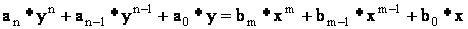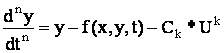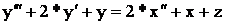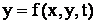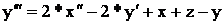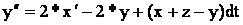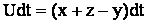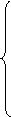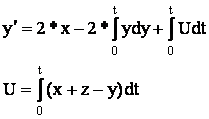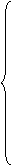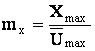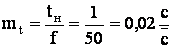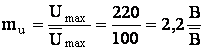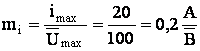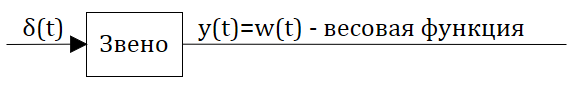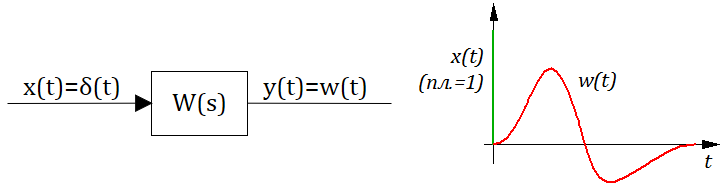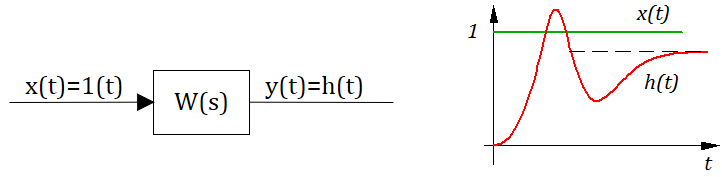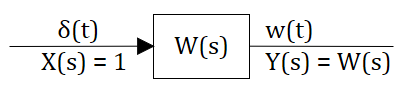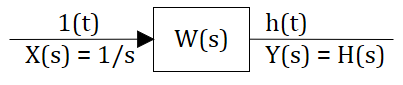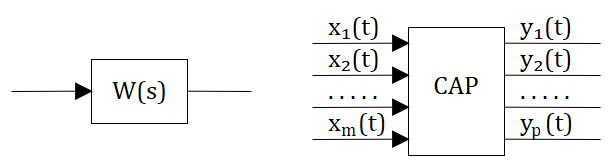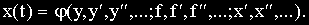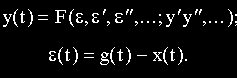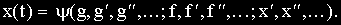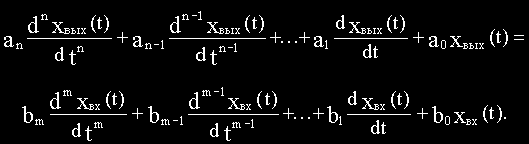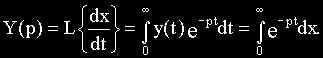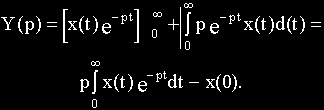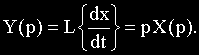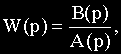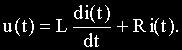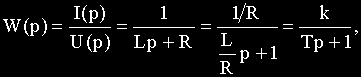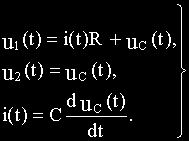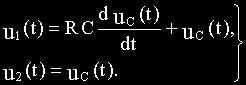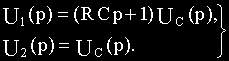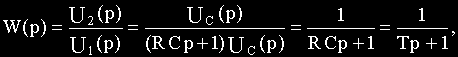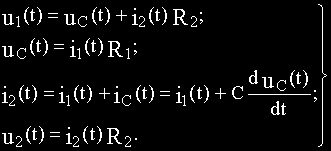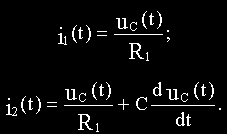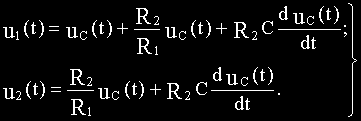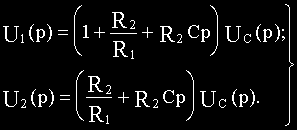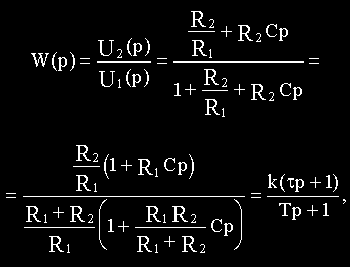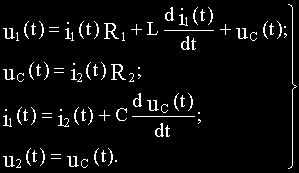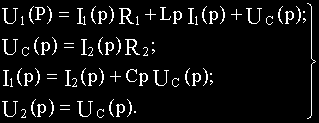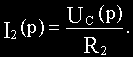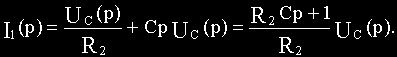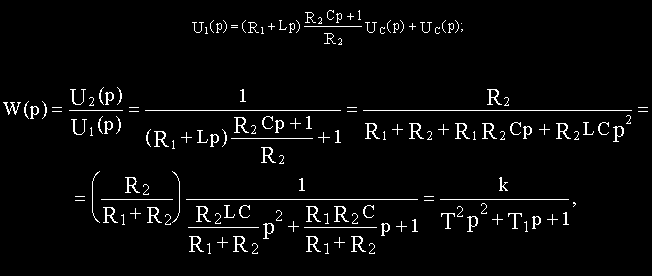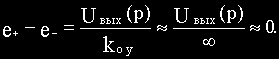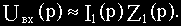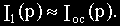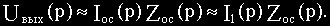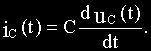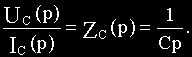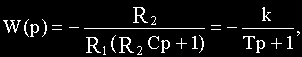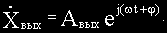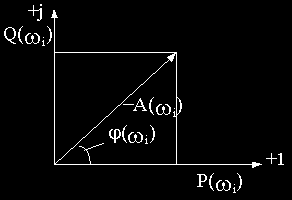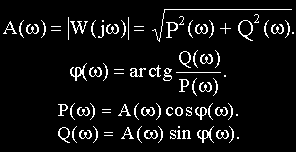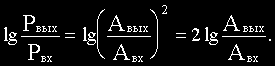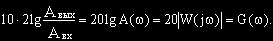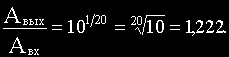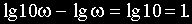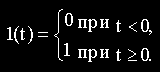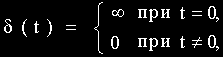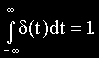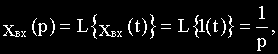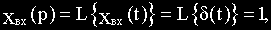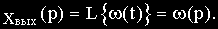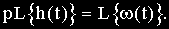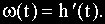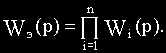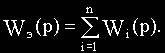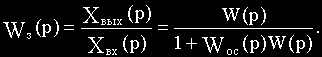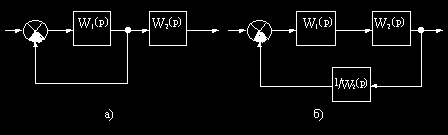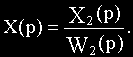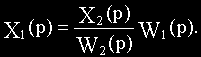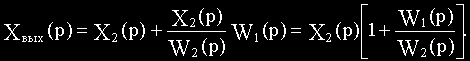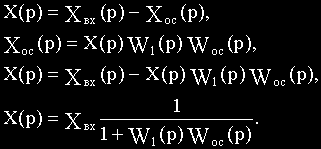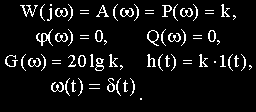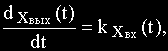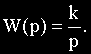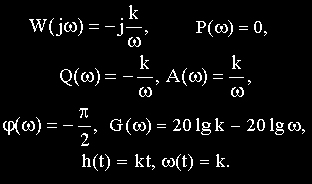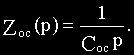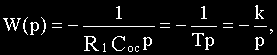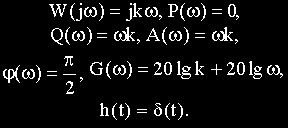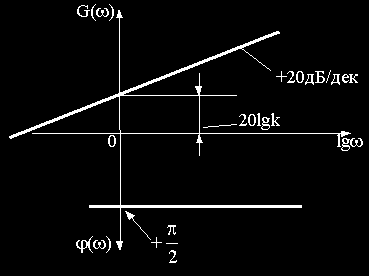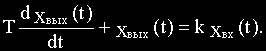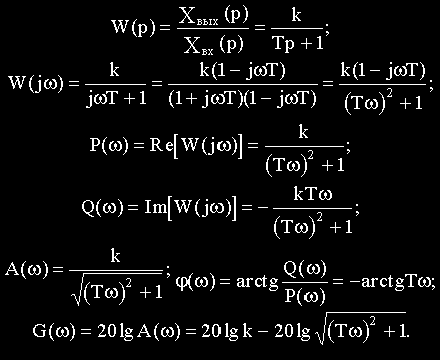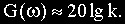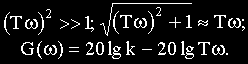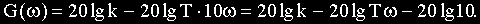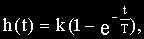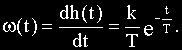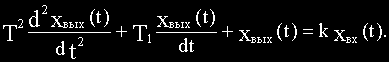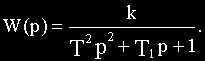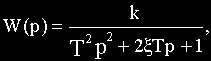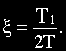Переход от дифференциального уравнения к передаточной функции и обратно (6 видео)

Переход от передаточной функции к дифференциальному уравнению

Содержание

Страницы работы
Содержание работы
2. Математическое описание систем автоматического управления ч. 2.9 — 2.13
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)
Пример
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона
2.12. Mетод переменных состояния.
Пример решения задачи в форме коши.
2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно
2.13.1. Правая часть содержит только b0*u(t)
2.13.2. Правая часть общего вида
Пример:
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САУ
2.2. Частотные характеристики
2.3. Временные функции и характеристики
2.4. Структурные схемы и их преобразование
2.5. Типовые звенья и их характеристики
2.7. Частотные характеристики разомкнутых систем
🔥 Видео

Страницы работы

Содержание работы

ПЕРЕХОД ОТ ПЕРЕДАТОЧНОЙ ФУНКЦИИ

К ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ

Решение обратной задачи: от системы уравнений перейти к одному уравнению, в котором присутствуют выходная величина и входная величина.

При этом 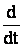заменить на р.

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ НА АВМ

1. Составление математической модели объекта (его математическое описание в виде системы дифференциальных уравнений).

2. Приведение уравнений к виду удобному для моделирования.

3. Масштабирование переменных, расчет коэффициентов передачи решающих усилителей и получение уравнений в машинном виде.

4. Составление структурной схемы модели.

5. Набор и настройка модели на АВМ.

6. Пробное решение контрольной задачи.

7. Выполнение программы исследования.

8. Анализ результатов и выводы.

ПРИВЕДЕНИЕ УРАВНЕНИЙ К ВИДУ УДОБНОМУ ДЛЯ МОДЕЛИРОВАНИЯ.

МЕТОД ПОНИЖЕНИЯ ПОРЯДКА ПРОИЗВОДНОЙ

Приведение уравнений к виду удобному для моделирования – это разрешение уравнений системы относительно старшей производной системы уравнений.

1) В правой части уравнения отсутствуют производные по х.

Вид удобный для моделирования:

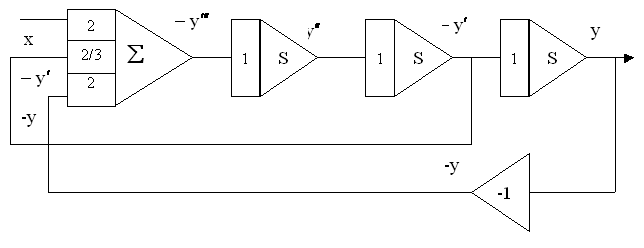
Метод понижения порядка производной, который заключается в том, что с помощью сумматора реализуется старшая производная выходной величины, а затем путем последовательного интегрирования получают производные более низких порядков и саму выходную величину.

2) В правой части уравнения имеются производные по входным величинам.

где x(t), z(t) – входные величины.

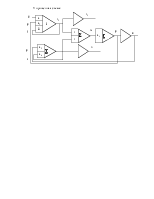
Переход от дифференциального уравнения к передаточной функции и обратно

Приводим к виду удобному для моделирования:

Схема аналоговой модели:

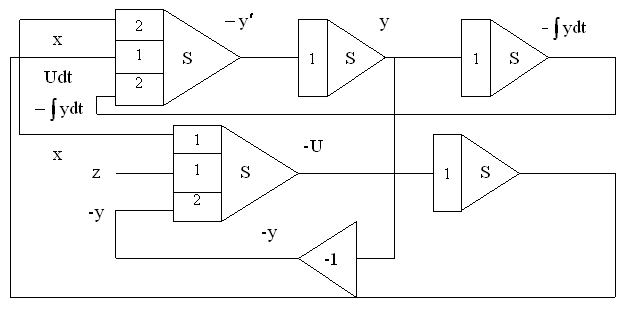МАСШТАБИРОВАНИЕ ЗАВИСИМЫХ И НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ.

РАСЧЕТ КОЭФФИЦИЕНТОВ ПЕРЕДАЧИ РЕШАЮЩИХ УСИЛИТЕЛЕЙ.

СОСТАВЛЕНИЕ МАШИННЫХ УРАВНЕНИЙ

;

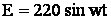
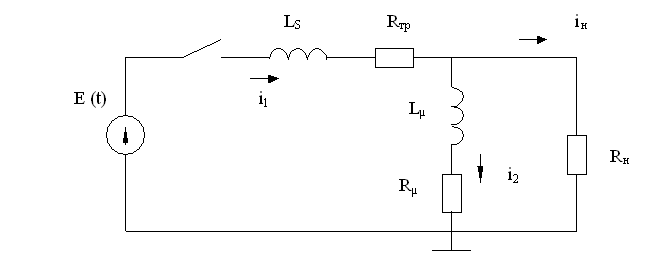
L_S = 20 мГн = 0,02 Гн;

Необходимо разработать аналоговую модель объекта:

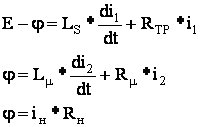
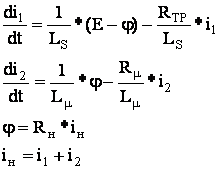
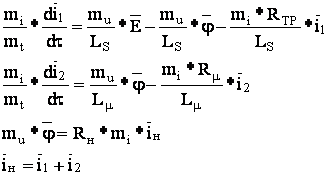
1. Составляем математическое описание цепи, используя метод узловых потенциалов:

Приводим к виду удобному для моделирования, т.е. решаем относительно старшей производной:

Операция масштабирования переменных.

1. Приведение всех зависимых переменных к виду напряжений.

2. Величины напряжений не должны превышать максимально допустимой величины для данной АВМ (100 В).

3. Масштабирование независимой переменно (времени) решает задачу удобства наблюдения результатов моделирования при минимальных затратах времени на моделирование.

Для определения масштабов определяют максимальные значения переменных. При определении максимальных значений исходят из наиболее жестких режимов для данной цепи. Уточнение – решение контрольной задачи.

1. U_max = Е = 220 В

с -1

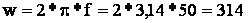
2. i_max – режим короткого замыкания в нагрузке:

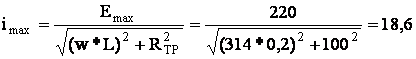
Принимаем i_max = 20 А.

4. Переходим к машинным переменным.

В системе уравнений, описывающих объект, заменим реальные переменные на машинные, умноженные на масштаб.

Избавимся от масштабов в левой части:

Определим коэффициенты передачи решающих усилителей:

Видео:Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

2. Математическое описание систем автоматического управления ч. 2.9 — 2.13

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В предыдущих сериях:

В это части будут рассмотрены:

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.

Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)

Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1

Предположим, что уравнение динамики имеет вид:

где: — постоянные времени;
— коэффициент усиления.

Пусть известны отображения:

Найдем изображения для производных:

Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:

B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.

Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.

После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.

Пример

Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:

входное воздействие: — единичное ступенчатое воздействие.

Выполним преобразование Лапласа:

Подставим в уравнение динамики и получим уравнение динамики в изображениях:

Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:

2.10. Весовая и переходная функции звена (системы).

Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.

Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.

На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:

Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.

Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):

тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:

Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:

2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона

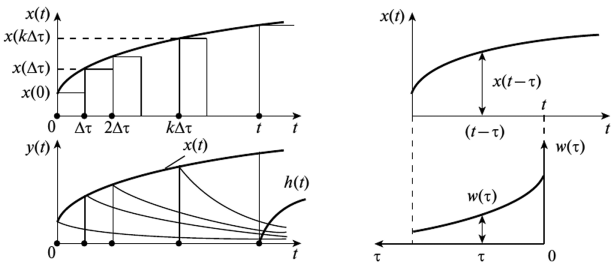
Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).

Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:

где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.

Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:

Переходя к пределам

если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:

где — вспомогательное время

Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:

Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:

2.12. Mетод переменных состояния.

До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)

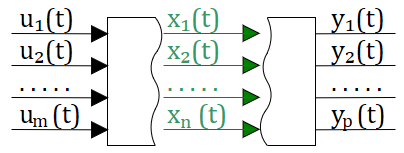
В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2

В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:

Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:

где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;

Данная система уравнений может быть записана в матричной форме:

где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;

В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.

Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования

Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.

Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики

Пример решения задачи в форме коши.

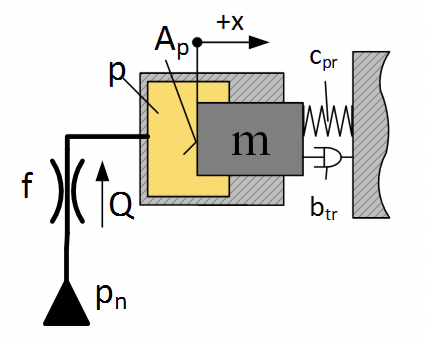
Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:

Дано:
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см 3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м 3 .
Определить:
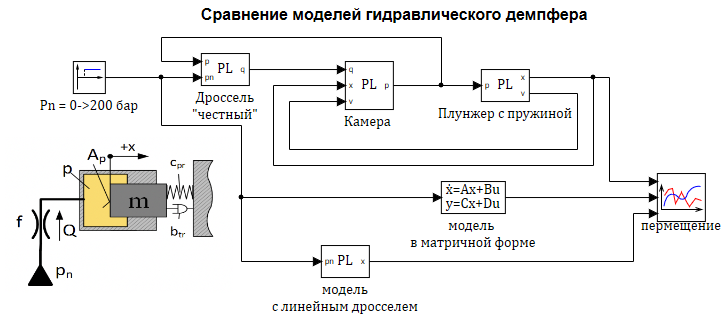
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13

Уравенение движение плунжера:

Где: – площадь плунжера, – жесткость пружины, – коэффициент вязкого трения, p – давление в камере.

Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда

Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:

Где: Q – расход в камеру, V — объем камеры.

Расход через дроссель:

Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:

Подставляем линеаризованную формул расхода в формулу давления:

Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:

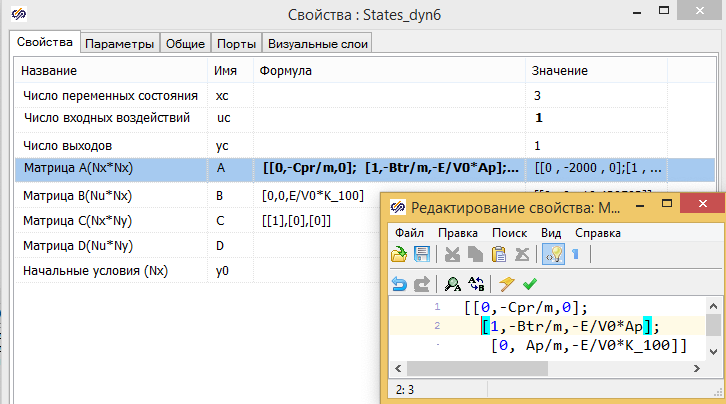
Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:

Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.

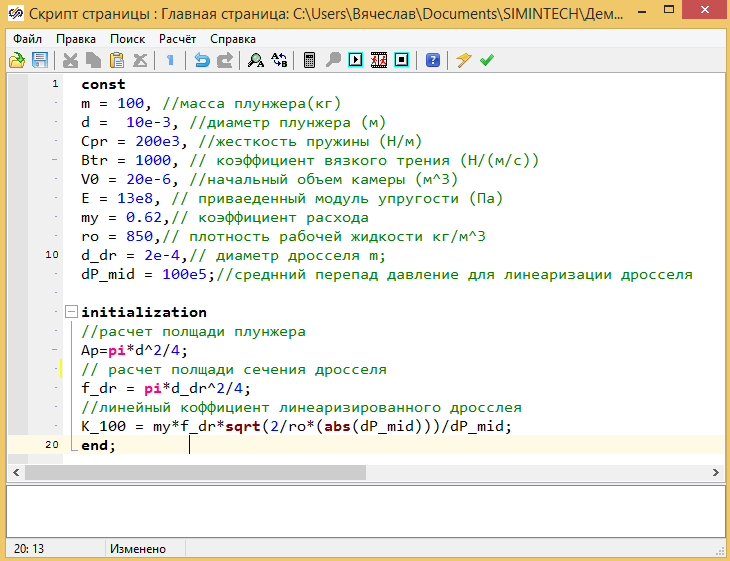
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:

Рисунок 2.12.5 Глобальный скрипт проекта.

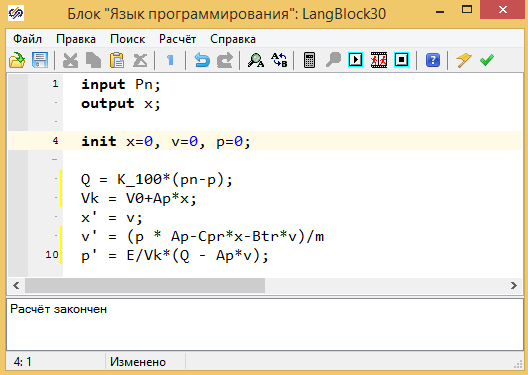
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)

Рисунок 2.12.6 Скрипт расчета модели в форме Коши.

Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7

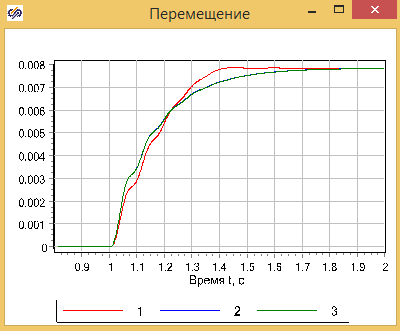
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)

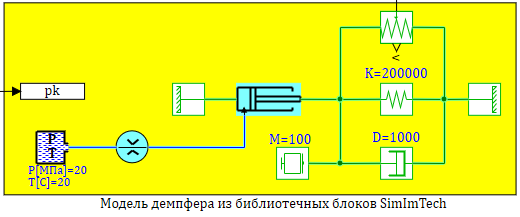
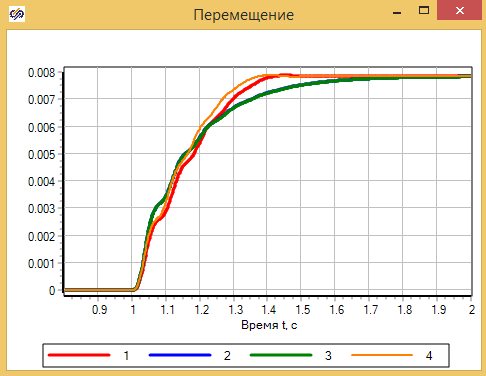
Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10

На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.

2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно

Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:

Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:

2.13.1. Правая часть содержит только b₀*u(t)

В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.

Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:

Для перехода к форме Коши ведем новые переменные:

И перепишем уравнение относительно y»'(t):

Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:

Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:

2.13.2. Правая часть общего вида

Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:

Сделаем преобразования: перейдем к уравнениям динамики в изображениях:

Тогда можно представить уравнение в изображениях в виде:

Разделим уравнение в изображениях на произведение полиномов , получим:

Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что отображение величины . Тогда входная величина может быть в изображениях представлена как:

Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.

А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:

Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :

А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:

Перейдем от изображения к оригиналам:

Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:

Пример:

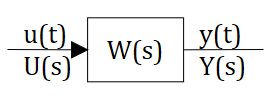
Рисунок 2.13.1 Передаточная функция.

Имеется передаточная функция (рис. 2.13.1) в изображениях :

Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши

В изображения реакция системы связана с входным воздействие соотношением:

Разделим в последнем правую и левую часть на произведения , и введем новую перменную :

Полиномы N(s) и L(s) равны:

Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):

Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:

Или в матричной форме:

Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:

Перейдем от изображений к оригиналу:

Таким образом второе уравнение матричной системы выглядит так:

Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2

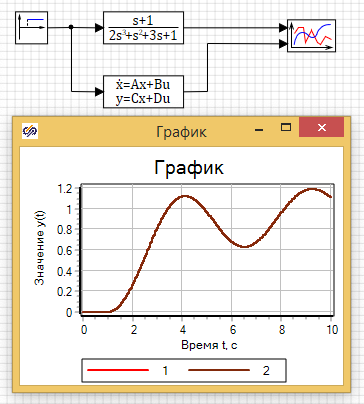
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.

Видео:[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САУ

Рассмотрим случай, когда в замкнутой системе можно выделить объект О и управляющее устройство УУ, как показано на рисунке ниже.

Общее уравнение САУ получается из системы уравнений объекта и управляющего устройства.

Состояние объекта характеризуется выходной величиной x(t), регулирующим воздействием y(t) и возмущением f(t). Тогда выходная величина может быть представлена функцией:

Состояние управляющего устройства характеризуется регулирующим воздействием y(t) и входным воздействием ε(t). Процессы в УУ будут описываться двумя уравнениями:

Три последних уравнения полностью описывают процессы в САУ. Если в этих уравнениях исключить переменные y(t) и ε(t), то получим дифференциальное уравнение САУ:

Это уравнение оценивает состояние системы во времени, определяет переходные процессы и обычно называется уравнением динамики. Однако в форме дифференциальных уравнений математическое описание в теории автоматического управления обычно не применяется вследствие сложности решения таких уравнений.

Исследование САУ существенно упрощается при использовании прикладных математических методов операционного исчисления. Возьмем некоторый элемент САУ, имеющий один вход и один выход. Дифференциальное уравнение элемента в общем случае имеет вид:

Если в этом уравнение вместо функции времени x_вых(t) и x_вх(t) ввести функции X_вых(p) и X_вх(p) комплексного переменного р, поставив условием, что эти функции связаны зависимостями:

(2.2)

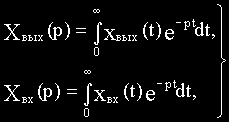
то оказывается, что дифференциальное уравнение, содержащее функции x_вых(t) и x_вх(t) при нулевых начальных условиях, равносильно линейному алгебраическому уравнению, содержащему функции X_вых(p) и X_вх(p):

Такой переход от дифференциального уравнения к однозначно соответствующему ему алгебраическому уравнению называется преобразованием Лапласа.

Функция X(p) называется изображением функции x(t), функция x(t) называется оригиналом функции X(p).

Операция перехода от искомой функции x(t) к ее изображению X(p) (нахождение изображения от оригинала) называется прямым преобразованием Лапласа и записывается условно с помощью символа L как

Операция перехода от изображения X(p) к искомой функции x(t) (нахождение оригинала по изображению) называется обратным преобразованием Лапласа и записывается условно с помощью символа L -1 как

Формально переход от дифференциального уравнения к алгебраическому относительно изображения при нулевых начальных условиях получается путем замены символов дифференцирования оригиналов функций d n /dt n , d n-1 /dt n-1 . d/dt соответственно на p n ,p n-1 . p и функций x(t)— их изображениями X(p). С комплексной переменной p, как и с другими членами алгебраического уравнения, можно производить различные действия: умножение, деление, вынесение за скобки и т.д.

Так как возможность однозначного перехода от дифференциального уравнения к алгебраическому значительно упрощает расчеты, то важно убедиться в правомерности такого перехода.

Обозначим в исходном дифференциальном уравнении 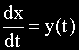и согласно интегралу (2.2) найдем изображение:

Согласно правилу интегрирования по частям

При нулевых начальных условиях x(0)=0 и с учетом (2.2) получим:

Таким образом, операция дифференцирования оригинала соответствует операции умножения изображения этого оригинала на комплексное число p.

Каждый элемент САУ в общем случае описывается дифференциальным уравнением вида (2.1). Следовательно, при выводе дифференциального уравнения системы в целом необходимо совместно решить несколько дифференциальных уравнений высших порядков.

Преобразование дифференциальных уравнений по Лапласу позволяет свести эту задачу к решению системы алгебраических уравнений. Определив из алгебраических уравнений изображение X(p) искомой функции x(t), определяющей переходной процесс в системе, находят эту функцию, пользуясь таблицами оригиналов и изображений или по известным формулам обратного преобразования Лапласа.

Кроме того, преобразование дифференциального уравнения по Лапласу дает возможность ввести понятие передаточной функции.

Вынеся в уравнении (2.3) X_вых(p) и X_вх(p) за скобки, получим:

Определим из этого уравнения отношение изображения выходной величины к изображению входной:

(2.4)

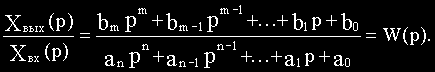
Отношение изображения выходной величины элемента (или системы) к изображению его входной величины при нулевых начальных условиях называется передаточной функцией элемента (или системы).

Передаточная функция W(p) является дробно-рациональной функцией комплексной переменной р:

Из определения передаточной функции следует, что:

Передаточная функция является основной формой математического описания объектов в теории автоматического управления и так как она полностью определяет динамические свойства объекта, то первоначальная задача расчета САУ сводится к определению передаточной функции.

Рассмотрим примеры по определению передаточной функций некоторых простейших схем, характерных для электроники.

Пример 2.1. Вывести передаточную функцию для схемы на рис.2.2, считая входным воздействием приложенное напряжение u, а выходным — ток в цепи i.

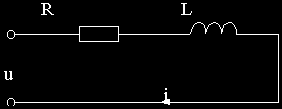
Рис.2.2

Процессы в схеме описываются уравнением:

Перейдем к изображениям по Лапласу:

Составим передаточную функцию как отношение изображения выходной величины к изображению входной величины:

где k=1/R— коэффициент передачи,

T=L/R — постоянная времени.

Передаточные функции принято записывать в такой форме, чтобы свободные члены полиномов от р равнялись бы единице, что и сделано как в рассмотренном примере, так и в последующих.

Пример 2.2. Вывести передаточную функцию схемы на рис.2.3, считая входной величиной напряжение u₁, а выходной — u₂.

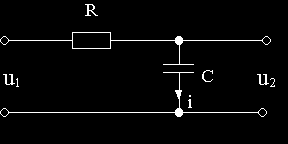
Рис.2.3

При выводе передаточной функции будем считать, что цепочка не нагружена (никаких элементов к выходным зажимам не подключено, либо эти элементы имеют сопротивление, стремящееся к бесконечности) и сопротивление источника входного напряжения настолько велико, что его можно считать равным бесконечности.

Подставим (в) в (а):

Перейдем к изображениям:

где T=RC— постоянная времени.

Пример 2.3. Вывести передаточную функцию схемы на рис.2.4, считая входной величиной u₁, выходной u₂, при допущениях, сформулированных в примере 2.2. i_C

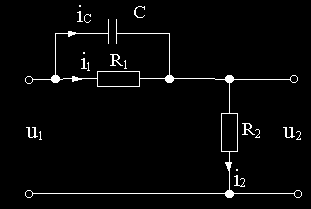
Рис.2.4

Составляем два уравнения по второму закону Кирхгофа, одно уравнение по первому закону Кирхгофа и расписываем выходную величину:

Из уравнений (б) и (в) соответственно получим:

Подставим полученные выражения i₁(t) и i₂(t) в уравнения (а) и (г):

Перейдем к изображениям:

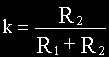
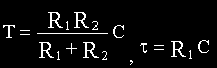
где — коэффициент передачи,

— постоянные времени.

Пример 2.4. Вывести передаточную функцию схемы на рис.2.5, считая входной величиной u₁, выходной — u₂, при допущениях, сформулированных в примере 2.2.

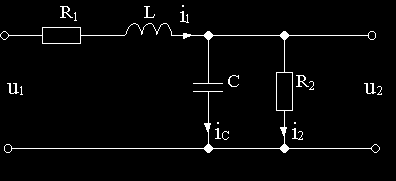
Рис.2.5

Система уравнений электрического равновесия схемы для мгновенных значений величин:

Последнее соотношение здесь, конечно, не уравнение, а обозначение выходной величины.

Уравнения в операторной форме:

Подставим полученное значение I₂(p) в (в):

Последнее соотношение подставим в (а) и определим передаточную функцию:

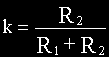
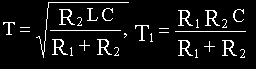
где — коэффициент передачи,

— постоянные времени.

Пример 2.5. Вывести передаточную функцию схемы на рис.2.6, а , содержащей операционный усилитель.

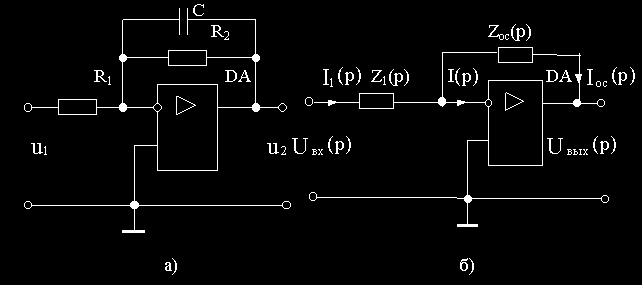
Рис.2.6

Операционными усилителями называются усилители постоянного тока малой мощности с большим коэффициентом усиления. В настоящее время они выполняются по интегральной технологии, т.е. в виде микросхем.

Выведем вначале передаточную функцию для типового включения операционного усилителя, показанного на рис.2.6, б, в общем виде.

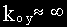
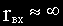
Так как реальные микросхемы операционных усилителей имеют большой коэффициент усиления k_оу и большое входное сопротивление r_вх, то предположим, что и .

С учетом принятых допущений напряжение между инвертирующим и неинвертирующим входами операционного усилителя

Отсюда следует, что напряжение на входе “-“ (инвертирующем) и тогда

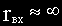
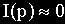
Кроме того, учитывая, что , можно считать и, следовательно

Выходное напряжение схемы тогда определяется следующим соотношением:

Теперь легко получить выражение для передаточной функции схемы (см.рис.2.6, б):

(2.5)

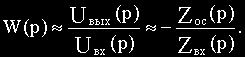
Знак “минус” в последнем выражении указывает на то, что полярность выходного напряжения схемы противоположна полярности входного напряжения.

Для определения передаточной функции схемы на рис.2.6, а вначале найдем сопротивление конденсатора Z_C(p) в операторной форме.

Мгновенное значение тока через емкость равно:

Переходя к изображениям по Лапласу:

Из последнего равенства

(Аналогично для индуктивности можно получить Z_L(p)=Lp).

Используя выведенное значение Z_C(p), для схемы на рис.2.6, а получим:

Z₁(p)=R₁;

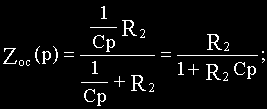
где k=R₂/R₁— коэффициент передачи,

T=R₂C- постоянная времени.

2.2. Частотные характеристики

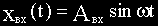
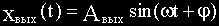
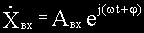
Если на вход линейной непрерывной системы (или отдельного звена) подать синусоидальные (гармонические) колебания с постоянными амплитудой и частотной , то после затухания переходных процессов на выходе также возникают синусоидальные колебания с той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний. Как известно из курса «Основы теории цепей, часть 1», синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд. Комплексные амплитуды рассматриваемых здесь входных и выходных колебаний можно записать как и

Подавая на вход системы гармонические колебания с постоянной амплитудой, но различными частотами, на выходе системы тоже получаем гармонические колебания с теми же частотами, но различными амплитудами и фазами относительно входных колебаний.

Введем в рассмотрение отношение комплексных амплитуд выходных и входных колебаний:

(2.6)

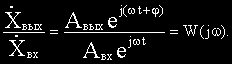
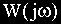
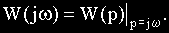
Функция называется комплексной частотной и получается чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции переменной р на переменную :

(2.7)

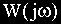
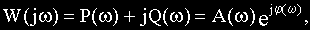
В различных формах записи функцию можно представить в следующем виде:

(2.8)

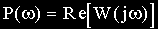
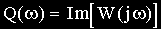
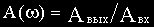
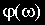
где и — действительная и мнимая части комплексной частотной функции,

и — модуль и аргумент комплексной частотной функции.

При фиксированном значении частоты 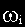комплексную частотную функцию можно изобразить вектором на комплексной плоскости, как показано на рис.2.7.

Изменение частоты приведет к изменению величины и расположения вектора на комплексной плоскости, а конец вектора опишет некоторую траекторию. Геометрическое место концов векторов комплексной частотной функции при изменении частоты от нуля до бесконечности называется амплитудно-фазовой частотной характеристикой (АФЧХ).

В свою очередь все величины, представленные в (2.8), являются соответствующими частотными функциями, а построенные по выражениям для функций графики — частотными характеристиками.

называется вещественной частотной, а — мнимой частотной характеристикой.

показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется амплитудной частотной характеристикой.

показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется фазовой частотной характеристикой.

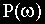
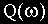
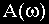
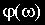
Между всеми частотными характеристиками существует непосредственная связь, вытекающая из тригонометрических соотношений и поясняемая рис.2.7.

В практических расчетах чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе, что позволяет в значительной степени сократить объем вычислительных работ.

Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство при выражении десятичным логарифмом величины отношения мощности на входе P_вых к мощности на входе P_вх в технике принят бел. Так как мощность сигнала пропорциональна его амплитуде, получим:

Но так как бел является достаточно крупной единицей усиления (ослабления) мощности (увеличению мощности в 10 раз соответствует 1 Б), то за единицу измерения ее принят децибел 1дБ=0,1 Б.

С учетом этого можно записать:

Величина логарифма амплитудной частотной характеристики, выраженная в децибелах

называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ).

Таким образом, изменению отношения двух амплитуд в 10 раз соответствует изменение усиления на 20 дБ, в 100 раз — на 40 дБ, в 1000 раз — на 60 дБ и т.д.

Вычислим, какому отношению амплитуд соответствует один децибел, два и т.д.

То есть 1 дБ 1,222.

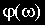
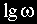
Фазовая частотная характеристика , построенная в полулогарифмическом масштабе (в координатах: угол в градусах или радианах и ), называется логарифмической фазовой частотной характеристикой (ЛФЧХ).

За единицу измерения частоты используется логарифмическая единица декада. Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением.

В логарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную

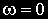
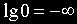
ЛАЧХ и ЛФЧХ строят обычно совместно, используя общую ось абсцисс (ось частот). Начало координат невозможно взять в точке , так как . Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот.

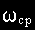
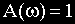
Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза . Ось абсцисс соответствует значению , то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства).

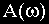
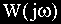
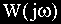
Из рассмотренных здесь частотных характеристик две можно получить экспериментально-амплитудную и фазовую W_oc(p). Из этих двух экспериментальных остальные частотные характеристики могут быть рассчитаны по соответствующим формулам, например — по формуле (2.8). Кроме того, рассчитав по экспериментальным данным , по (2.7) путем обратной подстановки (заменив на р) можно получить передаточную функцию, по (2.4) — из передаточной функции дифференциальное уравнение в операторной форме и далее, применив обратное преобразование Лапласа — дифференциальное уравнение (уравнение динамики системы).

2.3. Временные функции и характеристики

Под временными характеристиками в общем случае понимается графическое изображение процесса изменения выходной величины в функции времени при переходе системы из одного равновесного состояния в другое в результате поступления на вход системы некоторого типового воздействия.

Так как дифференциальное уравнение системы тоже определяет изменение выходной величины в функции времени при некоторых начальных условиях, то временная характеристика изображает собой решение дифференциального уравнения для принятого типового воздействия и, следовательно. полностью характеризует динамические свойства системы.

Так как временные характеристики могут быть получены не только путем решения дифференциального уравнения, но и экспериментально, то возможность определения динамических свойств системы по временной характеристике имеет исключительно важное практическое значение, поскольку в этом случае не требуется выводить и решать дифференциальное уравнение.

В качестве типовых воздействий наиболее широкое применение находят единичное ступенчатое и единичное импульсное воздействия.

Математическое выражение единичного ступенчатого воздействия может быть записано в виде

Под единичным импульсным воздействием понимается предельно короткий импульс

площадь которого равна единице, то есть

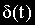
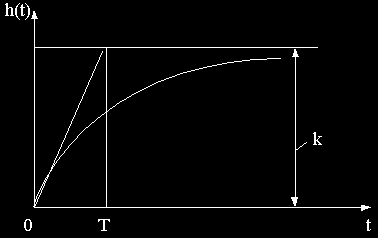
Выражение для единичного импульса в математике принято называть дельта-функцией.

Графическое изображение реакции системы на единичное ступенчатое воздействие называется переходной характеристикой.

Аналитическое выражение переходной характеристики обозначается h(t) и называется переходной функцией.

Графическое изображение реакции системы на единичное импульсное воздействие называется импульсной переходной характеристикой.

Аналитическое выражение импульсной переходной характеристики обозначается 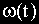и называется импульсной переходной функцией или весовой функцией (функцией веса).

При практических расчетах наиболее широкое применение находит временная характеристика в виде переходной характеристики, так как ее достаточно просто получить экспериментально и, кроме того, определяемый ею переходный процесс часто возникает при включениях и изменениях задающего воздействия.

При поступлении на вход системы с передаточной функцией W(p) величины x_вх(t)=1(t) на выходе получаем переходную характеристику x_вых(t)=h(t).

В преобразованном по Лапласу виде входная и выходная величины запишутся

С учетом этих соотношений получим:

(2.9)

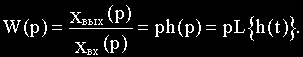
Из последнего выражения следует, что по переходной функции можно получить передаточную функцию.

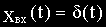
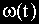
При поступлении на вход САР величины на выходе получаем импульсную переходную характеристику или в преобразованном по Лапласу виде:

В результате определим:

(2.10)

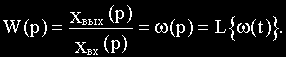
Установим связь между переходной и импульсной переходной функциями, приравняв правые части выражений (2.9) и (2.10):

Но так как р соответствует символу дифференцирования, то

Импульсная переходная функция является производной от переходной функции.

2.4. Структурные схемы и их преобразование

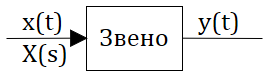
В теории автоматического управления под структурной схемой понимается графическое изображение математического описания. То есть для составления структурной схемы система дробится на элементы, каждый из которых описывается простейшим математическим выражением ( в виде передаточной функции). Структурные схемы содержат следующие четыре типа элементов: звенья направленного действия; устройства сравнения, или сумматоры; линии связи; точки разветвления (узлы).

Звенья направленного действия изображаются прямоугольниками, внутри которых записываются их передаточные функции.

Между собой звенья соединяются с помощью линий связи. На этих линиях стрелками указывается направление распространения сигналов. Следует подчеркнуть, что в направлениях, противоположных указанным стрелками, сигналы не распространяются. Сами линии связи, также как и сумматоры, считаются идеальными, то есть никакими параметрами не обладают.

Сумматоры предназначены для суммирования сигналов (с учетом знака сигнала), как и на функциональных схемах.

Для распределения сигналов по различным направлениям используются узлы, которые обозначаются точками в местах пересечения линий связи.

Для удобства расчетов бывает необходимо преобразовать исходную структурную схему системы к какому-либо желаемому виду, чаще всего — к цепи последовательно соединенных звеньев. В связи с этим рассмотрим основные правила преобразования структурных схем.

При последовательном соединении n звеньев с передаточными функциями W_i(p) эквивалентная передаточная функция W_э(p) определяется их произведением:

При параллельном соединении n звеньев эквивалентная передаточная функция определяется суммой передаточных функций W_i(p) отдельных звеньев:

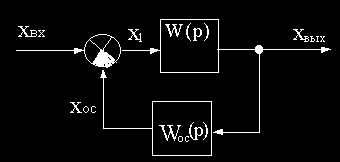
Для случая обратной связи при выводе эквивалентной передаточной функции замкнутого участка W_з(p) используем обозначения, приведенные на рис.2.8.

Схема замкнутого участка системы

Обратная связь называется отрицательной, если

как показано на схеме, и положительно, если

В случае отрицательной обратной связи в изображениях по Лапласу с учетом указанных направлений распространения сигналов запишем:

Отсюда получаем передаточную функцию

Для положительной обратной связи в знаменателе формулы знак «плюс» меняется на «минус».

Указанные три вида преобразования структурных схем являются наиболее часто встречающимися. Для остальных случаев сформулируем основной принцип преобразования и поясним несколькими примерами. При преобразовании структурной схемы передача сигнала по выбранному направлению не должна меняться.

Например, в структурной схеме на рис.2.9, а необходимо перенести узел через звено с передаточной функцией W₂(p).

Преобразование структурной схемы

Чтобы передача сигнала по цепи обратной связи не изменилась, необходимо ввести фиктивное звено с передаточной функцией 1/W₂(p), как показано на рис.2.9, б.

В более сложных случаях в процессе преобразования необходимо производить определенные расчеты.

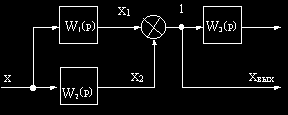
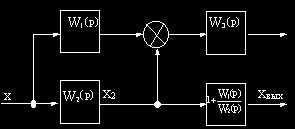
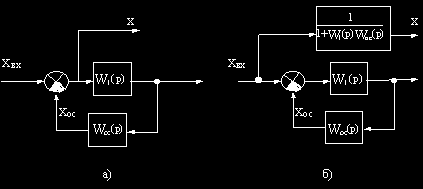
Например, в схеме на рис.2.10, а узел 1 необходимо перенести на выход звена с передаточной функцией W₂(p).

Преобразование структурной схемы

Установим связь между величинами X_вых(p) и X₂(p).

На входе звеньев с передаточными функциями W₁(p) и W₂(p) действует сигнал

На выходе звена с передаточной функцией W₁(p)

На выходе сумматора в узле 1

Отсюда видно, что в рассматриваемом примере при переносе узла необходимо ввести фиктивное звено с передаточной функцией 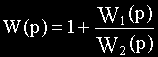, как показано на рис. 2.10, б.

При переносе узла в схеме на рис.2.11, а с выхода сумматора на его положительный вход найдем передаточную функцию фиктивного звена без дополнительных пояснений.

2.5. Типовые звенья и их характеристики

В общем случае какой-либо объект в теории автоматического управления описывается передаточной функцией, содержащей полиномы от р произвольного порядка в числителе и знаменателе. Но если передаточная функция объекта содержит только простой множитель в числителе (знаменатель при этом представляет собой действительное число) либо только простой множитель в знаменателе (числитель представляет собой действительное число), то объект называется типовым динамическим звеном (или просто типовым звеном).

Из курса алгебры известно, что полином любого порядка можно разложить на простые множители. То есть любую САУ можно представить в виде последовательного соединения типовых звеньев. С другой стороны, реальные звенья САУ могут иметь самую разнообразную физическую основу (электронные, механические, гидравлические, электромеханические и т.п.) и конструктивное выполнение, но иметь одинаковые передаточные функции и являться одинаковыми типовыми звеньями. Поэтому знание характеристик звеньев столь же необходимо для расчетов САУ, как знание таблицы умножения в арифметике.

Все линейные типовые звенья разделяют на три группы: позиционные звенья, интегрирующие и дифференцирующие. Позиционные звенья: апериодическое, пропорциональное, колебательное, консервативное и чистого запаздывания — характеризуется тем, что в каждом из них, кроме консервативного, при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины.

В звеньях, относящихся к группе интегрирующих, при постоянном входном воздействии выходная величина неограниченно растет.

Дифференцирующие звенья характеризуются тем, что реагируют только на изменение входной величины.

Рассмотрим типовые звенья и их характеристики.

Пропорциональное (безинерционное) звено. Описывается уравнением и имеет передаточную функцию:

Параметр k называется в общем случае коэффициентом передачи звена и может иметь любую размерность. В частных случаях, когда k является величиной безразмерной, принято пользоваться термином «коэффициент усиления».

Частные и временные функции звена:

Примерами таких звеньев могут служить механические связи, электронные усилители сигналов на низких частотах и др.

Схема на рис.2.6, б, если Z₁(p)=R₁ и Z_oc(p)=R_oc, также будет являться пропорциональным звеном.

Интегрирующее (идеальное) звено.

Уравнение и передаточная функция звена:

или

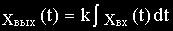
В случае интегрирующего звена параметр k является коэффициентом передачи звена по скорости, численно равным скорости изменения выходной величины при единичном значении входной величины.

Частотные и временные функции звена:

Построенные по указанным функциям характеристики звена представлены на рис.2.12.

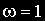
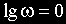
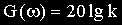
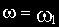
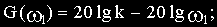
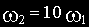
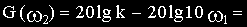
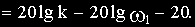
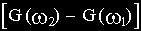
При построении ЛАЧХ удобно отложить точку с координатами (при этом ); и провести прямую с наклоном минус 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ уменьшается на 20 дБ. (При каком-то значении получаем при увеличении частоты на одну декаду, т.е. при , соответственно
Разность этих ординат составляет минус 20 дБ).

В качестве примера элемента, характеристики которого приближенно соответствуют характеристикам идеального интегрирующего звена, можно назвать двигатель постоянного тока с независимым возбуждением и малой электромеханической инерцией. Входной величиной для него является напряжение на зажимах якоря, а выходной — угол поворота вала.

Схема на рис.2.6, б будет являться интегрирующим звеном, если Z₁(p)=R₁, а цепь обратной связи организована конденсатором, т.е.

На самом деле, согласно формуле (2.5) передаточная функция схемы будет

При использовании в рассматриваемой схеме реального операционного усилителя переходная характеристика не может иметь значения, превышающие напряжение питания . Но если предположить операционный усилитель идеальным, то и реализованное здесь интегрирующее звено будет идеальным.

Дифференцирующее (идеальное) звено.

Уравнение и передаточная функции звена:

W(p)=kp.

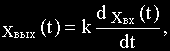
Выходная величина пропорциональна скорости изменения входной величины.

Если входная и выходная величины имеют одинаковую размерность, то коэффициент k измеряется в секундах. В этом случае его принято обозначать через Т и называть постоянной времени дифференцирующего звена.

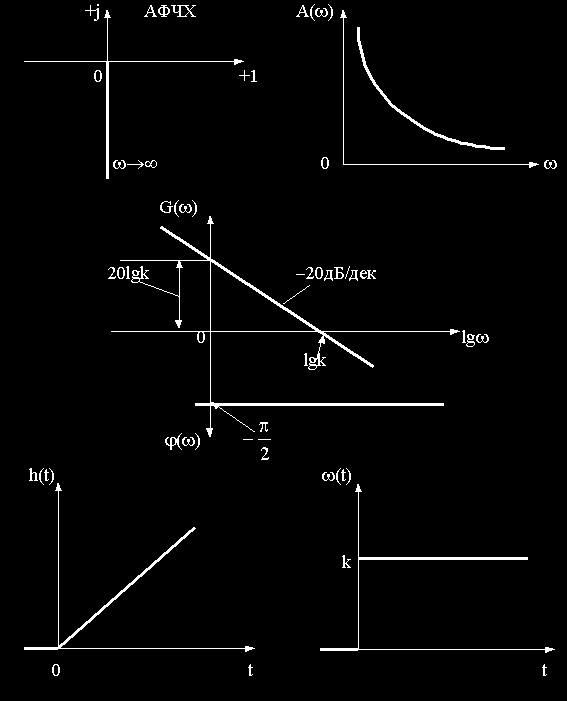
Выражение для основных функций:

Как передаточная функция, так соответственно и частотные характеристики дифференцирующего звена обратны передаточной функции и соответствующим характеристикам интегрирующего звена.

О том, что звено с представленным математическим описанием является идеальным, говорит, к примеру, переходная функция. Ни в каком реальном устройстве невозможно получить скачек выходной величины бесконечной амплитуды.

Реальные дифференцирующие звенья обладают конечной инерционностью, вследствии чего осуществляемое ими дифференцирование не является точным. Примером может служить тахогенератор, если за его входную величину принять угол поворота его вала, а за выходную величину — выходное напряжение. Последнее пропорционально угловой скорости вращения вала, которая в свою очередь равна производной от угла поворота.

Логарифмические частотные характеристики рассматриваемого звена приведены на рис.2.13.

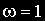
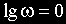
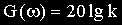
При построении ЛАЧХ удобно отложить точку с координатами (при этом); и провести через нее прямую с наклоном плюс 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ увеличивается на 20 дБ.

Апериодическое (первого порядка) звено. Описывается дифференциальным уравнением

Перейдя к изображениям, получим:

Передаточные и частотные функции:

ЛАЧХ звена показана на рис.2.14. Но эта же характеристика может быть представлена приближенно ломаной линией, которая показана на том же рисунке. Эта приближенная характеристика называется асимптотической ЛАЧХ. Такое название связано с тем, что эта характеристика составлена из двух асимптот, к которым стремится ЛАЧХ при и .

При малых значениях можно считать , то есть , следовательно

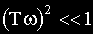
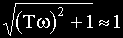
Соответственно характеристика представляет собой прямую, параллельную оси абсцисс и проходящую на уровне 20lgk. Это есть первая асимптота, к которой стремится ЛАЧХ при.

С другой стороны, на больших частотах

В этом случае характеристика представляет собой прямую, имеющую наклон минус 20 дБ/дек. Действительно, при увеличении на декаду, т.е. в 10 раз,

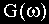
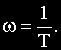
Таким образом, величина уменьшилась на 20lg10, т.е. на 20 дБ. Эта линия является асимптотой, к которой стремится ЛАЧХ при . Обе асимптоты пересекаются в точке, соответствующей частоте Поэтому эта частота называется сопрягающей частотой.

Максимальное расхождение между точной (G_Т) и асимптотической (G_a) ЛАЧХ наблюдается при частоте, равной сопрягающей.

Вычислим это расхождение, подставив в соотношения для G_T и G_a значения сопрягающей частоты :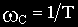

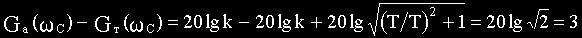
дБ.

От параметров звена рассматриваемая величина не зависит.

На этом же рисунке показана и ЛФЧХ: при значение изменяется от 0 до минус . При этом в точке имеем .

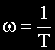
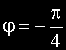
АФЧХ представляет собой полуокружность с радиусом в четвертом квадранте комплексной плоскости и центром в точке (, j0) на действительной оси.

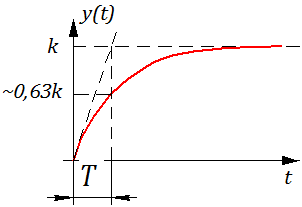
Переходная функция, согласно решению уравнения звена, при x_вх=1(t) и нулевых начальных условиях имеет вид

а импульсная переходная функция

Переходная характеристика представлена на рис.2.15.

Динамические свойства звена характеризуются постоянной времени Т. Постоянная времени может быть определена как время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени.

Коэффициент передачи k определяет свойства звена в установившемся режиме.

Очевидно, имея в распоряжении частотные либо переходные характеристики, полученные, например, экспериментально, можно восстановить передаточную функцию звена.

В рассмотренных выше примерах по определению передаточных функций схемы на рис.2.2; рис.2.3; рис.2.6, а являются апериодическими звеньями.

Асимптотическая ЛАЧХ апериодического звена имеет частоту среза 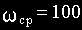. Коэффициент передачи звена k=10. Требуется определить постоянную времени Т.

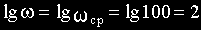
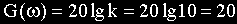
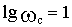
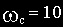
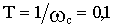
Нужно на графике или мысленно провести из точки на оси частот прямую с наклоном минус 20 дБ/дек до пересечения с горизонталью, проведенной на уровне . Координата точки пересечения по оси частот даст логарифм сопрягающей частоты , отсюда и с.

Звенья второго порядка. В общем случае описываются уравнением

Перейдем к изображениям по Лапласу:

Отсюда определяем передаточную функцию:

Однако общепринята запись передаточной функции звеньев второго порядка в другом виде:

где

Звенья второго порядка, таким образом, характеризуются тремя параметрами. Это коэффициент передачи. постоянная времени и коэффициент демпфирования . В зависимости от величины коэффициента демпфирования различают типы звеньев: колебательное (0 1 параметры k и Т будут отрицательны, но если умножить и числитель, и знаменатель выведенной передаточной функции на минус единицу, то получим записанную выше передаточную функцию неминимально-фазового звена.

Эта передаточная функция имеет положительный полюс p₁=1/T.

Частотные характеристики такого звена:

Но для обычного апериодического звена имеем:

Разница между ними. как видим, в величине фазы. Амплитудные же характеристики одинаковы. Оказывается, что из всех возможных звеньев с одинаковыми амплитудными характеристиками обычные типовые звенья обладают наименьшими по абсолютному значению фазовыми характеристиками. В этом и состоит смысл введенных терминов.

Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудной характеристике можно определить фазовую и наоборот.

2.7. Частотные характеристики разомкнутых систем

Так как полиномы произвольного порядка можно разложить на простые множители, то любую передаточную функцию можно представить в виде произведений простых множителей в числителе и знаменателе или. другими словами, в виде цепочки последовательно соединенных типовых динамических звеньев. Для такой цепочки звеньев (т.е. для разомкнутой однокортнутой системы) передаточная и комплексная частотная функции запишутся в виде:

где W_i(p) и W_i(jω )— передаточные и комплексные частотные функции типовых динамических звеньев.

В этом случае модули и аргументы комплексных функций звеньев и системы связываются следующими соотношениями:

Отсюда вытекает правило построения ЛАЧХ и ЛФЧХ разомкнутой одноконтурной САУ: строят логарифмические характеристики звеньев и затем их графически складывают.

Но для построения асимптотической ЛАЧХ применяют более простой метод, который сформулируем после рассмотрения численного примера.

Пример 2.8. Построить асимптотическую ЛАЧХ для разомкнутой системы с передаточной функцией

По виду передаточной функции можно заключить, что система состоит из последовательно соединенных n интегрирующих, форсирующего. апериодического и колебательного звеньев.

Рассчитаем сопрягающие частоты (, а в каждом простом множителе в числителе и знаменателе передаточной функции присутствует Tp):

ω ₁ сопрягающая частота апериодического звена,

ω ₂— сопрягающая частота форсирующего звена,

ω ₃— сопрягающая частота колебательного звена.

Примем для определенности n=1. Кроме того, будем считать, что коэффициент передачи интегрирующего звена равен коэффициенту передачи разомкнутой САУ, а коэффициенты передачи всех остальных звеньев равны единице.

Определим величину 20lgk : 20lg30=29.

Характеристики звеньев построены на рис.2.18, где соответственно ломаные линии 1,2,3, 4 являются ЛАЧХ интегрирующего, апериодического, форсирующего и колебательного звеньев. Так как коэффициенты передачи всех звеньев, кроме интегрирующего, приняты единичными, то ЛАЧХ этих звеньев при совпадают с осью частот.

Пример построения асимптотической ЛАЧХ

Просуммировав графически ЛАЧХ всех звеньев, получим характеристику 5, являющуюся ЛАЧХ разомкнутой системы.

Из этого примера видно, что суммарную характеристику легко можно построить, не изображая характеристик отдельных звеньев.

Поэтому при построении ЛАЧХ разомкнутых САУ (или цепи последовательно соединенных звеньев) вначале проводят первую асимптоту через точку с координатами с наклоном минус n*20дБ/дек, где n равно разности между числами идеальных интегрирующих и дифференцирующих звеньев. После каждой сопрягающей частоты наклон ЛАЧХ изменяют, причем изменение наклона определяется типом звена, давшим сопрягающую частоту. Причем если у колебательного звена -3 c

Параметры асимптотической ЛАЧХ:

При построении ЛАЧХ откладываем точку с координатами и проводим через нее прямую с наклоном плюс 20 дБ/дек до сопрягающей частоты. После сопрягающей частоты наклон ЛАЧХ изменяется на минус 20дБ/дек, т.е. вторая асимптота идет горизонтально. Характеристика представлена на рис.2.22.

Рассмотренные здесь схемы зачастую называют инерционным форсирующим и инерционным дифференцирующим звеньями (или реальными форсирующим и дифференцирующим звеньями).