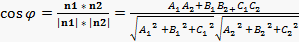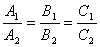Переход от общего уравнения прямой к другим видам уравнения прямой и обратно.
Существуют различные виды уравнения прямой на плоскости, описывающие одну и ту же линию. В зависимости от условий задачи удобно использовать тот или иной вид уравнения прямой. Поэтому, полезно уметь переходить от уравнения прямой одного вида к уравнению прямой другого вида. Цель этого пункта статьи заключается в приобретении навыков приведения общего уравнения прямой к другим видам уравнения прямой и обратно.
Начнем с приведения общего уравнения прямой 

Если 


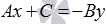


Если 

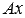
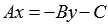


Запоминать полученные формулы не имеет смысла, проще повторять указанные действия при приведении общего уравнения прямой к каноническому виду.
Плоскость в пространстве
Общее уравнение плоскости; его частные случаи.
Каждую плоскость в пространстве можно представить как линейное уравнение, называемое общим уравнением плоскости

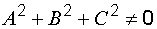
Коэффициенты 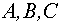


Частные случаи.
1. Если в уравнении (8) 
2. Если С=0, то имеем ур-е: Аx+By+D=0. Нормальный вектор n=(A,B,0) перпендикулярен оси Оz. Следовательно плоскость параллельна оси Оz, если В=0 – параллельна оси Оy, А=0 – параллельна оси Оx.
3. Если С=D=0, то плоскость проходит через О(0;0;0) параллельно оси Оz, т.е. плоскость Аx+By=0 проходит через ось Оz. Аналогично ур-ям Ву+Сz=0 и Ах+Сz=0 отвечают плоскости, порходящие соответственно через ос Ох и Оу.
4. Если А=В=0, то ур-е (8) принимает вид Сz+D=0, т.е. z= -D/C. Плоскость параллельна плоскости Оху. Аналогично ур-ям Ах+D=0 и Ву+D=0 отвечают плоскости, соответственно параллельные плоскостям Оух и Охz.
5. Если А=В=D=0, то ур-е (8) примет вид Сz=0, т.е. z=0. Это ур-е плоскости Оху. Аналогично у=0 – ур-е плоскости Охz, х=0 – ур-е плоскости Оуz.
Угол между двумя плоскостями; условия параллельности и перпендикулярности плоскостей
Угол между плоскостями. Угол φ между нормальными векторами n1 и n2 двух плоскостей является углом между плоскостями.
Условия перпендикулярности 2х плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, 

Таким образом, 
3) Условия параллельности 2х плоскостей.Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы 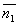

- Общее уравнение прямой: описание, примеры, решение задач
- Общее уравнение прямой: основные сведения
- Неполное уравнение общей прямой
- Общее уравнение прямой, проходящей через заданную точку плоскости
- Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
- Составление общего уравнения прямой
- Способы задавания уравнений прямых в плоскости и в трехмерном пространстве
- Определение прямой и виды уравнений для ее описания
- Векторное и параметрическое описание прямой
- Общее уравнение
- Уравнение в отрезках и каноническое
- Задача на построение уравнения прямой
- Задача на определение точки пересечения прямых
- 💥 Видео
Видео:11. Прямая в пространстве и ее уравненияСкачать

Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0
Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
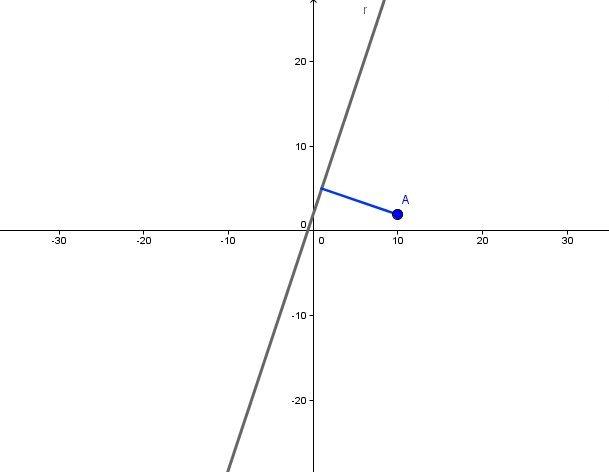
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0
Ответ: 7 x — 2 = 0
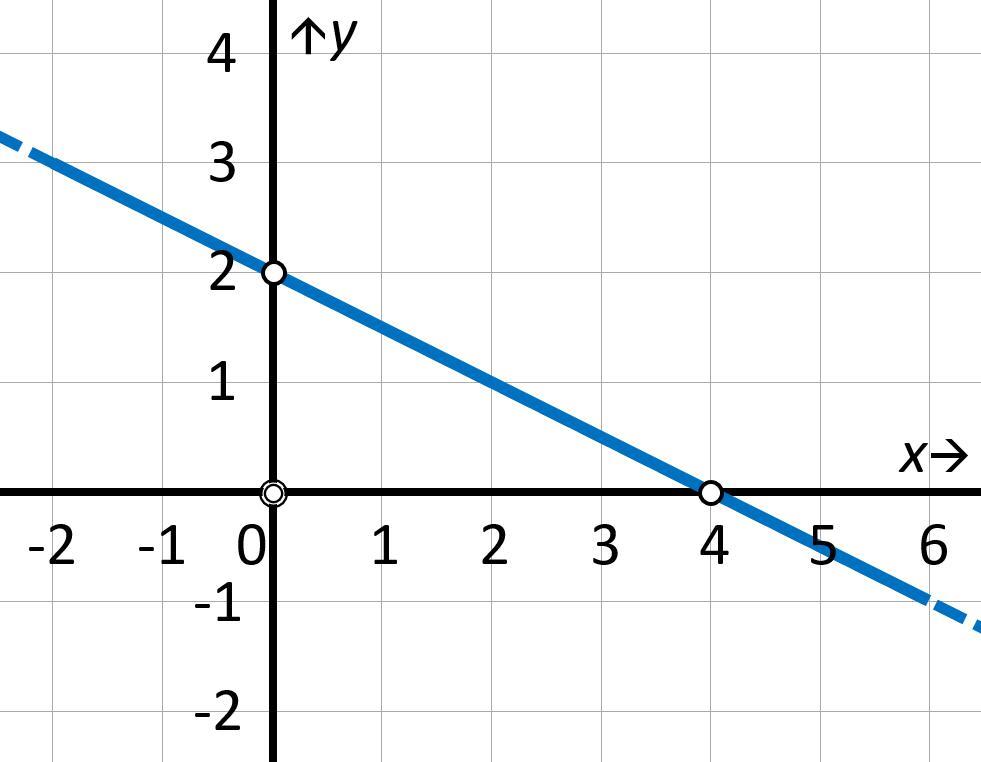
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .
Ответ: y — 3 = 0 .
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .
Ответ: x — 2 · y + 11 = 0 .
Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 — y 0 — 1 2 = 0
Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2
Ответ: — 5 2
Видео:Видеоурок "Канонические уравнения прямой"Скачать

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .
Это равенство возможно записать как пропорцию: x + C A — B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .
Перепишем равенство в виде пропорции: x — B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .
Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x — 3 = y — 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x
Ответ: y = — 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Ответ: x — 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0
Перейдем от канонического к общему:
x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0
Ответ: y — 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0
Ответ: 1 3 x + 2 y — 1 = 0 .
Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0
Ответ: 2 x — 3 y — 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Способы задавания уравнений прямых в плоскости и в трехмерном пространстве
Прямая является основным геометрическим объектом на плоскости и в трехмерном пространстве. Именно из прямых строятся многие фигуры, например: параллелограмм, треугольник, призма, пирамида и так далее. Рассмотрим в статье различные способы задавания уравнений прямых.
Видео:Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Определение прямой и виды уравнений для ее описания
Каждый школьник хорошо себе представляет, о каком геометрическом объекте идет речь. Прямую можно представить как совокупность точек, причем если соединить каждую из них по очереди со всеми остальными, то мы получим набор параллельных векторов. Иными словами, попасть в каждую точку прямой можно из одной фиксированной ее точки, перенося ее на некоторый единичный вектор, умноженный на действительное число. Это определение прямой используется для задавания векторного равенства для ее математического описания как на плоскости, так и в трехмерном пространстве.

Прямая может быть математически представлена следующими видами уравнений:
- общее;
- векторное;
- параметрическое;
- в отрезках;
- симметричное (каноническое).
Далее рассмотрим все названные виды и покажем на примерах решения задач, как с ними работать.
Видео:Лекция 28. Виды уравнения прямой в пространстве.Скачать

Векторное и параметрическое описание прямой

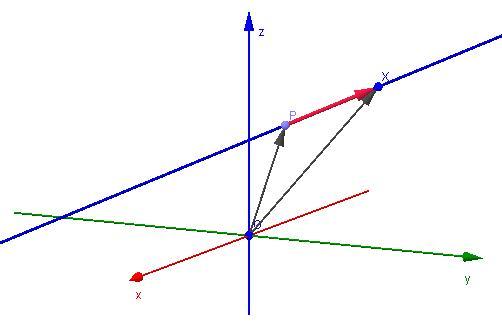
Начнем с задавания прямой через известный вектор. Предположим, что в пространстве имеется фиксированная точка M(x0; y0; z0). Известно, что прямая проходит через нее и направлена вдоль векторного отрезка v¯(a; b; c). Как по этим данным найти произвольную точку прямой? Ответ на этот вопрос даст следующее равенство:
(x; y; z) = (x0; y0; z0) + λ * (a; b; c)
Где λ — произвольное число.
Аналогичное выражение можно записать для двумерного случая, где координаты векторов и точек представлены набором из двух чисел:
(x; y) = (x0; y0) + λ * (a; b)
Записанные уравнения называются векторными, а сам направленный отрезок v¯ — это направляющий вектор для прямой.
Из записанных выражений соответствующие параметрические уравнения получаются просто, достаточно лишь переписать их в явном виде. Например, для случая в пространстве получаем следующее уравнение:
С параметрическими уравнениями удобно работать, если необходимо проанализировать поведение каждой координаты. Заметим, что хотя параметр λ может принимать произвольные значения, но во всех трех равенствах он должен быть одинаковым.
Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Общее уравнение
Другим способом задавания прямой, который часто используют для работы с рассматриваемым геометрическим объектом, является применение уравнения общего вида. Для двумерного случая оно имеет вид:
A * x + B * y + C = 0
Здесь большие латинские буквы представляют конкретные числовые значения. Удобство данного равенства при решении задач заключается в том, что оно в явном виде содержит вектор, который перпендикулярен прямой. Если обозначить его n¯, тогда можно записать:
Кроме того, выражение удобно применять для определения расстояния от прямой до некоторой точки P(x1; y1). Формула для расстояния d имеет вид:
d = |A * x1 + B * y1 + C| / √(A2 + B2)
Несложно показать, что если из общего уравнения выразить явно переменную y, то получится следующая известная форма записи прямой:
Где k и b однозначно определяются числами A, B, C.
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Уравнение в отрезках и каноническое
Уравнение в отрезках проще всего получить из общего вида. Покажем, как это можно сделать.
Предположим, что имеется следующая прямая:
A * x + B * y + C = 0
Перенесем свободный член в правую часть равенства, затем поделим на него все уравнение, получаем:
x / (-C / A) + y / (-C / B) = 1;
x / q + y / p = 1, где q = -C / A, p = -C / B
Мы получили так называемое уравнение в отрезках. Свое название оно получило по причине того, что знаменатель, на который делится каждая переменная, показывает значение координаты пересечения прямой с соответствующей осью. Этот факт удобно использовать для изображения прямой в координатной системе, а также для анализа ее взаимного расположения по отношению к другим геометрическим объектам (прямым, точкам).
Теперь перейдем к получению канонического уравнения. Это проще сделать, если рассмотреть параметрический вариант. Для случая на плоскости имеем:
Выразим параметр λ в каждом равенстве, затем приравняем их, получаем:
(x — x0) / a = (y — y0) / b
Это и есть искомое уравнение, записанное в симметричной форме. Так же, как и векторное выражение, оно в явной форме содержит координаты направляющего вектора и координаты одной из точек, которая принадлежит прямой.
Можно заметить, что в данном пункте мы привели уравнения для двумерного случая. Аналогичным образом можно составить уравнение прямой в пространстве. Здесь нужно заметить, что если каноническая форма записи и выражение в отрезках будут иметь такой же вид, то общее уравнение в пространстве для прямой представляется системой из двух уравнений для пересекающихся плоскостей.
Видео:Видеоурок "Общие уравнения прямой"Скачать

Задача на построение уравнения прямой
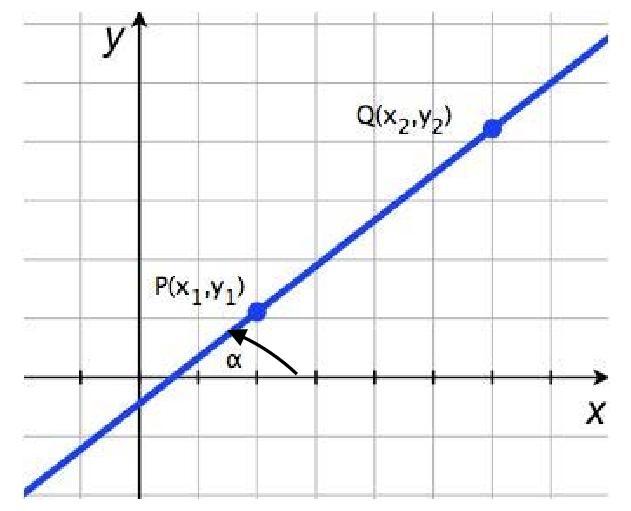
Из геометрии каждый школьник знает, что через две точки можно начертить единственную линию. Предположим, что в координатной плоскости заданы следующие точки:
Следует найти уравнение прямой, которой принадлежат обе точки, в отрезках, в векторном, каноническом и в общем виде.
Получим сначала векторное уравнение. Для этого следует определить для прямой направляющий вектор M1M2¯:
M1M2¯ = (-1; 3) — (1; 2) = (-2; 1)
Теперь можно составить векторное уравнение, взяв одну из двух заданных в условии задачи точек, например, M2:
(x; y) = (-1; 3) + λ * (-2; 1)
Чтобы получить каноническое уравнение, достаточно преобразовать найденное равенство в параметрический вид и исключить параметр λ. Имеем:
x = -1 — 2 * λ, следовательно, λ = x + 1 / (-2);
y = 3 + λ, далее получаем λ = y — 3;
x + 1 / (-2) = (y — 3) / 1
Оставшиеся два уравнения (общее и в отрезках) можно найти из канонического, преобразуя его следующим образом:
общее уравнение: x + 2 * y — 5 = 0;
в отрезках уравнение: x / 5 + y / 2,5 = 1
Полученные уравнения показывают, что вектор (1; 2) должен быть перпендикулярен прямой. Действительно, если найти его скалярное произведение с направляющим вектором, то оно будет равно нулю. Уравнение в отрезках говорит, что прямая пересекает ось x в точке (5; 0), а ось y — в точке (2,5; 0).
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Задача на определение точки пересечения прямых
На плоскости заданы две прямые следующими уравнениями:
(x; y) = (0; -1) + λ * (-1; 3)
Необходимо определить координаты точки, в которой эти прямые пересекаются.
Решить задачу можно двумя способами:
Поступим вторым способом. Имеем:
2 * (-λ) + (-1) + 3 * λ — 1 = 0;
Подставляем полученное число в векторное уравнение:
(x; y) = (0; -1) + 2 * (-1; 3) = (-2; 5)
Таким образом, единственной точкой, которая принадлежит обеим прямым, является точка с координатами (-2; 5). В ней прямые пересекаются.
💥 Видео
Уравнение прямой на плоскостиСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Уравнение прямой по двум точкамСкачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Уравнение прямой.Скачать

Составляем уравнение прямой по точкамСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать