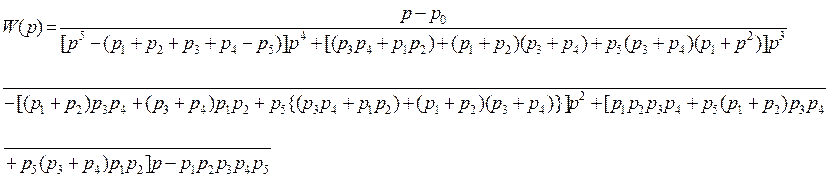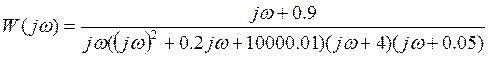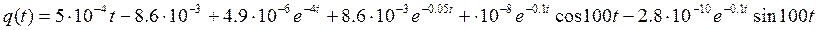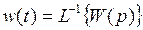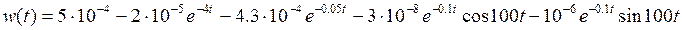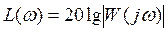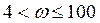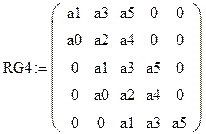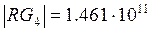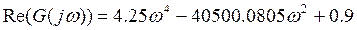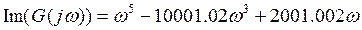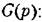Передаточные функции находят широкое применение при исследовании систем автоматического управления. Зная передаточную функцию, можно определить временные и частотные характеристики системы. Кроме того, можно определить и изменение регулируемой величины при приложении к системе воздействий произвольной формы.
В зависимости от того, рассматривается ли поведение системы при задающем или при возмущающем воздействии, различают передаточные функции системы по задающему и по возмущающему воздействиям. При этом различают передаточные функции разомкнутых и замкнутых систем.
Рассмотрим понятие передаточной функции системы по задающему воздействию.
Передаточной функцией системы по задающему воздействию называется отношение изображения по Лапласу выходной величины системы X(p)=L[x(t)] к изображению по Лапласу задающего воздействия G(p)=L[g(t)] при нулевых начальных условиях.
Передаточная функция замкнутой системы по задающему воздействию обозначается через Ф(р) и равна
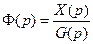
Передаточная функция разомкнутой системы по задающему воздействию обозначается через W(p) и равна
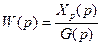
где Xр(p) – изображение по Лапласу выходной величины разомкнутой системы при нулевых начальных условиях.
Передаточной функцией системы по возмущающему воздействию называется отношение изображения по Лапласу выходной величины системы к изображению по Лапласу возмущающего воздействия F(p)=L[f(t)] при нулевых начальных условиях.
Передаточная функция замкнутой системы по возмущающему воздействию обозначается через Ff(p) и равна
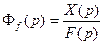
Передаточная функция разомкнутой системы по возмущающему воздействию обозначается через V(p) и равна
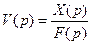
При определении передаточных функций разомкнутых систем имеется в виду, что рассматривается поведение системы, у которой главная отрицательная обратная связь разомкнута.
Кроме рассмотренных выше передаточных функций, при анализе систем автоматического регулирования очень часто используют передаточную функцию замкнутой системы по ошибке.
Передаточной функцией замкнутой системы по сигналу ошибки называется отношение изображения по Лапласу ошибки к изображению по Лапласу задающего воздействия при нулевых начальных условиях. Она равна
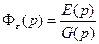
где E(p)=L[e(t)] – изображение по Лапласу ошибки системы при нулевых начальных условиях.
Определим связь между передаточными функциями разомкнутой и замкнутой систем автоматического регулирования. Так как структурная схема любой сложной многоконтурной системы с одной регулируемой величиной методами структурных преобразований может быть приведена к схеме одноконтурной системы, то в общем случае структурная схема САУ может быть представлена так, как изображено на рис.7.5,а. Задающее воздействие g(t) приложено ко входу звена с передаточной функцией W1(p), а возмущающее воздействие f(t) действует на вход звена W2(p). Разомкнем систему, т.е. отключим выход звена W2(p) от сумматора. Структурная схема примет вид, изображенный на рис.7.5,б.
Пользуясь правилом структурных преобразований и применяя принцип суперпозиции, так как САУ является линейной, определим передаточные функции разомкнутой системы.
Передаточная функция разомкнутой системы по задающему воздействию при f(t)=0 будет равна
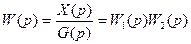
а по возмущающему воздействию при g(t)=0 будет иметь вид
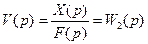
Замкнем систему, т.е. вновь подключим выход звена W2(p) к сумматору (рис.7.5,а).
Рис.7.5. Преобразование структурной схемы САУ
Рассмотрим поведение системы при задающем воздействии и при f(t)=0. Тогда структурная схема САУ примет вид, как показано на рис.7.5,в, а передаточная функция замкнутой системы по задающему воздействию примет вид
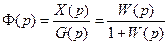
Определим выражение для передаточной функции замкнутой системы по ошибке. Поведение системы рассматривается только при задающем воздействии, а выходной величиной системы является ошибка e (рис.7.5,г). Тогда передаточная функция замкнутой системы по ошибке равна
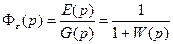
Сравнивая выражения (7.17) и (7.18), можно записать
Полученные выражения (7.17), (7.18) устанавливают связь между передаточной функцией разомкнутой САУ и передаточными функциями замкнутой системы соответственно по задающему воздействию и по сигналу ошибки.
Рассмотрим поведение системы только при возмущающем воздействии, т.е. g(t)=0. Тогда структурная схема системы примет вид, изображенный на рис.7.5,д, а передаточная функция замкнутой системы по возмущающему воздействию будет
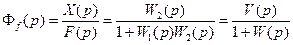
Выражение (7.19) определяет связь между передаточной функцией замкнутой системы по возмущающему воздействию и передаточными функциями разомкнутой системы.
По передаточной функции разомкнутой системы по задающему воздействию можно определить характеристические полиномы и характеристические уравнения системы в разомкнутом и замкнутом состояниях. Передаточная функция W(p) может быть представлена как отношение двух многочленов:
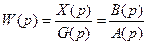
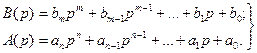
Многочлен 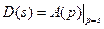
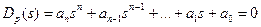
Аналогично может быть получено характеристическое уравнение замкнутой системы. Так как
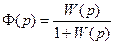
то, подставив выражение (7.20) в (7.23), получим
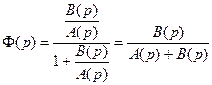
Таким образом, характеристическое уравнение замкнутой системы будет иметь вид:
Выражение (7.26) показывает, что характеристическое уравнение замкнутой системы можно получить по передаточной функции разомкнутой системы. Для этого необходимо просуммировать многочлен числителя и знаменателя передаточной функции W(p), заменить переменную и полученное выражение приравнять к нулю.
Вполне очевидно, что характеристическое уравнение как замкнутой, так и разомкнутой систем имеет одну и ту же степень.
Из выражений (7.17), (7.18) и (7.19) видим, что знаменатели этих выражениий одинаковые. Поэтому характеристическое уравнение замкнутой системы может быть получено по любой из передаточных функций замкнутой системы.
Видео:7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Передаточная функция разомкнутой системы. Передаточная функция замкнутой системы. Дифференциальное уравнение системы
Страницы работы
Фрагмент текста работы
Методические указания к практическим занятиям
Оглавление.
2. Передаточная функция разомкнутой системы……………………. 4
3. Передаточная функция замкнутой системы………………………. 4
4. Дифференциальное уравнение системы…………………………….4
5. Структурная схема замкнутой системы…………………………….5
9. Переходная характеристика…………………………………………9
11. Асимптотическую ЛАЧХ и ЛФЧХ………………………………..11
12. Анализ устойчивости системы методом Рауса – Гурвица……….13
13. Анализ устойчивости системы методом Михайлова…………….14
14. Анализ устойчивости системы методом Найквиста……………..16
15. Анализ устойчивости системы при помощи ЛАЧХ и ЛФЧХ…. 17
16. Запас устойчивости……………………………………………. …20
По заданным нулю и пяти полюсам передаточной функции разомкнутой системы автоматического регулирования выполнить следующие задания:
· Записать функцию разомкнутой системы
· Записать функцию замкнутой системы
· Записать дифференциальное уравнение системы
· Начертить структурную схему замкнутой системы
· Определить АЧХ системы
· Определить ФЧХ системы
· Определить переходную характеристику
· Определить весовую функцию
· Построить асимптотическую ЛАЧХ и ЛФЧХ
· Проанализировать устойчивость системы методом Рауса – Гурвица
· Проанализировать устойчивость системы методом Михайлова
· Проанализировать устойчивость системы методом Найквиста
· Проанализировать устойчивость системы при помощи ЛАЧХ и ЛФЧХ
· Определить запас устойчивости
2. Запишем передаточную функцию разомкнутой системы:
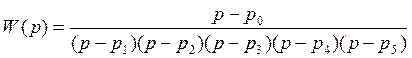
Подставив значения корней и полюсов, получим:
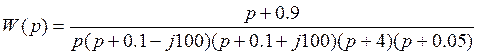
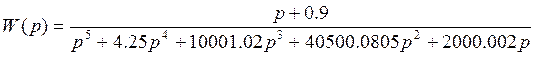
3. Запишем передаточную функцию для замкнутой системы:
Переход от разомкнутой системы к замкнутой осуществим по формуле: 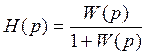
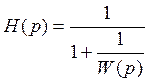
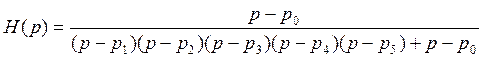
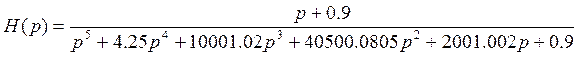
4. Запишем дифференциальное уравнение для замкнутой системы:
Передаточную функцию можно представить как отклик 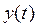
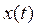
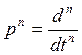
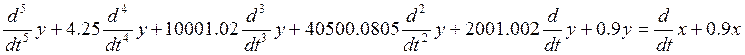
5. Нарисуем структурную схему замкнутой системы:
Структурная схема замкнутой системы представляет собой разомкнутую систему, охваченную отрицательной обратной связью. Разомкнутая система представляет собой каскадное соединение различных звеньев. Учитывая вышесказанное, нарисуем структурную схему замкнутой системы:
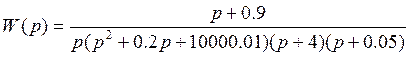
Где 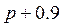
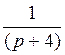
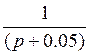
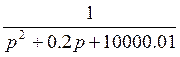
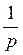
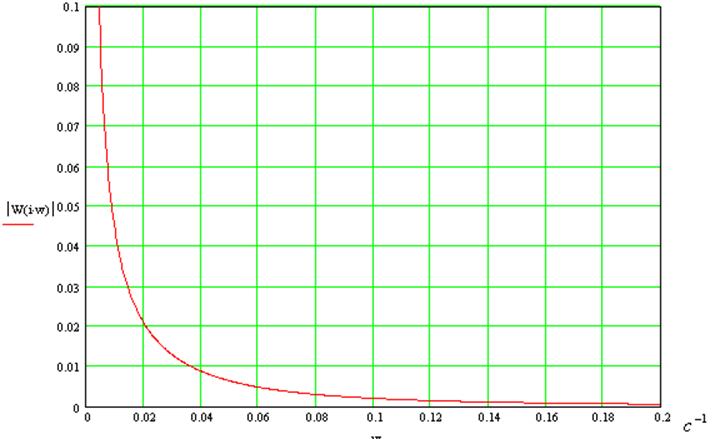
6. Амплитудно-частотная характеристика системы:
Передаточная функция системы в частотной области может быть получена заменой 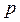
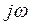
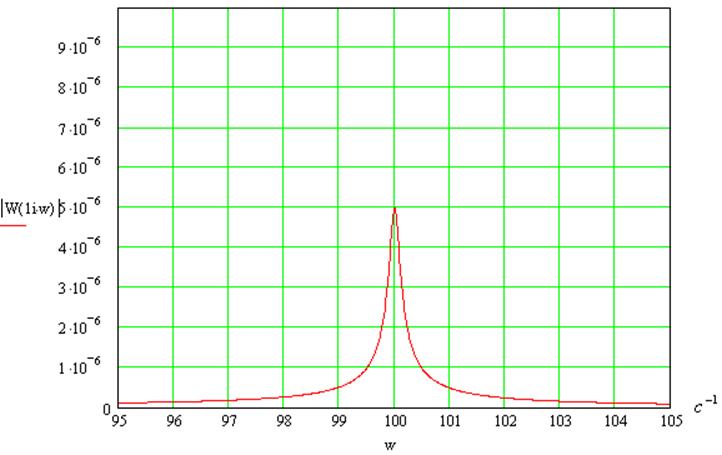
В области резонанса:
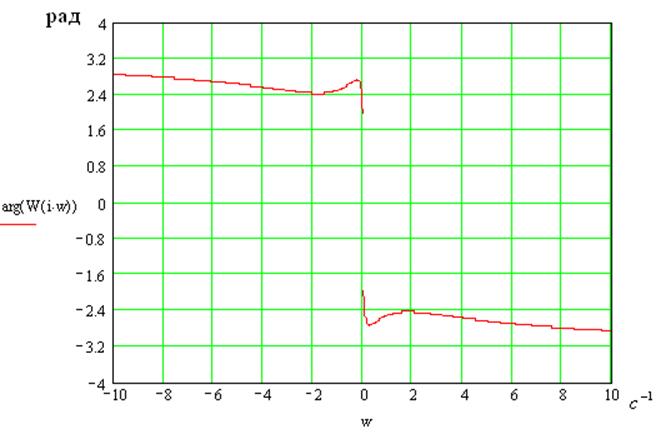
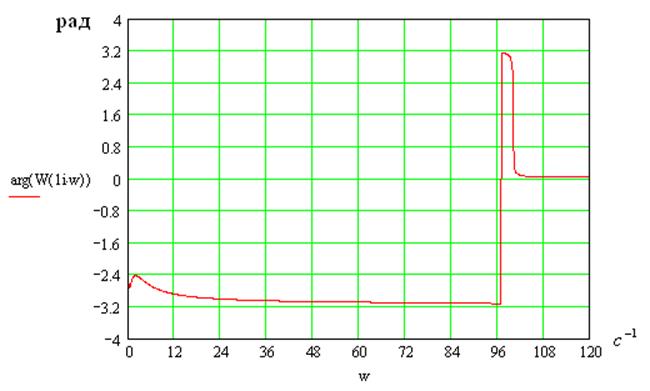
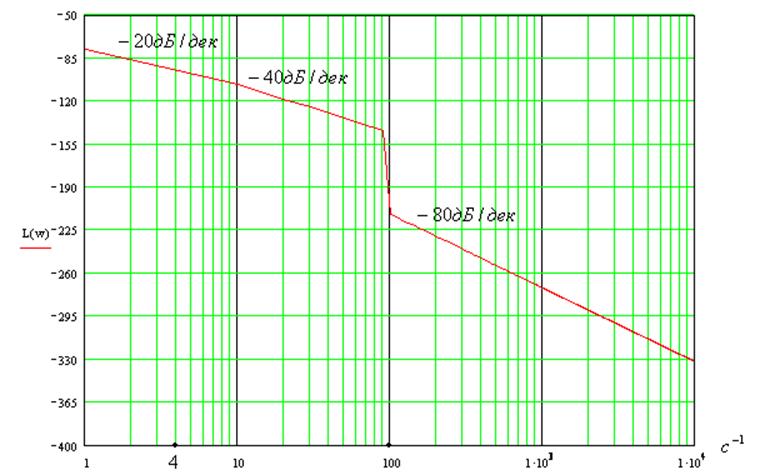
7. Фазо-частотная характеристика системы
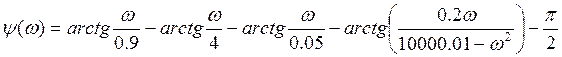
В области резонанса:
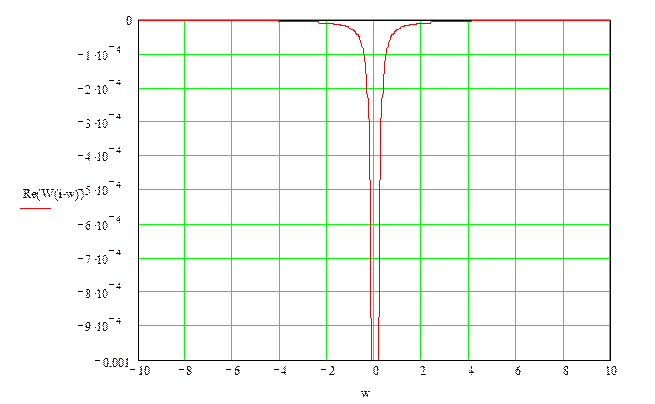
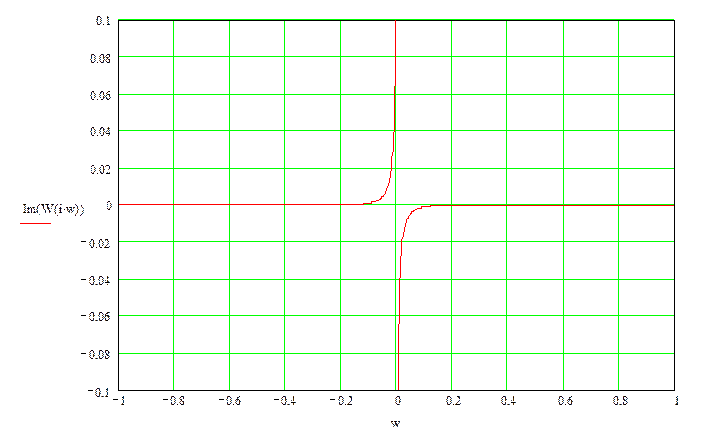
8. Амплитудно-фазовая характеристика системы:
Найдем реальную и мнимую части передаточной функции. Домножим числитель и знаменатель на комплексно сопряженное выражение
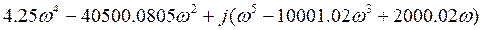
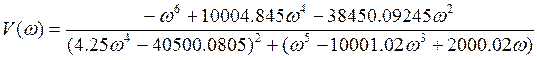
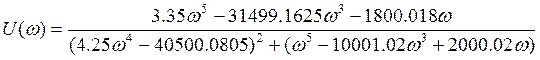
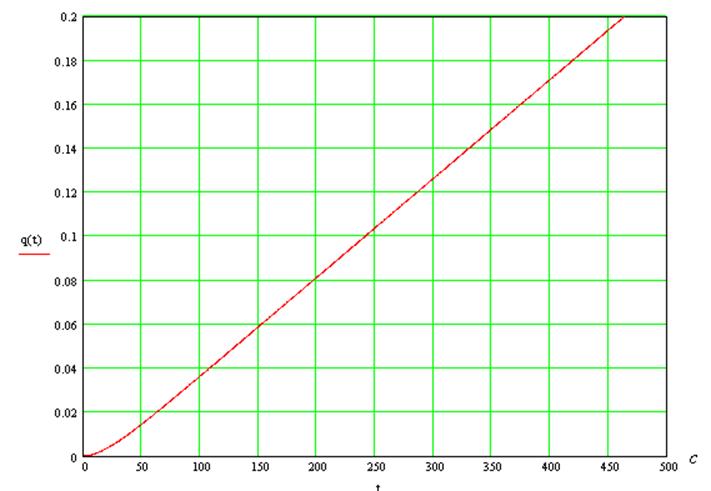
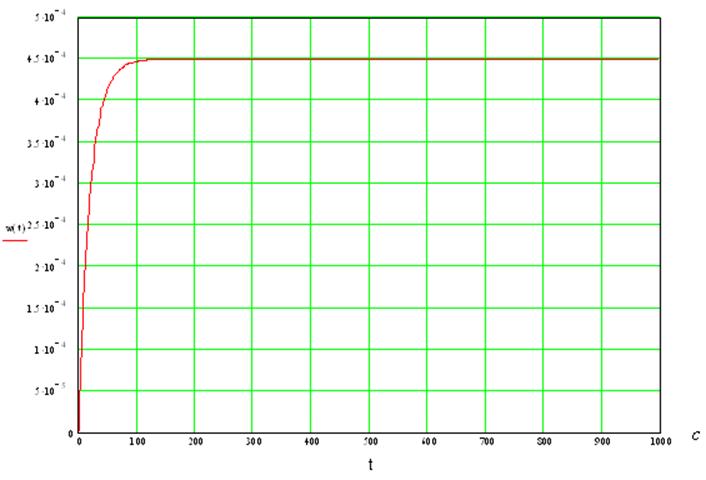
9. Определим переходную характеристику системы:
Переходная характеристика может быть выражена через передаточную функцию системы следующим образом:
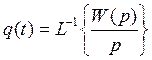
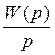
10. Определим весовую функцию, которая может быть выражена через передаточную функцию следующим образом:
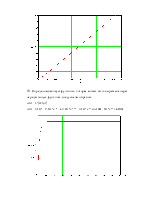
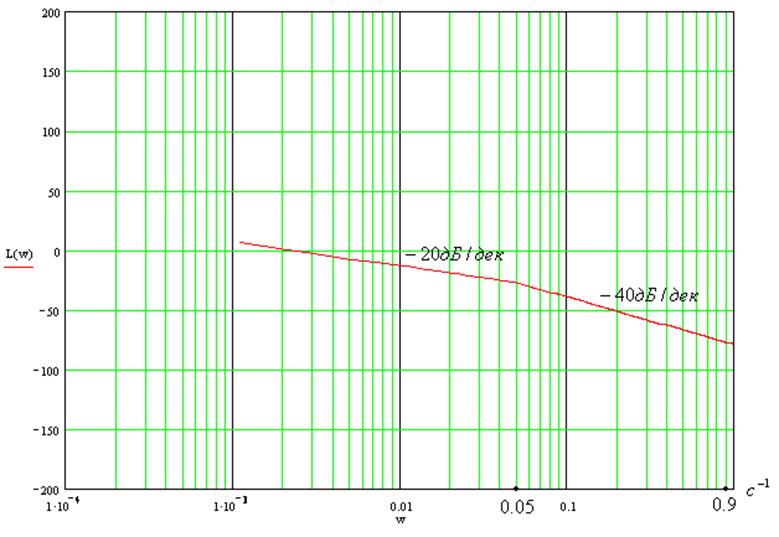
11. Найти и построить асимптотическую ЛАЧХ и ЛФЧХ:
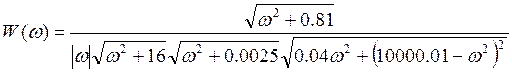
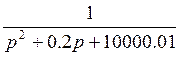
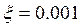
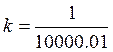
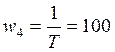
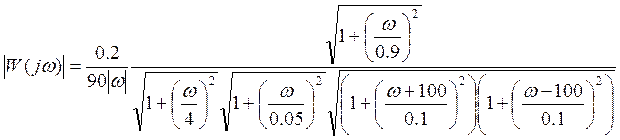
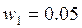
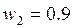
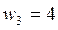
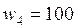
Тогда асимптотическую ЛАЧХ можно разбить на следующие интервалы:
При 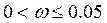
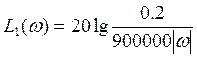
При 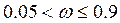
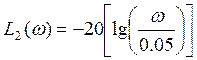
При 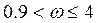
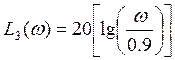
При:
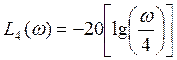
При 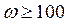
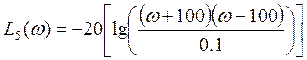
График асимптотической ЛАЧХ:
Для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения а0, т. е. при а0> 0 были положительными.
Рассчитаем определители, если характеристическое уравнение системы
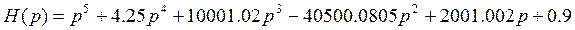
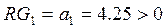
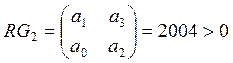
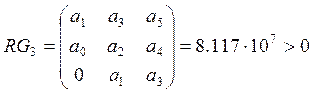
Так как все определители положительны, система устойчива.
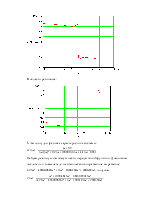
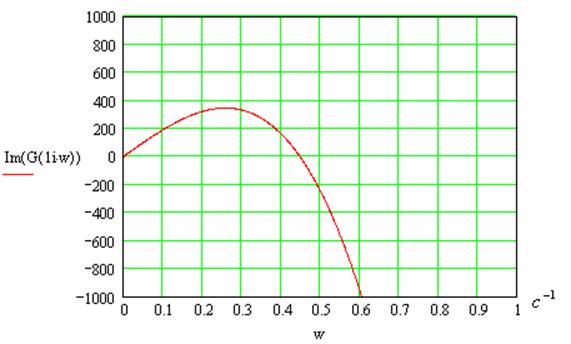
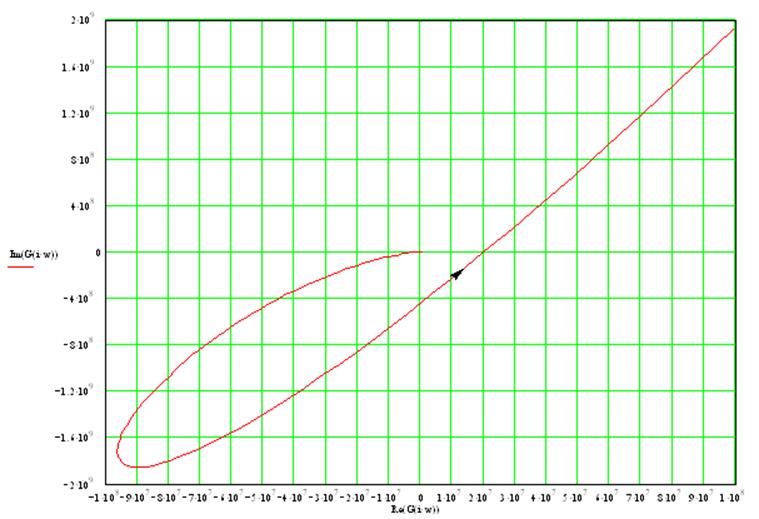
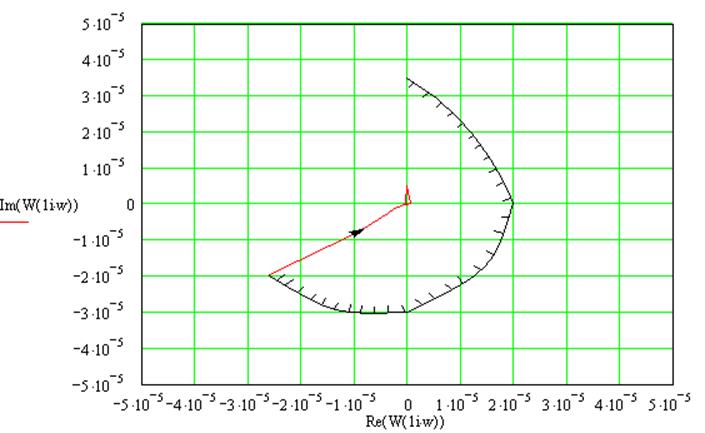
13. Проанализируем устойчивость системы методом Михайлова:
Для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы кривая (годограф) Михайлова при изменении частоты 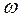
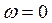
Вектор совершает поворот на 5 квадрантов, следовательно, система устойчива.
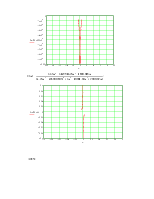
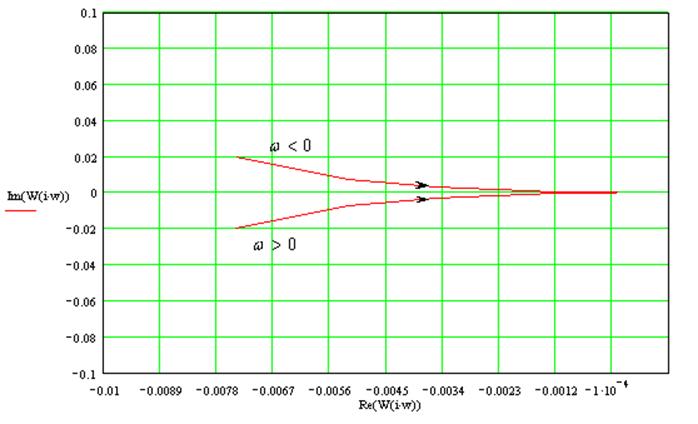
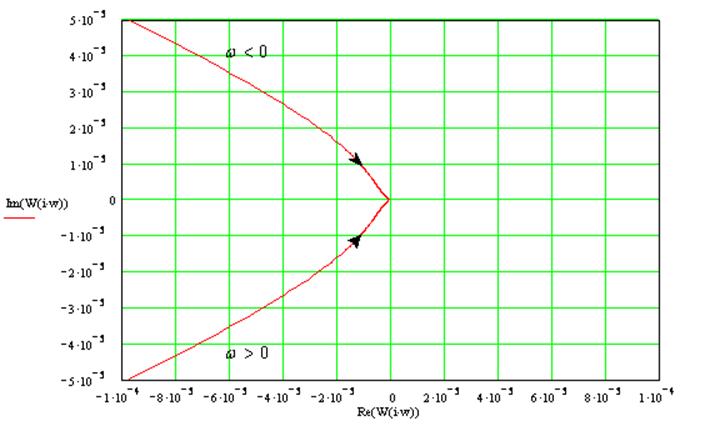
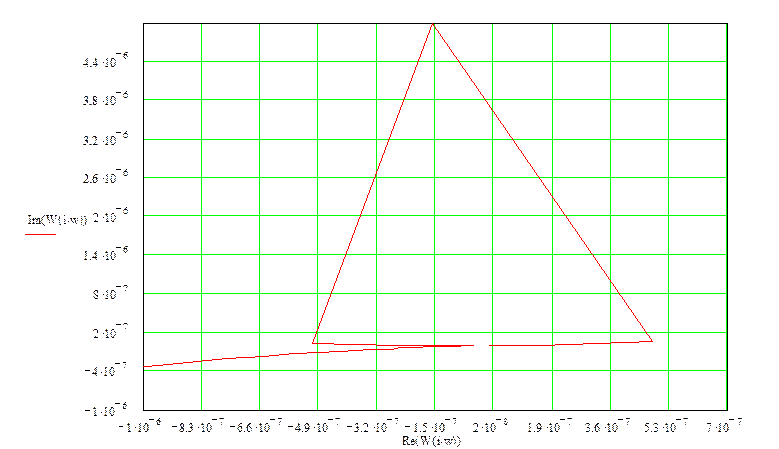
14. Проанализируем устойчивость системы методом Найквиста:
Для устойчивости астатической системы 1-го порядка необходимо и достаточно, чтобы годограф разомкнутой системы не охватывал точку -1+j0.
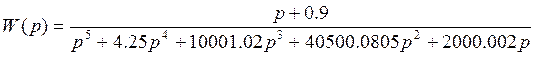
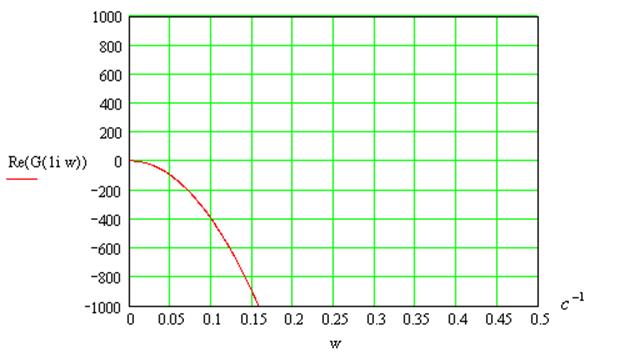
Годограф разомкнутой системы:
Годограф не охватывает точку -1+j0, следовательно, замкнутая система будет устойчива.
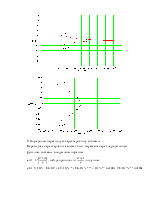
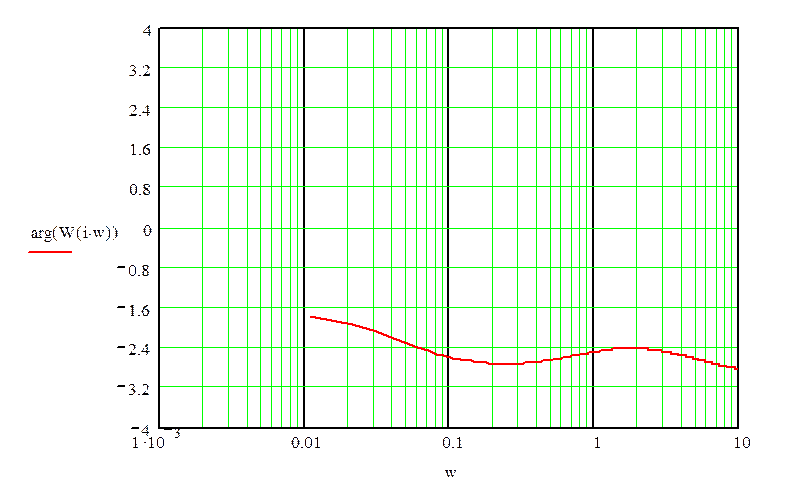
15. Анализ устойчивости по ЛАЧХ и ЛФЧХ:
Для устойчивости системы необходимо, чтобы число переходов ЛФЧХ через 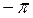
Видео:[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать
![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)
Передаточные функции систем автоматического управления
Записанные выше дифференциальные уравнения системы автоматического управления (5.4) и (5.6) могут быть получены также на основании понятия передаточной функции, которое было введено в главе 3. Рассмотрим рис. 5.1, где изображена замкнутая система автоматического управления.
Предположим вначале, что чувствительный элемент (ЧЭ) отсоединен от управляемого объекта (УО), и рассмотрим так называемую разомкнутую систему автоматического управления.
Управляющее воздействие, которое прикладывается к управляемому объекту, определяется выражением

Управляемая величина может быть найдена из выражения

передаточная функция объекта по
Первая из них определяется из дифференциального уравнения объекта (5.1) при
Передаточную функцию разомкнутой системы можно определить как отношение изображений управляемой величины и ошибки при нулевых начальных значениях и возмущающих воздействиях, равных нулю:



Учитывая (5.13), формулу (5.15) можно также записать в виде
Передаточная функция разомкнутой системы имеет весьма большое значение в теории автоматического управления, так как многие методы анализа и синтеза основаны на использовании именно этой функции.
Решая (5.12) и (5.17) совместно, получаем для управляемой величины
называется передаточной функцией замкнутой системы. Она устанавливает связь между управляемой величиной и задающим воздействием при равенстве пулю возмущающих воздействий:
называют передаточной функцией замкнутой системы по ошибке. Оно дает связь
между ошибкой и задающим воздействием в замкнутой системе при равенстве нулю возмущающих воздействий:

также при пулевых начальных условиях и отсутствии внешних возмущений.

когда цепь управления разорвана и автоматическое управление отсутствует.


Он равен сумме полиномов числителя и знаменателя передаточной функции разомкнутой системы (5.13).
Приравнивание нулю характеристического полинома (5.24) дает характеристическое уравнение замкнутой системы;
Оно может быть записано в более удобной форме, которая непосредственно получается из (5.18) или (5.19):
Полином знаменателя передаточной функции разомкнутой системы С(р) представляет собой характеристический полином разомкнутой системы.
Из рассмотренного видно, что знание передаточной функции разомкнутой системы позволяет найти выражение для ошибки и управляемой величины в функции задающего и возмущающих воздействий, а также характеристическое уравнение системы.
Передаточная функция разомкнутой системы может находиться непосредственно по структурной схеме и передаточным функциям входящих в нее звеньев.
🎥 Видео
23) Построение Л.А.Ч.Х. и Л.Ф.Ч.Х. системы по её передаточной функцииСкачать

Преобразование структурных схем систем управленияСкачать

proТАУ: 1. Передаточная функцияСкачать

1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия...Скачать

Теория автоматического управления. Лекция 6. Структурные схемы САУСкачать
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Дифференциальные уравнения. 11 класс.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Построить структурную схему САР (САУ) по передаточной функцииСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Передаточные функцииСкачать

Метод пространства состояний САУ: описание конкретной системыСкачать

✓Дифференцируемая функция. Дифференциал | матан #032 | Борис ТрушинСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать