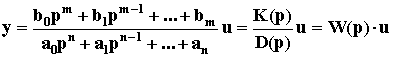Передаточная функция и дифференциальное уравнение в операторной форме

В ТАУ большое внимание уделяется исследованию САУ с одним входом и одним выходом, оператор которой — линейное дифференциальное уравнение с постоянными коэффициентами:

В левой части этого уравнения обычно пишут оператор выходного сигнала, в правой — оператор входного сигнала. Иссле дование дифференциальных уравнений существенно упрощается, если их преобразовать с помощью преобразования Лапласа.

Рассмотрим и этот вопрос для системы третьего порядка: a₃y (3> (t) + a₂y (t) + a₁y (t) + a_oy(t) = b₂x f2> ( t ) + b₁x ‘ V t ) + b_ox( t).

Напомним, что преобразование Лапласа при нулевых начальных условиях определяется формулами (2.2)

Применив преобразование Лапласа (2.2), к правой и левой части уравнения (2.7) при нулевых начальных условиях получим его операторную форму записи:

Операторная форма позволяет свести анализ дифференциальных уравнений к исследованию алгебраических уравнений. В общем виде операторное уравнение имеет вид:

Передаточная функция, характеристическое уравнение САУ

Передаточной функцией линейной стационарной САУ называется отношение изображения по Лапласу выходного сигнала Y(p) к такому же изображению входного сигнала Х(р) при нулевых начальных условиях:

Передаточная функция (ПФ) отражает передающие свойства САУ, поэтому при сс определении с целью упрощения исследований предполагается, что до начала воздействия входного сигнала САУ находится в покое.

Для определения W(p) необходимо записать оператор линейной стационарной САУ в операторной форме (2.8):

Тогда в соответствии с видом этого оператора

Таким образом, ПФ является дробно-рациональной функцией комплексной переменной преобразования Лапласа р, она не зависит от входного сигнала, а определяется структурой и параметрами САУ.

Знаменатель передаточной функции А(р) называется характеристическим полиномом, а уравнение

А( р) = а_пр п +. + aip + a₀ =0, называется характеристическим уравнением САУ.

Корни характеристического уравнения р. где i=0,n, называются полюсами передаточной функции. Они могут быть или действительными, или комплексно-сопряженными. Для наглядности их принято изображать на комплексной плоскости. Распределение полюсов на комплексной плоскости характеризуют основные свойства САУ.

Корни числителя передаточной функции

называются се н у л я м и .

САУ, все нули и полюса которой расположены в левой полуплоскости (имеют отрицательные действительные части), называются м и н и м а л ьн о — ф а з о в ы м и .

Определение и исследование передаточной функции и характеристического уравнения САУ занимают центральное место в ТАУ.

Преобразования Лапласа и Фурье

Напомним, что для сигналах(Г) (x(t) = 0 при t ±xp X(p)6, где (+т) — время упреждения, а (—т) — время запаздывания сигнала;

Изображения непрерывных и дискретных сигналов по Лапласу приведены в табл. П. 6.1.

Оригиналы и изображения непрерывных и дискретных сигналов по Лапласу

Переход от дифференциального уравнения к передаточной функции. Операторный метод нахождения реакции

Перейдем теперь от дифференциального уравнения (П6.1.1) как от уравнения для оригиналов (функций действительного аргумента t — в данном случае времени) к уравнению для изображений по Лапласу. Воспользовавшись свойством линейности, соотношениями (П6.2.2) и аналогичными соотношениями для реакции системы после почленного перехода от оригиналов к изображениям при нулевых начальных условиях, получим уравнение для изображений

Данные уравнения по внешнему виду напоминают уравнения (П6.1.3) и (П6.1.4) для оригиналов. Однако переменная р в них имеет различный смысл. Уравнения (П6.3.1), (П6.3.2) можно переписать в виде

Это отношение изображения выхода Y(p) к изображению входа Х(р) по Лапласу при нулевых начальных условиях называется передаточной функцией системы.

Из (П6.3.3) следует, что

т.е. в области изображений определение реакции сводится к алгебраической операции умножения, что упрощает нахождение реакции.

Операторный метод решения (с помощью преобразования Лапласа) сводится к трем действиям:

• 1. От оригинала x(t) по формуле (П6.2.1) переходят к изображению X (р).
• 2. По формуле (П6.3.4) находят изображение реакции.
• 3. По формуле обратного преобразования Лапласа находят реакцию.

Частным случаем передаточной функции является частотная передаточная функция, равная отношению изображений по Фурье выхода ко входу, т.е.

Изображение по Фурье является частным случаем преобразования Лапласа при р = усо, например

Используя преобразование Фурье, можно аналогично найти реакцию y(t) на сигнал y(t).

На практике переход от оригиналов к изображениям и обратно осуществляется с помощью таблицы преобразования Лапласа. Если изображение реакции сложное, то для перехода к оригиналу (самой реакции) изображение разлагают на сумму простых дробей и делают переход для каждой дроби на основании линейности преобразования Лапласа.

Передаточная функция. В ТАУ часто используют операторную форму записи дифференциальных уравнений

В ТАУ часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператораp = d/dt так, что, dy/dt = py, а p n = d n /dt n . Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p. В операторной форме исходное дифференциальное уравнение записывается как алгебраическое:

Не надо путать эту форму записи с операционным исчислением хотя бы потому, что здесь используются непосредственно функции времени y(t), u(t) (оригиналы), а не их изображения Y(p), U(p), получаемые из оригиналов по формуле преобразования Лапласа. Вместе с тем при нулевых начальных условиях с точностью до обозначений записи действительно очень похожи. Это сходство лежит в природе дифференциальных уравнений. Поэтому некоторые правила операционного исчисления применимы к операторной форме записи уравнения динамики. Так оператор p можно рассматривать в качестве сомножителя без права перестановки, то есть py 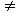yp. Его можно выносить за скобки и т.п.

Поэтому уравнение динамики можно записать также в виде:

Дифференциальный оператор W(p) называют передаточной функцией. Она определяет отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/u(t), поэтому ее еще называют динамическим коэффициентом усиления. В установившемся режиме d/dt = 0, то есть p = 0, поэтому передаточная функция превращается в коэффициент передачи звена K = b_m/a_n.

Знаменатель передаточной функции D(p) = a_op n + a₁p n — 1 + a₂p n — 2 + . + a_n называют характеристическим полиномом. Его корни, то есть значения p, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функции.

Числитель K(p) = b_op m + b₁p m — 1 + . + b_m называют операторным коэффициентом передачи. Его корни, при которых K(p) = 0 и W(p) = 0, называются нулями передаточной функции.

Звено САУ с известной передаточной функцией называется динамическим звеном. Оно изображается прямоугольником, внутри которого записывается выражение передаточной функции. То есть это обычное функциональное звено, функция которого задана математической зависимостью выходной величины от входной в динамическом режиме. Для звена с двумя входами и одним выходом должны быть записаны две передаточные функции по каждому из входов. Передаточная функция является основной характеристикой звена в динамическом режиме, из которой можно получить все остальные характеристики. Она определяется только параметрами системы и не зависит от входных и выходных величин. Например, одним из динамических звеньев является интегратор. Его передаточная функция W_и(p) = 1/p. Схема САУ, составленная из динамических звеньев, называется структурной.

Дата добавления: 2015-12-26 ; просмотров: 868 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

🎥 Видео