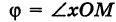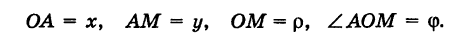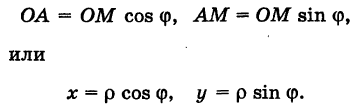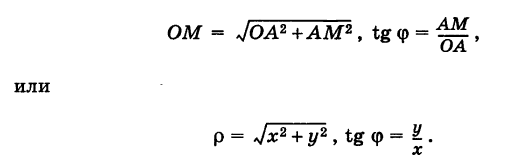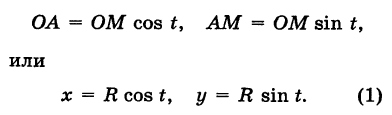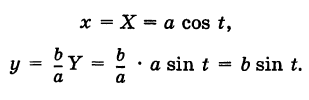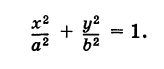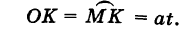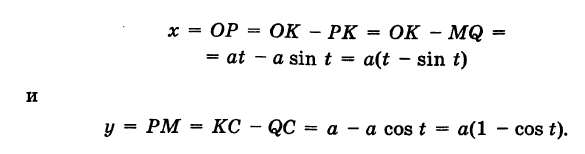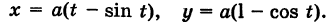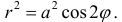Содержание:
- Полярные координаты. параметрические уравнения линии
- Полярные координаты
- Связь между прямоугольными и полярными координатами
- Параметрические уравнения линии
- Параметрические уравнения циклоиды
- Полярная система координат
- Параметрические уравнения прямой на плоскости: описание, примеры, решение задач
- Вывод параметрических уравнений прямой на плоскости
- Составление параметрических уравнений прямой на плоскости
- Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно
- Примеры и задачи с параметрическими уравнениями прямой на плоскости
- Параметрическое уравнение прямой на плоскости
- Приведение параметрического уравнения на плоскости к каноническому виду
- Приведение параметрического уравнения на плоскости к общему виду
- 💥 Видео
Видео:Параметрические уравнения прямойСкачать

Полярные координаты. параметрические уравнения линии
Полярные координаты
Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.
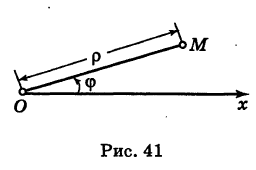
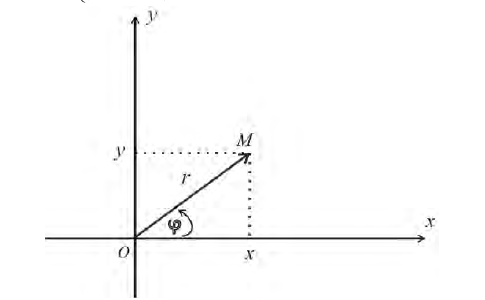
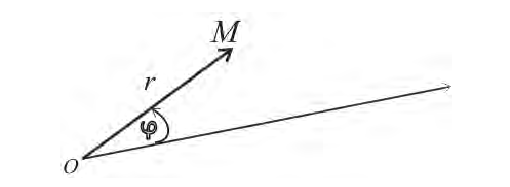
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол
Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до 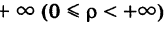
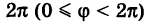
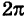
Связь между прямоугольными и полярными координатами
Рассмотрим переход от полярных координат к прямоугольным и обратно.
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).
Тогда для произвольной точки М имеем
Считая угол ф острым, из прямоугольного треугольника АОМ находим
Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем
Так выражаются полярные координаты точки через ее прямоугольные координаты.
Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.
Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.
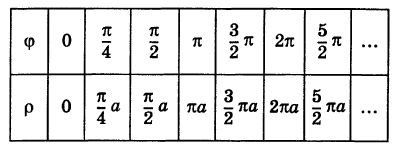
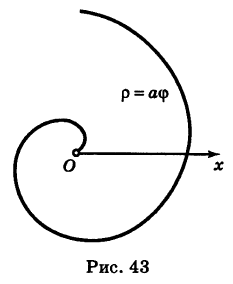
Пример:
Рассмотрим кривую 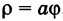
По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).
Параметрические уравнения линии
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 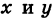
Пример:
Выведем параметрические уравнения окружности.
Пусть М 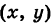
Это и есть параметрические уравнения окружности.
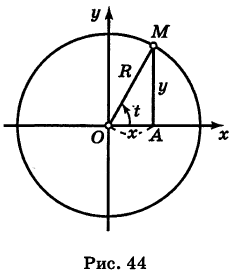
Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:
Пример:
Выведем параметрические уравнения эллипса.
Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где
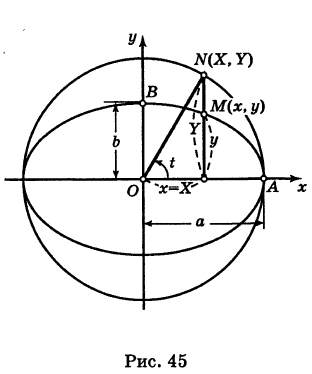
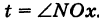
Таким образом, параметрические уравнения эллипса с полуосями а и b есть
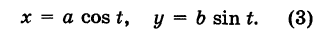
Имея параметрические уравнения линии, можно по точкам построить ее.
Пример:
Решение:
Составляем таблицу значений:
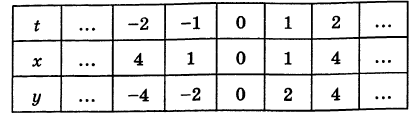
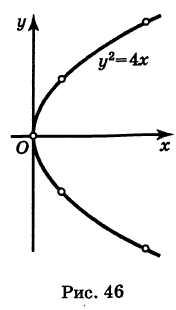
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 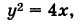
Параметрические уравнения циклоиды
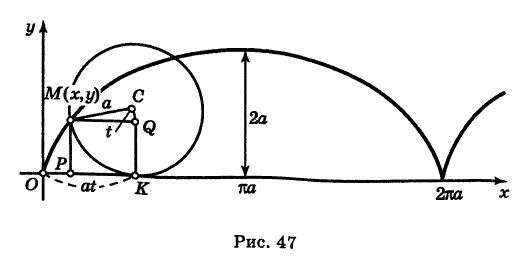
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).
Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем
Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:
Таким образом, параметрические уравнения циклоиды есть
Полярная система координат
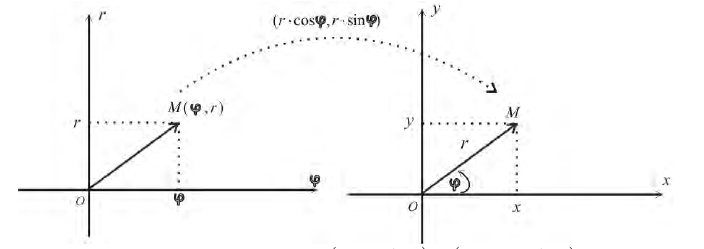
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 
Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:
Пример 1.
Построим на плоскости линию, заданную уравнением:
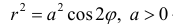
Решение.
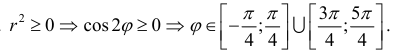
Вычислим значения r при различных значениях ϕ : 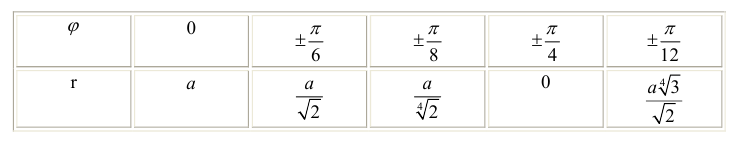
Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :
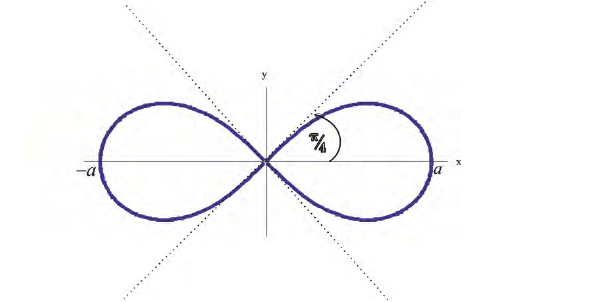
Рис.3. Лемниската
Пример 2.
а) Построим кривую 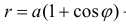
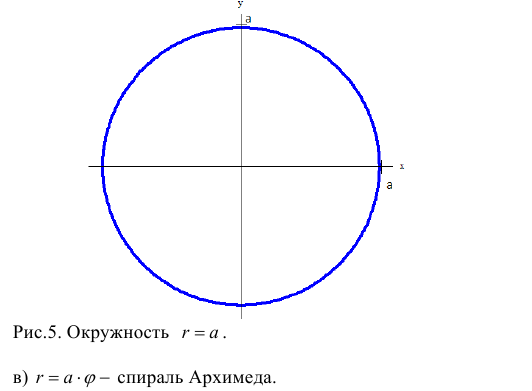
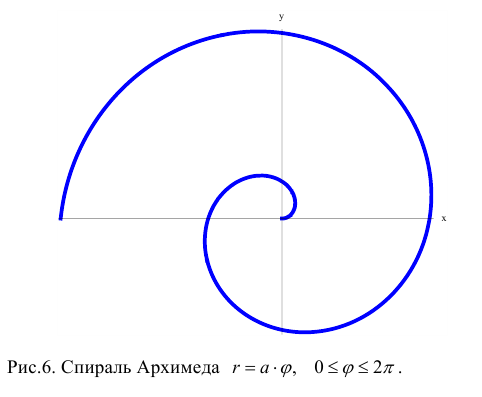
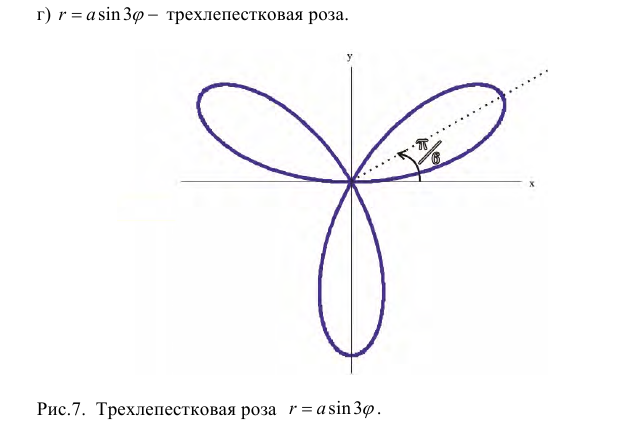
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).
При этом, если r > 0, то векторы 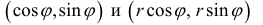
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Параметрические уравнения прямой на плоскости: описание, примеры, решение задач
Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.
Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Вывод параметрических уравнений прямой на плоскости
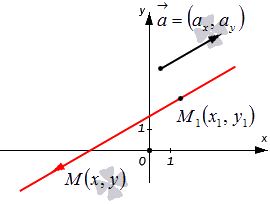
Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.
Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.
Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x — x 1 , y — y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) являются коллинеарными.
Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:
M 1 M → = λ · a → , где λ – некоторое действительное число.
Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.
В координатной форме оно имеет вид:
M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ
Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Составление параметрических уравнений прямой на плоскости
Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.
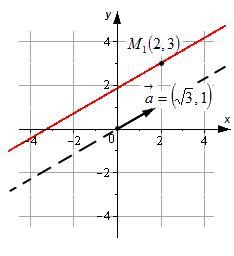
Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .
Решение
На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ
Ответ: x = 2 + 3 · λ y = 3 + λ
Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .
К примеру, нам заданы направляющий вектор прямой a → = ( 2 , — 1 ) , а также точки М 1 ( 1 , — 2 ) и М 2 ( 3 , — 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = — 2 — λ или x = 3 + 2 · λ y = — 3 — λ .
Следует обратить внимание и на такой факт: если a → = ( a x , a y ) — направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .
Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.
Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = — 2 — 5 · λ . Тогда a → = ( 2 , — 5 ) — направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · — 5 ) = 2 μ , — 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор — 2 · a → = ( — 4 , 10 ) , ему соответствует значение μ = — 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 — 4 · λ y = — 2 + 10 · λ .
Видео:1 серия "Параметрическое уравнение прямой" из курса видеолекций "Метод координат"Скачать

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно
В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.
Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x — x 1 a x = y — y 1 a y .
Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y
При этом не должно смущать, если a x или a y будут равны нулю.
Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = — 2 — 4 · λ к каноническому уравнению.
Решение
Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = — 2 — 4 · λ
Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4
Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:
x — 3 0 = y + 2 — 4
Ответ: x — 3 0 = y + 2 — 4
В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y ⇔ ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ A x + B y + C = 0
Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = — 1 + 2 · λ y = — 3 · λ
Решение
Для начала осуществим переход к каноническому уравнению:
x = — 1 + 2 · λ y = — 3 · λ ⇔ λ = x + 1 2 λ = y — 3 ⇔ x + 1 2 = y — 3
Полученная пропорция идентична равенству — 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: — 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .
Ответ: 3 x + 2 y + 3 = 0
Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.
Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.
Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x — x 1 a x = y — y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :
x — x 1 a x = y — y 1 a y = λ ⇔ λ = x — x 1 a x λ = y — y 1 a y
Разрешим полученные уравнения относительно переменных x и y :
x = x 1 + a x · λ y = y 1 + a y · λ
Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x — 2 5 = y — 2 2
Решение
Приравняем части известного уравнения к параметру λ : x — 2 5 = y — 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x — 2 5 = y — 2 2 = λ ⇔ λ = x — 2 5 λ = y — 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ
Ответ: x = 2 + 5 · λ y = 2 + 2 · λ
Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.
Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x — 3 y — 3 = 0 .
Решение
Заданное общее уравнение преобразуем в уравнение канонического вида:
4 x — 3 y — 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4
Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:
x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = — 1 3 + 4 · λ
Ответ: x = 3 · λ y = — 1 3 + 4 · λ
Видео:Прямоугольная система координат в пространстве. 11 класс.Скачать

Примеры и задачи с параметрическими уравнениями прямой на плоскости
Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.
- В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.
Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.
Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 — 1 6 · λ y = — 1 + 2 · λ при λ = 3 .
Решение
Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 — 1 6 · 3 y = — 1 + 2 · 3 ⇔ x = 1 1 2 y = 5
Ответ: 1 1 2 , 5
Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .
Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.
Заданы точки М 0 ( 4 , — 2 ) и N 0 ( — 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = — 1 — 1 2 · λ .
Решение
Подставим координаты точки М 0 ( 4 , — 2 ) в заданные параметрические уравнения:
4 = 2 · λ — 2 = — 1 — 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2
Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .
Далее по аналогии проверим заданную точку N 0 ( — 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:
— 2 = 2 · λ 1 = — 1 — 1 2 · λ ⇔ λ = — 1 λ = — 4
Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( — 2 , 1 ) .
Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.
- В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.
Пример 8
Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y — 3 — 1 .
Решение
По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y — 3 — 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y — 3 — 1 , который запишем в виде: a → = ( 2 , — 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( — 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 — λ
Ответ: x = 1 2 + x · λ y = 2 3 — λ .
Задана точка М 1 ( 0 , — 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .
Решение
В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , — 2 ) . Запишем требуемые параметрические уравнения прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = — 7 + ( — 2 ) · λ ⇔ x = 3 · λ y = — 7 — 2 · λ
Ответ: x = 3 · λ y = — 7 — 2 · λ
- В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.
Пример 10
Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 — 3 4 · λ y = — 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.
Решение
Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:
x = 1 — 3 4 · λ y = — 1 + λ ⇔ λ = x — 1 — 3 4 λ = y + 1 1 ⇔ x — 1 — 3 4 = y + 1 1 ⇔ ⇔ 1 · x — 1 = — 3 4 · y + 1 ⇔ x + 3 4 y — 1 4 = 0
Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 — 3 4 · λ y = — 1 + λ имеет координаты 1 , 3 4 .
Видео:11. Прямая в пространстве и ее уравненияСкачать

Параметрическое уравнение прямой на плоскости
В данной статье мы рассмотрим параметрическое уравнение прямой на плоскости. Приведем примеры построения параметрического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим методы преобразования уравнения в параметрическом виде в канонический и общий виды.
Параметрическое уравнение прямой L на плоскости представляется следующей формулой:
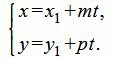 | (1) |
Отметим что при записи уравнения прямой в параметрическом виде, направляющий вектор прямой не должен быть нулевым вектором, т.е хотя бы один координат направляющего вектора q должен быть отличным от нуля.
Для построения прямой на плоскости в декартовой прямоугольной системе координат, заданной параметрическим уравнением (1), достаточно задать параметру t две разные значения, вычислить x и y и провести через эти точки прямую линию. При t=0 имеем точку M1(x1, y1) при t=1, получим точку M2(x1+m, y1+p).
Для составления параметрического уравнения прямой на плоскости L достаточно иметь точку на прямой L и направляющий вектор прямой или две точки, принадлежащие прямой L. В первом случае, для построения параметрического уравнения прямой нужно координаты точки и направляющего вектора вставить в уравнение (1). Во втором случае сначала нужно найти направляющий вектор прямой q=<m, p>, вычисляя разности соответствующих координатов точек M1 и M2: m=x2−x1, p=y2−y1(Рис.1). Далее, аналогично первому случаю, подставить координаты одной из точек (не имеет значение какой именно) и направляющего вектора q прямой в (1).
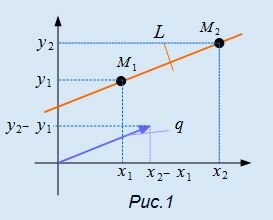 |
Можно также вывести формулу параметрического уравнения прямой, проходящей через две точки. Для этого подставим значения m=x2−x1, p=y2−y1 в (1), получим параметрическое уравнение прямой на плоскости, проходящей через точки M1(x1, y1) и M2(x2, y2):
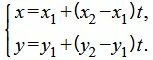 | (2) |
Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=. Построить параметрическое уравнение прямой.
Решение. Для построения параметрического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):
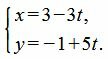 |
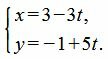 |
Пример 2. Прямая проходит через точки M1=(−5, 2) и M2=(−2, 3). Построить параметрическое уравнение прямой.
Решение. Воспользуемся формулой (2). Подставим координаты точек M1 и M2 в уравнение (2):
 |
Упростим полученное уравнение:
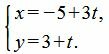 |
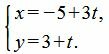 |
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Приведение параметрического уравнения на плоскости к каноническому виду
Выразим параметр t в (1) через переменные x и y:
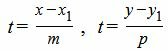 | (3) |
Из выражений (3), можем записать каноническое уравнение прямой на плоскости:
 . . | (4) |
Обратное преобразование смотрите здесь.
Пример 3. Прямая на плоскости представлена следующим параметрческим уравнением:
 |
Привести данное уравнение прямой к каноническому виду.
Решение: Выразим параметр t через переменные x и y:
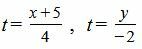 | (5) |
Из выражений (5), можем записать:
 |
 |
Видео:Полярная система координатСкачать

Приведение параметрического уравнения на плоскости к общему виду
Для приведения параметрического уравнения прямой на плоскости к общему виду, в формулах (1) выразим из второго уравнения параметр t через переменную y и подставим в первое уравнение:
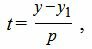 |
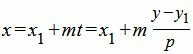 | (6) |
Умножим обе части уравнения (6) на p и группируем элементы уравнения:
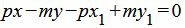 . . | (7) |
Сделаем обозначения: A=p, B=−m, C=−px1+my1. Тогда получим общее уравнение прямой:
Обратное преобразование смотрите здесь.
Пример 4. Прямая на плоскости представлена следующим параметрческим уравнением:
 | (9) |
Привести данное уравнение прямой к общему виду.
Решение: В уравнении (9) имеем: x1=−5, y1=0, m=4, p=−2. Подставим эти значения в формулу (7):
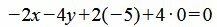 | (10) |
Упростив выражение (10) получим общее уравнение прямой (9):
💥 Видео
11 класс, 1 урок, Прямоугольная система координат в пространствеСкачать

Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Построение кривой в полярной системе координатСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Прямоугольная система координат в пространстве. Координаты вектора. Видеоурок по геометрии 11 классСкачать

Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

9 класс, 7 урок, Уравнение прямойСкачать

§49 Параметрические уравнения прямойСкачать

Прямоугольная система координат. Координатная плоскость. 6 класс.Скачать