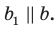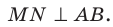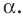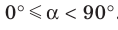В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.
- Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой
- Решение примеров
- Уравнение перпендикуляра к прямой в пространстве
- Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой
- Решение примеров
- Перпендикулярность в пространстве с примерами решения
- Перпендикулярность в пространстве
- Угол между прямыми в пространстве
- Перпендикулярность прямой и плоскости
- Перпендикуляр и наклонная
- Угол между прямой и плоскостью
- Двугранный угол. Угол между плоскостями
- 📺 Видео
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой
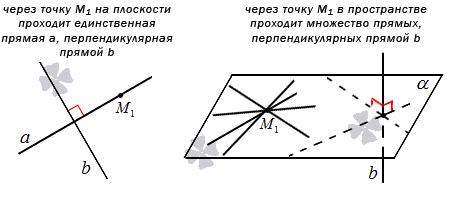
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.
Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .
Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.
Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .
По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .
Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = — 1 .
Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор — n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x — x 1 ) + B 2 · ( y — y 1 ) = 0 .
Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x — x 1 a x = y — y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.
После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен — 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом — 1 k b в виде y — y 1 = — 1 k b · ( x — x 1 ) .
Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.
Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Решение примеров
Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.
Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , — 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x — 2 3 = y + 4 1 .
Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x — 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , — 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .
Получим уравнение вида: 3 · ( x — 7 ) + 1 · ( y — ( — 9 ) ) = 0 ⇔ 3 x + y — 12 = 0
Полученное уравнение является искомым.
Ответ: 3 x + y — 12 = 0 .
Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x — y + 1 = 0 .
Имеем, что n b → = ( 2 , — 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , — 1 ) — координаты искомого направляющего вектора прямой.
Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , — 1 ) . Получим, что x — 0 2 = y + 0 — 1 ⇔ x 2 = y — 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x — y + 1 = 0 .
Ответ: x 2 = y — 1 .
Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 .
Из уравнения y = — 5 2 x + 6 угловой коэффициент имеет значение — 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение — 1 — 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 , равна y — ( — 3 ) = 2 5 · x — 5 ⇔ y = 2 5 x — 5 .
Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Уравнение перпендикуляра к прямой в пространстве
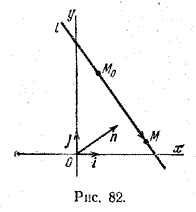
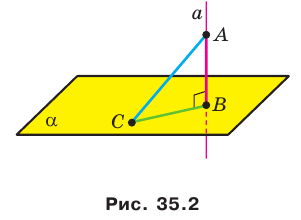
Пусть дана некоторая точка М и вектор n. Проведем через точку М прямую l перпендикулярно вектору n (рис. 82).
Пусть M – произвольная точка. Точка M лежит на прямой l в том и только в том случае, когда вектор (overrightarrow M>) перпендикулярен вектору n, а для этого необходимо и достаточно, чтобы скалярное произведение векторов n и (overrightarrow M>) равнялось нулю:
Чтобы выразить последнее равенство в координатах, введем прямоугольную декартову систему координат. Пусть точки M и M имеют координаты (x ; у ) и (x; у).
Тогда (overrightarrow M>) = (x – x ; у – у ). Обозначим координаты нормального вектора n через (А; В). Теперь равенство (1) можно записать так:
Уравнение (2) есть уравнение прямой l, проходящей через данную точку М (x ; у ) перпендикулярно данному вектору n = (А; В).
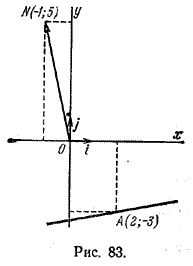
Задача 1. Составить уравнение прямой, проходящей через точку А (2; -3) перпендикулярно вектору n = (-1;5) (рис.83).
Пользуясь формулой (2), находим уравнение данной прямой:
– 1 • (x-2) + 5 • (у + 3) = 0
или, окончательно, x – 5у – 17 = 0.
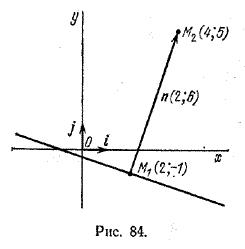
Задача 2. Даны точки M1(2; -1) и M2(4; 5). Написать уравнение прямой, проходящей через точку М1 перпендикулярно вектору (overrightarrow M_ >).
Нормальный вектор искомой прямой n = (overrightarrow M_ >) имеет координаты (2; 6) (рис. 84).
Следовательно, по формуле (2) получим уравнение
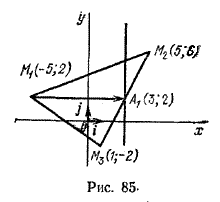
Задача 3. В треугольнике с вершинами в точках M1(-5; 2), M2(5; 6) и M3(1; -2) проведена медиана M1А1. Требуется составить уравнение прямой, проходящей через точку А1 перпендикулярно медиане M1A1 (рис. 85).
За нормальный вектор искомой прямой можно принять вектор n = (overrightarrow A_ >). Определим его координаты. Точка A1 – середина отрезка M2M3, поэтому, если (x1; y1) – ее координаты, то ( x_1 = frac =3, ;;а ;; y_1=frac =2 ).
Тогда нормальный вектор n = (overrightarrow A_ >) имеет координаты (8; 0). Следовательно, искомое уравнение прямой имеет вид
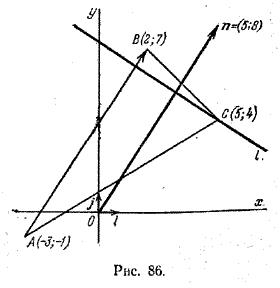
Задача 4. Дан треугольник с вершинами в точках А(-3; -1), В(2; 7) и С(5; 4). Требуется составить уравнение прямой, проходящей через вершину С перпендикулярно стороне AB (рис. 86).
За нормальный вектор искомой прямой можно взять вектор n = (overrightarrow).
Так как n = (2-(-3); 7 – (-1)) = (5; 8), то, подставляя координаты точки С и координаты вектора n в формулу (2), получим
или, окончательно, 5х + 8у – 57 = 0.
В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.
Видео:11. Прямая в пространстве и ее уравненияСкачать

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.
Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .
Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.
Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .
По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .
Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = – 1 .
Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор – n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x – x 1 ) + B 2 · ( y – y 1 ) = 0 .
Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x – x 1 a x = y – y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.
После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен – 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом – 1 k b в виде y – y 1 = – 1 k b · ( x – x 1 ) .
Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.
Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Решение примеров
Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.
Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , – 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x – 2 3 = y + 4 1 .
Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x – 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , – 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .
Получим уравнение вида: 3 · ( x – 7 ) + 1 · ( y – ( – 9 ) ) = 0 ⇔ 3 x + y – 12 = 0
Полученное уравнение является искомым.
Ответ: 3 x + y – 12 = 0 .
Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x – y + 1 = 0 .
Имеем, что n b → = ( 2 , – 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , – 1 ) – координаты искомого направляющего вектора прямой.
Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , – 1 ) . Получим, что x – 0 2 = y + 0 – 1 ⇔ x 2 = y – 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x – y + 1 = 0 .
Ответ: x 2 = y – 1 .
Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , – 3 ) перпендикулярно прямой y = – 5 2 x + 6 .
Из уравнения y = – 5 2 x + 6 угловой коэффициент имеет значение – 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение – 1 – 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , – 3 ) перпендикулярно прямой y = – 5 2 x + 6 , равна y – ( – 3 ) = 2 5 · x – 5 ⇔ y = 2 5 x – 5 .
Альтернативная формула
Прямая, проходящая через точку M1(x1; y1) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением
назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).
Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /9x – 1 /3 (a = 4 /9). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .
Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .
Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Перпендикулярность в пространстве с примерами решения
Содержание:
Видео:18. Расстояние от точки до прямой в пространствеСкачать

Перпендикулярность в пространстве
В этом параграфе вы ознакомитесь с понятиями угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями; узнаете, что такое ортогональная проекция, изучите свойство ортогональной проекции многоугольника.
Угол между прямыми в пространстве
Поскольку две любые пересекающиеся прямые пространства лежат в одной плоскости, то угол между ними определим так же, как в планиметрии. Определение. Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает 
Угол между двумя параллельными прямыми считают равным 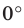
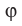
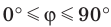
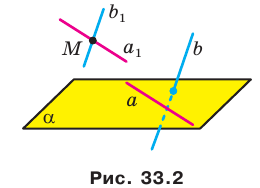
Введем понятие угла между скрещивающимися прямыми. Определение. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Пусть прямые 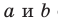
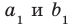
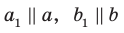
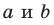
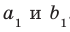
Возникает естественный вопрос: зависит ли угол между данными скрещивающимися прямыми 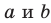
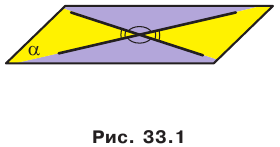
Теорема 33.1. Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, соответственно параллельными данным.
Воспользовавшись теоремой 33.1, можно показать, что угол между скрещивающимися прямыми 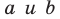
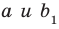
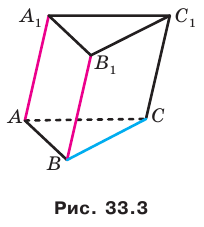
Например, на рисунке 33.3 изображена треугольная призма 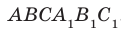
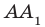
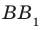
Определение. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Заметим, что перпендикулярные прямые могут как пересекаться, так и быть скрещивающимися.
Если прямые 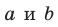
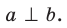
Например, ребра AD и 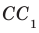
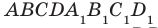
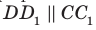
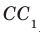
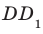
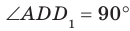
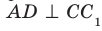
Пример:
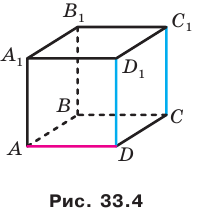
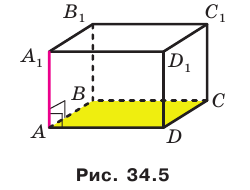
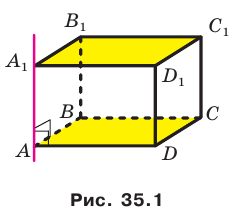
На рисунке 33.5 изображен куб 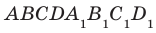
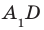
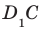
Решение:
Соединим точки 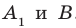
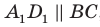
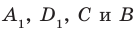
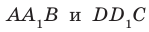
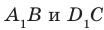
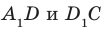
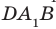
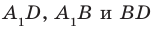
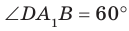
Перпендикулярность прямой и плоскости
В повседневной жизни мы говорим: флагшток перпендикулярен поверхности земли (рис. 34.1), мачты парусника перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивают в доску перпендикулярно ее поверхности (рис. 34.3) и т.п.

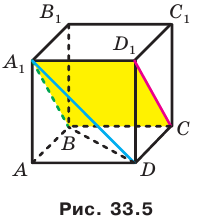
Эти примеры дают представление о прямой, перпендикулярной плоскости. Определение. Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости (рис. 34.4).
Если прямая 
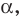
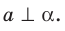
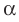
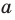
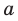
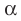
Из определения следует, что если прямая 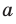
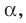
Отрезок называют перпендикулярным плоскости, если он принадлежит прямой, перпендикулярной этой плоскости.
Например, интуитивно понятно, что ребро 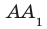
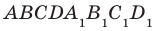
Теорема 34.1 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
На рисунке 34.5 прямая 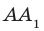
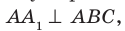
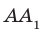
Теорему 34.1 часто используют на практике. Например, подставка для новогодней елки имеет форму крестовины. Если елку установить так, чтобы ее ствол был перпендикулярен направлениям крестовины, то елка будет стоять перпендикулярно плоскости пола (рис. 34.6).
Приведем теорему, которую можно рассматривать как еще один признак перпендикулярности прямой и плоскости.
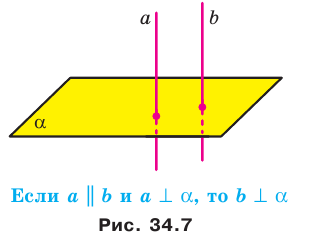
Теорем а 34.2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 34.7).
Например, на рисунке 34.5 прямая 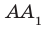
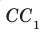
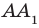
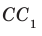
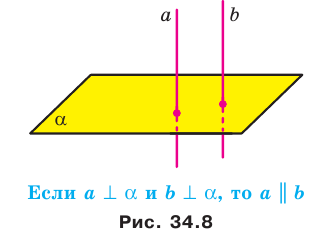
Теорем а 34.3. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны (рис. 34.8). Справедлива и такая теорема.
Теорема 34.4. Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
Пример:
Плоскость 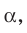
Решение:
Поскольку прямая АС перпендикулярна плоскости 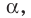

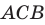
Перпендикуляр и наклонная
Пусть фигура 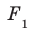
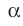
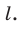
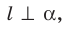
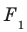
Например, основание ABCD прямоугольного параллелепипеда 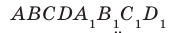
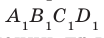
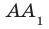
В дальнейшем, говоря о проекции фигуры, если не оговорено противное, будем иметь в виду ортогональную проекцию.
Пусть даны плоскость 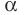
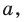
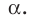
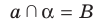
Отрезок АВ называют перпендикуляром, опущенным из точки А на плоскость 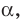
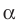
Отметим на плоскости 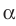
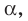
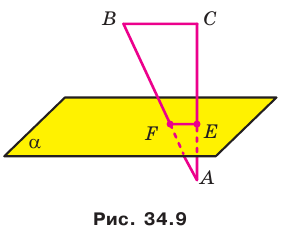
Теорема 35.1. Если из одной тонки проведены к плоскости перпендикуляр и наклонная, то наклонная больше перпендикуляра.
Пример:
Докажите, что если точка, не принадлежащая плоскости многоугольника, равноудалена от его вершин, то проекцией этой точки на плоскость многоугольника является центр его описанной окружности.
Решение:
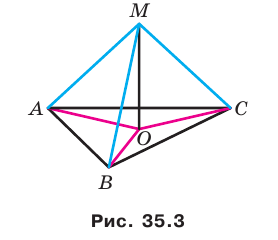
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Пусть точка М не принадлежит плоскости АВС, причем МА = = МВ = МС. Опустим из точки М перпендикуляр МО на плоскость АВС (рис. 35.3). Докажем, что точка О — центр описанной окружности треугольника АВС. Поскольку 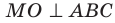
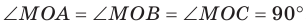
Заметим, что когда надо определить расстояние между двумя геометрическими фигурами, то стремятся найти расстояние между их ближайшими точками. Например, из курса планиметрии вы знаете, что расстоянием от точки, не принадлежащей прямой, до этой прямой называют расстояние от данной точки до ближайшей точки на прямой, то есть длину перпендикуляра, опущенного из точки на прямую. Теорема 35.1 показывает, что целесообразно принять следующее определение.
Определение. Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
Пример:
Докажите, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости.
Решение:
Пусть А и В — две произвольные точки прямой 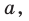
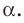
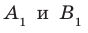
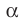
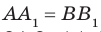
По теореме 34.3 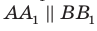
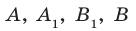
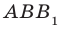
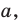
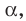
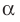
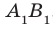
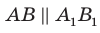
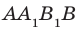
Доказанное свойство позволяет принять следующее определение. Определение. Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости. Используя результат, полученный в ключевой задаче 2, можно решить следующую задачу.
Пример:
Докажите, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Определение. Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
Результаты, полученные в ключевых задачах 2 и 3, часто используют в практической деятельности, например в строительстве (рис. 35.5).
Теорема 35.2 (теорема о трех перпендикулярах). Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Доказательство. Докажем первую часть теоремы.Пусть прямая 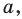
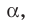
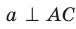
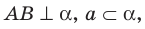
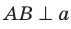
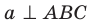
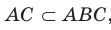
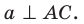
Пример:
Точка М не принадлежит плоскости выпуклого многоугольника и равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость многоугольника является точка О, принадлежащая многоугольнику. Докажите, что точка О — центр вписанной окружности многоугольника.
Решение:
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Опустим из точки О перпендикуляры ON, ОК и ОЕ соответственно на прямые АВ, ВС и СА (рис. 35.7). Соединим точку М с точками Е, К и N.
Отрезок ON является проекцией наклонной MN на плоскость АВС. По построению 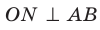
Аналогично можно доказать, что 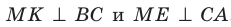
В прямоугольных треугольниках MON, МОК, МОЕ катет МО общий, гипотенузы равны; следовательно, данные треугольники равны по катету и гипотенузе. Из равенства этих треугольников следует, что ON = ОК = ОЕ.
Длины отрезков ON, ОК и ОЕ являются расстояниями от точки О до прямых, содержащих стороны треугольника АВС. Мы показали, что эти расстояния равны. Так как точка О принадлежит треугольнику АВС, то точка О — центр вписанной окружности треугольника АВС.
Угол между прямой и плоскостью
Вы знаете, что в давние времена путешественники ориентировались по звездам. Они измеряли угол, который образовывал с плоскостью горизонта луч, идущий от данной точки к небесному телу.
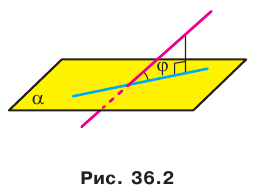
Сегодня человеку в своей деятельности также важно определять углы, под которыми наклонены к данной плоскости некоторые объекты (рис. 36.1). Эти примеры показывают, что целесообразно ввести понятие угла между прямой и плоскостью.
Определение. Если прямая параллельна плоскости или принадлежит ей, то считают, что угол меж ду такой прямой и плоскостью равен 0°.
Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 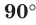
Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость (рис. 36.2).
Из определения следует, что если 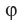
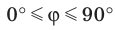
Также принято говорить, что прямая образует угол 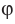
Углом между отрезком и плоскостью называют угол между прямой, содержащей этот отрезок, и плоскостью.
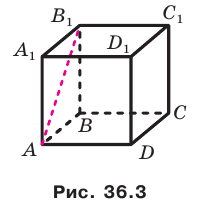
Например, рассмотрим куб 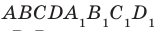
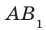
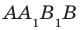
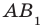
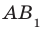
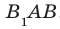
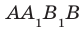
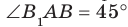
Пример:
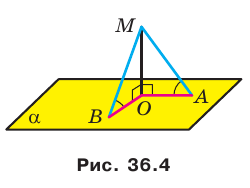
Докажите, что если из одной точки к плоскости проведены наклонные, образующие равные углы с плоскостью, то проекция данной точки на плоскость равноудалена от оснований наклонных.
Решение:
Пусть МЛ и М В — наклонные, образующие с плоскостью 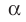
Прямая ОА является проекцией прямой МА на плоскость 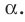
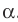
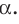
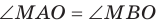
Поскольку 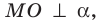
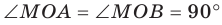
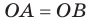
Двугранный угол. Угол между плоскостями
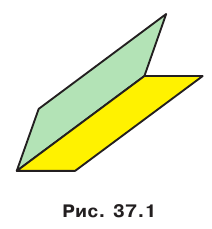
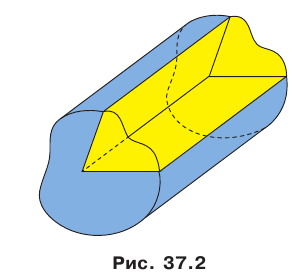
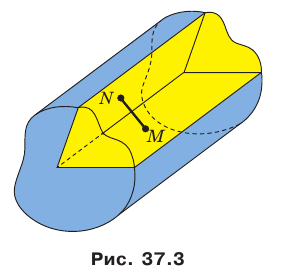
На рисунке 37.1 изображена фигура, состоящая из двух полуплоскостей, имеющих общую границу. Эта фигура делит пространство на две части, выделенные на рисунке 37.2 разными цветами. Каждую из этих частей вместе с полуплоскостями называют двугранным углом. Полуплоскости называют гранями двугранного угла, а их общую границу — ребром двугранного угла. Как видим, «желтый» и «синий» двугранные углы, изображенные на рисунке 37.2, существенно различаются. Это различие выражается следующим свойством. На гранях двугранного угла выберем произвольные точки М и N (рис. 37.3).
Отрезок MN принадлежит «желтому» двугранному углу, а «синему» двугранному углу принадлежат лишь концы отрезка. В дальнейшем, говоря «двугранный угол», будем подразумевать такой двугранный угол, который содержит любой отрезок с концами на его гранях («желтый» двугранный угол).
Наглядное представление о двугранном угле дают полуоткрытая классная доска, двускатная крыша, открытый ноутбук (рис. 37.4).
Двугранный угол считают пространственным аналогом угла на плоскости. Вы знаете, как определяют величину угла на плоскости. Научимся определять величину двугранного угла.
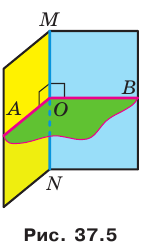
Отметим на ребре MN двугранного угла произвольную точку О. Через точку О в гранях двугранного угла проведем лучи ОА и ОВ перпендикулярно ребру MN (рис. 37.5). Угол АОВ, образованный этими лучами, называют линейным углом двугранного угла. Поскольку 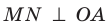
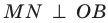
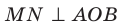
Определение. Величиной двугранного угла называют величину его линейного угла.
Двугранный угол называют острым, прямым, тупым или развернутым, если его линейный угол соответственно острый, прямой, тупой или развернутый.
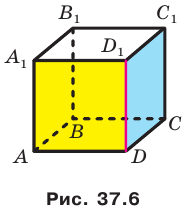
Например, рассмотрим куб 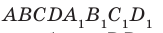
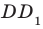
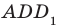
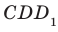
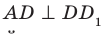
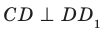
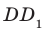
Угол ADC прямой.
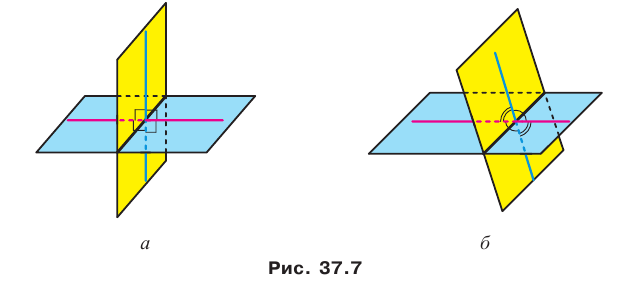
При пересечении двух плоскостей образуются четыре двугранных угла, отличных от развернутого (рис. 37.7). Здесь возможны два случая:
- все четыре двугранных угла прямые (рис. 37.7, а);
- из четырех двугранных углов два равных угла острые и два равных угла тупые (рис. 37.7, б).
В обоих случаях из четырех двугранных углов найдется такой, величина которого не превышает 90°.
Определение. Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°. Угол между двумя параллельными плоскостям и равен 0°.
Углом между многоугольником и плоскостью, которой много угольник не принадлежит, называют угол между плоскостью, содержащей многоугольник, и данной плоскостью.
Углом между двумя многоугольниками, лежащими в разных плоскостях, называют угол между плоскостями, в которых лежат эти многоугольники.
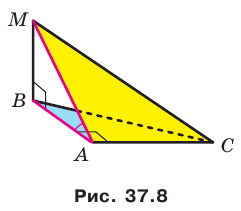
Пример:
Прямоугольные треугольники 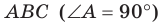
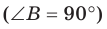
Решение:
Отрезок ВА является проекцией наклонной МА на плоскость АВС. Так как 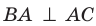
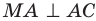
Для стороны AM прямоугольного треугольника АМС можно записать: 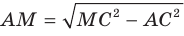
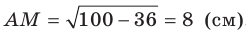
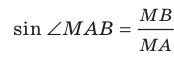
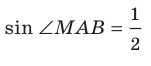
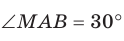
Имеет место теорема, устанавливающая связь между площадью данного многоугольника и площадью его проекции.
Теорема 37.1 (площадь ортогональной проекции многоугольника). Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где 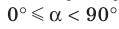
Определение. Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Если плоскости 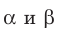
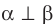
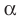
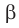
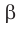
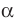
Наглядное представление о перпендикулярных плоскостях дают плоскости стены и потолка комнаты, плоскости двери и пола, плоскости сетки и теннисного корта (рис. 37.9).
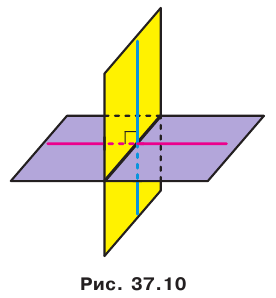
Очевидно, что перпендикулярные плоскости при пересечении образуют четыре прямых двугранных угла (рис. 37.10).
Теорема 37.2 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
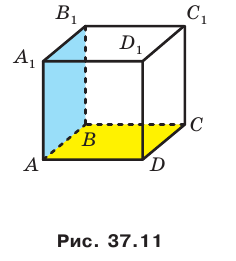
Например, плоскость грани 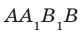
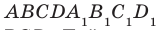
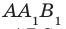
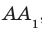

Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает 90°. Считают, что угол между двумя параллельными прямыми равен 0°. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Перпендикулярность прямой и плоскости
- Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
- Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
- Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
- Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
- Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
Ортогональная проекция фигуры
Пусть фигура 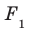
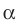
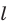
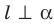
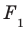
Расстояние от точки до плоскости
Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
Расстояние от прямой до параллельной ей плоскости
Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости.
Расстояние между двумя параллельными плоскостями
Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
Теорема о трех перпендикулярах
Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Угол между прямой и плоскостью
- Если прямая параллельна плоскости или принадлежит ей, то считают, что угол между такой прямой и плоскостью равен 0°.
- Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 90°.
- Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость.
Величина двугранного угла
Величиной двугранного угла называют величину его линейного угла.
Угол между двумя пересекающимися плоскостями
Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°.
Площадь ортогональной проекции многоугольника
Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где
Перпендикулярные плоскости
Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Признак перпендикулярности плоскостей
Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Векторы и координаты в пространстве
- Множества
- Рациональные уравнения
- Рациональные неравенства и их системы
- Предел числовой последовательности
- Предел и непрерывность числовой функции одной переменной
- Функции, их свойства и графики
- Параллельность в пространстве
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📺 Видео
Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

§51 Уравнение прямой в пространстве, проходящей через две точкиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Лекция 28. Виды уравнения прямой в пространстве.Скачать

Параметрические уравнения прямойСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Уравнение прямой в пространстве. 11 класс.Скачать