Параметр а1 в уравнении тренда построенному по прямолинейной функции характеризует средний за период (2 видео)

Ответы на тесты по теме Статистика

Содержание

Тенденция во временном ряду
Линейный тренд
Параметры тренда
Оценка параметров уравнения тренда
💥 Видео

Для более эффективного поиска следует вводить 2-3 ключевых слова из вопроса .

уравнение тренда имеет вид у = 66,61+7,57 t на сколько в среднемежегодно изменялся анализируемый показатель

увеличивался на 7,57

Остатки модели тренда — это

разность между фактическим и теоретическим значениями уровней ряда

Остатки модели тренда – это

продлением в будущее.

—> для выравнивания временного ряда характеризующего изменение количества машин в автопарке за ряд лет, использовано уравнение тренда вида Y=a+bt. Параметр b характеризует

срдний годовой абсолютный прирост

при прогнозировании на основе уравнения тренда в качестве значения независимой переменной используется

порядковый номер периода на который.

по данным о динамике ВВП России за 11 лет (в млрд дол по ППС) получено уравнение тренда y=1815,41+167,95t чему равен прогноз объема ВВП по уравнению на следуюзий период

3662,86( не правильно) 3830,81

прогнозирование на основе урвнения тренда возможно, если

выполняются все перечисленные условия

при каком из ниже приведенных значений t что параметр модели тренда значим

Задача. На основе временного ряда показателей оборота малых предприятий в России за период с 2009 по 2014 годы получена модель тренда: y=15958,27+1815,40*t Величина стандартной ошибки оценивания — 810. 12 млрд.руб.

28666,07 млрд. руб

По данным о динамике ВВП США в период с 2000 по 2014 года построена линейная модель тренда: y=9806,37+498,84*t

Значение x x x 353,93

Задача. По данным о динамике ВВП США в период с 2000 по 2014 годы построена линейная модель тренда y=9806.37 + 498.84 * t и получены значения характеристик (192,31 21,15 69675677 125265)

Значение X X 556,23 X

Для выравнивания временного ряда, характеризующего изменение количества машин в автопарке за ряд лет, использовано уравнение тренда вида: Y=a+bt. Параметр b характеризует

средний годовой абсолютный прирост

выполняются все перечисленные условия

средний годовой абсолютный прирост

При каком из ниже приведенных значений t — статистики можно утверждать, что параметр модели тренда статистически значим:

Остатки модели тренда – это:

разность между фактическими и теоретическими значениями уровней ряда

По данным о динамике ВВП России за 11 лет (в млрд. дол. по ППС) получено уравнение тренда: yt=1815,41+167,95t. Чему равен прогноз объема ВВП по уравнению на следующий период

По данным о динамики ВВП США в период с 2000 по 2014 годы построена линейная модель тренда: и получены значения характеристик:

Задача. На основе временного ряда показателей оборота малых предприятий в России за период с 2009 по 2014 годы получена модель тренда:

Видео:Теория автоматического регулирования. Лекция 5. Модели параметров состоянийСкачать

Тенденция во временном ряду

Синонимом тенденции в эконометрике является тренд. Одним из наиболее популярных способов моделирования тенденции временного ряда является нахождение аналитической функции, характеризующей зависимость уровней ряда от времени. Этот способ называется аналитическим выравниванием временного ряда.

Зависимость показателя от времени может принимать разные формы, поэтому находят различные функции: линейную, гиперболу, экспоненту, степенную функцию, полиномы различных степеней. Временной ряд исследуют аналогично линейной регрессии.

Параметры любого тренда можно определить обычным методом наименьших квадратов, используя в качестве фактора время t = 1, 2,…, n, а в качестве зависимой переменной используют уровни временного ряда. Для нелинейных трендов сначала проводят процедуру линеаризации.

К числу наиболее распространенных способов определения типа тенденции относят качественный анализ изучаемого ряда, построение и анализ графика зависимости уровней ряда от времени, расчет основных показателей динамики. В этих же целях можно часто используют и коэффициенты автокорреляции уровней временного ряда.

Видео:Прогнозирование в Excel с помощью линий трендаСкачать

Линейный тренд

Тип тенденции определяют путем сравнения коэффициентов автокорреляции первого порядка. Если временной ряд имеет линейный тренд, то его соседние уровни yt и yt-1 тесно коррелируют. В таком случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть максимальный. Если временной ряд содержит нелинейную тенденцию, то чем сильнее выделена нелинейная тенденция во временном ряду, тем в большей степени будут различаться значения указанных коэффициентов.

Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить перебором основных видов тренда, расчета по каждому уравнению коэффициента корреляции и выбора уравнения тренда с максимальным значением коэффициента.

Параметры тренда

Наиболее простую интерпретацию имеют параметры экспоненциального и линейного трендов.

Параметры линейного тренда интерпретируют так: а — исходный уровень временного ряда в момент времени t = 0; b — средний за период абсолютный прирост уровней рада.

Параметры экспоненциального тренда имеют такую интерпретацию. Параметр а — это исходный уровень временного ряда в момент времени t = 0. Величина exp(b) — это средний в расчете на единицу времени коэффициент роста уровней ряда.

По аналогии с линейной моделью расчетные значения уровней рада по экспоненциальному тренду можно определить путем подстановки в уравнение тренда значений времени t = 1,2,…, n, либо в соответствии с интерпретацией параметров экспоненциального тренда: каждый последующий уровень такого ряда есть произведение предыдущего уровня на соответствующий коэффициент роста

При наличии неявной нелинейной тенденции нужно дополнять описанные выше методы выбора лучшего уравнения тренда качественным анализом динамики изучаемого показателя, для того, чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом ряду поворотных точек и изменения темпов прироста, начиная с определенного момента времени под влиянием ряда факторов, и т. д. В том случае если уравнение тренда выбрано неправильно при больших значениях t, результаты прогнозирования динамики временного ряда с использованием исследуемого уравнения будут недостоверными по причине ошибки спецификации.

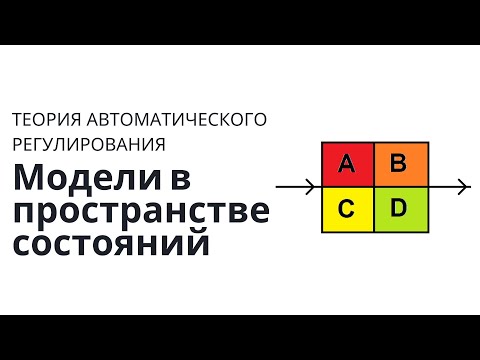
Иллюстрация возможного появления ошибки спецификации приведем на рисунке

Если оптимальной формой тренда является парабола, в то время как на самом деле имеет место линейная тенденция, то при больших t парабола и линейная функция естественно будут по разному описывать тенденцию в уровнях ряда.

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.

Видео:Excel. Линия трендаСкачать

Оценка параметров уравнения тренда

При использовании полиномов разных степеней оценка параметров уравнения тренда производится методом наименьших квадратов (МНК) точно так же, как оценки параметров уравнения регрессии на основе пространственных данных. В качестве зависимой переменной рассматриваются уровни динамического ряда, а в качестве независимой переменной – фактор времени t, который обычно выражается рядом натуральных чисел 1, 2, . п.

Оценка параметров нелинейных функций проводится МНК после линеаризации, т.е. приведения их к линейному виду. Рассмотрим применение МНК для некоторых нелинейных функций, которые не излагались подробно в главе, посвященной регрессии.

Для оценки параметров показательной кривой у = ab1 или экспоненты у = еа+ы (либо у = аеы) путем логарифмирования функции приводятся к линейному виду lny = ln a + t ln b или экспоненты: lny = a + bt. Далее строится система нормальных уравнений

(5.21)

Пример 5.1

Число зарегистрированных ДТП (на 100 000 человек населения) по Новгородской области за 2000–2008 гг. характеризуется данными:

Исходя из графика была выбрана показательная кривая / Для построения системы нормальных уравнений были рассчитаны вспомогательные величины

Система нормальных уравнений составила

Решая ее, получим значения

Соответственно имеем экспоненту или показательную кривую

За период с 2000 по 2008 г. число дорожно-транспортных происшествий возрастало в среднем ежегодно на 13,5%. Экспонента достаточно хорошо описывает тенденцию исходного временного ряда: коэффициент детерминации составил 0,9202. Следовательно, данный тренд объясняет 92% колеблемости уровней ряда и лишь 8% ее связаны со случайными факторами.

Некоторую специфику имеет оценка параметров кривых с насыщением: модификационной экспоненты, логистической кривой, кривой Гомперца, гиперболы вида По этим функциям должна быть сначала определена асимптота. Если она может быть задана исследователем на основе анализа временного ряда, то другие параметры могут быть оценены по МНК. В этих случаях данные функции приводятся к линейному виду. Рассмотрим оценку параметров этих кривых на отдельных примерах, начиная с модифицированной экспоненты.

Пример 5.2

Уровень механизации труда (в %) характеризуется динамическим рядом (табл. 5.2)

Таблица 5.2. Расчет параметров модифицированной экспоненты у = с ab’t

Так как уровень механизации труда не может превышать 100%, то имеется объективно заданная верхняя асимптота с = 100. Для оценки параметров а и b приведем рассматриваемую функцию к линейному виду ; обозначим (с-у) через Y и прологарифмируем:

Далее применим МНК и получим систему нормальных уравнений

Для нашего примера, исходя из данных итоговой строки табл. 3, имеем систему уравнений

Решив ее, получим ln а = 3,06311; ln b = -0,19744. Соответственно потенцируя, получим: т.е. уравнение .

Если перейти от Y к исходным уровням ряда, уравнение модифицированной экспоненты составит , где параметр показывает средний коэффициент снижения уровня использования ручного труда за 1998–2005 гг. Расчетные значения у, т.е. могут быть найдены путем подстановки в уравнение 0,8208′ соответствующих значений t. Либо на основе уравнения In 7= 3,06311 – 0,19744 г при компьютерной обработке определяется In У и далее 100 – е 1пу. Так, при t = 8 In Y = = 1,48363 и 100 – e1’48363 = 100 – 4,40892 = 95,59108 = 95,6 (см. последнюю графу таблицы). Ввиду некоторой смещенности оценок (так как МНК применяется к логарифмам) Ху, Ф Ху,, хотя в примере эти величины достаточно близки друг другу.

Если асимптота с не задана, то оценка параметров модифицированной экспоненты усложняется. В этих случаях могут использоваться разные методы оценивания: метод трех сумм, метод трех точек [1] , с помощью регрессии [2] , метод Брианта [3] . Рассмотрим применение метода регрессии для оценки параметров модифицированной экспоненты вида у = с – abc.

Пример 5.3

В таблице представлены данные о расходах предприятия на рекламу за 10 мес. года.

Таблица 5.3. Данные о расходах предприятия на рекламу за 10 мес. года (в тыс. руб.)

Найдем по нашему ряду цепные абсолютные приростыг и представим их через параметры нашей функции, T.e.z = c-ab’ – с + ab’

l = ab’ 1 (1 – b). Известно, что для модифицированной экспоненты логарифм абсолютных приростов линейно зависит от фактора времени t. Следовательно, можно записать, что lnz = Ιηα + (f – 1) lnb + ln(l – b). Обозначим Ιηα + ln(l – b) через d. Тогда lnz = d + (t- 1) lnb, т.е. линейное в логарифмах уравнение. Применяя МНК, получим оценки параметров d, lnb, а соответственно и параметра Ь. В рассматриваемом примере на основании граф табл. 5.3 lnz и (t – 1) было найдено уравнение регрессии: lnz = 4,519641 – 0,20882 (t – 1). Исходя из него получаем lnb = -0,20882; b = 0,811538. 4,519641 = In a + In (1 – b) = In [α (1 – b)]. Тогда α (1 – b) = e4,519641, откуда параметра =91,80264/(1-0,811538) = 487,1145.

Далее можно найти оценку параметра с как среднее значение из величин с = у + ab’, найденных для каждого месяца (см. последнюю графу табл. 5.3). Предельная величина расходов на рекламу составит 516,4 тыс. руб. Искомое уравнение тренда примет вид

Рассмотренный метод применим, если абсолютные приросты – величины положительные. Если же некоторые приросты окажутся меньше нуля, то нужно проводить сглаживание уровней временного ряда методом скользящей средней.

Для логистической кривой Перла – Рида аналогично параметры а и b могут быть найдены МНК, если асимптота с задана. Тогда данная функция преобразовывается в линейную из логарифмов обозначим через Y и прологарифмируем, т.е. ). Далее параметры а и b определяются МНК, как и в примере по табл. 5.3.

Для логистической кривой вида параметры а и b могут быть оценены МНК, если асимптота с задана, так как в этом случае функция линеаризуема: ; обозначим через Y величину и прологарифмируем : Далее, применяя МНК, оцениваем параметры а и b.

При практических расчетах значение верхней асимптоты логистической кривой может быть определено исходя из существа развития явления, различного рода ограничений для его роста (нормативы потребления, законодательные акты), а также графически.

Если верхняя асимптота не задана, то для оценки параметров могут использоваться разные методы: Фишера, Юла, Родса, Нейра и др. Сравнительная оценка и обзор этих методов изложены в работе E. М. Четыркина [4] .

Покажем на примере расчет параметров логистической кривой по методу Фишера.

Пример 5.4

Производство продукции характеризуется данными, представленными в табл. 5.4.

Таблица 5.4. Расчет параметров логистической кривой

Метод Фишера основан на определении производной для логистической кривой. Дифференцируя данную функцию по t, получим уравнение

Обозначим темп прироста логистической кривой через . Тогда , т.е. для z, имеем линейную функцию с параметрами а и . Чтобы найти решение, необходимо оценить z,. Предполагая, что интервалы между уровнями в ряду динамики равны, Фишер предложил приближенно оценивать в виде уравнения , где п — 1. Для нашего примера значения z, представлены в графе 3 табл. 5.4. Далее применяем МНК к уравнению : , т.е. строим регрессию z( оту(, беря данные от t = 2 до f = 8. Уравнение регрессии запишется в виде Исходя из него находим параметры а и с для логистической кривой. Параметр а = 0,806. Данное уравнение статистически значимо: F-критерий равен 689,6; R2 = 0,996. Соответственно для него значимы и параметры: f-критерий для параметра а равен 47,2 и для параметра – равен -26,2. Так как , то и т.е. верхняя асимптота производства продукции составляет 403 ед.

После того, как найдены параметры а и с, находим параметр b. Для этого функциюпредставим как Обозначим через Y выражение в левой части равенства, т.е..-Тогда имеем уравнение Прологарифмируем его:. В этом уравнении свободным членом является In Ь. Его можно определить из первого уравнения системы нормальных уравнений, а именно Для нашего примера имеем уравнение . Соответственно Таким образом, логистическая кривая запишется в виде

Теоретические значения данной функции представлены в графе 6 табл. 5.4 (найдены путем подстановки соответствующих значений t). Они достаточно близко подходят к исходным данным: коэффициент корреляции между ними равен 0,999; ввиду того, что в расчетах использовались логарифмы. Если предположить, что предельное значение объема производства продукции равно 400 ед., т.е. применить МНК к уравнению , то получим и b = =67,5; параметр а при компьютерной обработке определяется как -а = -0,8. Соответственно уравнение тренда запишется в виде . Результаты двух уравнений достаточно близки.

Параметры кривой Гомперца также могут быть оценены МНК, если асимптота с задана, так как в этом случае данная функция сводима к линейному виду Прологарифмировав ее, получим уравнение .

Вторично прологарифмировав, получим уравнение , Обозначив через у*, lgb через В и Ig(lga) через А, запишем кривую Гомперца в линейном виде , для оценки параметров которой применим МНК.

При практическом применении кривой Гомперца могут возникнуть некоторые сложности по динамическому ряду с повышающейся тенденцией. В этом случае задается верхняя асимптота с и логарифмы При повторном логарифмировании в расчетах используются лишь положительные значения Продемонстрируем возможность оценки параметров кривой Гомперца с верхней асимптотой на примере динамики по предприятию товарных запасов на начало каждого месяца (тыс. долл.).