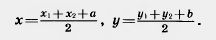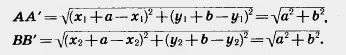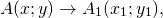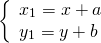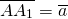Параллельный перенос и его свойства
- Содержание
- Общие сведения о параллельном переносе
- Свойства параллельного переноса
- Повторение темы о параллельном переносе
- Свойства, которыми обладает параллельный перенос в пространстве
- Истрия и применение в науке
- Примеры из жизни
- Параллельный перенос в геометрии
- Что такое параллельный перенос
- Свойства, которыми обладает параллельный перенос в пространстве
- Формула параллельного переноса
- Виды параллельного переноса
- Параллельный перенос
- 🔍 Видео
Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Содержание
Видео:11 класс, 12 урок, Параллельный переносСкачать

Общие сведения о параллельном переносе
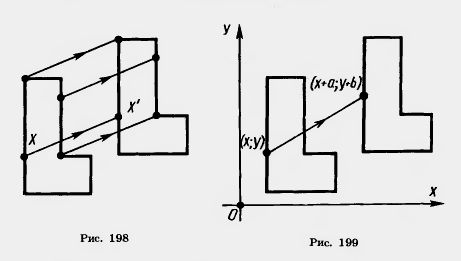
Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение.
Введем на плоскости декартовы координаты х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x’ = x + а, у’ = у + b.
Эти формулы выражают координаты х’, у’ точки, в которую переходит точка (х; у) при параллельном переносе.
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Свойства параллельного переноса
Параллельный перенос есть движение.
Действительно, две произвольные точки А(х1; у1) к В (х2; у2) переходят при параллельном переносе в точки А’ (х1 +а; у1 + b), В'(х2 + а; y2+b). Поэтому
АВ 2 =(х2-х1) 2 + (у2-у1 ) 2
Отсюда АВ=А’В’. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.
Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
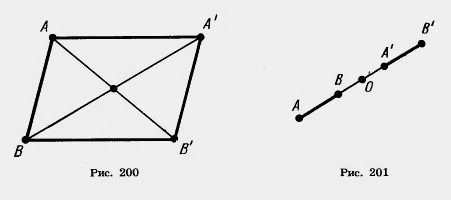
Действительно, пусть точки A (x1; y1) и В (x2; y2) переходят в точки A'(x1+а; y1 + b) и В’ (х2 + а; y2 + b) (рис. 200). Середина отрезка АВ’ имеет координаты
Те же координаты имеет и середина отрезка А’В. Отсюда следует, что диагонали четырехугольника АА’В’В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А’ и ВВ’ параллельны и равны.
Заметим, что у параллелограмма АА’В’В параллельны и две другие противолежащие стороны — АВ и А ‘В’. Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую (или в себя).
Замечание. В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА’. В случае, когда точка В лежит на прямой АА’, точка В’ тоже лежит на этой прямой, так как середина отрезка АВ’ совпадает с серединой отрезка ВА’ (рис. 201). Значит, все точки А, В, А’, В’ лежат на одной прямой. Далее,
Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние 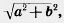
Видео:Видеоурок "Преобразование координат"Скачать

Повторение темы о параллельном переносе
Мы с вами уже познакомились с такой темой, как параллельный перенос. На этом уроке вы узнали, что такое преобразование на плоскости, где все точки перемещаются на одно и то же расстояние, считается параллельным переносом.
Из данного урока, каждому из вас стало понятно, что параллельный перенос является движением, так как при таком переносе любая прямая переходит в такую же параллельную ей прямую.
Если мы посмотрим на рисунок, то можем наглядно представить такое движение, как сдвиг площади в направлении данного вектора на его длину.
Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Свойства, которыми обладает параллельный перенос в пространстве
• Во-первых, параллельный перенос является движением;
• Во-вторых, при выполнении этого действия все точки смещаются по параллельным прямым и притом на одно и то же расстояние;
• В-третьих, при таком переносе прямая имеет свойство переходить в такую же параллельную прямую или в себя саму;
• В-четвертых, независимо от того, какими точками были A и A’, но точка A переходит в точку A’.
• В-пятых, при таком переносе, т.е параллельном переносе в пространстве, в любом случае плоскость имеет свойство переходить в себя саму или же такую же параллельную ей плоскость.
Видео:9 класс, 32 урок, Параллельный переносСкачать

Истрия и применение в науке
Как правило, в каждого понятия есть свой первооткрыватель, но автор параллельного переноса в пространстве, на жаль, нам неизвестен. А вот применение параллельного переноса в пространстве довольно широко. Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии.
Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Примеры из жизни
В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве.
А также, параллельный перенос можно встретить и в таких необычных ситуациях:
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Видео:Поворот и параллельный перенос координатных осей. ЭллипсСкачать
Параллельный перенос в геометрии
Видео:Тема: Движения. Урок: Движения на плоскости. Параллельный переносСкачать

Что такое параллельный перенос
Параллельным переносом называют изменение плоскости со смещением точек в одинаковом направлении на определенное расстояние.
Параллельный перенос строго определяют через декартовы координаты или через вектор. Предположим, что на плоскости имеются декартовы координаты х и у. Сформулируем тогда определение параллельного переноса.
Параллельный перенос представляет собой преобразование фигуры F с переходом какой-то точки с координатами (х;у) в точку с координатами (х+а; у+b), где а и b обозначают некие числа, одинаковые для каждой из точек (х;у), принадлежащих фигуре F.
Далее рассмотрим определение параллельного переноса через вектор.
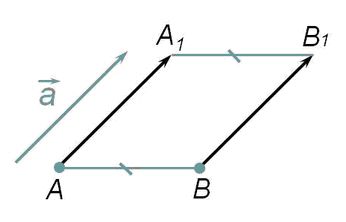
Параллельный перенос на заданный вектор a ¯ является отображением плоскости на саму себя, при котором предусмотрено отображение каждой точки А в такую точку А 1 , что вектор А А 1 соответствует вектору a ¯ :
В рамках некой плоскости выражение параллельного переноса с аналитической точки зрения в прямоугольной системе координат ( x , y ) предусматривает следующее:
( x , y ) ↦ ( x + a , y + b ) ,
Здесь вектор определяется значением:
С помощью параллельного переноса происходит перемещение любой из точек фигуры или пространства на одинаковое расстояние в одинаковом направлении. В качестве доказательства изобразим этот процесс наглядно на примере рисунке:
Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Свойства, которыми обладает параллельный перенос в пространстве
В процессе параллельного переноса можно наблюдать смещение некой фигуры, в том числе, квадрата, относительно параллельных прямых на одинаковое расстояние. При этом возможен переход перпендикулярных прямых в прямые, которые также являются перпендикулярными.
Вместе с тем, параллельные прямые трансформируются в прямые, которые также являются параллельными. Параллельный перенос некой фигуры не сопровождается изменением расстояния, на которое удалены ее точки, и углов между прямыми. Данные характеристики сохраняются без корректировок.
Перечислим характерные свойства, которыми обладает параллельный перенос:
- Параллельный перенос можно определить, как вид движения, то есть в процессе переноса расстояние сохраняется без изменений.
- В процессе параллельного переноса происходит смещение точек по параллелям или прямым, которые совпадают, на одинаковое расстояние.
- Если реализован параллельный перенос, то каждая из прямых перейдет в результате в прямую, которая является ей параллельной, либо в саму себя.
- При любых точках А и А 1 допустим лишь один параллельный перенос, предполагающий переход точки А в точку А 1 .
Примечание
С параллельным переносом можно столкнуться при изучении многих предметов, в том числе, физики и геометрии. Например, в алгебре с помощью параллельного переноса упрощается построение графиков для решения легких и сложных задач в классе.
Видео:Уравнение параллельной прямойСкачать

Формула параллельного переноса
Предположим, что на плоскости, где расположены оси О х и О у , построена фигура. Обозначим ее S . В процессе параллельного переноса можно наблюдать переход каждой из точек рассматриваемой фигуры в точку А’ на одинаковое расстояние.
Из вышесказанного можно сделать вывод о том, что трансформация фигуры S в фигуру S ‘ при смещении каждой из точек фигуры, в том числе, окружности, с координатами х и у в точку с координатами x + a и y + b , где a и b постоянные числа, определяется, как параллельный перенос. Таким образом, параллельный перенос является движением, при котором каждая из точек фигуры перемещается на одинаковое расстояние.
Получить координаты новой фигуры, образованной в результате параллельного переноса, можно с помощью следующих формул:
A B 2 = ( x B — x A ) 2 + ( y B — y A ) 2
A ‘ B ‘ 2 = ( x B ‘ — x A ‘ ) 2 + ( y B ‘ — y A ‘ ) 2
Переход точки A ( x ; y ) в точку A 1 ( x 1 ; y 1 ) при параллельном переносе A ( x ; y ) → A 1 ( x 1 ; y 1 ) можно описать с помощью уравнения:
x 1 = x + a y 1 = y + b
В некоторых литературных источниках можно встреть такую формулировку теоремы, как: точка А 1 представляет собой образ точки А , что возможно при реализации параллельного переноса на вектор ( a ; b ). В таком случае точка A является прообразом.
Видео:Параллельные прямые циркулемСкачать

Виды параллельного переноса
Запишем виды движения в пределах некоторой плоскости:
- параллельный перенос любой фигуры, в том числе, трапеции;
- осевая симметрия;
- поворот вокруг точки;
- центральная симметрия.
При параллельном переносе поступательное движение точек представляет собой перемещение в одинаковом направлении на одинаковое расстояние. Таким образом, происходит отражение фигуры на плоскости. При перемещении точек на одинаковый вектор, данный вектор называют вектором переноса.
Так как параллельный перенос характеризуется свойством, при котором в процессе движения не меняется направление, справедливым является и обратное утверждение. В результате, движение при стабильном направлении можно считать параллельным переносом.
Видео:Свойства параллельного переноса. Геометрия 8 классСкачать

Параллельный перенос
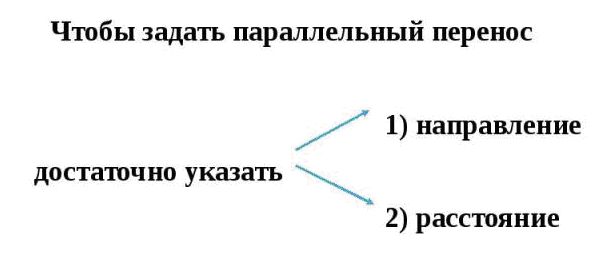
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.
Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.
1) Введём на плоскости декартовы координаты x, y.
Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.
Формулы параллельного переноса

то параллельный перенос задаётся формулами:
Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:
Свойства параллельного переноса
1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).
2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.
В алгебре параллельный перенос широко используется для построения графиков функций.
🔍 Видео
12. Уравнения прямой в пространстве Решение задачСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

9 класс. Параллельный переносСкачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Перенос заданного отрезка на произвольную прямуюСкачать

Решение задач на параллельный перенос в декартовой системе координат. Геометрия 8 классСкачать

Параллельный перенос. Координаты точек при параллельном переносе. Геометрия 8 классСкачать