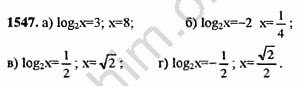Параграф 51 логарифмические уравнения 1547 (7 видео)

Номер 1547 — ГДЗ по алгебре 10-11 класс Мордкович

Вы открыли задание номер 1547 из решебника на uchim.org.

(кликните по решению, если нужно изменить размер)

Введите номер задания:

Чтобы добавить страницу в закладки, нажмите Ctrl+D.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Содержание

51. Логарифмические уравнения
Алгебра
Уравнения вида logaf(x) = logag(x)
Уравнения, требующие предварительных преобразований
Логарифмические уравнения с заменой переменных
Логарифмирование уравнений
Переход от логарифмических неравенств к нелогарифмическим
📸 Видео

Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

51. Логарифмические уравнения

Логарифмическим уравнением называется уравнение, в котором неизвестная величина содержится под знаком логарифма или в его основании.

При решении логарифмических уравнений обязательно учитывается ОДЗ логарифма. Если ОДЗ найти сложно, то можно только выписать условия, а затем проверить полученные корни подстановкой в ОДЗ (можно проверять подстановкой в уравнение, не выписывая ОДЗ).

Типы уравнений и способы их решения

Всюду далее F(X), G(X), H(X) – некоторые выражения с переменной (число).

I тип: уравнение вида

(6.8)

ОДЗ:

На указанной ОДЗ уравнение (6.8) решают по определению логарифма:

II тип: уравнение вида

(6.9)

ОДЗ:

На основании равенства логарифмов, уравнение (6.9) сводится к равносильному ему (на указанной ОДЗ) уравнению:

(6.10)

ОДЗ:

Данное уравнение на ОДЗ равносильно совокупности уравнений:

III тип: уравнения, решаемые заменой переменной

(6.11)

Где F – некоторое выражение относительно

Необходимо определить ОДЗ уравнения, учитывая все условия существования логарифма и выражения F.

Далее заменяют и решают уравнение

Если – корни последнего уравнения, то, после возвращения к старой переменной, необходимо решить совокупность

Полученные корни проверяют по ОДЗ.

З а м е ч а н и е. Если вместо какого-либо выражения F(X), G(X), H(X) уравнения (6.8)–(6.11) содержат число, то соответствующее условие не записывают в ОДЗ.

Пример 1. Решить уравнение

Преобразуем уравнение к виду

Получили уравнение I типа, которое решается по определению логарифма:

Откуда

Из полученных значений корень Х = 4 не подходит по ОДЗ.

Получаем ответ: Х = 6.

Пример 2. Решить уравнение

Решение. Записываем условия, определяющие ОДЗ:

Заданное уравнение относится к I типу. Получаем:

Снова используем определение логарифма:

т. е. откуда

Полученные корни проверяем подстановкой в условия, определяющие ОДЗ уравнения. Убеждаемся, что корень подходит, а корень не подходит по ОДЗ.

Получаем ответ:

Пример 3. Решить уравнение

Решение. Записываем условия, определяющие ОДЗ:

Данное уравнение относится ко II типу, т. е. решается по свойству равенства логарифмов. Получаем:

т. е.

Раскладываем левую часть на множители:

откуда получаем

Подставляем найденные значения в ОДЗ, находим, что уравнение имеет только один корень Х = 3.

В ответе имеем: Х = 3.

Пример 4. Решить уравнение

т. е.

Данное уравнение относится ко II типу. Решаем совокупность:

По ОДЗ подходит только корень Х = 2, так как

Получаем ответ: Х = 2.

Пример 5. Решить уравнение

Решение. ОДЗ: Преобразуем уравнение:

Имеем квадратное уравнение относительно (уравнение III типа). Заменяем

Решая полученное квадратное уравнение, находим корни Возвращаемся к переменной X:

Оба корня подходят по ОДЗ, получаем ответ:

Пример 6. Решить уравнение

Решение. Запишем условия ОДЗ:

Воспользуемся тем, что

Тогда

Решаем полученное уравнение как уравнение I типа:

Среди целых делителей свободного члена находим корень Х = –2. Он подходит по ОДЗ.

Пришли к ответу: Х = –2.

Пример 7. Решить уравнение

Решение. ОДЗ: т. е.

Воспользуемся свойствами модуля: если и Тогда уравнение перепишется в виде

Заменяем и приходим к квадратному уравнению

Корнями которого являются числа

Возвращаемся к старой переменной:

Раскрываем модуль, используя ОДЗ:

Получаем ответ:

Пример 8. Решить уравнение

Решение. ОДЗ: т. е. Х Î R.

Рассмотрим левую часть уравнения:

Преобразуем правую часть. Получим:

Используя функциональный метод решения, заключаем, что решением исходного уравнения является решение системы

т. е. Х = –2.

Получаем ответ: Х = –2.

Пример 9. Найти сумму корней уравнения

Решение. Для данного уравнения характерно следующее: если Х – корень уравнения, то и (–Х) тоже корень уравнения. Поэтому если уравнение имеет корни, то их сумма будет равна нулю. Подстановкой находим корни

Видео:Логарифмические уравнения. 11 класс.Скачать

Алгебра

План урока:

Задание. Укажите корень логарифмического уравнения

Задание. Решите урав-ние

В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид

Задание. Найдите решение логарифмического уравнения

Задание. Решите урав-ние

Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:

Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Уравнения вида log_af(x) = log_ag(x)

Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.

Задание. Решите урав-ние

Задание. Найдите корень урав-ния

Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид

С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.

Задание. Решите урав-ние

Получили квадратное уравнение, которое решаем с помощью дискриминанта:

Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:

Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:

Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log₃ (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).

Видео:Проще простого! Как решить Логарифмическое Уравнение?Скачать

Уравнения, требующие предварительных преобразований

Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду log_af(x) = log_ag(x).

Задание. Решите урав-ние

с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:

Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:

Задание. Решите урав-ние

Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем

Задание. Решите урав-ние

Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log₅ 5. Тогда урав-ние можно преобразовать:

Задание. Решите урав-ние

Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что

Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что

Задание. Решите урав-ние

Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log₂₅x 4 к основанию 5, используя известную нам формулу

Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:

Видео:Логарифмические уравнения 🥷🏿Скачать

Логарифмические уравнения с заменой переменных

Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.

Задание. Решите уравнение методом замены переменной

Задание. Найдите решение уравнения методом замены переменной

Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:

Видео:Логарифмические уравнения. Практическая часть. 11 класс.Скачать

Логарифмирование уравнений

Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.

Задание. Укажите корни урав-ния

Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:

Возвращаемся от переменной t к переменной х:

Видео:Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #ShortsСкачать

Переход от логарифмических неравенств к нелогарифмическим

Рассмотрим график логарифмической функции у = log_ax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства

Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.

Задание. Найдите решение логарифмического неравенства

Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 log_as:

Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 log_a s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение

Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:

Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).