Парабола заданная уравнением y x 3 x 1 пересекает

Алгебра | 5 — 9 классы

Порабола, заданная уравнением y = (x + 3)(x — 1) пересекает ось ox в точках A и B и ось oy в точке C.

Найдите площадь треугольника ABC.

По формуле установим координаты точек А( — 3 ; 0), В(1 ; 0) и С(0 ; — 3).

Высота h треугольника, опущенная на сторону АВ лежит на оси Оу и равна 3.

Основание АВ треугольнка равно 4.

5AB * h = 0, 5 * 4 * 3 = 6.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Написать уравнение параболы, которая пересекает ось абцисс в точках с абсциссами х = 1 и х = 2, а ось ординат в точке с ординатой у = 0, 5?

Написать уравнение параболы, которая пересекает ось абцисс в точках с абсциссами х = 1 и х = 2, а ось ординат в точке с ординатой у = 0, 5.

Видео:Как построить график линейной функции.Скачать

Прямая у = kх + b пересекает ось х в точке(18 ; 0) а ось у в точке (0 ; 9)Запиши уравнение этой прямой?

Прямая у = kх + b пересекает ось х в точке(18 ; 0) а ось у в точке (0 ; 9)Запиши уравнение этой прямой.

Проходит ли эта прямая через точку ( — 16 ; — 12).

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Прямая проходящая через точку ( — 4 — 1) пересекает ось оу в точке (0 3)?

Прямая проходящая через точку ( — 4 — 1) пересекает ось оу в точке (0 3).

Найдите угол наклона этой прямой к положительному направлению оси ох.

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Как найти в какой точке пересекает ось х график функции заданной формулой у = 0, 4х — 12?

Как найти в какой точке пересекает ось х график функции заданной формулой у = 0, 4х — 12.

Видео:Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать

Прямая y = kx + b пересекает ось x в точке (2 ; 0) и ось y в точке (0 ; 7)?

Прямая y = kx + b пересекает ось x в точке (2 ; 0) и ось y в точке (0 ; 7).

Напишите уравнение этой прямой.

Видео:Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Равные отрезки ab и cd пересекаются в точке О так, что О ОА = ОD?

Равные отрезки ab и cd пересекаются в точке О так, что О ОА = ОD.

Докажите, что треугольник АВС = треугольнику ВDC.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

В какой точке график функции, заданной формулой у = х / 3(обыкновенная дробь) + 2 пересекает ось координат ?

В какой точке график функции, заданной формулой у = х / 3(обыкновенная дробь) + 2 пересекает ось координат ?

Видео:Известно, что парабола проходит через точку В(-1; -1/40, и её вершина находится в начале координатСкачать

Запишите уравнение прямой, параллельной у = — 1 / 4х, и , пересекающей ось Оу в точке (0 ; — 4)?

Запишите уравнение прямой, параллельной у = — 1 / 4х, и , пересекающей ось Оу в точке (0 ; — 4).

Видео:Парабола. Квадратичная функцияСкачать

Постройте график уравнения 3х — 2у = 5 в какой точке уравнения пересекает : а) ось абсцисс б) ось ординат?

Постройте график уравнения 3х — 2у = 5 в какой точке уравнения пересекает : а) ось абсцисс б) ось ординат?

Видео:Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

В какой точке пересекаются ось абсцисс и ось симмет рии графика функции у = х2 + 4х — 5?

В какой точке пересекаются ось абсцисс и ось симмет рии графика функции у = х2 + 4х — 5?

Вы перешли к вопросу Порабола, заданная уравнением y = (x + 3)(x — 1) пересекает ось ox в точках A и B и ось oy в точке C?. Он относится к категории Алгебра, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Алгебра. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Это первое задание)))).

1) 100 * 3 = 300 км — пройденный путь шоссе 2) 60 * 2 = 120 км — пройденный путь грунтовая дорога 3) 300 + 120 = 420 км — весь пройденный путь 4) 3 + 2 = 5 часов — он ехал 5) 420 : 5 = 84 км / ч Ответ : средняя скорость автомобиля 84 км / ч.

1. а) 15в / с ^ 3 б) 5 (y — 2) * (y — 1) * (y + 1) / (y + 1) * (y — 2)(y + 2) = (5y — 5) / (y + 2) 2. (x — 3) ^ 2 * 4a ^ 2 / 8a ^ 3 * (x — 3)(x + 3) = (x — 3) / 2a (x + 3).

Видео:Парабола. Квадратичная функция. Как строить?Скачать

Квадратичная функция. Построение параболы

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Видео:Как построить график функции без таблицыСкачать

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 в частном случае при b = 0, c = 0:

Точки, обозначенные фиолетовыми кружками, называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

x

y

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x

y

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля (a 2 + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1. Если D 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
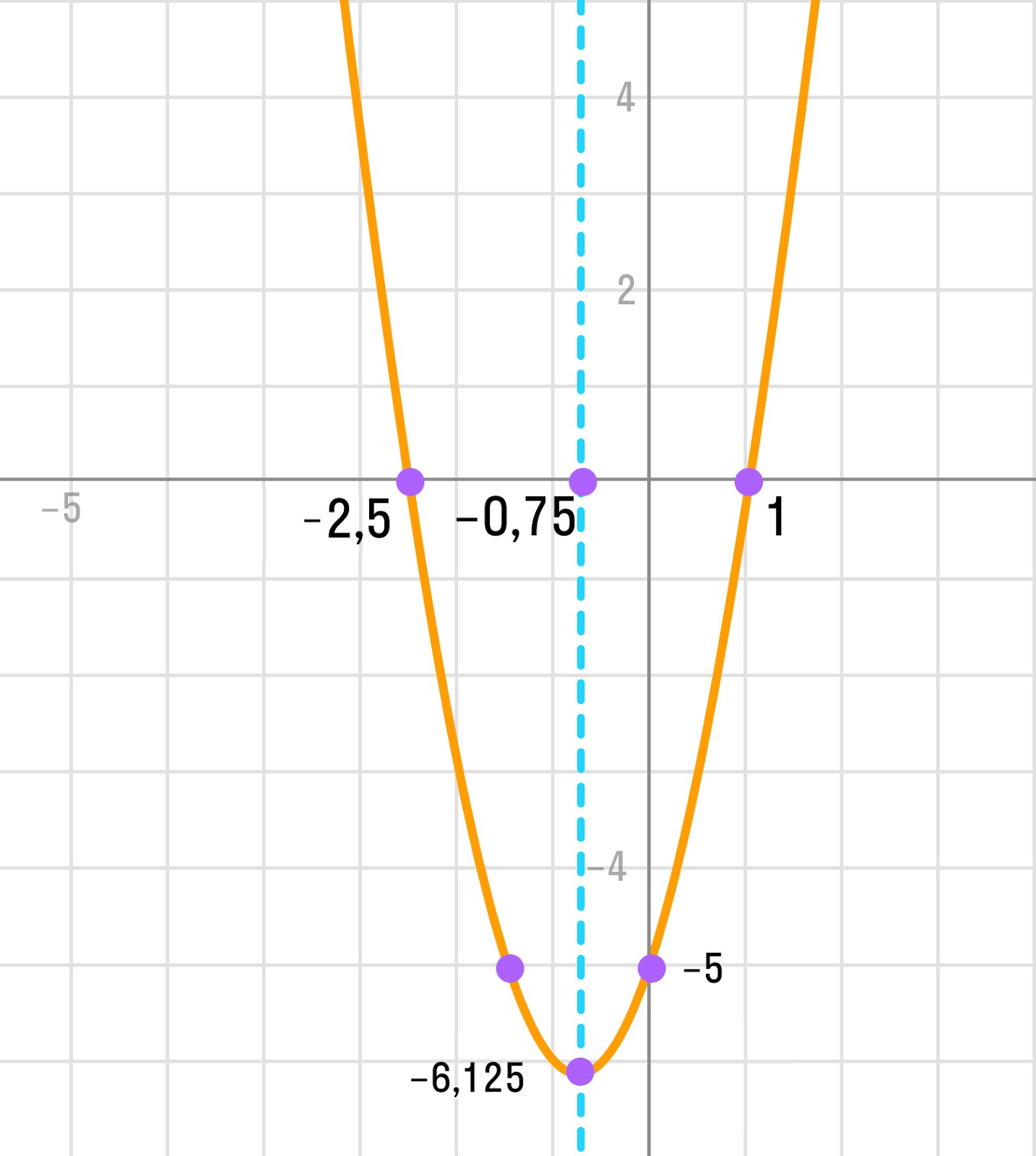
2. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Видео:Построить график функции y=x2. Парабола.Скачать

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Видео:Как легко составить уравнение параболы из графикаСкачать

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.

Нанесем эти точки на координатную плоскость и построим график параболы:

Видео:Функция y=x³ и ее график. 7 класс.Скачать

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x₀) + y₀, где x₀, y₀ — координаты вершины параболы.

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

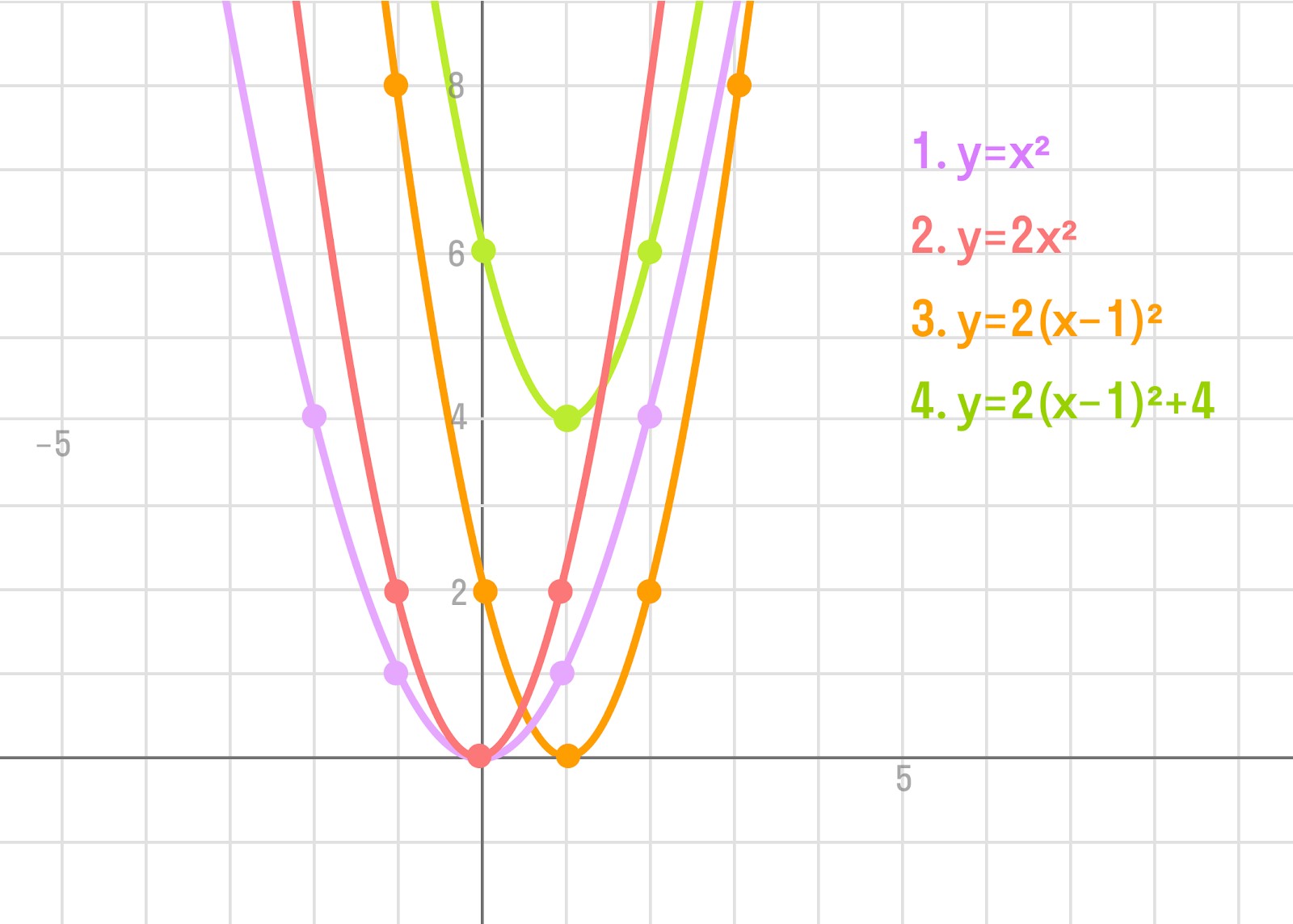
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить график функции y = x 2 ,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

Построить график параболы для каждого случая.



Видео:График функции y=x² (y=аx).Скачать



Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид функции позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:



Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.

Отметим эти точки на координатной плоскости и соединим плавной прямой линией.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать



докажите что парабола y=2x^2-5x+1 и прямая 2x+y+3=0 не пересекаются



2x^2 -5x+1 = -2x-3
2x^2 -3x+4=0
D = 9 -4*4*2 вещественных корней нет ==> не пересекаются



докажите что парабола y=2x^2-5x+1 и прямая 2x+y+3=0 не пересекаются

y=2x^2-5x+1 и у=-2х-3
Две функции пересекаются, если
2х-5х+1=-2х-3
2х-5х+1+2х+3=0
2х-3х+4=0
Д=(-3)-4*2*4=9-16=-7
т.к. Д

📽️ Видео

Парабола / квадратичная функция / влияние коэффициентовСкачать