Парабола изображенная на координатной плоскости задается уравнением у х2 6х 9 а прямые уравнениями (7 видео)

Гипербола,изображенная на координатной плоскости,задаётся уравнением у=8_х, а

Гипербола,изображенная на координатной плоскости,задаётся уравнением у=8_х, а прямые-уравнениями у=-2х-8,у=5х+4,у=-4х+3,у=4х-2

Сирятский Степка
Математика 2019-07-24 07:41:37 0 1

РЕШЕНИЕ на рисунке в прибавленьи.

1) Прямые с положительным коэффициентом — 1) и 3) — имеют две точки скрещения.

2) Остается проверить две иные — 2) и 4).

y = 8/x = — 2*x — 8 — решаем

— 2*x — 8*x — 8 = — (x+2) = 0 Корень: Х = -2

Содержание

Задание №11 ОГЭ по математике
Теория к заданию №11
Разбор типовых вариантов задания №11 ОГЭ по математике
Первый вариант задания (параболы)
Второй вариант задания (гиперболы)
Третий вариант задания (линейный график)
Парабола на координатной плоскости. Решение квадратных неравенств
Парабола на координатной плоскости
Решение квадратных неравенств
🔍 Видео

Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Задание №11 ОГЭ по математике

В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями.

Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.

Задание 11 несложное, тем не менее последние задания придуманы таким образом, чтобы любознательным школьникам было над чем подумать.

Ответом в задании 10 является набор цифр, описывающий соответствие между различными объектами.

Теория к заданию №11

Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.

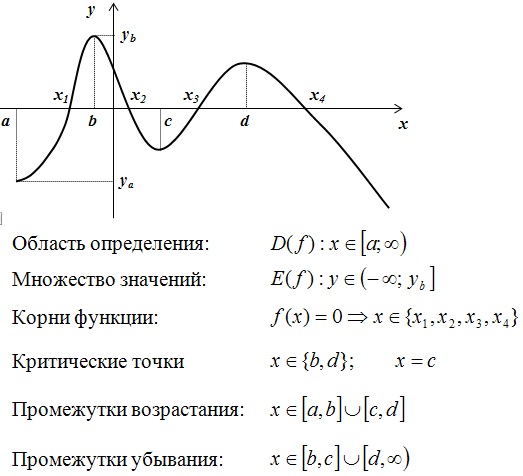
На произвольном примере ознакомимся с исследованием функции:

область определения и множество значений
корни и критические точки
промежутки возрастания убывания

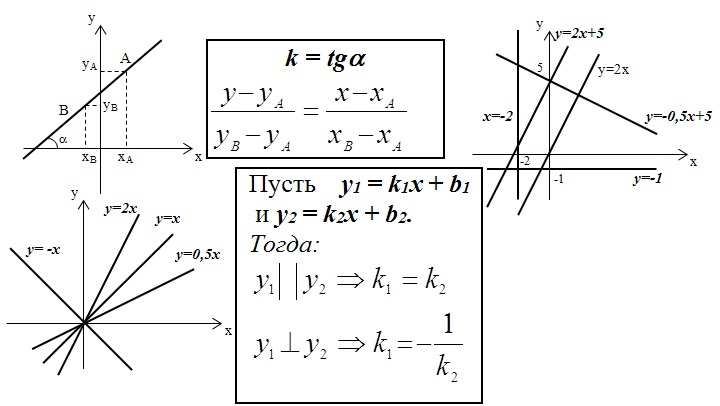
Теперь рассмотрим данный материал на линейной функции:

y = kx + b

где k – угловой коэффициент, b – свободный член

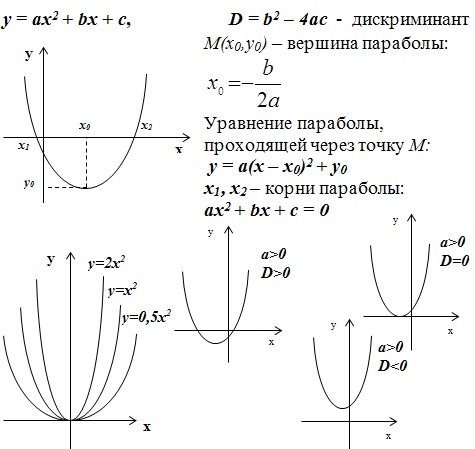
Рассмотрим случай квадратичной функции:

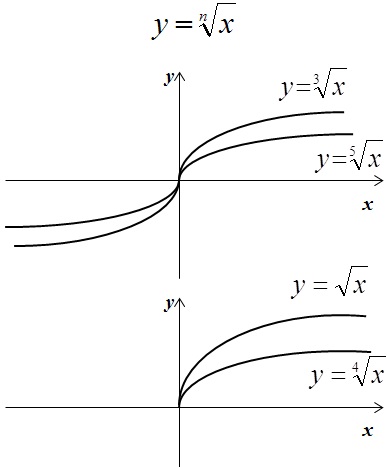
Также вспомним, что такое коренная функция и модуль:

Я разобрал три случая — случай с параболой и влияние коэффициентов на вид параболы — в первом примере. Во втором примере разобрана гипербола и общие закономерности зависимости общего вида графика от математического выражения. Третий случай рассматривает прямую и варианты её построения в зависимости от коэффициентов.

Разбор типовых вариантов задания №11 ОГЭ по математике

Первый вариант задания (параболы)

На рисунках изображены графики функций вида

Установите соответствие между знаками коэффициентов a и c и графиками функций.

В) a > 0, c 0, то ветви направлены вверх, а если a 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

Из всего вышеперечисленного можно найти ответ:

Второй вариант задания (гиперболы)

Установите соответствие между функциями и их графиками.

Решение:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

Третий вариант задания (линейный график)

Установите соответствие между функциями и их графиками.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Парабола на координатной плоскости.
Решение квадратных неравенств

Парабола изображенная на координатной плоскости задается уравнением у х2 6х 9 а прямые уравнениями

Парабола на координатной плоскости

Решение квадратных неравенств

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Парабола на координатной плоскости

Определение 1 . Параболой называют график функции

y = a x 2 ,

(1)

где a – любое число, не равное нулю. Точку О (0;0) называют вершиной параболы (1).

При a > 0 и a график функции (1) изображён на рисунках 1 и 2 соответственно.

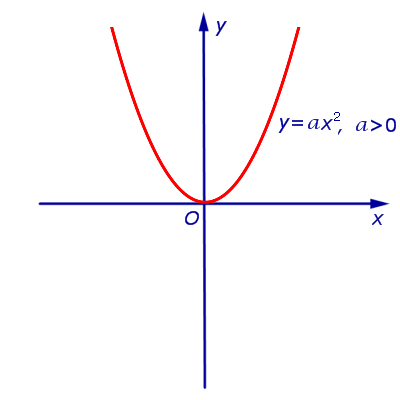Рис.1

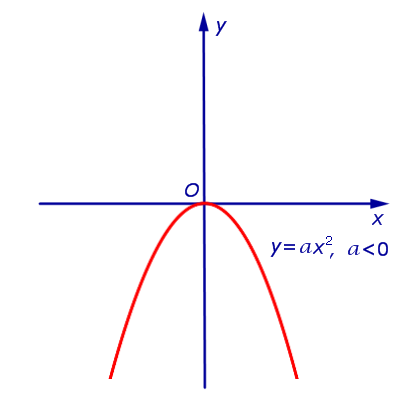Рис.2

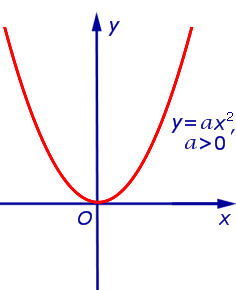Рис.1

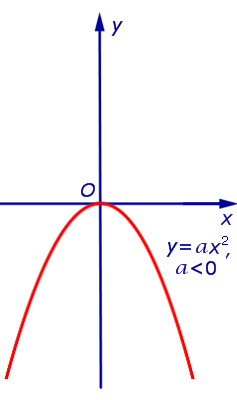Рис.2

Функция (1) обладает следующими свойствами :

областью определения функции функции (1) является вся числовая ось;
функция (1) является четной функцией, поскольку для всех значений аргумента выполнено равенство

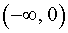при a > 0 функция (1) убывает на интервале и возрастает на интервале ;
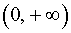при a функция (1) возрастает на интервале 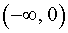и убывает на интервале ;

при a > 0 у функции (1) существует единственныйминимум на всей области определения, который достигается в точке x = 0 ;

при a у функции (1) существует единственныймаксимум на всей области определения, который достигается в точке x = 0 ;

при a > 0 ветви параболы (1) направлены вверх;

при a ветви параболы (1) направлены вниз;

и при a > 0 , и при aвершиной параболы (1) является начало координат;

и при a > 0 , и при aосью симметрии параболы (1) является ось ординат.

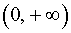Рассмотрим теперь функцию, заданную формулой

y = a x 2 + b x + c ,

(2)

где a, b, c – любые числа, но число a не равно нулю.

Поскольку выражение, стоящее в правой части формулы (2), является квадратным трёхчленом, то, в соответствии с материалом, изложенным в разделе «Квадратные уравнения», формулу (2) можно переписать в виде

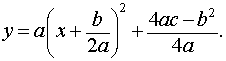(3)

Из формулы (3) вытекает, что график функции (2) может быть получен из графиков, изображенных на рисунках 1 или 2 (в зависимости от знака числа a ) при помощи параллельного переноса, в результате которого вершина параболы (1) передвигается из начала координат в точку V (рис. 3, 4) с координатами

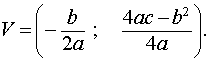(4)


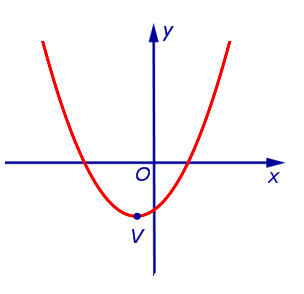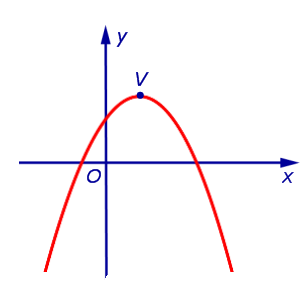Рис.3	Рис.4

Рис.3

Рис.4

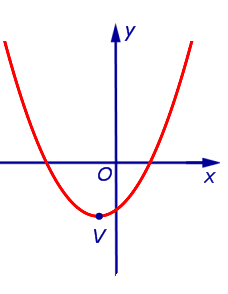Рис.3

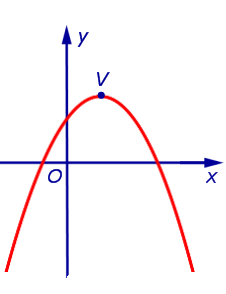Рис.4

D = b 2 – 4ac ,

(5)

то координаты вершины параболы (3), определяемые по формуле (4), можно записать так:

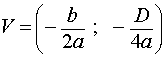(6)

Замечание . При a > 0 ветви параболы (2) направлены вверх, при a ветви параболы (2) направлены вниз. Парабола (2) пересекает ось ординат в точке с координатами (0; c) .

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать