Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы имеет вид:

где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.
На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.
В математическом анализе принята другая запись уравнения параболы:
то есть ось параболы выбрана за ось координат. Можно заметить, что ax² — это квадратный трёхчлен ax² + bx + c , в котором b = 0 и c = 0 . График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.
Фокус параболы имеет координаты
Директриса параболы определяется уравнением 
Расстояние r от любой точки 

Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.
Пример 1. Определить координаты фокуса параболы
Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае — в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:
Находим координаты фокуса параболы:
Пример 2. Составить уравнение директрисы параболы
Решение. Находим p:
Получаем уравнение директрисы параболы:
Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.
Решение. Параметр p — это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:
Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.
Парабола обладает следующим оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.
Видео:213. Фокус и директриса параболы.Скачать

2.5 Парабола
Парабола Есть геометрическое место точек на плоскости, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Выберем систему координат таким образом (рисунок 2.7): за ось ОХ примем прямую, проходящую через фокус F перпендикулярно к директрисе, за положительное направление примем направление от директрисы к фокусу. За начало координат примем середину О отрезка от точки F до директрисы, длину которого обозначим через Р и будем называть параметром параболы. Пусть М(Х, У) произвольная точка, лежащая на параболе. Пусть точка N основание перпендикуляра, опущенного из М На директрису. По определению параболы MN = MF.
Из этого условия получаем Каноническое уравнение параболы в выбранной системе координат
Пусть P > 0, исследуем форму параболы.
Из канонического уравнения параболы видно, что Х не может принимать отрицательных значений, т. е. все точки параболы лежат справа от оси ОY. Уравнение содержит переменную У В квадрате, значит парабола симметрична относительно оси ОХ, эта ось называется Осью Параболы. Точка О пересечения параболы с ее осью симметрии называется Вершиной параболы.
Для параболы, заданной уравнением (2.11), вершина совпадает с началом координат, а ось симметрии – с осью ОХ. График параболы имеет вид, изображенный на рисунке 2.7. Уравнение директрисы записывается в виде 
Фокус параболы для параболы с осью симметрии – осью Х имеет вид F(

Определяет параболу, область определения которой 
Имеет вершину в начале координат, фокус 

Пример 2.4. Составить уравнение параболы и ее директрисы, зная, что она симметрична относительно оси ОY, фокус находится в точке F(0; 2), вершина совпадает с началом координат.
Решение. Будем искать уравнение параболы в виде Х2 = 2Py, так как по условию она симметрична относительно оси OY.
По условию 
Видео:Фокус и директриса параболы 2Скачать

Задача 31453 Пожалуйста помогите 1)определить.
Условие
Пожалуйста помогите
1)определить величину параметра расположение относительно координатных оси следующих парабол: y^2=6x x^2=5y
2)найти фокус и уравнение директрисы параболы y^2=24x
Решение
Канонические уравнения параболы:
x^2=2py cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
Фокус F(0;p/2)
Уравнение директрисы:
y=-p/2
x^2=-2py cимметрична относительно оси Оу, ветви направлены в сторону противоположную оси Оу
Фокус F(0;-p/2)
Уравнение директрисы:
y= p/2
y^2=2px cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(p/2;0)
Уравнение директрисы:
x=-p/2
y^2=-2px cимметрична относительно оси Ох, ветви направлены в сторону противоположную оси Ох
Фокус F(-p/2;0)
Уравнение директрисы:
x=p/2
[b]Решение[/b]:
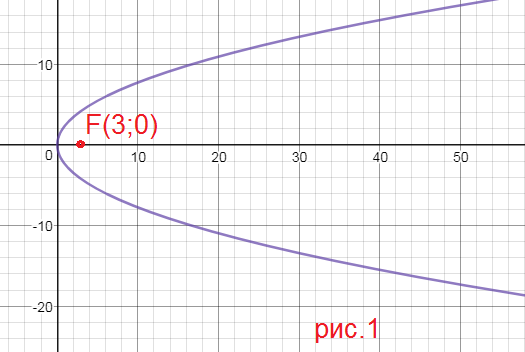
1) y^2=6x ⇒ 2p=6;
p=3
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
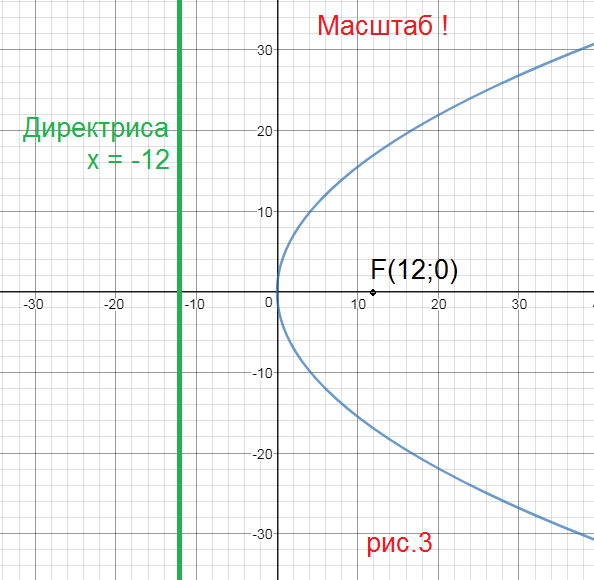
x^2=5y 2p=5 ⇒ 2p=5;
p=2,5
cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
2)
y^2=24x ⇒ 2p=24;
p=12
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(12;0)
Уравнение директрисы:
x=-12
см. рис.3 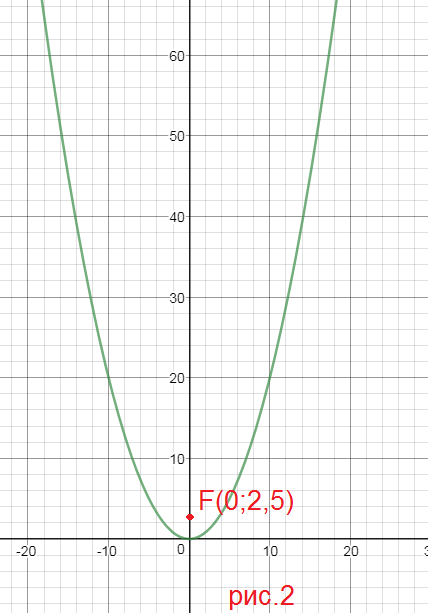
🔥 Видео
Как легко составить уравнение параболы из графикаСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Построение параболы по ее директрисе и фокусуСкачать

Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Как найти вершину параболы?Скачать

Фокус и директриса параболы 1Скачать

Фокус и директриса параболы 2Скачать

Уравнение параболы #алгебра #графики #парабола #репетиторСкачать

Видеоурок "Парабола"Скачать

Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Парабола | Элементы аналитической геометрииСкачать

8 класс. Найти координаты точек пересечения параболы с осями координатСкачать

Фокус и директриса параболы 2Скачать

Фокус и директриса параболы 2Скачать

Функция у=х^2. ПАРАБОЛА. §11 алгебра 8 классСкачать