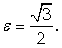Пара пересекающихся прямых с уравнением (4 видео)

Исследование уравнений второго порядка

Содержание

Преобразование координат в уравнении второго порядка.
Канонические виды уравнений второго порядка.
Случай A’C’ > 0.
Случай A’C’ Определение.
Случай (A’C’ = 0).
Оптическое свойство кривых второго порядка. Касательные к эллипсу и гиперболе
5.2.8. Примеры решения задач по теме «Кривые 2-го порядка»
📸 Видео

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Преобразование координат в уравнении второго порядка.

В общей декартовой системе координат линия второго порядка может быть задана уравнением
$$
Ax^ + 2Bxy + Cy^ + 2Dx + 2Ey + F = 0,label
$$
в котором коэффициенты (A), (B) и (C) не равны нулю одновременно. Исследуем множество точек, которые ему удовлетворяют, не предполагая заранее, что хоть одна такая точка существует. С этой целью мы будем менять систему координат так, чтобы уравнение стало возможно проще. С самого начала можно считать систему координат декартовой прямоугольной, так как при переходе к прямоугольной системе координат общий вид уравнения eqref не изменится.

При повороте базиса декартовой прямоугольной системы координат на угол (varphi) старые координаты точки (x), (y) будут связаны с ее новыми координатами (x’), (y’) формулами
$$
x = x’cos varphi-y’sin varphi,\ y = x’sin varphi + y’cos varphi.nonumber
$$
В новых координатах уравнение eqref примет вид
$$
A(x’cos varphi-y’sin varphi)^ + 2B(x’cos varphi-y’sin varphi) times \ times (x’sin varphi + y’cos varphi) + C(x’sin varphi + y’cos varphi) + … = 0.nonumber
$$
Здесь многоточием обозначены члены первой степени относительно (x’), (y’) и свободный член, которые нет необходимости выписывать. Нас будет интересовать член с произведением (x’y’) в преобразованном уравнении. В невыписанные члены это произведение не входит, и мы подсчитаем, что половина коэффициента при (x’y’) есть
$$
B’ = -Asin varphi cos varphi + B(cos^varphi-sin^varphi) + Csin varphi cos varphi.nonumber
$$
Если (B = 0), то поворачивать систему координат не будем. Если же (B neq 0), то выберем угол (varphi) так, чтобы (B’) обратилось в нуль.

Это требование приведет к уравнению
$$
2B cos 2varphi = (A-C)sin 2varphi.label
$$
Если (A = C), то (cos 2varphi = 0), и можно положить (varphi = pi/4). Если же (A neq C), то выбираем (varphi = displaystylefrac operatorname left[fracright]). Для нас сейчас важно то, что хоть один такой угол обязательно существует. После поворота системы координат на этот угол линия будет иметь уравнение
$$
A’x’^ + C’y’^ + 2D’x’ + 2E’y’ + F’ = 0.label
$$
Выражения для коэффициентов уравнения eqref через коэффициенты eqref подсчитать не трудно, но это не нужно. Теперь коэффициент при произведении переменных равен нулю, а остальные члены мы по-прежнему считаем произвольными.

Если в уравнение eqref входит с ненулевым коэффициентом квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси можно обратить в нуль член с первой степенью этой координаты.

В самом деле, пусть, например, (A’ neq 0). Перепишем eqref в виде
$$
A’left(x’^ + fracx’ + frac<D’^><A’^>right) + C’y’^ + 2E’y’ + F’-frac = 0.nonumber
$$
Если мы сделаем перенос начала координат, определяемый формулами (x″ = x’ + D’/A’), (y″ = y’), то уравнение приведется к виду
$$
A’x″^ + C’y″^ + 2E’y″ + F″ = 0,nonumber
$$
как и требовалось.

Видео:Параллельные прямые | Математика | TutorOnline Скачать

Канонические виды уравнений второго порядка.

Предположим, что (A’C’ neq 0), то есть оба коэффициента отличны от нуля. Согласно утверждению 1 при помощи переноса начала координат уравнение приведется к виду
$$
A’x″^ + C’y″^ + F″ = 0.label
$$

Могут быть сделаны следующие предположения относительно знаков коэффициентов в этом уравнении.

Случай A’C’ > 0.

Если (A’C’ > 0), то коэффициенты (A’) и (C’) имеют один знак. Для (F″) имеются следующие три возможности.

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением eqref при условии (a geq b), называется эллипсом, уравнение называется каноническим уравнением эллипса, а система координат — его канонической системой координат.

При (a = b) уравнение eqref есть уравнение окружности радиуса (a). Таким образом, окружность — частный случай эллипса.

Знак (F″) совпадает с общим знаком (A″) и (C″). Тогда аналогично предыдущему мы можем привести уравнение к виду
$$
frac<x″^><a^> + frac<y″^><b^> = -1,label
$$
Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, которое приводится к каноническому виду eqref, называется уравнением мнимого эллипса.

(F″ = 0). Уравнение имеет вид
$$
a^x″^ + c^y″^ = 0.label
$$
Ему удовлетворяет только одна точка (x″ = 0), (y″ = 0). Уравнение, приводящееся к каноническому виду eqref, называется уравнением пары мнимых пересекающихся прямых. Основанием для этого названия служит сходство с приведенным ниже уравнением eqref.

Случай A’C’ Определение.

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением eqref, называется гиперболой, уравнение называется каноническим уравнением гиперболы, а система координат — ее канонической системой координат.

Случай (A’C’ = 0).

Допустим теперь, что (A’C’ = 0), и, следовательно, один из коэффициентов (A’) или (C’) равен нулю. В случае необходимости, делая замену eqref, мы можем считать, что (A’ = 0). При этом (C neq 0), так как иначе порядок уравнения был бы меньше двух. Используя утверждение 1, мы приведем уравнение к виду
$$
C’y″^ + 2D’x″ + F″ = 0.nonumber
$$

Пусть (D’ neq 0). Сгруппируем члены следующим образом:
$$
C’y″^ + 2D’left(x″ + fracright) = 0.nonumber
$$
Перенесем начало координат вдоль оси абсцисс в соответствии с формулами перехода (x^ = x″ + F″/2D’), (y^ = y″). Тогда уравнение примет вид
$$
C″y^ + 2D’x^ = 0,nonumber
$$
или
$$
y^ = 2px^,label
$$
где (p = -D’/C″). Мы можем считать, что (p > 0), так как в противном случае можно сделать дополнительную замену координат, изменяющую направление оси абсцисс: (tilde = -x^), (tilde = y^).

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением eqref при условии (p > 0), называется параболой, уравнение называется каноническим уравнением параболы, а система координат — ее канонической системой координат.

Допустим, что (D’ = 0). Уравнение имеет вид (C’y″^ + F″ = 0). Относительно (F″) есть следующие три возможности.

Если (C’F″ 0) знаки (C’) и (F″) совпадают. Разделив на (C’), приведем уравнение к виду
$$
y″^ + a^ = 0.label
$$
Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, приводящееся к каноническому виду eqref, называют уравнением пары мнимых параллельных прямых.
Остался последний случай (F″ = 0). После деления на (C’) уравнение принимает вид
$$
y″^ = 0.label
$$
Это уравнение эквивалентно уравнению (y″ = 0), и потому определяет прямую линию. Уравнение, приводящееся к каноническому виду eqref, называется уравнением пары совпавших прямых.

Теперь мы можем объединить всё вместе.

Пусть в декартовой системе координат задано уравнение второго порядка eqref.

Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов:

Уравнение эллипса.
$$
frac<x^><a^> + frac<y^><b^> = 1;nonumber
$$
Мнимый эллипс. Данному уравнению не удовлетворяет ни одна точка.
$$
frac<x^><a^> + frac<y^><b^> = -1;nonumber
$$
Уравнение пары мнимых пересекающихся прямых (точка).
$$
a^x^ + c^y^ = 0;nonumber
$$
Уравнение гиперболы.
$$
frac<x^><a^>-frac<y^><b^> = 1;nonumber
$$
Пересекающиеся прямые.
$$
a^x^-c^y^ = 0;nonumber
$$
Уравнение параболы.
$$
y^ = 2px;nonumber
$$
Пара параллельных прямых.
$$
y^-a^ = 0;nonumber
$$
Пара мнимых параллельных прямых. Данному уравнению не удовлетворяет ни одна точка.
$$
y^ + a^ = 0;nonumber
$$
Прямая (пара совпавших прямых).
$$
y^ = 0.nonumber
$$

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Оптическое свойство кривых второго порядка. Касательные к эллипсу и гиперболе

По этой ссылке вы найдёте полный курс лекций по математике:

Предположим для определенности, что точка М0 лежит в первой четверти, т. е. х0 > О, Уо > 0. Тогда часть эллипса, лежащую в первой четверти, можно описать уравнением Пользуясь формулой (1), получаем уравнение касательной к эллипсу в точке Мо а так как точка (я0, уо) лежит на эллипсе, то Пусть mq(xо, уо) — точка эллипса и, значит, Полученное соотношение после несложных преобразований можно записать так: Отсюда с учетом тождества приходим к уравнению.

Оптическое свойство кривых второго порядка Касательные к эллипсу и гиперболе Касательные к параболе Оптическое свойство эллипса Оптическое свойство гиперболы Оптическое свойство параболы классификация кривых второго порядка Многочлены второй степени на плоскости Канонические уравнения кривых второго порядка (рис. 28). Полученное соотношение является уравнением касательной к эллипсу, проходящей через его точку (я0, Уо), и в обшем случае ее произвольного расположения, т.е. прилюбыхзнаках яо и у0. .

Уравнение касательной к гиперболе выводится аналогично и имеет следующий вид Подчеркнем, что точка (xq, Уо) лежит на гиперболе. Если кривая задана уравнением то уравнение касательной к ней, проходящей через точку (х0,у0), где уо = f(xо), можно записать в следующем виде Касательные к параболе Если кривая задана уравнением то уравнение касательной к ней, проходящей через точку (хо,2/о)> ГДе х0 = д(уо), можно записать в следующем виде Пусть Л/о(х0, уо) — точка параболы.

Пользуясь формулой (I), получаем уравнение касательной к параболе Отсюда в силу равенства yl = 2рх0 приходим к уравнению касательной вида Замечание. Сопоставляя канонические уравнения эллипса, гиперболы и параболы с уравнениями касательных к этим кривым, нетрудно заметить, чтодля получения последних не требуется специальных вычислений.

В самом деле, заменяя у2 на 3/3/0» а х2 на xxq (в случае параболы 2х нужно заменить на х + хо). приходим к уравнению соответствующей касательной. Еше раз отметим, что сказанное справедливо лишь в том случае, когда точка (го. Уо) лежит на кривой. 6.3. Оптическое свойство эллипса Пусть Мо — произвольная точка эллипса Как уже отмечалось, расстояния от нее до фокусов F„ и Fn — фокальные радиусы — равны соответственно.

Проведем через точку А/0 касательную к эллипсу, и вычислим, на каком расстоянии от этой касательной лежат фокусы Fn(

c, 0) и Fn(c, 0) (напомним, что для этого следует воспользоваться формулой (10) из §11.1). Имеем соответственно или — нормирующий м ножитель (рис. 29). Нетрудно проверить,что В самом деле, Обратившись к рис.29, заметим, что вычисленные отношения равны синусам углов, образованных касательной и фокальными радиусами точки касания.

Из того, что синусы этих углов равны, вытекает равенство и самих углов. Тем самым доказано оптическое свойство эллипса: касательная к эллипсу образует равные углы с фокальными радиусами точки касания. Это свойство называется оптическим по следующей причине: если поместить в один из фокусов эллипса с зеркальной «поверхностью» точечный источник Рис.29 света, то все лучи после отражения от «поверхности» эллипса сойдутся в другом его фокусе (рис. 30).

Оптическое свойство гиперболы Устанавливается аналогичными выкладками и заключается в следующем. Если поместить водин из фокусов гиперболы точечный источниксвета,то каждый луч после отражения от зеркальной «поверхности» гиперболы видится исходящим из другого фокуса (рис. 31). Оптическое свойство параболы Если в фокус параболы помешен точечный источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси параболы (рис.32).

Многочлены второй степени на плоскости Теорема. Пусть на плоскости введена прямоугольная декартова система координат Оху и пусть Оптическое свойство кривых второго порядка Касательные к эллипсу и гиперболе Касательные к параболе Оптическое свойство эллипса Оптическое свойство гиперболы Оптическое свойство параболы классификация кривых второго порядка Многочлены второй степени на плоскости Канонические уравнения кривых второго порядка — многочлен второй степени от переменных х и у.

Тогда на плоскости можно построить прямоугольную дека ртов у систему координат O’XY так, что после замены переменных х и у на переменные X uY исходный многочлен f(x, у) приведется к многочлену F(X, Y) одного из следующих трех видов: шаг. Поворотом координатных осей на подходящим образом выбранный угол всегда можно добиться того, чтобы коэффициент при произведении разноименных координат обратился в нуль. Пусть 6^0 (при этот шаг не нужен).

Возможно вам будут полезны данные страницы:

Повернем оси координат вокругточки О. Эта операция описывается следующими формулами Рис.33 При этом координатные оси исходной системы Оху поворачиваются на угол ^ (рис.33). Заменим переменные х и у в формуле (I) их выражениями (2) через и вычислим коэффициент 2b при произведении Он равен и обращается в нуль, если Так как полученное уравнение разрешимо относительно , то указанным преобразованием всегда можно добиться обращения в нуль нужного коэффициента.

Приступая ко второму этапу преобразования, будем считать, что исходный многочлен /(я, у) уже имеет вид где а2 + с2 >0.

Для определенности положим с Ф 0 (это не ограничивает общности наших рассуждений, так как заменой я и у в случае необходимости этого всегда можно добиться). 2-й шаг. Переносом начала координат можно достичьдальнейшего упрощения вида м ногочле-на f(x, у). Эта операция описывается следующими формулами: координатные оси новой системы получаются из координатных осей исходной системы Оху параллельным переносом в точку (-а, -р) (рис.34). Укажем конкретные значения а и р. Возможны три случая Тогда, полагая Рис. 34 О) е получаем глс .

Домножснием обеих частей уравнения из п. I на -1 и заменой X на У, а У на в случае необходимости) всегда можно добиться того, чтобы Полагая получим гиперболу Полагая получим — пару пересекающихся прямых: Название можно объяснить некоторым сходством этого уравнения с уравнением эллипса. Название можно объяснить некоторым сходством этого уравнения с уравнением лары пересекающихся прямых.

Всегда можно добиться того, чтобы В D (заменив, в случае необходимости, X на -X). Полагая получим параболу . Можно считать, что В 0. 1. Е Полагая получим — пару параллельных прямых. 2. Е > 0. Полагая получим На действительной плоскости нет ни одной точки, координаты которой обращали бы это уравнение (пары мнимых пара>1лелыыхпрямых) в тождество. 3. Е = 0. Тогда — пара совпадающих прямых. Чтобы определить тип кривой второго порядка, не обязательно проводить все указанные выше преобразования. Достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.

Оптическое свойство кривых второго

порядка Касательные к эллипсу и гиперболе Касательные к параболе Оптическое свойство эллипса Оптическое свойство гиперболы Оптическое свойство параболы классификация кривых второго порядка Многочлены второй степени на плоскости Канонические уравнения кривых второго порядка уравнение линии второго порядка. Введем следующие обозначения Числа D и Д не зависят от выбора системы координат на плоскости и называются инвариантами.

Из приводимой таблицы видно, какому сочетанию знаков определителей D и Д соответствует та или иная линия второго порядка. Задача. Убедитесь в том, что d и Д при рассмотренных преобразованиях системы координат действительно остаются неизменными. ^ Название можно объяснить некоторым сходством этого уравнения с уравнением пары параллельных Эллипс Мнимый эллипс Пара мнимых пересекающихся прямых Гипербола Пара пересекающихся прямых Парабола Пара параллельных прямых Пара мнимых параллельных прямых Парасовпадаюших прямых

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Геометрия для студентов часть 3Скачать

5.2.8. Примеры решения задач по теме «Кривые 2-го порядка»

Определить тип уравнения кривой 2-го порядка:

Если L1·L2 > 0, то уравнение эллиптического типа;

Если L1·L2 0, следовательно, перед нами уравнение эллиптического типа.

В уравнении отсутствует произведение Ху, следовательно, квадратичная форма его старших членов имеет канонический вид; поэтому коэффициенты при Х2 и У2 являются собственными числами матрицы квадратичной формы. Итак, L1 = 4, L2 = 9, L1·L2 > 0, следовательно, перед нами уравнение эллиптического типа.

Геометрические образы, определяемые уравнением эллиптического типа:

— пустое множество («мнимый эллипс»).

Для приведения уравнения к каноническому виду нужно исключить из него слагаемые. Содержащие первые степени переменных. Для этого преобразуем левую часть:

Зададим параллельный перенос осей координат:

Тогда в новых координатах уравнение примет вид:

Каноническое уравнение эллипса.

Ответ: уравнение эллипса, канонический вид .

Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:

Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.

Геометрические образы, определяемые уравнением гиперболического типа:

— пара пересекающихся прямых.

Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.

Геометрические образы, определяемые уравнением гиперболического типа:

— пара пересекающихся прямых.

Заметим, что для данного уравнения нет необходимости искать явный вид преобразования координат, приводящего квадратичную форму к каноническому виду. Это связано с тем, что уравнение не содержит линейных членов, а его свободный член не изменится при преобразовании вида

Найденные собственные числа будут коэффициентами при Х2 и У2 для канонического вида квадратичной формы. Следовательно, в соответствующей координатной системе уравнение примет вид:

Каноническое уравнение гиперболы.

Ответ: уравнение гиперболического типа, канонический вид

Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:

Перед нами полное уравнение 2-го порядка, и для приведения его к каноническому виду потребуется провести оба преобразования координатных осей: поворот на такой угол, чтобы новые оси стали параллельными собственным векторам матрицы квадратичной формы (это преобразование квадратичной формы к каноническому виду), и параллельный перенос.

Итак, тип уравнения – гиперболический.

Матрица перехода к новому базису:

Собственные векторы следует выбирать так, чтобы определитель матрицы перехода равнялся +1 – при этом не нарушается взаимное расположение координатных осей.

Запишем исходное уравнение в новых координатах:

2) Параллельный перенос:

В новых координатах получаем уравнение

Пара пересекающихся прямых.

Ответ: уравнение гиперболического типа, определяет пару пересекающихся прямых, канонический вид: У″ = ± 2Х″.

Не проводя преобразования координат, установить, что уравнение

Определяет прямую, и найти уравнение этой прямой.

Обратите внимание на то, что квадратичная форма, образованная старшими членами уравнения, является полным квадратом.

Иногда привести уравнение к простому виду удается с помощью алгебраических приемов. Представим левую часть уравнения в виде:

Ответ: уравнение определяет прямую Х – 3У + 2 = 0.

Эллипс, симметричный относительно осей координат, проходит через точки

Найти его эксцентриситет.

По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид, а во-вторых, полуось А равна абсциссе точки А.

По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид:

А во-вторых, полуось А равна абсциссе точки А, т. е. А = 6. Найдем B, подставив в уравнение эллипса координаты точки М:

Итак, уравнение эллипса:

Тогда расстояние от фокуса до начала координат

Вычислим эксцентриситет эллипса:

Ответ: эксцентриситет

Составить уравнение эллипса, фокусы которого лежат на прямой У + 6 = 0, эксцентриситет равен , а точка М(3; -1) является концом малой полуоси.

Найдите расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.

Найдем расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Нормальный вид уравнения данной прямой: -у – 6 = 0, тогда

Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.

Поскольку прямая F1F2 параллельна оси абсцисс, прямая МО параллельна оси ординат; следовательно, ее уравнение: Х = 3. Тогда координаты точки О:

С учетом расположения осей эллипса можно утверждать, что в системе координат, полученной параллельным переносом начала координат в точку

О(3; -6), то есть заданной преобразованием

Уравнение эллипса имеет канонический вид:

Найдем А из условия, что

Подставим найденные значения А и B в уравнение эллипса:

Ответ: уравнение эллипса: Х2 + 2У2 – 6Х + 24У + 31 = 0.

Составить уравнения директрис гиперболы.

Приведите уравнение гиперболы к каноническому виду и составьте уравнения директрис в виде

Приведем уравнение гиперболы к каноническому виду:

Осями симметрии являются координатные оси, А = 3, B = 4. Тогда

Ответ: уравнения директрис:

Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса

Найдите вначале координаты вершин и фокусов эллипса, а затем определите коэффициенты А и B в каноническом уравнении гиперболы.

Координаты вершин гиперболы: (А; 0) и (-А; 0), координаты фокусов: (С; 0) и (–С; 0). Соответственно координаты вершин эллипса: (А1; 0) и (-А1; 0), координаты фокусов: (С1; 0) и (-С1; 0). У данного эллипса А1 = 5,

Тогда для гиперболы А = 4, С = 5, откуда

И уравнение гиперболы:

Ответ:

Составить уравнение касательной к гиперболе

В ее точке М=<15; 4>.

Найдите вначале координаты нормали к гиперболе в точке М (если кривая задана уравнением F(X,Y) = 0, То нормаль к ней в точке М0=<Х0;у0>

Имеет координаты: П = (F′X(X0;Y0);F′Y(X0;Y0))), а затем составьте уравнение прямой, проходящей через точку М=<15; 4> перпендикулярно

Найдем координаты нормали к гиперболе в точке М.

Уравнение прямой, проходящей через точку М0(х0;у0) перпендикулярно вектору П = <A, B>, имеет вид:

А(х – х0) + В(у – у0) = 0.

Запишем уравнение касательной:

Ответ: Уравнение касательной:

Составить уравнение параболы, если даны ее фокус F(2; -1) и директриса

Используйте определение параболы: параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.

Используем определение параболы:

Параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.

Пусть точка М(Х, У) лежит на параболе. Тогда ее расстояние до фокуса

Выразим через Х и У расстояние от точки М до директрисы.

Нормальное уравнение директрисы:

Из определения параболы DM = MF,

Ответ: уравнение параболы: Х2 + 2Ху + У2 – 6Х + 2У + 9 = 0.

Составить уравнение параболы с вершиной в начале координат, если известно, что парабола симметрична относительно оси Ох и проходит через точку А=. Найти координаты ее фокуса.

Из условий задачи следует, что данная парабола задается каноническим уравнением

Подставьте в это уравнение координаты точки А и найдите значение параметра Р параболы.

Из условий задачи следует, что данная парабола задается каноническим уравнением

Подставим в это уравнение координаты точки А: 36 = 2Р·9, откуда Р = 2.

Следовательно, уравнение параболы имеет вид: У2 = 4Х.

Координаты фокуса параболы задаются формулой: F=<0,5P; 0>, то есть F=.

Ответ: уравнение параболы: У2 = 4Х; фокус F=.