Пара корень уравнения у кх

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Функция y=k/х — свойства, график и примеры решения задач

Видео:Математика 5 класс. Уравнение. Корень уравненияСкачать

Общие сведения

Функцией называется некоторая зависимость переменных друг от друга. В некоторых случаях неизвестные величины могут быть выражены системой конкретных значений, интервалами, а также другими функциональными выражениями. Последний класс называется сложным или составным. Различают зависимые и независимые переменные (аргументы). Второй тип может принимать любые значения, кроме тех, которые превращают выражение в неопределенность.

Однако аргументы необходимо также обследовать, поскольку они могут обратить тождество в пустое множество. Одним из таких примеров является функция у = к / х. Ее аргумент x может принимать любые значения, кроме 0. Именно это число превращает уравнение в неопределенность, поскольку в математике существует следующее правило: запрещается делить на 0.

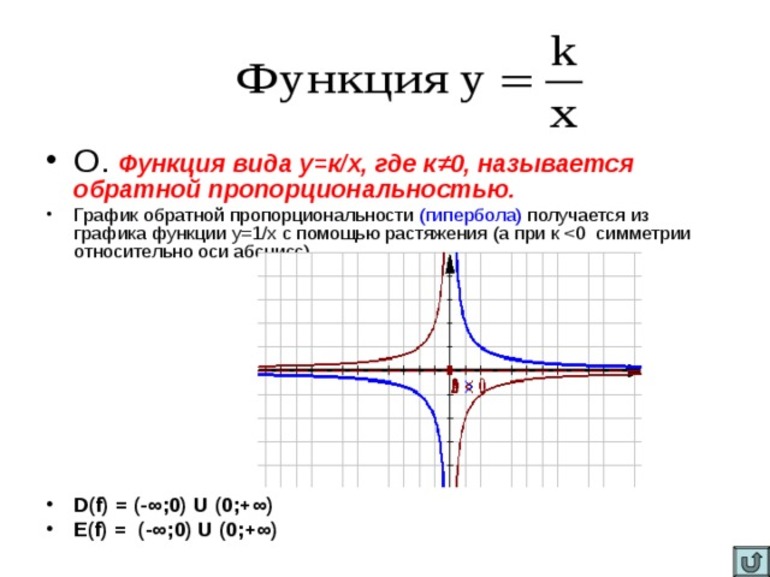
Следует отметить, что существует функция y = k/x и ее график — кривая, имеющая название гипербола. Многие путают его с параболой (в степени 2). Однако она является квадратичной. График строится в системе координат, которая называется декартовой. Кроме того, в математике встречается еще одно уравнение вида y = кх. Ее графиком является прямая.

Прямоугольная система координат

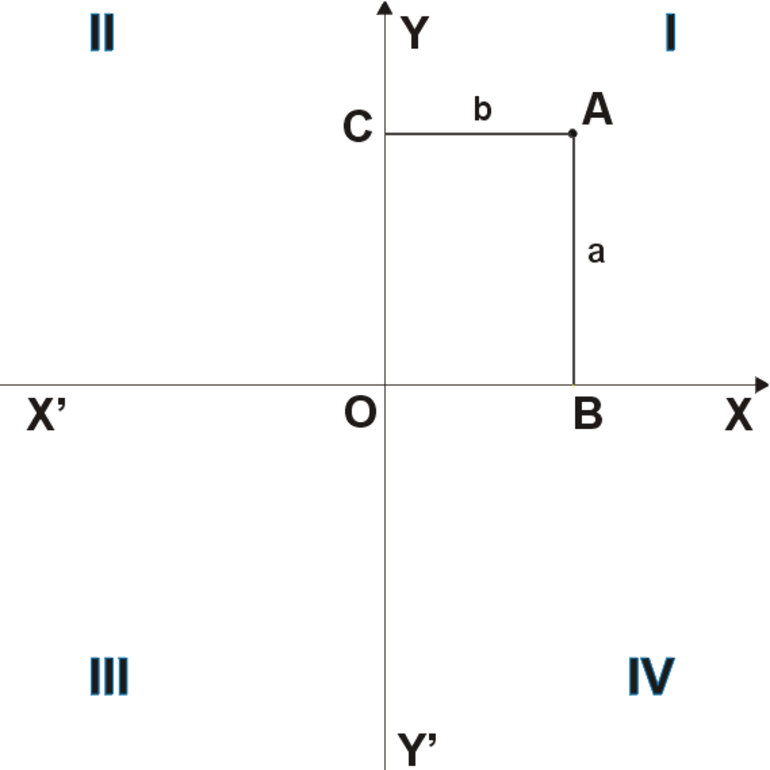
В математике существуют специальные инструменты для построения графиков функций. Одним из них считается распространенная прямоугольная система координат. Она может быть на плоскости и в пространстве. Поскольку y = k/x и y = kx являются элементарными, то для иллюстрации их графиков используется однородная прямоугольная декартовая система координат (рис. 1), элементом которой является точка.

Для декартовой системы на плоскости имеется только две координаты: по взаимно перпендикулярным осям ординат (ОУ) и абсцисс (ОХ). Они пересекаются в некоторой точке О, которая называется началом координат.

Рисунок 1. Прямоугольная декартова система координат (ДСК).

При указании координат нужно учитывать четверть. От нее зависит знак. Оси ординат (игрек) и абсцисс (икс) делят систему на четыре четверти. Они обозначаются римскими цифрами (рис. 1) и имеют такие свойства:

• Первая — I: координаты x и y являются положительными числами, т. е. x > 0 и y > 0.
• II: x 0.
• III: x 0 и y 0, то он является острым, т. е. его значение меньше 90 градусов. При к 0, то она располагается в I и III. Когда к 0 при х, принадлежащим промежутку (2;6) U [8;10]. Аналогично указывается отрезок, на котором заданная функция принимает отрицательные значения (f(x) 0). Следовательно, она обладает такими свойствами:

• График: кривая-гипербола.
• D(y) = (-inf;0) U (0;+inf).
• Если x > 0, то y > 0.
• При отрицательных величинах аргумента функция принимает отрицательные значения.
• Она убывает на интервалах: (-inf;0) и (0;+inf).
• Точек экстремума нет.
• Непрерывна, кроме точки х = 0.
• Непериодическая.
• Нечетная.

Когда к 0 при отрицательных значениях аргумента, а y 0. Функция y = kx обладает такими свойствами (k > 0):

Видео:🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

Уравнения с параметрами.

Исследование и решение уравнений с параметрами считается не самым простым разделом школьной математики. Однако, параметр, как понятие, часто воспринимается школьниками гораздо более сложным, чем есть в действительности. Здесь в первом пункте представлены очень простые вводные примеры использования параметров в уравнениях. Те, для кого это понятие не составляет большой трудности, могут сразу перейти к решению задач, которые представлены ниже.

Видео:Математика. 5 класс. Уравнение. Корень уравнения /15.09.2020/Скачать

Что такое уравнение с параметром?

Допустим нам нужно решить уравнение 2х + 5 = 2 − x.
Решение: 2x + x = 2 − 5; 3x = −3; x = −3/3 = −1.

Теперь нужно решить уравнение 2x + 5 = 3 − x.
Решение: 2x + x = 3 − 5; 3x = −2; x = −2/3

Затем нужно решить уравнение 2x + 5 = 0,5 − x.
Решение: 2x + x = 0,5 − 5; 3x = −4,5; x = −4,5/3 = −1,5.

А потом может потребоваться решить уравнение 2x + 5 = 10,7 − x или уравнение 2x + 5 = −0,19 − x.
Понятно, что уравнения похожи, а потому их решение будет сопровождаться теми же действиями, что выше. Возникает естественный вопрос — сколько можно делать одно и то же?

Уменьшим себе трудозатраты. Заметим, что все эти уравнения отличаются только одним числом в правой части. Обозначим это число символом a .
Получим уравнение 2х + 5 = a − х,
где a — переменная величина, вместо которой можно подставить нужное числовое значение и получить нужное уравнение. Эта переменная и называется параметром.

Решим это уравнение так же, как и все предыдущие.
Решение: 2х + 5 = a − x; 2x + x = a − 5; 3x = a − 5; x = (a − 5)/3.

Теперь для того, чтобы найти ответы для двух последних примеров, мы можем не повторять полностью всё решение каждого уравнения, а просто подставить в полученную формулу для х числовое значение параметра а:
x = (10,7 − 5)/3 = 5,7/3 = 1,9;
x = (−0,19 − 5)/3 = −5,19/3 = −1,73.

Таким образом, под термином «уравнение с параметром», фактически, скрывается целое семейство «почти одинаковых уравнений» , которые отличаются друг от друга только одним числом (одним слагаемым или одним коэффициентом) и одинаково решаются. Параметр — это число, которое меняется от уравнения к уравнению.
Полученную формулу для корня уравнения мы можем запрограммировать на компьютере. Достаточно будет только ввести значение параметра a, чтобы получить решение любого такого уравнения.

Рассмотрим еще один пример.

Замечаем, что они похожи друг на друга и отличаются только первым коэффициентом. Обозначим его, например, символом k.
Решим уравнение kх + 5 = 2 − x с параметром k.

С помощью этой формулы вычислим все ответы для приведенных уравнений.
x = −3/(2 + 1) = −1
x = −3/(3 + 1) = −0,75
x = −3/(−4 + 1) = 1
x = −3/(17 + 1) = −1/6

Можем ли мы теперь запрограммировать эту формулу и сказать, что с её помощью можно решить любое аналогичное уравнение?
Запрограммировать можем. Компьютер справится как с очень большими значениями коэффициента, так и с очень маленькими.
Например, если введём k = 945739721, то для уравнения заданного вида будет получен корень примерно равный −0,0000000031721201195353831188, если k = 0,0000004, то получим корень ≈ −2,9999988000004799998080000768.
Но, если мы введем в программу, казалось бы, более простое значение k = −1, то компьютер зависнет.
Почему?

Посмотрим внимательнее на формулу x = −3/(−1 + 1) = −3/0. Деление на ноль.
Посмотрим на соответствующее уравнение −1·х + 5 = 2 − x.
Преобразуем его −х + x = 2 − 5.
Оказывается, оно равносильно уравнению 0 = −3 (. ) и не может иметь корней.
Таким образом, из общего подхода к решению «почти одинаковых уравнений» могут существовать исключения, о которых нужно позаботиться отдельно. Т.е. провести предварительное исследование всего семейства уравнений. Именно этому и учатся на уроках математики с помощью так называемых задач с параметрами.

Видео:При каких отрицательных значениях k прямаяy = kx - 4 имеет с параболой ровно одну общую точку?Скачать

Графические способы решения уравнений

Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида f(x) = g(x) . Построим графики функций y = f(x) и y = g(x) и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.

Для быстрого построения эскизов графиков повторите еще раз графики элементарных функций, которые изучаются в школьном курсе математики, и правила преобразования графиков функций.

Рассмотрим примеры.

1. Решить уравнение
2х + 5 = 2 − x

Ответ: x = −1.

2. Решить уравнение
2х 2 + 4х − 1 = 2х + 3

3. Решить уравнение
log₂х = −0,5х + 4

Ответ: x = 2.

Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов — степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.

Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4 , а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже «от руки» разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:

1. Предварительный вывод: х ≈ 4.
2. Проверка: log₂4 = −0,5·4 + 4; 2 = −2 + 4; 2 ≡ 2.
3. Окончательный вывод х = 4.

Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Решение уравнений с параметрами с помощью графиков.

Задача 1.

Найти все значения параметра q при которых уравнение |x + 1| − |x − 3| − x = q 2 − 8q + 13 имеет ровно 2 корня.

При каждом значении параметра q можно вычислить значение выражения q 2 − 8q + 13 . Результат обозначим переменной а.
Т.е. примем q 2 − 8q + 13 = a и решим уравнение с параметром |x + 1| − |x − 3| − x = a

Строим график функции y = |x + 1| − |x − 3| − x , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.

Для каждого из этих участков раскроем модули с учётом знаков.
Вспомним: по определению |x| = x, если х ≥ 0, и |x| = −x, если х Чтобы проверить знаки модулей на участке достаточно подставить любое промежуточное значение x из этого отрезка, например, −2, 0 и 4.

Таким образом на участке I, где −∞ имеем −(x + 1) + (x − 3) − x = − x − 4.
Следовательно, должны построить график функции y = − x − 4 .
Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.

Аналогично, разбираемся с оставшимися двумя участками.

На участке II, где −1 имеем (x + 1) + (x − 3) − x = x − 2
и должны построить соответствующую часть графика функции y = x − 2 .

На участке III, где 3 , имеем (x + 1) − (x − 3) − x = − x + 4
и должны построить соответствующую часть графика функции y = − x + 4 .

Последовательное построение итогового графика показано ниже. (Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.)

Замечание: если вы освоили тему Преобразование графиков функций, то с этой частью задачи сможете справиться быстрее, чем показано в примере.

Итак, построение графика функции, расположенной в левой части уравнения, мы завершили. Посмотрим, что находится в правой части.

График функции y = a представляет собой прямую линию, параллельную оси абсцисс (Ox), и пересекающую ось ординат (Oy) в точке а. Так как а — параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.

Из рисунка видно, что количество точек пересечения каждой из красных прямых с ранее построенным (зелёным) графиком зависит от высоты, на которой расположена эта прямая, т.е. от параметра а. Прямые, расположенные ниже y = −3 , пересекают график в одной точке, а значит эти уравнения имеют только одно решение. Прямые, проходящие на уровне −3 имеют по три точки пересечения, значит соответствующие уравнения будут иметь по три решения. Прямые, расположенные выше точки y = 1 , снова имеют только по одной точке пересечения.
Ровно две точки пересечения с зелёным графиком будут иметь только прямые y = 1 и y = −3 . Соответствующие уравнения будут иметь ровно два корня, что и требовалось определить в задании.

Однако мы нашли значения введённого нами параметра а, при котором заданное уравнение имеет 2 корня, а вопрос задачи состоял в том, чтобы найти все значения параметра q. Для этого придётся решить следующую совокупность уравнений:

Это обычные квадратные уравнения, которые решаются через дискриминант или по теореме Виета.

Таким образом, окончательный ответ: .

Задача 2.

Найти все значения параметра a, при которых уравнение (2 − x)x(x − 4) = a имеет ровно 3 корня.

Рассмотрим функцию y = (2 − x)x(x − 4) . Видно, что если раскрыть скобки, то старший член будет −х 3 . Т.е. графиком функции должна быть кубическая парабола, причем на при x, стремящемcя к +∞, y → −∞, а при x, стремящемся к −∞, y → +∞.
Поскольку уравнение (2 − x)x(x − 4) = 0 имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с «волной». Строим от руки эскиз графика.

Правая часть уравнения y = a такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.

Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения y_max и y_min через производную. (Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют.

Ответ:

Видео:ЕГЭ по математике. Профильный уровень. Задание 5. Найдите корень уравненияСкачать

Задача для самостоятельного решения

Задача 3.

При каком наибольшем отрицательном значении параметра а уравнение имеет один корень?

Ответ: -1,625

Задача реального экзамена ЗНО-2013 (http://www.osvita.ua/).

Переход на главную страницу сайта «Математичка».

Есть вопросы? пожелания? замечания?
Обращайтесь — mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Функция y=k/х свойства и график, область определения функции, коэффициент в графике функции, примеры решения задач

Во время решения задач по математике учащиеся сталкиваются с функцией у = к/х, которую нужно не только обследовать, но и построить ее график. Очень часто новички делают много ошибок, поскольку считают, что только прямая имеет такое уравнение. Для получения знаний в исследовании следует ознакомиться подробно со свойствами и формулами.

Видео:При каких отрицательных значениях k прямая y=kx-4 имеет с параболой y=x^2+2x одну общую точкуСкачать

Общие сведения

Функцией называется некоторая зависимость переменных друг от друга. В некоторых случаях неизвестные величины могут быть выражены системой конкретных значений, интервалами, а также другими функциональными выражениями. Последний класс называется сложным или составным. Различают зависимые и независимые переменные (аргументы). Второй тип может принимать любые значения, кроме тех, которые превращают выражение в неопределенность.

Однако аргументы необходимо также обследовать, поскольку они могут обратить тождество в пустое множество. Одним из таких примеров является функция у = к / х. Ее аргумент x может принимать любые значения, кроме 0. Именно это число превращает уравнение в неопределенность, поскольку в математике существует следующее правило: запрещается делить на 0.

Следует отметить, что существует функция y = k/x и ее график — кривая, имеющая название гипербола. Многие путают его с параболой (в степени 2). Однако она является квадратичной. График строится в системе координат, которая называется декартовой. Кроме того, в математике встречается еще одно уравнение вида y = кх. Ее графиком является прямая.

Прямоугольная система координат

В математике существуют специальные инструменты для построения графиков функций. Одним из них считается распространенная прямоугольная система координат. Она может быть на плоскости и в пространстве. Поскольку y = k/x и y = kx являются элементарными, то для иллюстрации их графиков используется однородная прямоугольная декартовая система координат (рис. 1), элементом которой является точка.

Для декартовой системы на плоскости имеется только две координаты: по взаимно перпендикулярным осям ординат (ОУ) и абсцисс (ОХ). Они пересекаются в некоторой точке О, которая называется началом координат.

Рисунок 1. Прямоугольная декартова система координат (ДСК).

При указании координат нужно учитывать четверть. От нее зависит знак. Оси ординат (игрек) и абсцисс (икс) делят систему на четыре четверти. Они обозначаются римскими цифрами (рис. 1) и имеют такие свойства:

• Первая — I: координаты x и y являются положительными числами, т. е. x > 0 и y > 0.
• II: x 0.
• III: x 0 и y Коэффициент пропорциональности

В математических дисциплинах бывает два типа пропорциональности — прямая и обратная. Они применяются для описания различных процессов, исследования дифференциальных уравнений, физических величин и законов.

Прямой пропорциональностью называется некоторая линейная функция вида y = kx, в которой аргументом является х, а к — коэффициент прямой пропорциональности. Иными словами, произведение к на аргумент x есть величина, определяющая прямую пропорциональную зависимость одной величины от другой. Обратной пропорциональностью называется некоторая функция вида y = k/x, значение аргумента которой никогда не равно нулю.

Графиком линейной функции вида y = kx является прямая, проходящая через начало координат в точке О(0;0). От к зависит угол наклона прямой. Если к > 0, то он является острым, т. е. его значение меньше 90 градусов. При к 0, то она располагается в I и III. Когда к Исследование функции

Для полного анализа поведения функции применяется методика или алгоритм ее исследования. Это нужно прежде всего для подробного графика. Однако перед началом выполнения этой операции следует ознакомиться с основными пунктами полного исследования заданной функции. К ним относятся следующие:

• Область определения — D(f).
• Область допустимых значений — E(f).
• Нули.
• Знаковые промежутки.
• Периодичность.
• Параметры четности.
• Экстремумы (MAX и MIN).
• Монотонность (интервалы).

Однако некоторые пункты можно опускать или менять местами. После этого необходимо строить график, учитывая все необходимые материалы исследования. Следует подробно разобрать каждый пункт, поскольку только верное решение дает возможность построить правильный график. Кроме того, специалисты рекомендуют освоить интервалы и их правильную запись.

Правила записи интервалов

В некоторых пунктах алгоритма исследования функции встречается термин «промежуток» или «интервал». От правильности его задания зависит решение задачи. Во всем мире приняты обозначения, которые помогут сделать запись понятной и грамотной:

• Обозначение жесткой границы (включительно) квадратными скобками [], а значения, не входящего в интервал (не включительно), — круглыми скобками ().
• Тип границ можно комбинировать.
• Для объединения промежутков применяется специальный символ U.
• Бесконечность можно обозначать символом или inf. Например, (-inf;inf).
• Перед и после бесконечности всегда ставится круглая скобка.
• Порядок комбинации промежутков (интервалов или числовых отрезков): последовательно от большего к меньшему. Например, (-inf;-8) U (-4;0] U [5;8] U (10;15).

Обозначение inf используется в некоторых языках программирования или математических пакетах. В дисциплине «Алгебра и начало анализа» интервалы встречаются очень часто, поскольку она основана на исследовании выражений, уравнений, неравенств, функций и т. д. После ознакомления с правилами записи промежутков следует переходить к первому пункту — нахождению D(f).

Область определения и допустимые значения

Все значения аргумента, при которых существует заданная функция вида z = f(y), называется областью ее определения. Обозначается параметр комбинацией букв D(имя функции), т. е. D(z) или D(f(y)). Величина D(z) зависит от типа функции, в том числе от ее сложности. Если она состоит из нескольких простых элементов, то нужно рассматривать D(z) для каждого из них. Параметр всегда записывается в виде промежутка, на котором существует зависимая переменная.

Областью допустимых значений функции z = f(y) являются все значения, при которых она существует. Обозначается величина литерой Е(имя функции). Например, запись для z = f(y) выглядит таким образом: Е(z) или Е(f(y)). Этот параметр тоже зависит от типа выражения, как и D(z). Задается в виде интервала. Для его задания необходимо выяснить, при каких значениях функция не существует. Например, для z = 2 / y. В искомом выражении у не может быть равен 0. Следовательно, у принадлежит следующему интервалу: (-inf;0) U (0;inf). Для z = 3y параметр Е(z) = (-inf;inf), поскольку при любых значениях функция существует.

Нули и знаковые промежутки

Нулями функции называются все значения независимой переменной, при которых ее график пересекается с осями ОУ и ОХ. Для нахождения точки пересечения с ОУ необходимо подставить х = 0 в выражение и выполнить расчеты. Чтобы найти пересечение или пересечения с осью иксов, нужно решить уравнение, приравняв его к 0.

Знаковые промежутки (интервал знакопостоянства) — отрезки, на которых функция меняет знак на противоположный. Если интервал положительный, то короткая запись выглядит таким образом: f(x) > 0 при х, принадлежащим промежутку (2;6) U [8;10]. Аналогично указывается отрезок, на котором заданная функция принимает отрицательные значения (f(x) Периодичность и четность

Периодической является функция, повторяющая значения через некоторый период Т (регулярный интервал). Ее значения не меняются при добавлении к аргументу некоторого числа, неравного нулевому значению. Математическая запись для z = f(y) имеет такой вид: z = f(y + T) = f(y — T). Для любой периодической функции справедливо также следующее равенство: z = f(y + nT). Коэффициент n — любое целочисленной значение.

Для выявления признака четности следует воспользоваться очень простым соотношением f(y) = f(-y). Для этого необходимо подставить в выражение положительное, а затем отрицательное значение аргумента. Если в первом и втором случаях равенство будет выполняться, то можно сделать вывод о четности. Когда соотношение не выполняется, тогда исходная функция является нечетной.

Монотонность и экстремумы

Монотонная — функция z = f(x), которая может только возрастать или убывать (понижение) на всей области определения. Для исследования нужно воспользоваться следующим алгоритмом:

• Найти первую производную.
• Определить критические точки, приравняв производную к 0.
• Выяснить знаки производной на промежутках.
• Сделать выводы.

Далее нужно определить экстремумы, т. е. минимальное и максимальное значения функции на всей области ее определения. В этом случае также существуют определенные правила:

• Найти D(z) и сравнить его с отрезком, на котором нужно найти экстремумы (должен принадлежать D(z)).
• Найти производную заданной функции.
• Выполнить поиск стационарных точек (производная приравнивается к 0 и решается уравнение).
• Подставить корни уравнения в исходную функцию.
• Найти минимальное и максимальное значения.

Следует учесть все точки. Однако перед выполнением 4 пункта следует отсеять ложные корни. Для этого следует подставить в уравнение корни. Они должны соответствовать равенству. Если этого не происходит, то корень отсеивается.

Видео:🔴 Найдите корень уравнения 2(3-2x)-7=-3x+8 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

Информация о свойствах

В некоторых источниках описываются свойства y = k/x и ее график. Следует отметить, что они получаются при исследовании последней. Существует два состояния. При первом коэффициент пропорциональности больше 0 (k > 0). Следовательно, она обладает такими свойствами:

• График: кривая-гипербола.
• D(y) = (-inf;0) U (0;+inf).
• Если x > 0, то y > 0.
• При отрицательных величинах аргумента функция принимает отрицательные значения.
• Она убывает на интервалах: (-inf;0) и (0;+inf).
• Точек экстремума нет.
• Непрерывна, кроме точки х = 0.
• Непериодическая.
• Нечетная.

Когда к 0 при отрицательных значениях аргумента, а y 0. Функция y = kx обладает такими свойствами (k > 0):

• График: прямая.
• D(y) = (-inf;+inf).
• Если x > 0, то y > 0. Когда x 0 при x Пример решения

Существует некоторый тип задач, в которых нужно исследовать и построить график функции y = k/x. Разобрать решение можно на примере y = 5 / (x — 3). Следует воспользоваться алгоритмом:

• D(5 / (x — 3)) = (-inf;3) U (3;+inf).
• Нули функции. По ОУ: y = 5 / (0 — 3) = — 5/3. По ОХ: 5 / (x — 3) = 0. Если решить уравнения, то у него нет корней.
• Знаковые промежутки: (-inf;3) и (3;+inf).
• Непериодическая.
• Четность: 5 / (-x — 3) = — 5 / (x + 3). Нечетная: — 5 / (x + 3) не равно 5 / (x — 3).
• Экстремумы: y’ = [5 / (x — 3)] = — 5 / (x — 3)^2 = 0. Уравнение не имеет решений, а это значит, что максимума и минимума нет.
• Не является монотонной.

Чтобы построить график функции y = k / x + 3 (к = 5), нужно составить таблицу для его построения.

Таблица 1. Зависимость значения функции от ее аргумента.

После составления таблицы нужно начертить ДСК. На ней следует отмечать точки, а затем их плавно соединить (рис. 2).

Рисунок 2. График обратной пропорциональности y = k / x — 3 при к = 5.

Математики рекомендуют для проверки применять специализированные веб-приложения. Одним из них является онлайн-сервис, который называется yotx.

Таким образом, графиком обратной пропорциональности является гипербола, а прямой пропорциональности — прямая. Поведение функции исследуется по специальному алгоритму, который позволяет легко построить ее график и выяснить некоторые свойства.

📹 Видео

ЕГЭ 2015 База 7.3 : Найдите отрицательный корень уравнения x^2-x-6=0 #7Скачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Найдите корень уравнения 2^(4-2x) = 64Скачать

🔴 Найдите корень уравнения (x-8)^2=(x-2)^2 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

🔴 Найдите корень уравнения (1/7)^(x-5)=49 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Уравнение. 5 класс.Скачать

Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать

Математика. 5 класс. Уравнение. Корень уравнения /16.09.2020/Скачать