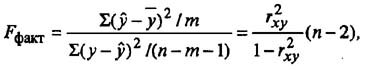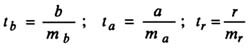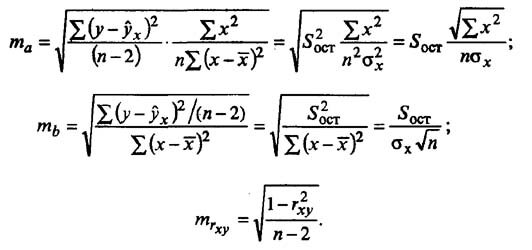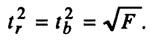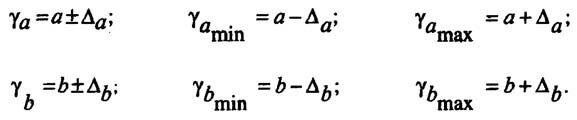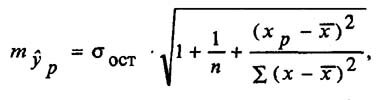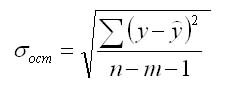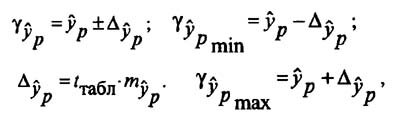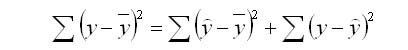Использование критерия Стьюдента для проверки значимости параметров регрессионной модели

Проверка статистической значимости параметров регрессионного уравнения (коэффициентов регрессии) выполняется по t-критерию Стьюдента, который рассчитывается по формуле:

где P — значение параметра;
S_p — стандартное отклонение параметра.

Рассчитанное значение критерия Стьюдента сравнивают с его табличным значением при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы N—k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели Y=A*X+B подставляем k=1).

Если вычисленное значение t_p выше, чем табличное, то коэффициент регрессии является значимым с данной доверительной вероятностью. В противном случае есть основания для исключения соответствующей переменной из регрессионной модели.

Величины параметров и их стандартные отклонения обычно рассчитываются в алгоритмах, реализующих метод наименьших квадратов.

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Проверка значимости модели множественной регрессии и ее параметров

Для оценки значимости параметров уравнения множественной регрессии используют критерий Стьюдента. Напомним, что значимость параметров означает их отличие от нуля с высокой долей вероятности. Нулевой гипотезой в данном случае является утверждение

Фактическое значение t-критерия определяется по формуле

(2.27)

В формуле (2.27) под оценкой параметра понимается как коэффициент регрессии, так и свободный член (при ). Величина среднего квадратического отклонения оцениваемого параметра определяется как корень из дисперсии , рассчитанной по формуле (2.25). Величину называют стандартной ошибкой параметра .

Формулу для оценки коэффициента регрессии (т.е. для ) можно привести к виду

(2.28)

где – среднее квадратическое отклонение результативной переменной ; – среднее квадратическое отклонение объясняющей переменной , являющейся сомножителем коэффициента ; – коэффициент детерминации, найденный для уравнения зависимости переменной от переменных , включая ; – коэффициент детерминации, найденный для уравнения зависимости переменной от других переменных , входящих в рассматриваемую модель множественной регрессии.

Теоретическое значение t-критерия находят по таблице значений критерия Стьюдента для уровня значимости а и числа степеней свободы . Уровень значимости а представляет собой вероятность ошибки первого рода, т.е. вероятность отвергнуть гипотезу , когда она верна. Как правило, а выбирают равным 0,1; 0,05 или 0,01.

Нулевая гипотеза о незначимости параметра : отвергается, если выполняется неравенство

(2.29)

где – теоретическое значение критерия Стьюдента.

На основе выражения (2.29) можно построить также доверительный интервал для оцениваемого параметра :

(2.30)

Выражение (2.30) позволяет как оценить значимость параметра, так и дать его экономическую интерпретацию (если оценивается коэффициент регрессии). Очевидно, что параметр будет значим, если в доверительный интервал (2.30) не входит нуль, т.е. с большой долей вероятности оцениваемый параметр не равен нулю.

Так как коэффициент регрессии является абсолютным показателем силы связи, границы доверительного интервала и для него также можно интерпретировать аналогичным образом: с вероятностью при единичном изменении независимой переменной зависимая переменная у изменится не меньше, чем на , и не больше, чем на .

Рассмотрим результаты оценки значимости параметров для примера 2.1. Стандартные ошибки параметров равны

Напомним, что под знаком корня в квадратных скобках стоит элемент матрицы , который находится на пересече-

нии j-й строки и j-го столбца, номер; равен номеру оцениваемого параметра.

Фактическое значение критерия Стьюдента равно

Табличное значение t-критерия для и уровне значимостисоставляет 2,0153, следовательно, все параметры, кроме свободного члена, значимы .

Найдем границы доверительных интервалов для коэффициентов регрессии.

Отметим, что, руководствуясь значениями границ доверительных интервалов, можно сделать те же выводы о значимости коэффициентов регрессии (так как нуль не попадает в доверительный интервал). Выводы в данном случае и не могли быть иными, чем при сравнении фактического и табличного значений критерия Стьюдента, так как формула (2.30) является следствием формулы (2.29). Дадим экономическую интерпретацию границ доверительных интервалов для коэффициентов регрессии.

Коэффициент является характеристикой силы связи между объемом поступления налогов и количеством занятых. С учетом значений границ доверительного интервала дляможно сказать, что изменение количества занятых на 1 тыс. человек приведет к изменению (с вероятностью 0,95 ()) поступления налогов не менее чем на 3,56 млн руб. и не более чем на 21,34 млн руб. при неизменном объеме отгрузки в обрабатывающих производствах и производстве энергии. Для двух других коэффициентов регрессии выводы будут следующими.

Изменение объема отгрузки в обрабатывающих производствах на 1 млн руб. приведет к изменению (с вероятностью 0,95 ()) поступления налогов не менее чем на 0,028 млн руб. и не более чем на 0,092 млн руб. при неизменных значениях количества занятых и производства энергии.

При изменении производства энергии на 1 млн руб. поступление налогов изменится (с вероятностью 0,95 ()) не менее чем на 0,13 млн руб. и не более чем на 0,18 млн руб. при неизменных значениях количества занятых и объема отгрузки в обрабатывающих производствах.

Как было отмечено в параграфе 2.2, при построении модели регрессии с использованием центрированных переменных коэффициенты регрессии не отличаются от коэффициентов регрессии в натуральной форме. Это утверждение относится также к величине стандартных ошибок коэффициентов регрессии и, следовательно, к фактическим значениям критерия Стьюдента.

При использовании стандартизованных переменных меняется масштаб их измерения, что приводит к другим, чем в исходной регрессии, значениям параметров (стандартизованных коэффициентов регрессии) и их стандартных ошибок. Однако фактические значения критерия Стьюдента для параметров уравнения в стандартизованном масштабе совпадают с теми значениями, которые были получены по уравнению в натуральном масштабе.

Для оценки значимости всего уравнения регрессии в целом используется критерий Фишера (F-критерий), который в данном случае называют также общим F-критерием. Под незначимостью уравнения регрессии понимается одновременное равенство нулю (с высокой долей вероятности) всех коэффициентов регрессии в генеральной совокупности:

Фактическое значение F-критерия определяется как соотношение факторной и остаточной сумм квадратов, рассчитанных по уравнению регрессии и скорректированных на число степеней свободы:

(2.31)

где – факторная сумма квадратов; – остаточная сумма квадратов.

Теоретическое значение F-критерия находят по таблице значений критерия Фишера для уровня значимости α, числа степеней свободы и . Нулевая гипотеза отвергается, если

где – теоретическое значение критерия Фишера.

Отметим, что если модель незначима, то незначимы и показатели корреляции, рассчитанные по ней. Действительно, если

то

и линия регрессии параллельна оси абсцисс. Кроме того, из системы нормальных уравнений, полученной по методу наименьших квадратов (2.8), следует, что .

При нулевых значения всех коэффициентов регрессии имеем выражение

т.е. при равенстве всех коэффициентов регрессии нулю (их статистической незначимости) коэффициент детерминации также будет равен нулю (статистически незначим).

Формулу (2.31) расчета F-критерия можно преобразовать, разделив факторную и остаточную суммы квадратов на общую сумму квадратов:

После простых преобразований получаем выражение

Расчет общего F-критерия можно оформить в виде таблицы дисперсионного анализа (табл. 2.2).

Таблица 2.2. Анализ статистической значимости модели множественной регрессии

Число степеней свободы df

Сумма квадратов SS

Дисперсия на одну степень свободы MS = SS/df

табличное значение для а = 0,05

Аналогичную таблицу дисперсионного анализа можно увидеть в результатах компьютерной обработки данных. Ее отличие

от приведенной выше таблицы заключается в содержании последнего столбца. В нашем случае это теоретическое значение критерия Фишера. В компьютерных вариантах в последнем столбце приводится значение вероятности допустить ошибку первого рода (отвергнуть верную нулевую гипотезу), которая соответствует фактическому значению F-критерия. В Excel эта величина называется «значимость F». Обозначим величину, выдаваемую компьютером в таблице дисперсионного анализа, как . Ее значение можно проинтерпретировать следующим образом: если теоретическое значение F-критерия равно его фактическому значению, то вероятность ошибки первого рода (уровень значимости) равна .

Выбирая для определения табличного значения критерия некий уровень значимости, мы соглашаемся на величину ошибки, равную. Следовательно, если , то фактическая ошибка будет меньше запланированной и можно говорить о значимости уравнения регрессии при заданном уровне значимости .

Проверим на статистическую значимость уравнение регрессии, полученное в примере 2.1. Фактическое значение F-критерия равно

Табличное значение критерия Фишера для а = 0,05, числа степеней свободы и равно 2,82. Так как фактическое значение F-критерия больше табличного, уравнение регрессии значимо с вероятностью Следовательно, значим также коэффициент детерминации, т.е. он с большой долей вероятности отличен от нуля.

При использовании опции «Регрессия» в ППП Excel для данного примера получена следующая таблица дисперсионного анализа (табл. 2.3).

Таблица 2.3. Таблица дисперсионного анализа, полученная при применении опции «Регрессия» в ППП Excel

Видео:Т-критерий Стьюдента за 12 минут. Биостатистика.Скачать

Критерий Фишера и критерий Стьюдента в эконометрике

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где n — число наблюдений;
m — число параметров при факторе х.

F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Таблицы по нахождению критерия Фишера и Стьюдента

Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.

Табличное значение критерия Фишера вычисляют следующим образом:

1. Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
2. Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
3. На пересечении столбца k1 и строки k2 находят значение критерия Фишера

Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).

Видео:Критерий Фишера для проверки адекватности построенной регрессииСкачать

Критерии Стьюдента

Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.

Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.

Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт

Видео:Коварный t критерий СтьюдентаСкачать

Видео лекциий по расчету критериев Фишера и Стьюдента

Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео

Лекция 1. Критерии и Гипотезы

Лекция 2. Критерии и Гипотезы

Лекция 3. Критерии и Гипотезы

Видео:t критерий Стьюдента для независимых выборокСкачать

Определение доверительных интервалов

Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:

Формулы для нахождения доверительных интервалов выглядят так

Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза

и находится доверительный интервал

Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:

общая сумма квадратов отклонений (TSS)

сумма квадратов отклонений, обусловленная регрессией (RSS)

остаточная сумма квадратов отклонений (ESS)

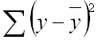
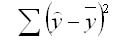
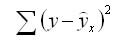
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.

🌟 Видео

t-критерий Стьюдента для проверки гипотезы о средней в MS ExcelСкачать

Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

расчет t-критерия СтьюдентаСкачать

Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

Эконометрика. Линейная парная регрессияСкачать

10-02 Критерий знаковСкачать

T-критерий СТЬЮДЕНТА | АНАЛИЗ ДАННЫХ #7Скачать

2.7. Распределение Хи квадрат, Стьюдента, Фишера .Скачать

Сравнение двух средних; t-критерий СтьюдентаСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

Коэффициент корреляции. Статистическая значимостьСкачать

Статистический метод (критерий): как выбрать для анализа?Скачать

Хи-квадрат Пирсона: когда выбирать и как использоватьСкачать

Т критерий стьюдента для зависимых данныхСкачать