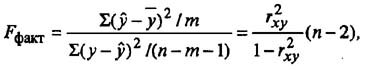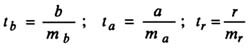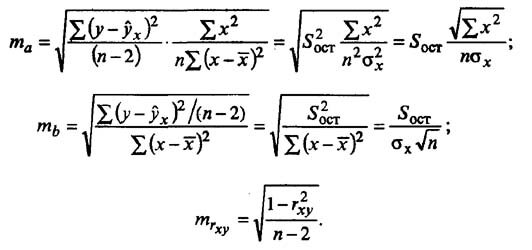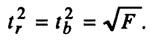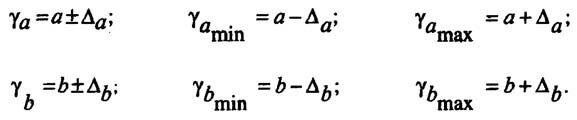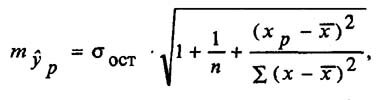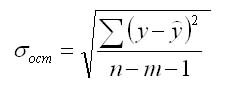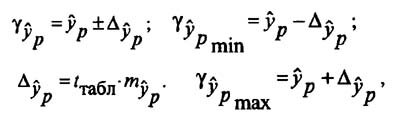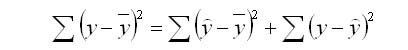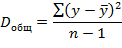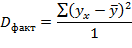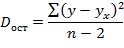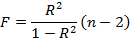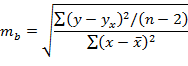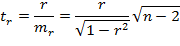Содержание

Использование критерия Стьюдента для проверки значимости параметров регрессионной модели
Критерий Фишера и критерий Стьюдента в эконометрике
Таблицы по нахождению критерия Фишера и Стьюдента
Критерии Стьюдента
Видео лекциий по расчету критериев Фишера и Стьюдента
Определение доверительных интервалов
Оценка значимости по критериям Фишера и Стьюдента
📺 Видео

Использование критерия Стьюдента для проверки значимости параметров регрессионной модели

Проверка статистической значимости параметров регрессионного уравнения (коэффициентов регрессии) выполняется по t-критерию Стьюдента, который рассчитывается по формуле:

где P — значение параметра;
S_p — стандартное отклонение параметра.

Рассчитанное значение критерия Стьюдента сравнивают с его табличным значением при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы N—k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели Y=A*X+B подставляем k=1).

Если вычисленное значение t_p выше, чем табличное, то коэффициент регрессии является значимым с данной доверительной вероятностью. В противном случае есть основания для исключения соответствующей переменной из регрессионной модели.

Величины параметров и их стандартные отклонения обычно рассчитываются в алгоритмах, реализующих метод наименьших квадратов.

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Критерий Фишера и критерий Стьюдента в эконометрике

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где n — число наблюдений;
m — число параметров при факторе х.

F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Видео:Т-критерий Стьюдента за 12 минут. Биостатистика.Скачать

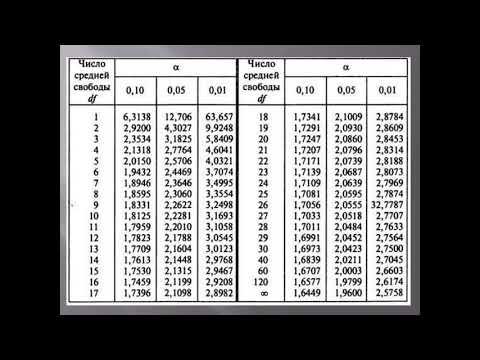
Таблицы по нахождению критерия Фишера и Стьюдента

Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.

Табличное значение критерия Фишера вычисляют следующим образом:

Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
На пересечении столбца k1 и строки k2 находят значение критерия Фишера

Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Критерии Стьюдента

Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.

Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.

Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт

Видео:Коварный t критерий СтьюдентаСкачать

Видео лекциий по расчету критериев Фишера и Стьюдента

Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео

Лекция 1. Критерии и Гипотезы

Лекция 2. Критерии и Гипотезы

Лекция 3. Критерии и Гипотезы

Видео:Критерий Фишера для проверки адекватности построенной регрессииСкачать

Определение доверительных интервалов

Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:

Формулы для нахождения доверительных интервалов выглядят так

Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза

и находится доверительный интервал

Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:

общая сумма квадратов отклонений (TSS)

сумма квадратов отклонений, обусловленная регрессией (RSS)

остаточная сумма квадратов отклонений (ESS)

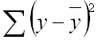
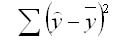
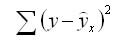
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.

Видео:Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Оценка значимости по критериям Фишера и Стьюдента

После выбора уравнения линейной регрессии и оценки его параметров проводится оценка статистической значимости как уравнения в целом, так и отдельных его параметров.

Оценка значимости уравнения регрессии в целом осуществляется с помощью критерия Фишера, который называют также F-критерием. При этом выдвигается нулевая гипотеза (Н₀): коэффициент регрессии равен нулю (b = 0), следовательно, фактор х не оказывает влияния на результат у и линия регрессии параллельна оси абсцисс.

Перед тем как приступить к расчету критерия Фишера, проведем анализ дисперсии. Общую сумму квадратов отклонений у от можно разложить на сумму квадратов отклонений, объясненную регрессией и сумму квадратов отклонений, не объясненную регрессией:

где Σ(y — ) 2 — общая сумма квадратов отклонений значений результата от среднего по выборке; Σ(y_x — ) 2 — сумма квадратов отклонений, объясненная регрессией; Σ(y — у_х) 2 — сумма квадратов отклонений, не объясненная регрессией, или остаточная сумма квадратов отклонений.

Общая сумма квадратов отклонений результативного признака у от среднего значения определяется влиянием различных причин. Условно всю совокупность причин можно разделить на две группы: изучаемый фактор х и прочие, случайные и не включаемые в модель факторы. Если фактор х не оказывает влияния на результат, то линия регрессии на графике параллельна оси абсцисс и = y_х. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадает с остаточной:

Σ(y — ) 2 = Σ(y — у_х) 2 ,

Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов:

Σ(y — ) 2 = Σ(y_x — ) 2

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс, обусловленный как влиянием фактора х, (регрессией у по х), так и действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат у. Это равносильно тому, что коэффициент детерминации R 2 будет приближаться к единице.

Любая сумма квадратов отклонений связана с числом степеней свободы df, т.е. с числом свободы независимого варьирования признака.

Для общей суммы квадратов Σ(y — ) 2 требуется (п-1) независимых отклонений, ибо в совокупности из п единиц после расчета среднего уровня свободно варьируют лишь (п-1) число отклонений.

При заданном наборе переменных у и х расчетное значение у_х является в линейной регрессии функцией только одного параметра — коэффициента регрессии b. Таким образом, факторная сумма квадратов отклонений имеет число степеней свободы, равное единице. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет (п-2).

Существует равенство между числами степеней свободы общей, факторной и остаточной сумм квадратов.Запишем два равенства:

Σ(y — ) 2 = Σ(y_x — ) 2 + Σ(y — у_х) 2 ,

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим дисперсии на одну степень свободы:

Так как эти дисперсии рассчитаны на одну степень свободы, их можно сравнивать между собой. Критерий Фишера позволяет проверить нулевую гипотезу Н₀ о том, что факторная и остаточная дисперсии на одну степень свободы равны между собой (D_факт=D_ост). Критерий Фишера рассчитывается по следующей формуле:

Если гипотеза Н₀ подтверждается, то факторная и остаточная дисперсии одинаковы, и уравнение регрессии незначимо. Чтобы отвергнуть нулевую гипотезу и подтвердить значимость уравнения регрессии в целом, факторная дисперсия на одну степень свободы должна превышать остаточную дисперсию на одну степень свободы в несколько раз. Существуют специальные таблицы критических значений Фишера при различных уровнях надежности и степенях свободы. В них содержатся максимальные значения отношений дисперсий, при которых нулевая гипотеза подтверждается. Значение критерия Фишера для конкретного случая сравнивается с табличным, и на основе этого гипотеза Н₀ принимается или отвергается.

Если F_факт > F_табл , тогда гипотеза Н₀ отклоняется и делается вывод, что связь между у и х существенна и уравнение регрессии статистически значимо. Если F_факт ≤ F_табл , тогда гипотеза Н₀ принимается и делается вывод, что уравнение регрессии статистически незначимо, так как существует риск (при заданном уровне надежности) сделать неправильный вывод о наличии связи между х и у.

Между критерием Фишера и коэффициентом детерминации существует связь, которая выражается следующей формулой для парной линейной регрессии:

В линейной регрессии часто оценивается не только значимость уравнения регрессии в целом, но и значимость его отдельных параметров, а также коэффициента корреляции.

Для того чтобы осуществить такую оценку, необходимо для всехпараметров рассчитывать стандартные ошибки (т_а , т_b , т_r):

Теперь нужно рассчитать критерии Стьюдента t_a, t_b, t_r·. Для параметров а, b и коэффициента корреляции r критерий Стьюдента определяет соотношение между самим параметром и его ошибкой:

Фактические значения критерия Стьюдента сравниваются с табличными при определенном уровне надежности α и числе степеней свободы df= (п-2). По результатам этого сравнения принимаются или отвергаются нулевые гипотезы о несущественности параметров или коэффициента корреляции. Если фактическое значение критерия Стьюдента по модулю больше табличного, тогда гипотеза о несущественности отвергается. Подтверждение существенности коэффициента регрессии равнозначно подтверждению существенности уравнения регрессии в целом.

В парной линейной регрессии между критерием Фишера, критериями Стьюдента коэффициентов регрессии и корреляции существует связь.

На основании полученной связи можно сделать вывод, что статистическая незначимость коэффициента регрессии или коэффициента корреляции влечет за собой незначимость уравнения регрессии в целом, либо, наоборот, незначимость уравнения регрессии подразумевает несущественность указанных коэффициентов.

На основе стандартных ошибок параметров и табличных значений критерия Стьюдента можно рассчитать доверительные интервалы:

Поскольку коэффициент регрессии имеет четкую экономическую интерпретацию, то доверительные границы интервала для него не должны содержать противоречивых результатов. Например, такая запись, как -5≤ b ≤ 10, указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже нуль, а этого не может быть. Следовательно, связь между данными нельзя выразить такой моделью (в частности, парной линейной регрессией), должна подбираться другая модель.

Дата добавления: 2015-10-05 ; просмотров: 13649 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ