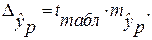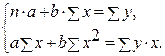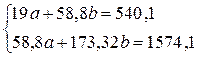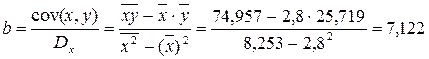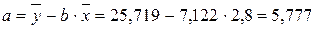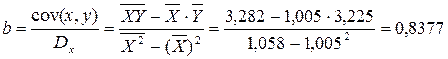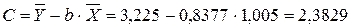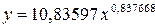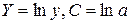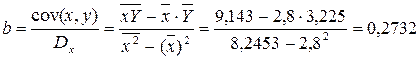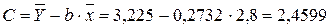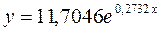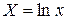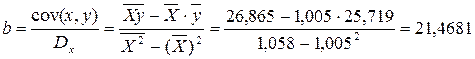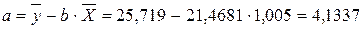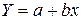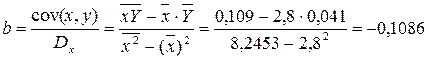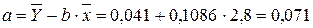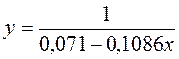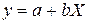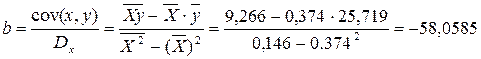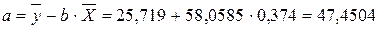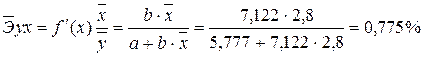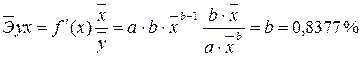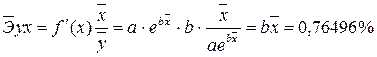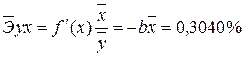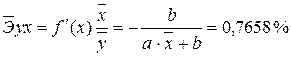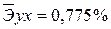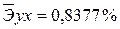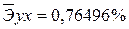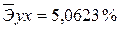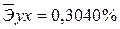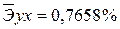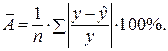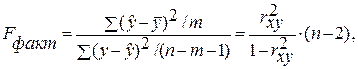Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
- Понятие линейной регрессии. Парная линейная регрессия
- Уравнение парной линейной регрессии и метод наименьших квадратов
- Определение коэффициентов уравнения парной линейной регрессии
- Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение
- Анализ качества модели линейной регрессии
- Коэффициент детерминации
- F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
- Сумма квадратов остатков
- Стандартная ошибка регрессии
- Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной
- Задачи регрессионного анализа
- Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии
- Контрольная работа: Парная регрессия
- Основы линейной регрессии
- Что такое регрессия?
- Линия регрессии
- Метод наименьших квадратов
- Предположения линейной регрессии
- Аномальные значения (выбросы) и точки влияния
- Гипотеза линейной регрессии
- Оценка качества линейной регрессии: коэффициент детерминации R 2
- Применение линии регрессии для прогноза
- Простые регрессионные планы
- Пример: простой регрессионный анализ
- Задача исследования
- Просмотр результатов
- Коэффициенты регрессии
- Распределение переменных
- Диаграмма рассеяния
- Критерии значимости
- 🎥 Видео
Видео:Эконометрика. Линейная парная регрессияСкачать

Понятие линейной регрессии. Парная линейная регрессия
Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x) , когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.
Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.
Если установленная зависимость может быть записана в виде уравнения прямой
то эта регрессионная зависимость называется линейной регрессией.
О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).
В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.
В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель




N — число элементов генеральной совокупности.
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.
Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности 



В результате получаем уравнение парной линейной регрессии выборки


n — размер выборки.
Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде

Видео:Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

Уравнение парной линейной регрессии и метод наименьших квадратов
Определение коэффициентов уравнения парной линейной регрессии
Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа 


Если через 

- прямая парной линейной регрессии проходит через точку
;
- среднее значение отклонений равна нулю:
;
- значения
и
не связаны:
.
Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:


Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).
Решение. Используем рассчитанные в решении названного выше примера суммы:
Используя эти суммы, вычислим коэффициенты:
Таким образом получили уравнение прямой парной линейной регрессии:
Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение
Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:




Видео:Линейная регрессия. Оценка качества моделиСкачать

Анализ качества модели линейной регрессии
Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.
Коэффициент детерминации
Коэффициент детерминации 




Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.
F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):
где m — число объясняющих переменных.
Сумма квадратов остатков
Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:

остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.
В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.
Стандартная ошибка регрессии
Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:
Чем меньше значение SEE, тем качественнее модель.
Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.
Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593 , SSE = 10 459,587 , SSR = 53 311,007 .
Можем убедиться, что выполняется закономерность SSR = SST — SSE :
Получаем коэффициент детерминации:

Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.
Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной
Итак, уравнение парной линейной регрессии:

В этом уравнении a — свободный член, b — коэффициент при независимой переменной.
Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.
Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.
Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии 
Решение. Подставляем в уравнение парной линейной регрессии x i = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. y i = 17036,4662 .
Подставляем в уравнение парной линейной регрессии x i = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. y i = 4161,9662 .
Если доход не меняется, то x i = 0 и получаем, что потребление уменьшается на 129,5338 у.е.
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Задачи регрессионного анализа
Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.
Наиболее частые задачи регрессионного анализа:
- установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
- выявление причинных связей между переменными величинами;
- прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.
Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.
В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Видео:Линейная регрессияСкачать

Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии
Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности 
Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.
рассматривают во взаимосвязи с альтернативной гипотезой

Статистика коэффициента направления
соответствует распределению Стьюдента с числом степеней свободы v = n — 2 ,
где 
Доверительный интервал коэффициента направления прямой линейной регрессии:

Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:
Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.
Можем рассчитать, что 

Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b 1 :

Так как 


Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.
Видео:Парная регрессия: линейная зависимостьСкачать

Контрольная работа: Парная регрессия
| Название: Парная регрессия Раздел: Рефераты по математике Тип: контрольная работа Добавлен 13:41:57 15 апреля 2011 Похожие работы Просмотров: 3780 Комментариев: 22 Оценило: 4 человек Средний балл: 4.5 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| № региона | X | Y |
| 1,000 | 2,800 | 28,000 |
| 2,000 | 2,400 | 21,300 |
| 3,000 | 2,100 | 21,000 |
| 4,000 | 2,600 | 23,300 |
| 5,000 | 1,700 | 15,800 |
| 6,000 | 2,500 | 21,900 |
| 7,000 | 2,400 | 20,000 |
| 8,000 | 2,600 | 22,000 |
| 9,000 | 2,800 | 23,900 |
| 10,000 | 2,600 | 26,000 |
| 11,000 | 2,600 | 24,600 |
| 12,000 | 2,500 | 21,000 |
| 13,000 | 2,900 | 27,000 |
| 14,000 | 2,600 | 21,000 |
| 15,000 | 2,200 | 24,000 |
| 16,000 | 2,600 | 34,000 |
| 17,000 | 3,300 | 31,900 |
| 19,000 | 3,900 | 33,000 |
| 20,000 | 4,600 | 35,400 |
| 21,000 | 3,700 | 34,000 |
| 22,000 | 3,400 | 31,000 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
5. Качество уравнений оцените с помощью средней ошибки аппроксимации.
6. С помощью F-критерия Фишера определите статистическую надежность результатов регрессионного моделирования. Выберите лучшее уравнение регрессии и дайте его обоснование.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
1. Поле корреляции для:
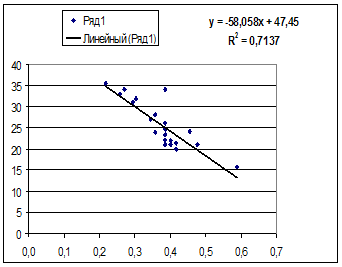
· Линейной регрессии y=a+b*x:
Гипотеза о форме связи: чем больше размер среднедушевого денежного дохода в месяц (факторный признак), тем больше при прочих равных условиях розничная продажа телевизоров (результативный признак). В данной модели параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу.
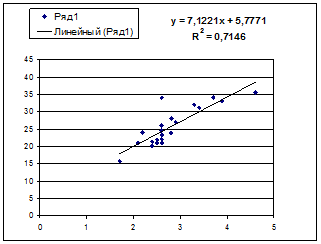
· Степенной регрессии 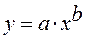
Гипотеза о форме связи : степенная функция имеет вид Y=ax b .
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1%. При х = 1 a = Y.
· Экспоненциальная регрессия 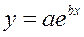
· Равносторонняя гипербола 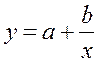
Гипотеза о форме связи: В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы: Y=a+b/x.
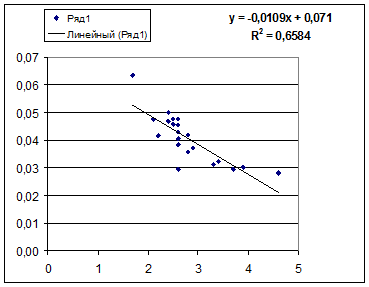
· Обратная гипербола 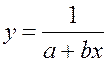
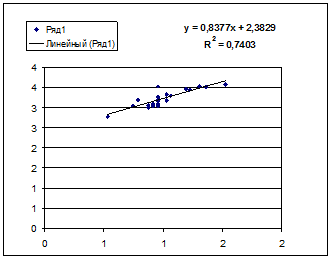
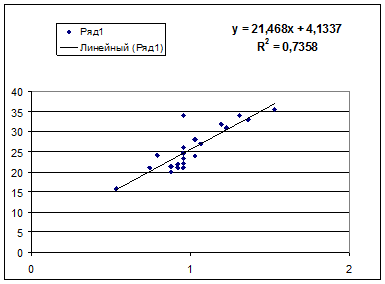
· Полулогарифмическая регрессия 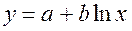
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp | Y-Y^cp | Ai |
| 1 | 2,800 | 28,000 | 78,400 | 7,840 | 784,000 | 25,719 | 2,281 | 0,081 |
| 2 | 2,400 | 21,300 | 51,120 | 5,760 | 453,690 | 22,870 | -1,570 | 0,074 |
| 3 | 2,100 | 21,000 | 44,100 | 4,410 | 441,000 | 20,734 | 0,266 | 0,013 |
| 4 | 2,600 | 23,300 | 60,580 | 6,760 | 542,890 | 24,295 | -0,995 | 0,043 |
| 5 | 1,700 | 15,800 | 26,860 | 2,890 | 249,640 | 17,885 | -2,085 | 0,132 |
| 6 | 2,500 | 21,900 | 54,750 | 6,250 | 479,610 | 23,582 | -1,682 | 0,077 |
| 7 | 2,400 | 20,000 | 48,000 | 5,760 | 400,000 | 22,870 | -2,870 | 0,144 |
| 8 | 2,600 | 22,000 | 57,200 | 6,760 | 484,000 | 24,295 | -2,295 | 0,104 |
| 9 | 2,800 | 23,900 | 66,920 | 7,840 | 571,210 | 25,719 | -1,819 | 0,076 |
| 10 | 2,600 | 26,000 | 67,600 | 6,760 | 676,000 | 24,295 | 1,705 | 0,066 |
| 11 | 2,600 | 24,600 | 63,960 | 6,760 | 605,160 | 24,295 | 0,305 | 0,012 |
| 12 | 2,500 | 21,000 | 52,500 | 6,250 | 441,000 | 23,582 | -2,582 | 0,123 |
| 13 | 2,900 | 27,000 | 78,300 | 8,410 | 729,000 | 26,431 | 0,569 | 0,021 |
| 14 | 2,600 | 21,000 | 54,600 | 6,760 | 441,000 | 24,295 | -3,295 | 0,157 |
| 15 | 2,200 | 24,000 | 52,800 | 4,840 | 576,000 | 21,446 | 2,554 | 0,106 |
| 16 | 2,600 | 34,000 | 88,400 | 6,760 | 1156,000 | 24,295 | 9,705 | 0,285 |
| 17 | 3,300 | 31,900 | 105,270 | 10,890 | 1017,610 | 29,280 | 2,620 | 0,082 |
| 19 | 3,900 | 33,000 | 128,700 | 15,210 | 1089,000 | 33,553 | -0,553 | 0,017 |
| 20 | 4,600 | 35,400 | 162,840 | 21,160 | 1253,160 | 38,539 | -3,139 | 0,089 |
| 21 | 3,700 | 34,000 | 125,800 | 13,690 | 1156,000 | 32,129 | 1,871 | 0,055 |
| 22 | 3,400 | 31,000 | 105,400 | 11,560 | 961,000 | 29,992 | 1,008 | 0,033 |
| Итого | 58,800 | 540,100 | 1574,100 | 173,320 | 14506,970 | 540,100 | 0,000 | |
| сред значение | 2,800 | 25,719 | 74,957 | 8,253 | 690,808 | 0,085 | ||
| станд. откл | 0,643 | 5,417 |
Система нормальных уравнений составит:
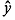
· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели 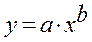
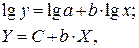
Для расчетов используем данные табл. 3:
| № рег | X | Y | XY | X^2 | Y^2 | Yp^cp | y^cp |
| 1 | 1,030 | 3,332 | 3,431 | 1,060 | 11,104 | 3,245 | 25,67072 |
| 2 | 0,875 | 3,059 | 2,678 | 0,766 | 9,356 | 3,116 | 22,56102 |
| 3 | 0,742 | 3,045 | 2,259 | 0,550 | 9,269 | 3,004 | 20,17348 |
| 4 | 0,956 | 3,148 | 3,008 | 0,913 | 9,913 | 3,183 | 24,12559 |
| 5 | 0,531 | 2,760 | 1,465 | 0,282 | 7,618 | 2,827 | 16,90081 |
| 6 | 0,916 | 3,086 | 2,828 | 0,840 | 9,526 | 3,150 | 23,34585 |
| 7 | 0,875 | 2,996 | 2,623 | 0,766 | 8,974 | 3,116 | 22,56102 |
| 8 | 0,956 | 3,091 | 2,954 | 0,913 | 9,555 | 3,183 | 24,12559 |
| 9 | 1,030 | 3,174 | 3,268 | 1,060 | 10,074 | 3,245 | 25,67072 |
| 10 | 0,956 | 3,258 | 3,113 | 0,913 | 10,615 | 3,183 | 24,12559 |
| 11 | 0,956 | 3,203 | 3,060 | 0,913 | 10,258 | 3,183 | 24,12559 |
| 12 | 0,916 | 3,045 | 2,790 | 0,840 | 9,269 | 3,150 | 23,34585 |
| 13 | 1,065 | 3,296 | 3,509 | 1,134 | 10,863 | 3,275 | 26,4365 |
| 14 | 0,956 | 3,045 | 2,909 | 0,913 | 9,269 | 3,183 | 24,12559 |
| 15 | 0,788 | 3,178 | 2,506 | 0,622 | 10,100 | 3,043 | 20,97512 |
| 16 | 0,956 | 3,526 | 3,369 | 0,913 | 12,435 | 3,183 | 24,12559 |
| 17 | 1,194 | 3,463 | 4,134 | 1,425 | 11,990 | 3,383 | 29,4585 |
| 19 | 1,361 | 3,497 | 4,759 | 1,852 | 12,226 | 3,523 | 33,88317 |
| 20 | 1,526 | 3,567 | 5,443 | 2,329 | 12,721 | 3,661 | 38,90802 |
| 21 | 1,308 | 3,526 | 4,614 | 1,712 | 12,435 | 3,479 | 32,42145 |
| 22 | 1,224 | 3,434 | 4,202 | 1,498 | 11,792 | 3,408 | 30,20445 |
| итого | 21,115 | 67,727 | 68,921 | 22,214 | 219,361 | 67,727 | 537,270 |
| сред зн | 1,005 | 3,225 | 3,282 | 1,058 | 10,446 | 3,225 | |
| стан откл | 0,216 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: 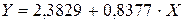
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y .
· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели 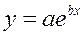
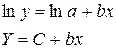
Для расчетов используем данные табл. 4:
| № региона | X | Y | XY | X^2 | Y^2 | Yp | y^cp |
| 1 | 2,800 | 3,332 | 9,330 | 7,840 | 11,104 | 3,225 | 25,156 |
| 2 | 2,400 | 3,059 | 7,341 | 5,760 | 9,356 | 3,116 | 22,552 |
| 3 | 2,100 | 3,045 | 6,393 | 4,410 | 9,269 | 3,034 | 20,777 |
| 4 | 2,600 | 3,148 | 8,186 | 6,760 | 9,913 | 3,170 | 23,818 |
| 5 | 1,700 | 2,760 | 4,692 | 2,890 | 7,618 | 2,925 | 18,625 |
| 6 | 2,500 | 3,086 | 7,716 | 6,250 | 9,526 | 3,143 | 23,176 |
| 7 | 2,400 | 2,996 | 7,190 | 5,760 | 8,974 | 3,116 | 22,552 |
| 8 | 2,600 | 3,091 | 8,037 | 6,760 | 9,555 | 3,170 | 23,818 |
| 9 | 2,800 | 3,174 | 8,887 | 7,840 | 10,074 | 3,225 | 25,156 |
| 10 | 2,600 | 3,258 | 8,471 | 6,760 | 10,615 | 3,170 | 23,818 |
| 11 | 2,600 | 3,203 | 8,327 | 6,760 | 10,258 | 3,170 | 23,818 |
| 12 | 2,500 | 3,045 | 7,611 | 6,250 | 9,269 | 3,143 | 23,176 |
| 13 | 2,900 | 3,296 | 9,558 | 8,410 | 10,863 | 3,252 | 25,853 |
| 14 | 2,600 | 3,045 | 7,916 | 6,760 | 9,269 | 3,170 | 23,818 |
| 15 | 2,200 | 3,178 | 6,992 | 4,840 | 10,100 | 3,061 | 21,352 |
| 16 | 2,600 | 3,526 | 9,169 | 6,760 | 12,435 | 3,170 | 23,818 |
| 17 | 3,300 | 3,463 | 11,427 | 10,890 | 11,990 | 3,362 | 28,839 |
| 19 | 3,900 | 3,497 | 13,636 | 15,210 | 12,226 | 3,526 | 33,978 |
| 20 | 4,600 | 3,567 | 16,407 | 21,160 | 12,721 | 3,717 | 41,140 |
| 21 | 3,700 | 3,526 | 13,048 | 13,690 | 12,435 | 3,471 | 32,170 |
| 22 | 3,400 | 3,434 | 11,676 | 11,560 | 11,792 | 3,389 | 29,638 |
| Итого | 58,800 | 67,727 | 192,008 | 173,320 | 219,361 | 67,727 | 537,053 |
| сред зн | 2,800 | 3,225 | 9,143 | 8,253 | 10,446 | ||
| стан откл | 0,643 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: 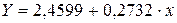
Для расчета теоретических значений y подставим в уравнение 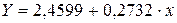
· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели 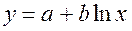
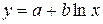
Для расчетов используем данные табл. 5:
| № региона | X | Y | XY | X^2 | Y^2 | y^cp |
| 1 | 1,030 | 28,000 | 28,829 | 1,060 | 784,000 | 26,238 |
| 2 | 0,875 | 21,300 | 18,647 | 0,766 | 453,690 | 22,928 |
| 3 | 0,742 | 21,000 | 15,581 | 0,550 | 441,000 | 20,062 |
| 4 | 0,956 | 23,300 | 22,263 | 0,913 | 542,890 | 24,647 |
| 5 | 0,531 | 15,800 | 8,384 | 0,282 | 249,640 | 15,525 |
| 6 | 0,916 | 21,900 | 20,067 | 0,840 | 479,610 | 23,805 |
| 7 | 0,875 | 20,000 | 17,509 | 0,766 | 400,000 | 22,928 |
| 8 | 0,956 | 22,000 | 21,021 | 0,913 | 484,000 | 24,647 |
| 9 | 1,030 | 23,900 | 24,608 | 1,060 | 571,210 | 26,238 |
| 10 | 0,956 | 26,000 | 24,843 | 0,913 | 676,000 | 24,647 |
| 11 | 0,956 | 24,600 | 23,506 | 0,913 | 605,160 | 24,647 |
| 12 | 0,916 | 21,000 | 19,242 | 0,840 | 441,000 | 23,805 |
| 13 | 1,065 | 27,000 | 28,747 | 1,134 | 729,000 | 26,991 |
| 14 | 0,956 | 21,000 | 20,066 | 0,913 | 441,000 | 24,647 |
| 15 | 0,788 | 24,000 | 18,923 | 0,622 | 576,000 | 21,060 |
| 16 | 0,956 | 34,000 | 32,487 | 0,913 | 1156,000 | 24,647 |
| 17 | 1,194 | 31,900 | 38,086 | 1,425 | 1017,610 | 29,765 |
| 19 | 1,361 | 33,000 | 44,912 | 1,852 | 1089,000 | 33,351 |
| 20 | 1,526 | 35,400 | 54,022 | 2,329 | 1253,160 | 36,895 |
| 21 | 1,308 | 34,000 | 44,483 | 1,712 | 1156,000 | 32,221 |
| 22 | 1,224 | 31,000 | 37,937 | 1,498 | 961,000 | 30,406 |
| Итого | 21,115 | 540,100 | 564,166 | 22,214 | 14506,970 | 540,100 |
| сред зн | 1,005 | 25,719 | 26,865 | 1,058 | 690,808 | |
| стан откл | 0,216 | 5,417 |
Рассчитаем a и b:
Получим линейное уравнение: 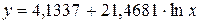
· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель 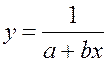
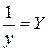
Для расчетов используем данные табл. 6:
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 2,800 | 0,036 | 0,100 | 7,840 | 0,001 | 24,605 |
| 2 | 2,400 | 0,047 | 0,113 | 5,760 | 0,002 | 22,230 |
| 3 | 2,100 | 0,048 | 0,100 | 4,410 | 0,002 | 20,729 |
| 4 | 2,600 | 0,043 | 0,112 | 6,760 | 0,002 | 23,357 |
| 5 | 1,700 | 0,063 | 0,108 | 2,890 | 0,004 | 19,017 |
| 6 | 2,500 | 0,046 | 0,114 | 6,250 | 0,002 | 22,780 |
| 7 | 2,400 | 0,050 | 0,120 | 5,760 | 0,003 | 22,230 |
| 8 | 2,600 | 0,045 | 0,118 | 6,760 | 0,002 | 23,357 |
| 9 | 2,800 | 0,042 | 0,117 | 7,840 | 0,002 | 24,605 |
| 10 | 2,600 | 0,038 | 0,100 | 6,760 | 0,001 | 23,357 |
| 11 | 2,600 | 0,041 | 0,106 | 6,760 | 0,002 | 23,357 |
| 12 | 2,500 | 0,048 | 0,119 | 6,250 | 0,002 | 22,780 |
| 13 | 2,900 | 0,037 | 0,107 | 8,410 | 0,001 | 25,280 |
| 14 | 2,600 | 0,048 | 0,124 | 6,760 | 0,002 | 23,357 |
| 15 | 2,200 | 0,042 | 0,092 | 4,840 | 0,002 | 21,206 |
| 16 | 2,600 | 0,029 | 0,076 | 6,760 | 0,001 | 23,357 |
| 17 | 3,300 | 0,031 | 0,103 | 10,890 | 0,001 | 28,398 |
| 19 | 3,900 | 0,030 | 0,118 | 15,210 | 0,001 | 34,844 |
| 20 | 4,600 | 0,028 | 0,130 | 21,160 | 0,001 | 47,393 |
| 21 | 3,700 | 0,029 | 0,109 | 13,690 | 0,001 | 32,393 |
| 22 | 3,400 | 0,032 | 0,110 | 11,560 | 0,001 | 29,301 |
| Итого | 58,800 | 0,853 | 2,296 | 173,320 | 0,036 | 537,933 |
| сред знач | 2,800 | 0,041 | 0,109 | 8,253 | 0,002 | |
| стан отклон | 0,643 | 0,009 |
Рассчитаем a и b:
Получим линейное уравнение: 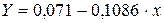
Для расчета теоретических значений y подставим в уравнение 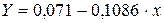
· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы 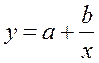
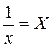
Для расчетов используем данные табл. 7:
| № региона | X=1/z | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 0,357 | 28,000 | 10,000 | 0,128 | 784,000 | 26,715 |
| 2 | 0,417 | 21,300 | 8,875 | 0,174 | 453,690 | 23,259 |
| 3 | 0,476 | 21,000 | 10,000 | 0,227 | 441,000 | 19,804 |
| 4 | 0,385 | 23,300 | 8,962 | 0,148 | 542,890 | 25,120 |
| 5 | 0,588 | 15,800 | 9,294 | 0,346 | 249,640 | 13,298 |
| 6 | 0,400 | 21,900 | 8,760 | 0,160 | 479,610 | 24,227 |
| 7 | 0,417 | 20,000 | 8,333 | 0,174 | 400,000 | 23,259 |
| 8 | 0,385 | 22,000 | 8,462 | 0,148 | 484,000 | 25,120 |
| 9 | 0,357 | 23,900 | 8,536 | 0,128 | 571,210 | 26,715 |
| 10 | 0,385 | 26,000 | 10,000 | 0,148 | 676,000 | 25,120 |
| 11 | 0,385 | 24,600 | 9,462 | 0,148 | 605,160 | 25,120 |
| 12 | 0,400 | 21,000 | 8,400 | 0,160 | 441,000 | 24,227 |
| 13 | 0,345 | 27,000 | 9,310 | 0,119 | 729,000 | 27,430 |
| 14 | 0,385 | 21,000 | 8,077 | 0,148 | 441,000 | 25,120 |
| 15 | 0,455 | 24,000 | 10,909 | 0,207 | 576,000 | 21,060 |
| 16 | 0,385 | 34,000 | 13,077 | 0,148 | 1156,000 | 25,120 |
| 17 | 0,303 | 31,900 | 9,667 | 0,092 | 1017,610 | 29,857 |
| 19 | 0,256 | 33,000 | 8,462 | 0,066 | 1089,000 | 32,564 |
| 20 | 0,217 | 35,400 | 7,696 | 0,047 | 1253,160 | 34,829 |
| 21 | 0,270 | 34,000 | 9,189 | 0,073 | 1156,000 | 31,759 |
| 22 | 0,294 | 31,000 | 9,118 | 0,087 | 961,000 | 30,374 |
| Итого | 7,860 | 540,100 | 194,587 | 3,073 | 14506,970 | 540,100 |
| сред знач | 0,374 | 25,719 | 9,266 | 0,146 | 1318,815 | |
| стан отклон | 0,079 | 25,639 |
Рассчитаем a и b:
Получим линейное уравнение: 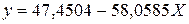
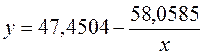
3. Оценка тесноты связи с помощью показателей корреляции и детерминации :
· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции rxy =b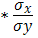
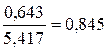
· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции 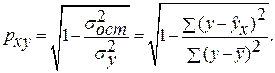
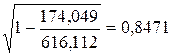
· Экспоненциальная модель. Был получен следующий индекс корреляции ρxy =0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy =0,66. Это означает, что 66% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy =0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,58% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Гиперболическая модель. Был получен следующий индекс корреляции ρxy =0,8448 и коэффициент корреляции rxy =-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Обратная модель. Был получен следующий индекс корреляции ρxy =0,8114 и коэффициент корреляции rxy =-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,6584. Это означает, что 65,84% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy =0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Рассчитаем коэффициент эластичности для линейной модели:
· Для уравнения прямой:y = 5,777+7,122∙x
· Для уравнениястепенноймодели 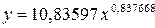
· Для уравненияэкспоненциальноймодели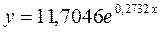
Для уравненияполулогарифмическоймодели 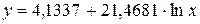
· Для уравнения обратной гиперболической модели 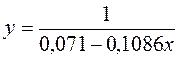
· Для уравнения равносторонней гиперболической модели 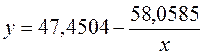
Сравнивая значения 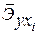
·
·
·
·
·
·
Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.
5. Оценка качества уравнений с помощью средней ошибки аппроксимации.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения 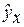
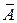
В среднем расчетные значения отклоняются от фактических на:
· Линейная регрессия. 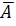
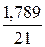
Качество построенной модели оценивается как хорошее, так как 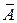
· Степенная регрессия. 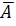
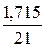
Качество построенной модели оценивается как хорошее, так как 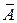
· Экспоненциальная регрессия. 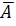
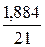
Качество построенной модели оценивается как хорошее, так как 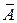
· Полулогарифмическая регрессия. 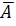
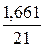
Качество построенной модели оценивается как хорошее, так как 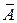
· Гиперболическая регрессия. 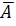
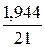
Качество построенной модели оценивается как хорошее, так как 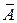
· Обратная регрессия. 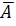
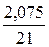
Качество построенной модели оценивается как хорошее, так как 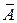
6. Рассчитаем F-критерий:
· Линейная регрессия. 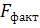
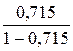
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Основы линейной регрессии
Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Видео:Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Видео:Парная нелинейная регрессияСкачать

Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Между
и
существует линейное соотношение: для любых пар
данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.
- Остатки нормально распределены с нулевым средним значением;
- Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин
Если нанести остатки против предсказанных величин
от
мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением
то это допущение не выполняется;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Видео:МНК. Пример 2. Парная регрессияСкачать

Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Видео:Математика #1 | Корреляция и регрессияСкачать

Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Видео:Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Видео:Лекция 8. Линейная регрессияСкачать

Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Видео:Парная и множественная линейная регрессияСкачать
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Видео:Регрессия в ExcelСкачать

Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:
Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:
Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии
Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .
Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»
Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.
Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости
Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
🎥 Видео
Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

Построение регрессионных моделей в R. Оценка точности и адекватности моделейСкачать




 ;
; ;
; и
и  не связаны:
не связаны:  .
.












 ,
,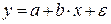 .
.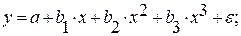
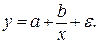
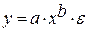 ;
;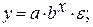
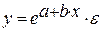
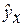 минимальна, т.е.
минимальна, т.е.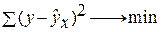
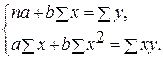
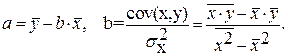
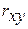 для линейной регрессии
для линейной регрессии 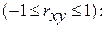
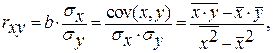
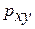 — для нелинейной регрессии (
— для нелинейной регрессии (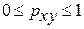 ):
):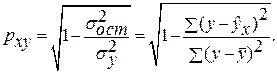
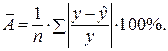
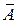 – не более 8 – 10%.
– не более 8 – 10%.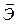 показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения: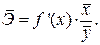
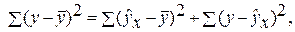
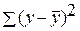 – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений;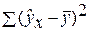 – сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
– сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);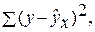 –остаточная сумма квадратов отклонений.
–остаточная сумма квадратов отклонений.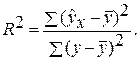
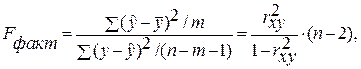
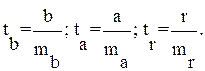
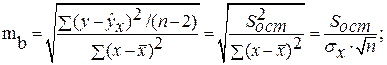
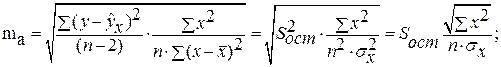
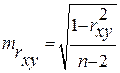
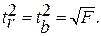
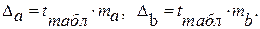

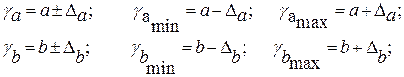
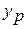 определяется путем подстановки в уравнение регрессии
определяется путем подстановки в уравнение регрессии 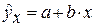 соответствующего (прогнозного) значения
соответствующего (прогнозного) значения 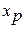 . Вычисляется средняя стандартная ошибка прогноза
. Вычисляется средняя стандартная ошибка прогноза 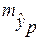 :
: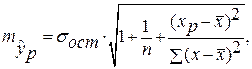 где
где 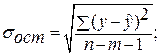
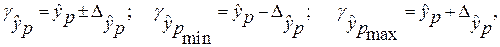 где
где