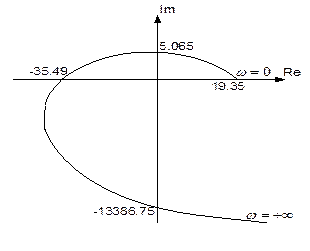Оценить устойчивость по критерию михайлова системы с характеристическим уравнением (4 видео)

Пример определения устойчивости САУ с помощью критерия Михайлова

Необходимо определить устойчивость САУ, структурная схема которой представлена на рисунке 65, числовые значения данных представлены в таблице на рисунке 66.

Решение:

Характеристическое уравнение данной системы имеет вид:

D(s) = 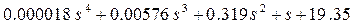(2.42.)

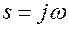
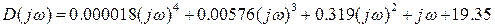
Подставив в уравнение , получим:

(2.45.)

Преобразуем уравнение в следующий вид:

(2.46.)

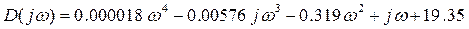
Выделим действительную и мнимую части:

; (2.47.)

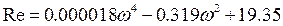
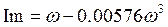
Для построения годографа Михайлова составим таблицу значений (рисунок 70):

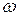7.817	13.176	132.9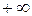
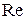19.35	−35.49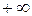
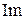5.0654	−13386.75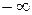

Рис.70. Таблица значений

С помощью таблицы значений построим на комплексной плоскости годограф Михайлова и представим его на рисунке 71.

Рис.71. Годограф Михайлова

Анализируя годограф на рисунке 71 в соответствии с критерием Михайлова можно сделать вывод, что САУ устойчива, т.к. годограф начинается на действительной оси и с ростом ω от 0 до 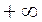обходит последовательно в положительном направлении 4 квадранта комплексной плоскости.

Критерий Найквиста

В 1932 г. американский физик Найквист сформулировал критерий устойчивости САУ, позволяющий судить об устойчивости замкнутой системы по АФЧХ ее разомкнутого контура. Критерий Найквиста сформулирован следующим образом – если САУ устойчива в разомкнутом состоянии, то необходимым и достаточным условием ее устойчивости в замкнутом состоянии будет условие, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до+ ¥ не охватывала на комплексной плоскости точку с координатами (-1; j0).

Из определения разомкнутой системы вытекает, что входная величина системы является входной величиной первого звена прямой цепи, а выходной величиной разомкнутой системы является выходная величина последнего звена цепи обратной связи. Для замкнутой системы передаточная функция разомкнутой системы примет следующий вид:

(2.48.)

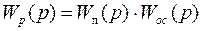
Заменив в формуле передаточной функции разомкнутой системы (2.48.)

р = jw, получим АФЧХ разомкнутой системы n — ного порядка:

(2.49.)

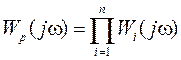
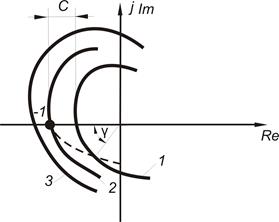
Указанную АФЧХ разомкнутой системы построим на комплексной плоскости при увеличении частоты от 0до +¥, что показано на рисунке 72.

Рис.72. Критерий устойчивости Найквиста:

1 – АФЧХ устойчивой системы, 2 – АФЧХ системы на границе

устойчивости, 3 – АФЧХ неустойчивой системы

В случае, когда АФЧХ разомкнутой системы пройдет через точку с координатами

(-1; j0), как видно из рисунка 72 (график 2), система будет находиться на колебательной границе устойчивости. В случае, когда АФЧХ разомкнутой системы будет охватывать точку с координатами (-1; j0), замкнутая система будет являться неустойчивой (рисунок 72, график 3).

Дата добавления: 2016-02-04 ; просмотров: 5255 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Теория автоматического управления. Лекция 10. Критерий МихайловаСкачать

КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА

Это частотный критерий устойчивости, который был сформулирован в 1938 г. советским ученым А.В. Михайловым. Он основан на рассмотрении комплексного полинома F(/co), который получается заменой р на /со в характеристическом полиноме Л<р):

Выделим в комплексном полиноме действительную и мнимую части:

При конкретном численном значении частоты со = со, значение комплексного полинома F(/co_f) можно изобразить на комплексной плоскости в виде вектора, соединяющего начало координат с точкой

<ЯДсо,); /Дсо_;.)>. При изменении со от 0 до оо конец вектора F(yco) описывает некоторую кривую, которую называют годографом Михайлова (рис. 4.3). Причем начинается годограф из точки (я₀;0); в этом нетрудно убедиться, подставив нулевое значение частоты в (4.4).

Рис. 4.3. Примеры годографов Михайлова для устойчивых САУ различного порядка (а) и неустойчивых САУ пятого порядка (б)

Критерий Михайлова формулируется следующим образом: для устойчивости линейной системы п-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении со от 0 до оо начинался на вещественной положительной полуоси и проходил последовательно против часовой стрелки п квадрантов, не обращаясь в нуль и стремясь к со в п-м квадранте.

Для доказательства критерия проанализируем, как связаны корни характеристического полинома с видом годографа Михайлова. Представим полином как произведение сомножителей:

Тогда комплексный полином F(yco) примет вид

Если характеристическое уравнение системы содержит нулевой корень, то при со = 0 соответствующий сомножитель обратится в О, т. е. годограф будет начинаться из точки 0. Если имеются два чисто мнимых корня ±усо₀, то при определенном значении частоты со = со₀

один из сомножителей также обратится в 0, и годограф пройдет через начало координат.

В случае устойчивой системы все корни характеристического уравнения имеют отрицательную вещественную часть, и, следовательно, годограф Михайлова не обращается в нуль.

Определим угол поворота вектора F(yco) при изменении частоты от 0 до оо. Для этого предварительно рассмотрим векторы, соответствующие отдельным сомножителям в выражении (4.5). Угол поворота вектора для каждого сомножителя будет зависеть от вида корня характеристического уравнения; при этом можно выделить следующие четыре случая.

• Корень характеристического уравнения вещественный отрицательный: р_к = -а_к, а_к > 0 . Соответствующий сомножитель в (4.5) имеет вид F_k(j(o) = (j(o + a_k). При изменении со от 0 до оо конец вектора F_k(j(o) перемещается из точки F_k (0) = а_к вверх по прямой, параллельной оси ординат (рис. 4.4, а). Изменение фазы F_k(j(o) составляет +90°.

Рис. 4.4. Годографы векторов F_k (усо) для сомножителей, соответствующих отрицательному (а) и положительному (б) вещественным корням

• Корень характеристического уравнения вещественный положительный: р_к = +а_к, а_к > 0 . Соответствующий сомножитель в (4.5) имеет вид F_k(j(o) = (j(o-a_k). При изменении со от 0 до оо конец вектора F_k (усо) перемещается из точки F_k (0) = -а_к вверх по прямой, параллельной оси ординат (рис. 4.4, б). Изменение фазы F_k(jсо) составляет -90°.

• Пара комплексно-сопряженных корней с отрицательной вещественной частью: р_кк+х = -а_к ± j$_k., а_к >0, Р_А >0. Соответствующие сомножители в (4.5) имеют вид

У векторов F_k (j со) и F_k+X (у со) начальные фазы по модулю одинаковы, но имеют противоположные знаки. При изменении со от 0 до оо один вектор поворачивается на угол ф₀ + 90°, а второй — на угол -ср₀ + 90° (рис. 4.5, а). Суммарный угол поворота для пары сомножителей равен +180°.

Рис. 4.5. Годографы векторов F_k(jсо) для сомножителей, соответствующих комплексно-сопряженным корням с отрицательной (а) и положительной (б)

• Пара комплексно-сопряженных корней с положительной вещественной частью: р_к А+1 — а_к ± у(3_А, а_А>0, Р_А>0. Соответствующие сомножители в (4.5) имеют вид

При изменении со от 0 до оо суммарный угол поворота для пары сомножителей равен -180° (рис. 4.5, б).

Для определения фазы комплексного полинома F(jсо) представим его в показательной форме:

Следовательно, общая фаза F(jсо) равна сумме фаз отдельных

Таким образом, в устойчивой системе, т. е. когда все корни характеристического уравнения имеют отрицательную вещественную часть, каждый из п корней при изменении со от 0 до оо даст приращение фазы Дер* = +90°, а общий угол поворота F(yco) составит п -90°. То есть годограф пройдет п квадрантов в положительном направлении (против часовой стрелки), ав n-м квадранте уйдет в бесконечность.

Если система неустойчива, то общий угол поворота составит меньше п • 90°, как минимум, на 180°.

Как показано в ходе доказательства, условием границы устойчивости для критерия Михайлова является обращение годографа в нуль при некотором значении частоты со = со₀. Если годограф начинается из точки 0 (со₀ = 0), то имеет место апериодическая граница устойчивости, а при со₀ > 0 — колебательная, причем со₀ — частота незатухающих колебаний, возникающих в системе.

Проверить с помощью критерия Михайлова устойчивость системы, передаточная функция которой имеет вид

Запишем характеристический полином системы и соответствующий ему комплексный полином:

Для построения годографа рассчитаем значения F(jсо) при различных со (см. табл. 4.1)

Видео:ЛСАР Лекция №10 Критерий МихайловаСкачать

КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА

Критерий устойчивости Михайлова относится к частотным критериям и используется для исследования устойчивости замкнутых систем. Рассмотрим замкнутую систему управления структурная схема которой имеет вид

Пусть передаточная функция разомкнутой системы равна

и пусть — степень полинома , — степень полинома .

Передаточная функция замкнутой системы

Полином — имеем степень -степень полинома

Составим характеристический полином замкнутой системы

Если подставим в , то получим комплексное число

В последнем равенстве выделим действительную и мнимую части комплексного числа:

На плоскости и комплексное число изображается вектором (см. рис. 2). При из изменении частоты от 0 до вектор изменяется по величине и направлению. Конец вектора в комплексной плоскости описывает некоторую кривую, которая называется годографом Михайлова.

Формулировка критерия Михайлова.

Для того, чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно чтобы годограф Михайлова при изменении частоты от 0 до , начинался при на вещественной положительной полуоси, обходил последовательно квадрантов координатной плоскости против часовой стрелки, где — порядок характеристического полинома.

Заметим, что для устойчивых систем автоматического управления годограф Михайлова начинается при на вещественной положительной полуоси, поскольку, поскольку все коэффициенты характеристического полинома положительны и .

Кроме того, для устойчивых систем фаза с ростом частоты должна возрастать монотонно, т.е. вектор должен поворачиваться только против стрелки, поскольку с ростом частоты монотонно возрастают имеющие одинаковые знаки фазы элементарных векторов ,являющиеся слагаемыми вектора .

Кривая Михайлова для устойчивых систем всегда плавную спиралевидную форму, причём конец её () уходит в бесконечность в том квадранте координатной плоскости, номер которого равен степени характеристического полинома.

Типовые кривые Михайлова для устойчивых систем, имеющих характеристический полином степеней , , , и представлены на рисунке 3 ( — во всех случаях приняты одинаковыми).

Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов координатной плоскости, вследствие чего угол поворота вектора оказывается меньшим, чем

Примеры годографов Михайлова для неустойчивых систем:

Другая формулировка критерий устойчивости Михайлова.

Система автоматического управления устойчива тогда и только тогда, когда уравнения и имеют все действительные и перемежающиеся корни, причём общее число этих корней равно порядку характеристического уравнения и при выполняется неравенства и .

Это условие устойчивости системы получило также название условие перемежаемости корней.

Правило исследования устойчивости систем автоматического управления с помощью критерия Михайлова. Для исследования устойчивости линейных систем автоматического управления с помощью критерия Михайлова надо:

Преобразовать структурную схему исследуемой системы к расчётной структурной схеме

и определить передаточную функцию разомкнутой системы .

По передаточной функции разомкнутой системы получить передаточную функцию замкнутой системы

и вычислить характеристический полином замкнутой системы

3. В характеристическом полиноме подставить

и выделить в комплексном числе действительную и мнимую части

Используя полученные выражения для и строим годограф Михайлова, изменяя значения частоты от 0 до .

5. Используя критерий Михайлова, по построенному годографу определяем устойчивость системы управления.

Пример. С помощью критерия Михайлова определить устойчивость замкнутой системы с передаточной функцией

Решение. Характеристический полином замкнутой системы:

Годограф Михайлова.

Условие перемежаемости корней:

Определение границ устойчивости.

Характеристический полином замкнутой системы автоматического управления

Система автоматического управления будет находиться на границе устойчивости, если характеристический полином замкнутой системы имеет пару чисто мнимых корней , , а остальные корня имеют отрицательные действительные части.

Подставим в характеристический полином и выделим действительную и мнимую части комплексного числа :

(т.к. , то считаем, что это корень характеристического уравнения).

Если система находится на границе устойчивости, то годограф Михайлова для системы проходит через начало координат (см. рис. 7).

Решение системы уравнений , позволяет установить взаимосвязь параметров замкнутой системы и частоты гармонических колебаний , для случая, когда система будет находиться на границе устойчивости. Если при изменении параметров годограф пойдёт так, как показано на рисунке (кривая 1), то система будет устойчивой, если так как на кривой 2 — то система будет неустойчивой.

Пример. С помощью критерия устойчивости Михайлова определить границу устойчивости для системы расчётная структурная схема которой показана на рисунке. устойчивость автоматический линейный постоянство

Решение. Передаточная функция замкнутой системы имеет вид:

Полагая характеристическое уравнение приобретает вид:

Решение этой системы даёт уравнение границы устойчивости.

Уравнение границы устойчивости

Функция двух переменных и — параметров системы. Изменим значение коэффициента усиления на , т.е. , а значение оставим без изменения. Тогда для имеем

то в зависимости от знака годограф может занять одно из 2-х положений

Если , то годограф Михайлова охватывает начало координат и система устойчива. Если , то годограф Михайлова не охватывает начало координат, критерий Михайлова не выполняется и система устойчива. Это значит, что для обеспечения устойчивости системы коэффициент усиления системы должен удовлетворять неравенству . Таким образом, система устойчива, если