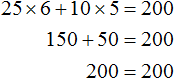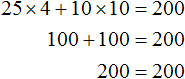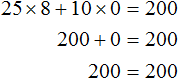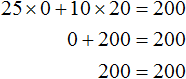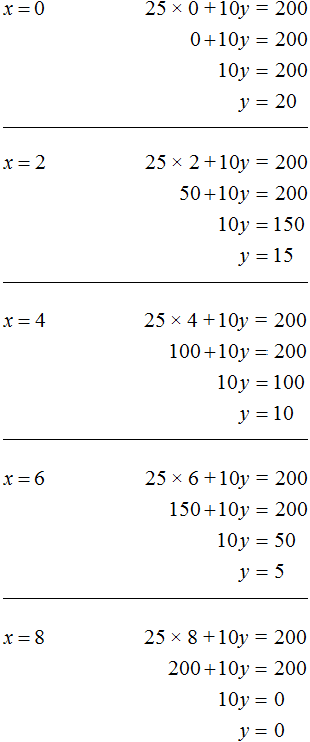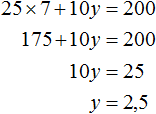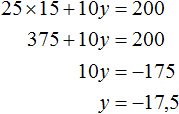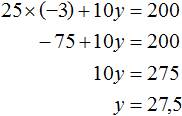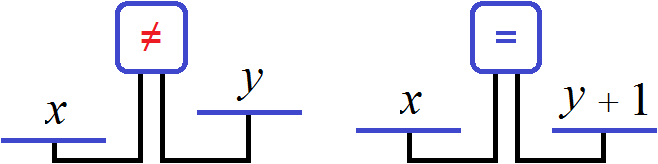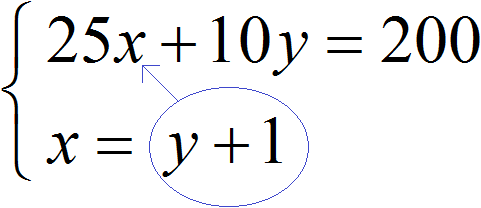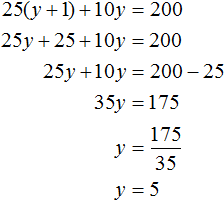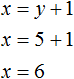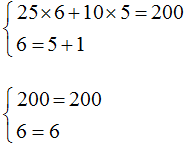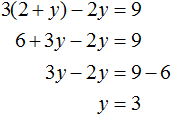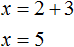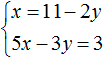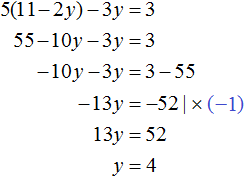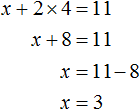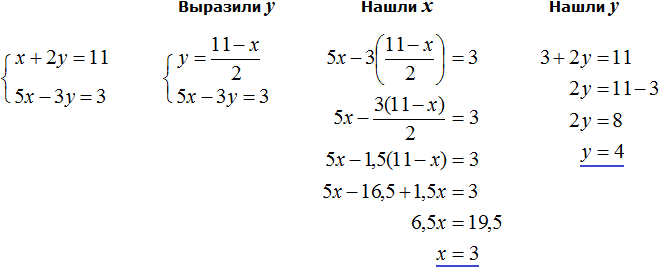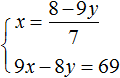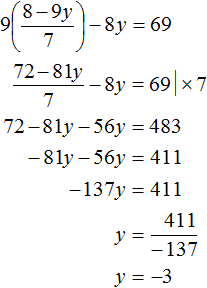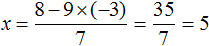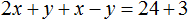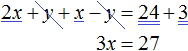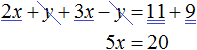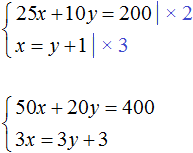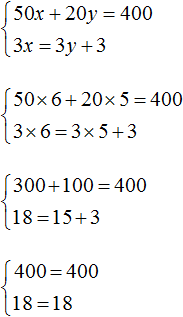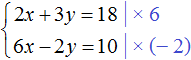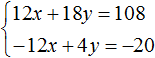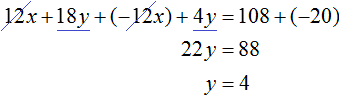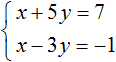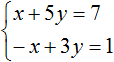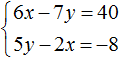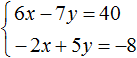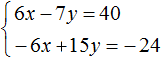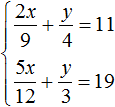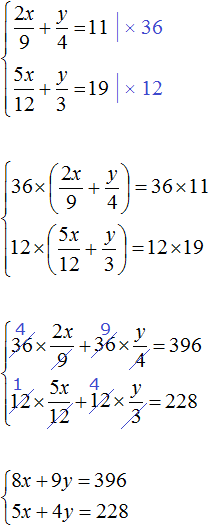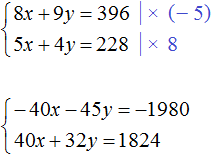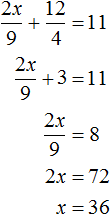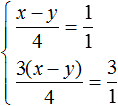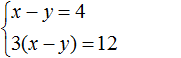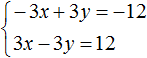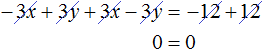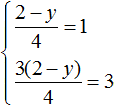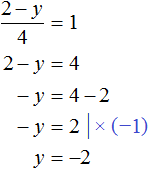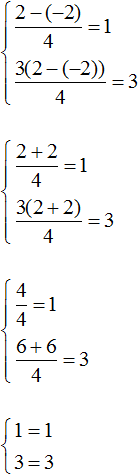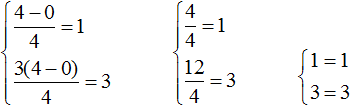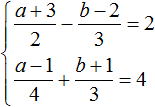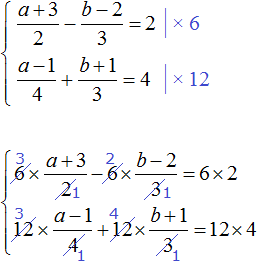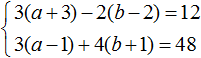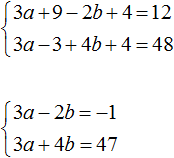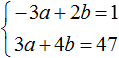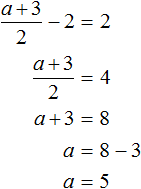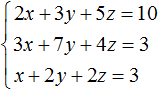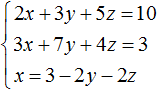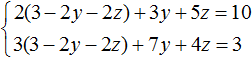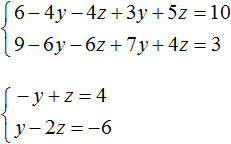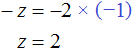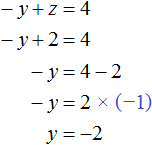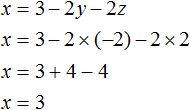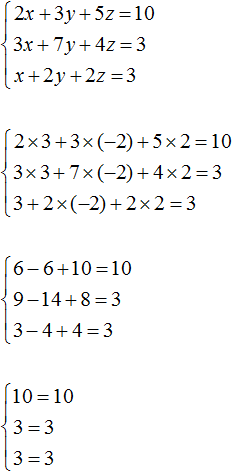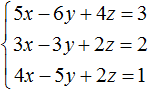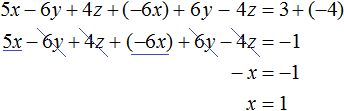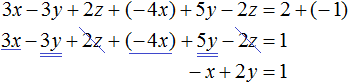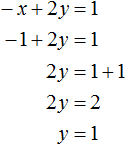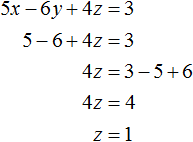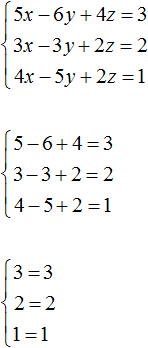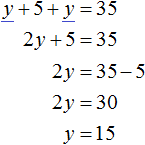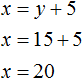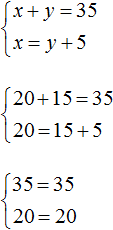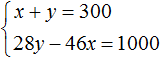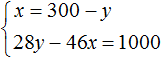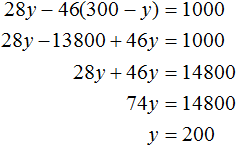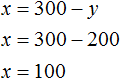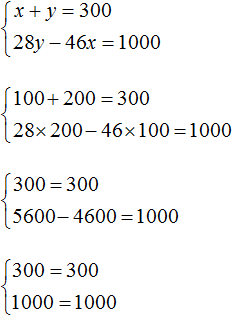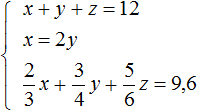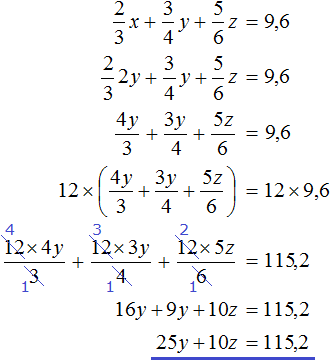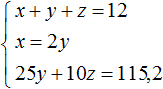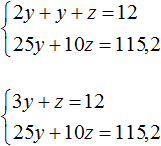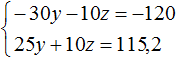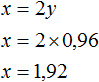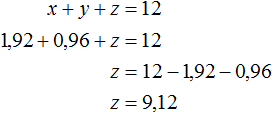- Линейные уравнения с двумя переменными
- Система двух линейных уравнений с двумя переменными
- Метод подстановки
- Метод сложения
- Система линейных уравнений с тремя переменными
- Задачи на составление систем линейных уравнений
- Системы линейных уравнений
- Системы линейных уравнений. Понятия линейного уравнения и системы линейных уравнений
- Пример №15
- Метод Гаусса решения систем линейных уравнений
- Пример №16
- Пример №17
- Пример №18
- Как решать систему уравнений
- Основные понятия
- Линейное уравнение с двумя переменными
- Система двух линейных уравнений с двумя переменными
- Метод подстановки
- Пример 1
- Пример 2
- Пример 3
- Метод сложения
- Система линейных уравнений с тремя переменными
- Решение задач
- Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
- Задание 2. Как решать систему уравнений способом подстановки
- Задание 3. Как решать систему уравнений методом сложения
- Задание 4. Решить систему уравнений
- Задание 5. Как решить систему уравнений с двумя неизвестными
- 📽️ Видео
Видео:Системы уравнений. Способ уравнивания коэффициентов - 1Скачать

Линейные уравнения с двумя переменными
У школьника имеется 200 рублей, чтобы пообедать в школе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе можно накупить на 200 рублей?
Обозначим количество пирожных через x , а количество чашек кофе через y . Тогда стоимость пирожных будет обозначаться через выражение 25x , а стоимость чашек кофе через 10y .
25x — стоимость x пирожных
10y — стоимость y чашек кофе
Итоговая сумма должна равняться 200 рублей. Тогда получится уравнение с двумя переменными x и y
Сколько корней имеет данное уравнение?
Всё зависит от аппетита школьника. Если он купит 6 пирожных и 5 чашек кофе, то корнями уравнения будут числа 6 и 5.
Говорят, что пара значений 6 и 5 являются корнями уравнения 25x + 10y = 200 . Записывается как (6; 5) , при этом первое число является значением переменной x , а второе — значением переменной y .
6 и 5 не единственные корни, которые обращают уравнение 25x + 10y = 200 в тождество. При желании на те же 200 рублей школьник может купить 4 пирожных и 10 чашек кофе:
В этом случае корнями уравнения 25x + 10y = 200 является пара значений (4; 10) .
Более того, школьник может вообще не покупать кофе, а купить пирожные на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 8 и 0
Или наоборот, не покупать пирожные, а купить кофе на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 0 и 20
Попробуем перечислить все возможные корни уравнения 25x + 10y = 200 . Условимся, что значения x и y принадлежат множеству целых чисел. И пусть эти значения будут бóльшими или равными нулю:
Так будет удобно и самому школьнику. Пирожные удобнее покупать целыми, чем к примеру несколько целых пирожных и половину пирожного. Кофе также удобнее брать целыми чашками, чем к примеру несколько целых чашек и половину чашки.
Заметим, что при нечетном x невозможно достичь равенства ни при каком y . Тогда значениями x будут следующие числа 0, 2, 4, 6, 8. А зная x можно без труда определить y
Таким образом, мы получили следующие пары значений (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Эти пары являются решениями или корнями уравнения 25x + 10y = 200 . Они обращают данное уравнение в тождество.
Уравнение вида ax + by = c называют линейным уравнением с двумя переменными. Решением или корнями этого уравнения называют пару значений ( x; y ), которая обращает его в тождество.
Отметим также, что если линейное уравнение с двумя переменными записано в виде ax + b y = c , то говорят, что оно записано в каноническом (нормальном) виде.
Некоторые линейные уравнения с двумя переменными могут быть приведены к каноническому виду.
Например, уравнение 2(16x + 3y − 4) = 2(12 + 8x − y) можно привести к виду ax + by = c . Раскроем скобки в обеих частях этого уравнения, получим 32x + 6y − 8 = 24 + 16x − 2y . Слагаемые, содержащие неизвестные сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой. Тогда получим 32x − 16x + 6y + 2y = 24 + 8 . Приведём подобные слагаемые в обеих частях, получим уравнение 16x + 8y = 32. Это уравнение приведено к виду ax + by = c и является каноническим.
Рассмотренное ранее уравнение 25x + 10y = 200 также является линейным уравнением с двумя переменными в каноническом виде . В этом уравнении параметры a , b и c равны значениям 25, 10 и 200 соответственно.
На самом деле уравнение ax + by = c имеет бесчисленное множество решений. Решая уравнение 25x + 10y = 200, мы искали его корни только на множестве целых чисел. В результате получили несколько пар значений, которые обращали данное уравнение в тождество. Но на множестве рациональных чисел уравнение 25x + 10y = 200 будет иметь бесчисленное множество решений.
Для получения новых пар значений, нужно взять произвольное значение для x , затем выразить y . К примеру, возьмем для переменной x значение 7. Тогда получим уравнение с одной переменной 25 × 7 + 10y = 200 в котором можно выразить y
Пусть x = 15 . Тогда уравнение 25x + 10y = 200 примет вид 25 × 15 + 10y = 200. Отсюда находим, что y = −17,5
Пусть x = −3 . Тогда уравнение 25x + 10y = 200 примет вид 25 × (−3) + 10y = 200. Отсюда находим, что y = 27,5
Видео:Решение систем уравнений методом подстановкиСкачать

Система двух линейных уравнений с двумя переменными
Для уравнения ax + by = c можно сколько угодно раз брать произвольные значение для x и находить значения для y . Отдельно взятое такое уравнение будет иметь бесчисленное множество решений.
Но бывает и так, что переменные x и y связаны не одним, а двумя уравнениями. В этом случае они образуют так называемую систему линейных уравнений с двумя переменными. Такая система уравнений может иметь одну пару значений (или по-другому: «одно решение»).
Может случиться и так, что система вовсе не имеет решений. Бесчисленное множество решений система линейных уравнений может иметь в редких и в исключительных случаях.
Два линейных уравнения образуют систему тогда, когда значения x и y входят в каждое из этих уравнений.
Вернемся к самому первому уравнению 25x + 10y = 200 . Одной из пар значений для этого уравнения была пара (6; 5) . Это случай, когда на 200 рублей можно можно было купить 6 пирожных и 5 чашек кофе.
Составим задачу так, чтобы пара (6; 5) стала единственным решением для уравнения 25x + 10y = 200 . Для этого составим ещё одно уравнение, которое связывало бы те же x пирожных и y чашечек кофе.
Поставим текст задачи следующим образом:
«Школьник купил на 200 рублей несколько пирожных и несколько чашек кофе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе купил школьник, если известно что количество пирожных на одну единицу больше количества чашек кофе?»
Первое уравнение у нас уже есть. Это уравнение 25x + 10y = 200 . Теперь составим уравнение к условию «количество пирожных на одну единицу больше количества чашек кофе» .
Количество пирожных это x , а количество чашек кофе это y . Можно записать эту фразу с помощью уравнения x − y = 1. Это уравнение будет означать, что разница между пирожными и кофе составляет 1.
Либо второе уравнение можно записать как x = y + 1 . Это уравнение означает, что количество пирожных на единицу больше, чем количество чашек кофе. Поэтому для получения равенства, к количеству чашек кофе прибавлена единица. Это легко можно понять, если воспользоваться моделью весов, которые мы рассматривали при изучении простейших задач:
Получили два уравнения: 25x + 10y = 200 и x = y + 1. Поскольку значения x и y , а именно 6 и 5 входят в каждое из этих уравнений , то вместе они образуют систему. Запишем эту систему. Если уравнения образуют систему, то они обрамляются знаком системы. Знак системы это фигурная скобка:
Давайте решим данную систему. Это позволит увидеть, как мы придём к значениям 6 и 5. Существует много методов решения таких систем. Рассмотрим наиболее популярные из них.
Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Метод подстановки
Название этого метода говорит само за себя. Суть его заключается в том, чтобы одно уравнение подставить в другое, предварительно выразив одну из переменных.
В нашей системе ничего выражать не нужно. Во втором уравнении x = y + 1 переменная x уже выражена. Эта переменная равна выражению y + 1 . Тогда можно подставить это выражение в первое уравнение вместо переменной x
После подстановки выражения y + 1 в первое уравнение вместо x , получим уравнение 25(y + 1) + 10y = 200 . Это линейное уравнение с одной переменной. Такое уравнение решить довольно просто:
Мы нашли значение переменной y . Теперь подставим это значение в одно из уравнений и найдём значение x . Для этого удобно использовать второе уравнение x = y + 1 . В него и подставим значение y
Значит пара (6; 5) является решением системы уравнений, как мы и задумывали. Выполняем проверку и убеждаемся, что пара (6; 5) удовлетворяет системе:
Пример 2. Решить методом подстановки следующую систему уравнений:
Подставим первое уравнение x = 2 + y во второе уравнение 3x − 2y = 9 . В первом уравнении переменная x равна выражению 2 + y . Это выражение и подставим во второе уравнение вместо x
Теперь найдём значение x . Для этого подставим значение y в первое уравнение x = 2 + y
Значит решением системы 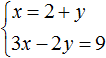
Пример 3. Решить методом подстановки следующую систему уравнений:
Здесь в отличие от предыдущих примеров, одна из переменных не выражена явно.
Чтобы подставить одно уравнение в другое, сначала нужно выразить одну из переменных.
Выражать желательно ту переменную, которая имеет коэффициент единицу. Коэффициент единицу имеет переменная x , которая содержится в первом уравнении x + 2y = 11 . Эту переменную и выразим.
После выражения переменной x , наша система примет следующий вид:
Теперь подставим первое уравнение во второе и найдем значение y
Подставим y в первое уравнение и найдём x
Значит решением системы 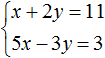
Конечно, выражать можно и переменную y . Корни от этого не изменятся. Но если выразить y, получится не очень-то и простое уравнение, на решение которого уйдет больше времени. Выглядеть это будет следующим образом:
Видим, что в данном примере выражать x намного удобнее, чем выражать y .
Пример 4. Решить методом подстановки следующую систему уравнений:
Выразим в первом уравнении x . Тогда система примет вид:
Подставим первое уравнение во второе и найдём y
Подставим y в первое уравнение и найдём x . Можно воспользоваться изначальным уравнением 7x + 9y = 8 , либо воспользоваться уравнением 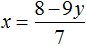
Значит решением системы 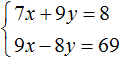
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Метод сложения
Метод сложения заключается в том, чтобы почленно сложить уравнения, входящие в систему. Это сложение приводит к тому, что образуется новое уравнение с одной переменной. А решить такое уравнение довольно просто.
Решим следующую систему уравнений:
Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. Получим следующее равенство:
Приведем подобные слагаемые:
В результате получили простейшее уравнение 3x = 27 корень которого равен 9. Зная значение x можно найти значение y . Подставим значение x во второе уравнение x − y = 3 . Получим 9 − y = 3 . Отсюда y = 6 .
Значит решением системы 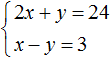
Пример 2. Решить следующую систему уравнений методом сложения:
Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. В получившемся равенстве приведем подобные слагаемые:
В результате получили простейшее уравнение 5 x = 20, корень которого равен 4. Зная значение x можно найти значение y . Подставим значение x в первое уравнение 2 x + y = 11 . Получим 8 + y = 11 . Отсюда y = 3 .
Значит решением системы 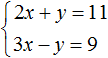
Процесс сложения подробно не расписывают. Его нужно выполнять в уме. При сложении оба уравнения должны быть приведены к каноническому виду. То есть к виду ax + by = c .
Из рассмотренных примеров видно, что основная цель сложения уравнений это избавление от одной из переменных. Но не всегда удаётся сразу решить систему уравнений методом сложения. Чаще всего систему предварительно приводят к виду, при котором можно сложить уравнения, входящие в эту систему.
Например, систему 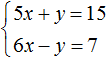
А систему уравнений 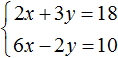
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Это правило справедливо и для системы линейных уравнений с двумя переменными. Одно из уравнений (или оба уравнения) можно умножить на какое-нибудь число. В результате получится равносильная система, корни которой будут совпадать с предыдущей.
Вернемся к самой первой системе 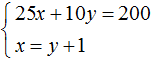
Умножим оба уравнения, входящие в эту систему на какие-нибудь числа. Скажем первое уравнение умножим на 2, а второе на 3
В результате получили систему 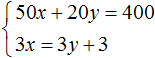
Решением этой системы по-прежнему является пара значений (6; 5)
Это значит, что уравнения входящие в систему можно привести к виду, пригодному для применения метода сложения.
Вернемся к системе 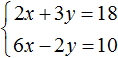
Умножим первое уравнение на 6, а второе на −2
Тогда получим следующую систему:
Сложим уравнения, входящие в эту систему. Сложение компонентов 12x и −12x даст в результате 0, сложение 18y и 4y даст 22y , а сложение 108 и −20 даст 88. Тогда получится уравнение 22y = 88 , отсюда y = 4 .
Если первое время тяжело складывать уравнения в уме, то можно записывать как складывается левая часть первого уравнения с левой частью второго уравнения, а правая часть первого уравнения с правой частью второго уравнения:
Зная, что значение переменной y равно 4, можно найти значение x. Подставим y в одно из уравнений, например в первое уравнение 2x + 3y = 18 . Тогда получим уравнение с одной переменной 2x + 12 = 18 . Перенесем 12 в правую часть, изменив знак, получим 2x = 6 , отсюда x = 3 .
Пример 4. Решить следующую систему уравнений методом сложения:
Умножим второе уравнение на −1. Тогда система примет следующий вид:
Сложим оба уравнения. Сложение компонентов x и −x даст в результате 0, сложение 5y и 3y даст 8y , а сложение 7 и 1 даст 8. В результате получится уравнение 8y = 8 , корень которого равен 1. Зная, что значение y равно 1, можно найти значение x .
Подставим y в первое уравнение, получим x + 5 = 7 , отсюда x = 2
Пример 5. Решить следующую систему уравнений методом сложения:
Желательно, чтобы слагаемые содержащие одинаковые переменные, располагались друг под другом. Поэтому во втором уравнении слагаемые 5y и −2x поменяем местами. В результате система примет вид:
Умножим второе уравнение на 3. Тогда система примет вид:
Теперь сложим оба уравнения. В результате сложения получим уравнение 8y = 16 , корень которого равен 2.
Подставим y в первое уравнение, получим 6x − 14 = 40 . Перенесем слагаемое −14 в правую часть, изменив знак, получим 6x = 54 . Отсюда x = 9.
Пример 6. Решить следующую систему уравнений методом сложения:
Избавимся от дробей. Умножим первое уравнение на 36, а второе на 12
В получившейся системе 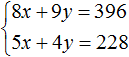
Сложим уравнения в получившейся системе. Тогда получим простейшее уравнение −13y = −156 . Отсюда y = 12 . Подставим y в первое уравнение и найдем x
Пример 7. Решить следующую систему уравнений методом сложения:
Приведем оба уравнения к нормальному виду. Здесь удобно применить правило пропорции в обоих уравнениях. Если в первом уравнении правую часть представить как 

У нас получилась пропорция. Перемножим её крайние и средние члены. Тогда система примет вид:
Первое уравнение умножим на −3, а во втором раскроем скобки:
Теперь сложим оба уравнения. В результате сложения этих уравнений, мы получим равенство, в обеих частях которого будет ноль:
Получается, что система 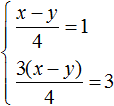
Но мы не можем просто так взять с неба произвольные значения для x и y . Мы можем указать одно из значений, а другое определится в зависимости от значения, указанного нами. Например, пусть x = 2 . Подставим это значение в систему:
В результате решения одного из уравнений, определится значение для y , которое будет удовлетворять обоим уравнениям:
Получившаяся пара значений (2; −2) будет удовлетворять системе:
Найдём еще одну пару значений. Пусть x = 4. Подставим это значение в систему:
На глаз можно определить, что значение y равно нулю. Тогда получим пару значений (4; 0), которая удовлетворяет нашей системе:
Пример 8. Решить следующую систему уравнений методом сложения:
Умножим первое уравнение на 6, а второе на 12
Перепишем то, что осталось:
Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:
Первое уравнение умножим на −1. Тогда система примет вид:
Теперь сложим оба уравнения. В результате сложения образуется уравнение 6b = 48 , корень которого равен 8. Подставим b в первое уравнение и найдём a
Видео:Теорема о количестве решений системы линейных уравненийСкачать

Система линейных уравнений с тремя переменными
В линейное уравнение с тремя переменными входит три переменные с коэффициентами, а также свободный член. В каноническом виде его можно записать следующим образом:
Данное уравнение имеет бесчисленное множество решений. Придавая двум переменным различные значения, можно найти третье значение. Решением в этом случае является тройка значений (x; y; z) которая обращает уравнение в тождество.
Если переменные x, y, z связаны между собой тремя уравнениями, то образуется система трех линейных уравнений с тремя переменными. Для решения такой системы можно применять те же методы, которые применяются к линейным уравнениям с двумя переменными: метод подстановки и метод сложения.
Пример 1. Решить следующую систему уравнений методом подстановки:
Выразим в третьем уравнении x . Тогда система примет вид:
Теперь выполним подстановку. Переменная x равна выражению 3 − 2y − 2z . Подставим это выражение в первое и второе уравнение:
Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:
Мы пришли к системе линейных уравнений с двумя переменными. В данном случае удобно применить метод сложения. В результате переменная y исчезнет, и мы сможем найти значение переменной z
Теперь найдём значение y . Для этого удобно воспользоваться уравнением −y + z = 4. Подставим в него значение z
Теперь найдём значение x . Для этого удобно воспользоваться уравнением x = 3 − 2y − 2z . Подставим в него значения y и z
Таким образом, тройка значений (3; −2; 2) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:
Пример 2. Решить систему методом сложения
Сложим первое уравнение со вторым, умноженным на −2.
Если второе уравнение умножить на −2, то оно примет вид −6x + 6y − 4z = −4 . Теперь сложим его с первым уравнением:
Видим, что в результате элементарных преобразований, определилось значение переменной x . Оно равно единице.
Вернемся к главной системе. Сложим второе уравнение с третьим, умноженным на −1. Если третье уравнение умножить на −1, то оно примет вид −4x + 5y − 2z = −1 . Теперь сложим его со вторым уравнением:
Получили уравнение x − 2y = −1 . Подставим в него значение x , которое мы находили ранее. Тогда мы сможем определить значение y
Теперь нам известны значения x и y . Это позволяет определить значение z . Воспользуемся одним из уравнений, входящим в систему:
Таким образом, тройка значений (1; 1; 1) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:
Видео:Исследование систем линейных уравнений на совместностьСкачать

Задачи на составление систем линейных уравнений
Задача на составление систем уравнений решается путем ввода нескольких переменных. Далее составляются уравнения на основании условий задачи. Из составленных уравнений образуют систему и решают её. Решив систему, необходимо выполнить проверку на то, удовлетворяет ли её решение условиям задачи.
Задача 1. Из города в колхоз выехала машина «Волга». Обратно она возвращалась по другой дороге, которая была на 5 км короче первой. Всего в оба конца машина проехала 35 км. Сколько километров составляет длина каждой дороги?
Решение
Пусть x — длина первой дороги, y — длина второй. Если в оба конца машина проехала 35 км, то первое уравнение можно записать как x + y = 35. Это уравнение описывает сумму длин обеих дорог.
Сказано, что обратно машина возвращалась по дороге которая была короче первой на 5 км. Тогда второе уравнение можно записать как x − y = 5. Это уравнение показывает, что разница между длинами дорог составляет 5 км.
Либо второе уравнение можно записать как x = y + 5 . Этим уравнением и воспользуемся.
Поскольку переменные x и y в обоих уравнениях обозначают одно и то же число, то мы можем образовать из них систему:
Решим эту систему каким-нибудь из изученных ранее методов. В данном случае удобно воспользоваться методом подстановки, поскольку во втором уравнении переменная x уже выражена.
Подставим второе уравнение в первое и найдём y
Подставим найденное значение y в во второе уравнение x = y + 5 и найдём x
Длина первой дороги была обозначена через переменную x . Теперь мы нашли её значение. Переменная x равна 20. Значит длина первой дороги составляет 20 км.
А длина второй дороги была обозначена через y . Значение этой переменной равно 15. Значит длина второй дороги составляет 15 км.
Выполним проверку. Для начала убедимся, что система решена правильно:
Теперь проверим удовлетворяет ли решение (20; 15) условиям задачи.
Было сказано, что всего в оба конца машина проехала 35 км. Складываем длины обеих дорог и убеждаемся, что решение (20; 15) удовлетворяет данному условию: 20 км + 15 км = 35 км
Следующее условие: обратно машина возвращалась по другой дороге, которая была на 5 км короче первой . Видим, что решение (20; 15) удовлетворяет и этому условию, поскольку 15 км короче, чем 20 км на 5 км: 20 км − 15 км = 5 км
При составлении системы важно, чтобы переменные обозначали одни и те же числа во всех уравнениях, входящих в эту систему.
Так наша система 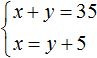
Задача 2. На платформу были погружены дубовые и сосновые шпалы, всего 300 шпал. Известно, что все дубовые шпалы весили на 1 т меньше, чем все сосновые. Определить, сколько было дубовых и сосновых шпал отдельно, если каждая дубовая шпала весила 46 кг, а каждая сосновая 28 кг.
Решение
Пусть x дубовых и y сосновых шпал было погружено на платформу. Если всего шпал было 300, то первое уравнение можно записать как x + y = 300 .
Все дубовые шпалы весили 46x кг, а сосновые весили 28y кг. Поскольку дубовые шпалы весили на 1 т меньше, чем сосновые, то второе уравнение можно записать, как 28y − 46x = 1000 . Это уравнение показывает, что разница масс между дубовыми и сосновыми шпалами, составляет 1000 кг.
В результате получаем два уравнения, которые образуют систему
Решим данную систему. Выразим в первом уравнении x . Тогда система примет вид:
Подставим первое уравнение во второе и найдём y
Подставим y в уравнение x = 300 − y и узнаем чему равно x
Значит на платформу было погружено 100 дубовых и 200 сосновых шпал.
Проверим удовлетворяет ли решение (100; 200) условиям задачи. Для начала убедимся, что система решена правильно:
Было сказано, что всего было 300 шпал. Складываем количество дубовых и сосновых шпал и убеждаемся, что решение (100; 200) удовлетворяет данному условию: 100 + 200 = 300.
Следующее условие: все дубовые шпалы весили на 1 т меньше, чем все сосновые . Видим, что решение (100; 200) удовлетворяет и этому условию, поскольку 46 × 100 кг дубовых шпал легче, чем 28 × 200 кг сосновых шпал: 5600 кг − 4600 кг = 1000 кг.
Задача 3. Взяли три куска сплава меди с никелем в отношениях 2 : 1 , 3 : 1 и 5 : 1 по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4 : 1 . Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго.
Решение
Пусть x — масса первого куска, y — масса второго куска, z — масса третьего куска. Если из этих кусков сплавлен кусок массой 12 кг, то первое уравнение можно записать как x + y + z = 12 .
Масса первого куска вдвое больше массы второго куска. Тогда второе уравнение можно записать как x = 2y .
Полученных двух уравнений недостаточно для решения данной задачи. Если второе уравнение подставить в первое, то мы получим уравнение 2y + y + z = 12 , откуда 3y + z = 12 . Это уравнение имеет бесчисленное множество решений.
Составим ещё одно уравнение. Пусть это уравнение будет описывать количество меди, взятого с каждого сплава и сколько меди оказалось в получившемся сплаве.
Если первый сплав имеет массу x , а медь и никель находится нём в отношении 2 : 1 , то можно записать, что в новом сплаве содержится 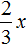
Если второй сплав имеет массу y , а медь и никель находится в нём в отношении 3 : 1 , то можно записать, что в новом сплаве содержится 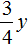
Если третий сплав имеет массу z , а медь и никель находится в отношении 5 : 1 , то можно записать, что в новом сплаве содержится 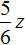
Полученный сплав имеет имеет массу 12 кг, а медь и никель находится в нём в отношении 4 : 1 . Тогда можно записать, что в полученном сплаве содержится 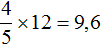
Сложим 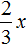
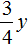
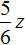
Попробуем решить данную систему.
Для начала упростим третье уравнение. Подставим в него второе уравнение и посмотрим, что из этого выйдет:
Теперь в главной системе вместо уравнения 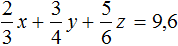
Подставим второе уравнение в первое:
Умножим первое уравнение на −10 . Тогда система примет вид:
Сложим оба уравнения. Тогда получим простейшее уравнение −5y = −4,8 откуда найдём y равный 0,96 . Значит масса второго сплава составляет 0,96 кг .
Теперь найдём x . Для этого удобно воспользоваться уравнением x = 2y. Значение y уже известно. Осталось только подставить его:
Значит масса первого сплава составляет 1,92 кг .
Теперь найдём z . Для этого удобно воспользоваться уравнением x + y + z = 12 . Значения x и y уже известны. Подставим их куда нужно:
Значит масса третьего сплава составляет 9,12 кг.
Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Системы линейных уравнений
Содержание:
Системы линейных уравнений. Понятия линейного уравнения и системы линейных уравнений
Напомним, что линейным уравнением с неизвестными 

Числа 
Определение 1. Систему алгебраических уравнений, каждое из которых имеет вид (1), называют системой линейных уравнений или линейной системой.
Система 




Коэффициенты уравнений нумеруют двумя индексами, первый из которых — номер уравнения, а второй — номер неизвестного.
Систему (2) удобно записывать в виде таблицы:
Решением системы (2) является любой набор значений неизвестных
удовлетворяющий всем уравнениям системы. Система, не имеющая ни одного решения, называется несовместной.
Две системы уравнений с одними и теми же неизвестными 
Для любой системы (2) возможны три случая:
1) система не имеет ни одного решения;
2) система имеет единственное решение;
3) система имеет бесконечное множество решений.
Множество всех решений системы (2) называют ее общим решением. Решить систему означает найти ее общее решение.
Над системой (2) можно совершать элементарные преобразования:
1) перестановка уравнений;
2) вычеркивание из системы уравнения вида
или, проще говоря, 0 = 0;
3) умножение обеих частей уравнения системы на число 
4) прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на одно и то же число.
Пример №15
Решить систему уравнений
Решение:
1) Если не выходить за рамки школьной математики, то можно в одном из уравнений выразить одно неизвестное через другое и подставить в оставшееся уравнение:
2) Если же использовать элементарные преобразования над системой, то можно ко второму уравнению, умноженному на 2, прибавить первое и, т.о., исключить из второго уравнения переменную 
Продолжая дальше заниматься теорией линейных систем, заметим, что при выполнении элементарных преобразований может возникнуть уравнение вида

где
Метод Гаусса решения систем линейных уравнений
Для нахождения общего решения линейных систем вида (2) имеется универсальный метод Гаусса — метода последовательного исключения неизвестных. Суть метода заключается в том, что с помощью элементарных преобразований системы (2) либо получают систему, содержащую противоречивое уравнение (и тогда система оказывается несовместной), либо система (2) приводится к некоторому специальному виду. Особенность этого вида заключается в том, что для каждого уравнения имеется неизвестное, которое входит в это уравнение с коэффициентом, не равным нулю, а в остальные уравнения — с коэффициентом 0. Если для каждого уравнения зафиксировано такое неизвестное, то оно называется базисным, а весь набор базисных неизвестных — базисом неизвестных. Остальные неизвестные (если они есть) называются свободными.
Пример №16
Рассмотрим систему линейных уравнений
Решение:
Здесь 

Перепишем нашу систему в виде:
Базисные переменные помещены в левых частях уравнений, свободные — в правых. В итоге получено общее решение системы. Подставляя вместо свободных неизвестных 




Замечание. При наличии хотя бы одного свободного неизвестного система имеет бесконечное множество решений. Если же свободных неизвестных нет (все неизвестные — базисные), то решение единственно.
Опишем алгоритм метода Гаусса.
Шаг первый. Одно из уравнений (например, первое) выбирается за разрешающее уравнение и одно из неизвестных (например, 
Шаг второй. Какое-то другое уравнение выбирается за разрешающее и одно из неизвестных в нем выбирается за разрешающее неизвестное. К этому выбору предъявляются два требования: 1) на предыдущих шагах это уравнение не было разрешающим; 2) в разрешающем уравнении коэффициент при разрешающем неизвестном должен быть отличен от нуля. Остальные действия такие же, как в шаге первом.
Процесс заканчивается, если ни одно из уравнений уже нельзя выбрать за разрешающее (т.е. все уравнения уже были в этой роли). Тогда для каждого уравнения имеется свое базисное неизвестное, входящее в это уравнение с коэффициентом, отличным от нуля, а в остальные уравнения — с коэффициентом 0. Т.о., процесс прекращается после получения базиса неизвестных. Т.е. мы нашли общее решение системы.
Пример №17
Найти общее решение системы линейных уравнений
Решение:
Последовательность действий будем записывать в виде таблиц. Разрешающие элементы отмечаются квадратными скобками. Конкретные действия комментируются в крайнем правом столбце таблицы. Например, запись *(-2)+ означает, что третье уравнение системы, умноженное на число (-2), прибавлено к первому уравнению.
Последней таблице соответствует система
Подстановкой в исходную систему убеждаемся в правильности решения.
Ответ: система имеет единственное решение 
Пример №18
Найти общее решение системы линейных уравнений
Решение:
Последней таблице соответствует система
Таким образом, 

Ответ: система имеет бесконечное множество решении 

Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
| Высшая математика: полный курс лекций |
Другие темы которые вам помогут понять высшую математику:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Видео:Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать

Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Видео:Матричный метод решения систем уравненийСкачать

Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:7 класс, 39 урок, Метод алгебраического сложенияСкачать

Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Видео:Система уравнений. Тема1 Система линейных уравнений.Скачать

Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Видео:СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Видео:Решение системы уравнений методом Крамера 2x2Скачать

Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Видео:Решение системы линейных уравнений с двумя переменными способом сложения. 6 класс.Скачать

Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
📽️ Видео
Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Алгебра 7. Урок 8 - Системы линейных уравненийСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Решение системы уравнений методом Крамера.Скачать

Решение системы уравнений методом ГауссаСкачать