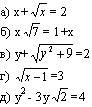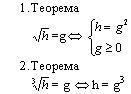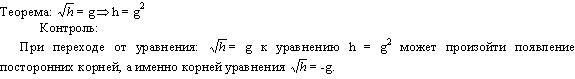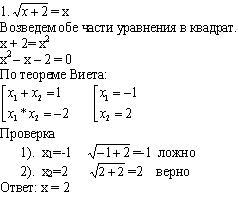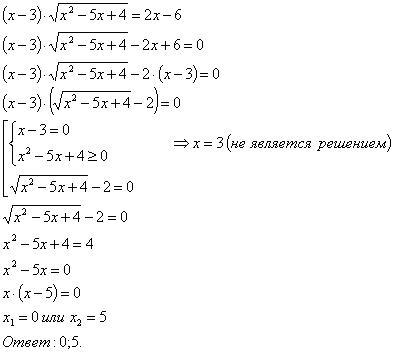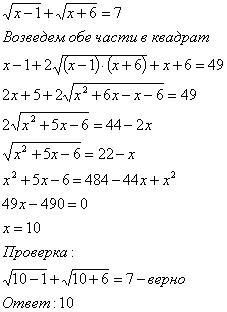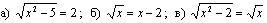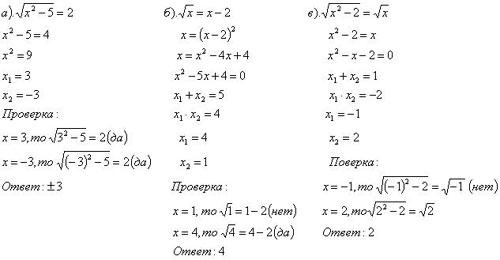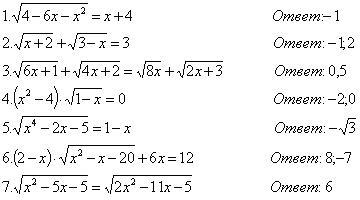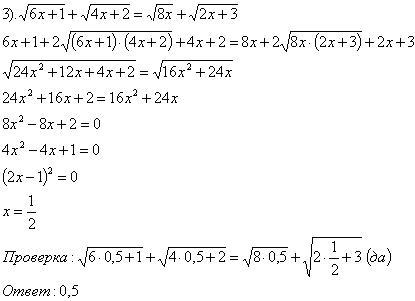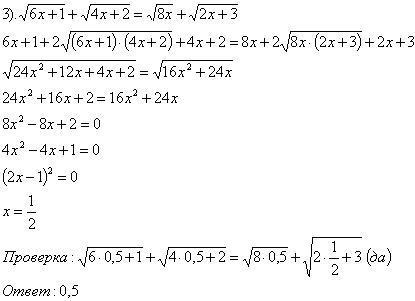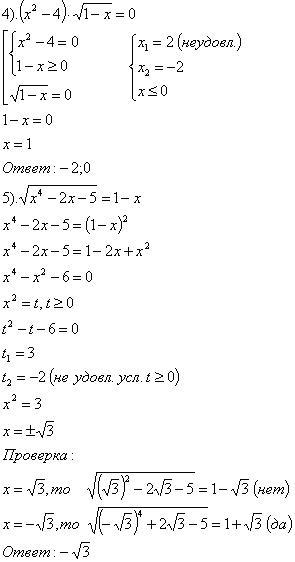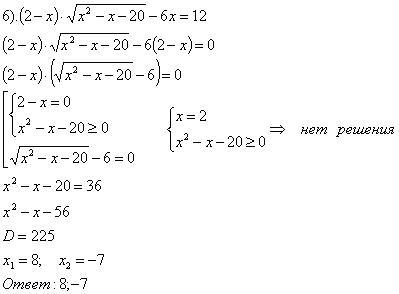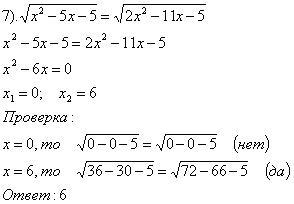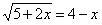ТЕМА: «Иррациональные уравнения»
Обучающая: Ввести понятие иррационального уравнения и показать способ решения через проверку корней способом подставки в исходное уравнение.
Развивающая: Способствовать развитию навыка решения иррациональных уравнений.
Воспитательная: Воспитывать навыки аккуратности и правильности оформления уравнения в тетрадях.
Ход урока
I. Организационный момент
II. Проверка домашнего задания
III. Устно (можно использовать доску, карточки, презентацию).
- Просмотр содержимого документа «Открытый урок по теме » Иррациональные уравнения». »
- Открытый урок по алгебре — тема » Решение иррациональных уравнений» для 10 класса методическая разработка по алгебре (10 класс) на тему
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Открытый урок «Иррациональные уравнения»
- Математика: теория и методика преподавания в образовательной организации
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 📸 Видео
Просмотр содержимого документа
«Открытый урок по теме » Иррациональные уравнения». »
Преподаватель математики: Берговина Ирина Анатольевна
АУ РС(Я) «Южно-Якутский технологический колледж» г. Нерюнгри
ТЕМА: «Иррациональные уравнения»
Обучающая: Ввести понятие иррационального уравнения и показать способ решения через проверку корней способом подставки в исходное уравнение.
Развивающая: Способствовать развитию навыка решения иррациональных уравнений.
Воспитательная: Воспитывать навыки аккуратности и правильности оформления уравнения в тетрадях.
I. Организационный момент
II. Проверка домашнего задания
III. Устно (можно использовать доску, карточки, презентацию).
Преобразуйте выражение (представьте в виде многочлена)
а) (а-5) 2 ; (а 2 +4в) 2 ; (2а-3) 2 ; (-х-7) 2
25х 2 +40х+4 = (5х+2) 2
4х 2 +1-2х = (2х-1) 2;
в) Решить уравнение
Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.
Какие из следующих уравнений являются иррациональными?
А сейчас самостоятельно изучаем теорию, решения иррациональных уравнений используя различную литературу и учебник. Для большей заинтересованности учащихся при наличии компьютерного класса можно использовать электронный учебник.
При решении иррациональных уравнений почти всегда необходимо избавиться от радикалов.
Один из возможных методов состоит в том, что корень из выражения с переменой переносится в одну из частей равенства, а все остальные выражения в другую (уединение радикала).
После уединения выполняется возведение в квадрат, в куб или в другую степень.
При решении уравнения переходим к уравнению-следствию, проверка должна входить в решение как обязательная часть.
Проверка может осуществляться различными способами:
Каждый из найденных корней уравнения-следствия подставить в исходное уравнение и проверить, является ли он корнем исходного уравнения.
“Вспомнить” все неравенства, которые надо было включать в систему, чтобы переходы были равносильными, и проверить выполняются ли для найденных “корней” эти неравенства.
(Проверить выполнение неравенства иногда бывает значительно проще, чем выполнение точного равенства).
Сегодня мы разбираем только уравнения первого способа.
IV. Переходим к записям в тетрадь
Число. Тема: Иррациональные уравнения.
У каждого на парте карточка с уравнениями:
Далее сильные учащихся разбирают решение более сложного уравнения по шаблону (или использовать компьютер):
Остальные самостоятельно решают уравнение (на доске и в тетрадях объясняет решение учитель):
Проверка усвоения учащимися материала на оценку “3” — ученики остаются на местах и решают уравнения (по выбору 2):
Проверка усвоения учащимися материала на оценку “4” и “5”: учащиеся решают за компьютером уравнения по выбору из предложенных уравнений. Компьютер проверяет (с записью в тетрадь) или на местах (проверка по шаблону).
Оценка “5” — решены 5,6 уравнения, если нет решения 5,6 уравнения, то оценка “4”.
V. ИТОГ По окончании урока каждый ученик получает оценку и соответствующие домашнее задание.
Для тех, кто усвоил материал на оценку “3”: № 417(а),№ 418(а), №419(а).
Для тех, кто усвоил материал на оценку “4”: 1). Решить уравнение:
2). № 417(в), № 422(в), № 425(б).
Для тех, кто усвоил материал на оценку “5”: 1). Решить уравнение:
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Открытый урок по алгебре — тема » Решение иррациональных уравнений» для 10 класса
методическая разработка по алгебре (10 класс) на тему
Открытый урок по алгебре — тема » Решение иррациональных уравнений» для 10 класса
Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Скачать:
| Вложение | Размер |
|---|---|
| statya_urok_irratsionalnye_uravneniya.docx | 23.92 КБ |
Видео:Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Предварительный просмотр:
Урок по алгебре и началам анализа в 10 классе
Тема урока: «Иррациональные уравнения
Учитель: Цейтлина Марина Иосифовна
Цель урока : Знакомство с иррациональными уравнениями, приемы их решения.
— образовательные – познакомить учащихся с иррациональными уравнениями и приемами их решения;
— развивающие: развитие умений учебно-познавательной деятельности (умение организации учебного труда, работа с учебником и другими источниками информации). Развитие культуры устной и письменной речи.
Тип урока: комбинированный урок (ознакомление учащихся с новым материалом и проведение первичного закрепления материала)
Педагогические технологии: педагогика сотрудничества (учитель – ученик)
Метод обучения: обучение в сотрудничестве «Учимся вместе». Во время обсуждения учителю можно задавать любые вопросы.
Учебник: «Алгебра и начала анализа», Ш.А. Алимов, Ю. М. Калягин и др., Москва, «Просвещение», 2010г.
Так как тема «Иррациональные уравнения» рассчитана на 2часа, то данный урок охватывает не все приемы решения иррациональных уравнений. Данный урок позволяет рассмотреть только некоторые из них.
1. Организационные моменты. Сообщение темы урока.
2. Проверка домашнего задания.
3. Устная работа.
4. Изучение нового материала.
5. Выполнение упражнений по теме урока.
6. Подведение итогов урока.
7. Домашнее задание.
Проверка готовности класса к уроку. Сообщение темы урока с последующей записью названия темы в тетрадь.
2. Проверка домашнего задания.
3. Устная работа.
Выполняются следующие устные упражнения:
а) Найдите значение выражения: ; .
в) Для каких значений переменных равенство верно:
4. Изучение нового материала.
1 ) Определение. Уравнение, содержащее неизвестное под знаком корня, называется иррациональным уравнением.
Примеры: = х + 1; и т.д.
2) Основная задача — решить уравнение. А что это значит? (Найти корни уравнения или установить, что их нет). А что такое корень уравнения? (Ответ).
Давайте рассмотрим несколько иррациональных уравнений.
Задания 4; 5 разобрать на доске.
В уравнении «4.» интервалы неотрицательности левой и правой части не имеют области пересечения. Следовательно, не решая уравнения можно сказать, что уравнение не имеет решения.
В уравнении «5.» областью допустимых значений является число, равное 1, и только оно может являться корнем данного уравнения. При подстановке этого значения в левую часть уравнения получаем 0, а это означает, что уравнение не имеет решения. Нахождение О.Д.З. намного упростило решение данного уравнения.
Вывод. Прежде чем решать уравнение, желательно, если это возможно, проверить надо ли решать это уравнение.
3) Решение иррациональных уравнений. Простейшие иррациональные уравнения.
Решение иррациональных уравнений основано на следующем свойстве: при возведении обеих частей уравнения в натуральную степень получается уравнение – следствие данного.
а) Решение уравнения вида:
, где а — некоторое число.
Если а ≥ 0, уравнение равносильно уравнению f(x) = . Мы говорили о желательности записи О.Д.З. Почему в данном случае ее можно не писать?
Рассмотрим уравнение: ; х – 2 = 4;
Решаем №151 (1, 3, 5) устно.
б) Уравнение, в правой части которого стоит функция.
В этом случае при условии g(x) ≥ 0 имеем право обе части уравнения возвести в квадрат.
Замечание. Если не пишем условия неотрицательности правой части, решение уравнения заканчиваем проверкой.
в) Уравнение, содержащее в левой и правой частях функции под знаком корня.
Это уравнения вида:
Решение этого уравнения равносильно решению системы:
Замечание. Можно решать уравнения возведением обеих частей в квадрат, с обязательной проверкой полученных решений.
г) Уравнение вида: + = a
Если а ≥ 0, то уравнение сводится к решению системы: .
Замечание. а) Иногда удобнее для вычислений уединить один из корней.
б) Возвести обе части уравнения в квадрат и сделать проверку
Полученное уравнение сужает О.Д.З.
5. Выполнение упражнений по теме урока.
6. Подведение итогов урока.
На сегодняшнем уроке мы познакомились с иррациональным уравнением и некоторыми методами решения иррационального уравнения.
Рефлексия: Занятие подходит к концу. Пожалуйста, поделитесь своими мыслями о сегодняшнем занятии (хотя бы одним предложением).
Вам для этого помогут слова:
— Я заметил, что…, и т.д.
7. Домашнее задание.
№ 151(1), 154(2,4), 155(4), 156(3)
Второй урок позволит рассмотреть оставшиеся нерассмотренные методы решения иррациональных уравнений. Такие уравнения приведены ниже.
д) Уравнение вида: = 0
Это возможно тогда и только тогда, когда хотя бы один из множителей равен нулю.
а) Приравнивая каждый из множителей к нулю, получаем значения неизвестного и делаем проверку.
б) Используем О.Д.З.: g(x) ≥ 0. Делаем проверку по О.Д.З.
е) Использование свойств монотонности функции при решении иррациональных уравнений.
Рассмотрим это на примере решения уравнения
Пусть и у = 2, т.е. рассмотрим правую и левую части уравнений как функции переменной х f(x) и g(x) соответственно. Тогда f(x) является монотонно возрастающей для всех х ≥ 1, а g(x) = const. Используем утверждение, что, если одна из функций возрастающая (убывающая), другая – убывающая (возрастающая) или является постоянной, то уравнение имеет не более одного корня. В нашем случае х = 1.
ж) Решение иррациональных уравнений с помощью введения вспомогательной переменной.
Рассматриваем на примере:
Делаем следующую замену:
Тогда уравнение принимает вид: , а далее решение этого уравнения см.в разделе б).
З) Решение иррациональных уравнений с помощью разложения на множители.
Рассматриваем на примере:
Каждое подкоренное выражение содержит общий множитель х-1, тогда, перенеся все члены уравнения в одну сторону, можно общий множитель вынести за скобку и решать уравнение одним из рассмотренных ранее способов.
Видео:Иррациональные уравнения. Видеоурок 8. Алгебра 10 классСкачать

По теме: методические разработки, презентации и конспекты
Презентация к уроку математики по теме «Решение уравнений» ( 5 класс)
Презентация по теме «Решение уравнений» ( 5 класс) подготовлена к уроку обьяснения решения усложнённых уравнений на основании зависимостей между компонентами и свойств арифметических.
Открытый урок -семинар по теме «Решение тригонометрических уравнений» в 10 классе
Отработать навыки решения тригонометрических уравнений, приводимых к квадратным, и однородных уравнений.
Открытый урок по алгебре и началам в 10 классе « ЕГЭ на «5»!» (Интерактивные технологии с применением ИКТ, обобщающий урок повторения по теме «Тригонометрические преобразования, уравнения и неравенства»)
Задача урока: Развивая, обучать и воспитывать.Обучающая цель: Привести в систему знания, полученные по данной теме, тем самым подготовить учащихся к сдаче выпускного и вступительного экзамена по матем.
Разработка открытого урока по алгебре и началам анализа (11 класс) на тему «Логарифмы и их свойства»)
Открытый урок представлен в игровой форме.
Урок-семинар по теме «Решение иррациональных уравнений»
обобщение знаний и способов решения иррациональных уравнений;знакомство с нестандартными методами решения иррациональных уравнений.
Открытый урок по алгебре «Логарифмические уравнения» в 11 класса
цель урока: формировать умение решать логарифмические уравнения, умение применять основные методы решения и выбирать нужный способ.Развивать логическое мышление, математическую речь, умение срав.
Разработка урока по алгебре. Тема: решение текстовых задач
План-коспект урока по теме «Решение текстовых задач»( алгебра 8 класс по учебнику Макарычева Ю.Н). Прилагается презентация.
Видео:Иррациональные уравнения | Математика ЕГЭ 10 класс | УмскулСкачать

Открытый урок «Иррациональные уравнения»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Конспект открытого урока по алгебре и начала анализа в 10 классе.
Учебник : Алгебра и начала анализа за 10-11 класс .- авторы Алимов , Колягин, Ткачева, Федорова, Шабунин , 2015 год ФГОС.
Дата проведения открытого урока: 10.112020
ТЕМА: «Иррациональные уравнения»
Обучающая: дать понятие иррационального уравнения и рассмотреть способ решения.
Развивающая: Способствовать развитию навыка решения иррациональных уравнений.
Воспитательная: Воспитывать навыки аккуратности и правильности оформления уравнения в тетрадях.
I. Организационный момент
II. Проверка домашнего задания
III. Устно (можно использовать доску, карточки, презентацию).
Преобразуйте выражение (представьте в виде многочлена)
а) (а-5) 2 ; (а 2 +4в) 2 ; (2а-3) 2 ; (-х-7) 2
25х 2 +40х+4 = (5х+2) 2
4х 2 +1-2х = (2х-1) 2;
в) Решить уравнение
Опр .Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.
Какие из следующих уравнений являются иррациональными?
Рассмотрим общий способ решения
При решении иррациональных уравнений почти всегда необходимо избавиться от радикалов.
Один из возможных методов состоит в том, что корень из выражения с переменой переносится в одну из частей равенства, а все остальные выражения в другую (уединение радикала).
После уединения выполняется возведение в квадрат, в куб или в другую степень.
При решении уравнения переходим к уравнению-следствию, проверка должна входить в решение как обязательная часть.
Проверка может осуществляться различными способами:
Каждый из найденных корней уравнения-следствия подставить в исходное уравнение и проверить, является ли он корнем исходного уравнения.
“ Вспомнить” все неравенства, которые надо было включать в систему, чтобы переходы были равносильными, и проверить выполняются ли для найденных “корней” эти неравенства.
(Проверить выполнение неравенства иногда бывает значительно проще, чем выполнение точного равенства).
Сегодня мы разбираем только уравнения первого способа.
IV. Переходим к записям в тетрадь
Число. Тема: Иррациональные уравнения.
У каждого на парте карточка с уравнениями:
Далее сильные учащихся разбирают решение более сложного уравнения по шаблону
Остальные самостоятельно решают уравнение (на доске и в тетрадях объясняет решение учитель):
Проверка усвоения учащимися материала на оценку “3” — ученики остаются на местах и решают уравнения (по выбору 2):
Проверка усвоения учащимися материала на оценку “4” и “5”: учащиеся решают уравнения по выбору из предложенных уравнений..
Оценка “5” — решены 5,6 уравнения, если нет решения 5,6 уравнения, то оценка “4”.
V. Итоги и рефлексия. По окончании урока каждый ученик получает оценку и соответствующие домашнее задание.
Итак, ребята! Какие уравнения мы сегодня на уроке рассмотрели?
– Дать определение иррациональных уравнений.
– Какая особенность существует при решении иррациональных уравнений?
– Какие способы решения иррациональных уравнений мы рассмотрели ?
Домашнее задание : №152(2,3), 154(2,4), 155(2)
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 691 человек из 75 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 861 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 51 человек из 23 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:Иррациональные уравнения за 45 минут | Математика 10 класс | УмскулСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 841 597 материалов в базе
Материал подходит для УМК
«Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
§ 9. Иррациональные уравнения
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 19.11.2020
- 77
- 2
- 19.11.2020
- 94
- 3
- 19.11.2020
- 411
- 12
- 19.11.2020
- 103
- 3
- 19.11.2020
- 138
- 0
- 19.11.2020
- 106
- 1
- 19.11.2020
- 125
- 0
- 19.11.2020
- 114
- 0
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 19.11.2020 1041
- DOCX 262.3 кбайт
- 169 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Лаврентьев Александр Владимирович. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 5 месяцев
- Подписчики: 0
- Всего просмотров: 1076
- Всего материалов: 1
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Иррациональные уравнения — часть 1Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Вузы РФ не будут повышать стоимость обучения на первом курсе
Время чтения: 1 минута
Госдума рассматривает проект о регулировании «продленок» в школах
Время чтения: 1 минута
Онлайн-конференция о профессиональном имидже педагога
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📸 Видео
Иррациональные уравнения | Математика ЕГЭ 10 класс | УмскулСкачать

Иррациональные уравнения и их системы. 11 класс.Скачать

Иррациональные уравнения. Практика. Видеоурок 8. Алгебра 10 классСкачать

8 класс, 38 урок, Иррациональные уравненияСкачать

Иррациональные неравенства | Математика ЕГЭ 10 класс | УмскулСкачать

Открытый урок в 10 классе "Иррациональные уравнения"Скачать

Иррациональные уравнения и их системы. Практическая часть. 1ч. 11 класс.Скачать

Иррациональные уравнения. 10 классСкачать

Простейшие иррациональные уравнения. Иррациональные уравнения Часть 1 из 2Скачать

Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Иррациональные уравнения. 10 класс.Скачать

Иррациональные неравенства | Математика ЕГЭ | УмскулСкачать

Все об иррациональных уравнениях №13 | Математика ЕГЭ для 10 класса | УмскулСкачать