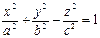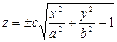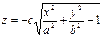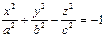Практическая работа
Цель работы: Научиться решать в MS Excel задачи.
• Задание 1. Вычислить следующие математические функции:
у1 = sin2x; у2 = 2 sin х; у3 = sin(x + 2), при х ϵ [-3; 3], шаг = 0,5;
у1 = cos х; у2= 2cos х, при х ϵ [-3; 3] шаг= 0,5;
у1 = tgx; у2 = ctgx, при хϵ [0,5; 7], шаг = 0,5;
у1 = 1/х; у2= 
,при х ϵ [0;9], шаг = 1.
Результат работы представить в виде таблицы и построить графики функций.
Порядок выполнения задания
1. Откройте Лист 7 в файле «Книга 1».
2. Вычислите математические функции, все расчеты представьте в виде таблиц и постройте графики, как описано в Заданиях 2 и 3 практической работы в предыдущем параграфе.
3.Постройте график функции y = x 3 + x 2 – x + 4 на отрезке [-3;3] с шагом 0,5. Проанализируйте график функции, найдите промежутки ее возрастания и убывания, экстремумы и точки пересечения с осями координат. Запишите результаты анализа под таблицей.
4.Решите графически уравнение 2x 3 + 3x 2 + 5 = 0 аналогично второму примеру и запишите результат решения под таблицей.
Таблица 2.9
| х | у=х 3 +х 2 -х+4 |
| -3 | -11 |
| -2,6 | -4,216 |
| -2,2 | 0,392 |
| -1,8 | 3,208 |
| -1,4 | 4,616 |
| -1 | |
| -0,6 | 4,744 |
| -0,2 | 4,232 |
| 0,2 | 3,848 |
| 0,6 | 3,976 |
| 1,4 | 7,304 |
| 1,8 | 11,272 |
| 2,2 | 17,288 |
| 2,6 | 25,736 |
Рис. 2.14
5. Присвойте Листу 7 имя «Графики 2» и сохраните в файле под именем «Книга 1».
Построение поверхностей
Практическая работа 1
Цель работы: Научиться строить поверхности.
Порядок выполнения работы
1. Откройте файл «Книга 1». На Листе 8 постройте поверхность, представляемую уравнением:
2. Для построения этой поверхности решите заданное уравнение относительно z с двумя аргументами х и у:
3. Для вычисления двух математических функций с двумя переменными создайте две таблицы по формулам:
Z = (х 2 + у 2 ) и Z = — (х 2 + у 2 ).
Первая функция представит поверхность в положительной полуплоскости, а вторая — в отрицательной.
Пусть х ϵ [-3; 3] и у ϵ [-3; 3], шаг = 0,5.
Формула для вычисления первой функции z= (х 2 +у 2 ) (табл. 2.10).
4. Обозначьте границы таблицы по образцу, выделяя необходимое количество столбцов и строк. Столбец и строку аргументов х и у заполните, используя функцию Автозаполнение.
5. Впишите формулу = ($А2 ^ 2+В$1 ^ 2) в ячейку В2 и нажмите клавишу Enter, Результат отобразится в ячейке В2.
Примечание. Для вычисления значений функции Z от двух переменных z = (х 2 + у 2 ) при перемещении по строке адрес ячейки, содержащей значение X, является абсолютным ($А2), меняется же адрес ячейки, содержащей значение У, который является в данном случае относительным. При перемещении же по столбцу адрес ячейки, содержащей значение У, является абсолютным (В$1), при этом меняется адрес ячейки, содержащей значение X, который является в данном случае относительным. Алгоритм вычисления функции Z задается формулой =($А2 ^ 2+В$1 ^ 2).
6. Выделите ячейку В2, потяните за правый нижний угол по строкам и столбцам и произведите вычисления по всей таблице.
Таблица 2.10
| х/у | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0,5 | 1,5 | 2,5 | ||||
| -3 | 15,3 | 11,3 | 9,25 | 9,25 | 11,3 | 15,3 | |||||||
| -2,5 | 15,25 | 12,5 | 10,3 | 8,5 | 7,25 | 6,5 | 6,25 | 6,5 | 7,25 | 8,5 | 10,3 | 12,5 | 15,3 |
| -2 | 10,3 | 6,25 | 4,25 | 4,25 | 6,25 | 10,3 | |||||||
| -1,5 | 11,25 | 8,5 | 6,25 | 4,5 | 3,25 | 2,5 | 2,25 | 2,5 | 3,25 | 4,5 | 6,25 | 8,5 | 11,3 |
| -1 | 7,25 | 3,25 | 1,25 | 1,25 | 3,25 | 7,25 | |||||||
| -0,5 | 9,25 | 6,5 | 4,25 | 2,5 | 1,25 | 0,5 | 0,25 | 0,5 | 1,25 | 2,5 | 4,25 | 6,5 | 9,25 |
| 6,25 | 2,25 | 0,25 | 0,25 | 2,25 | 6,25 | ||||||||
| 0,5 | 9,25 | 6,5 | 4,25 | 2,5 | 1,25 | 0,5 | 0,25 | 0,5 | 1,25 | 2,5 | 4,25 | 6,5 | 9,25 |
| 7,25 | 3,25 | 1,25 | 1,25 | 3,25 | 7,25 | ||||||||
| 1,5 | 11,25 | 8,5 | 6,25 | 4,5 | 3,25 | 2,5 | 2,25 | 2,5 | 3,25 | 4,5 | 6,25 | 8,5 | 11,3 |
| 10,3 | 6,25 | 4,25 | 4,25 | 6,25 | 10,3 | ||||||||
| 2,5 | 15,25 | 12,5 | 10,3 | 8,5 | 7,25 | 6,25 | 6,25 | 6,25 | 7,25 | 8,5 | 10,3 | 12,5 | 15,3 |
| 15,3 | 11,3 | 9,25 | 9,25 | 11,3 | 15,3 |
7. Для построенияграфика поверхности выделите таблицу, не включая строку и столбец со значениями x и y, выберите вкладку Вставка • Диаграммы • Другие диаграммы • Поверхность.
8. При помощи вкладки Работа с диаграммами оформите поверхность в соответствии с рис. 2.15
Рис. 2.15
9. Формула для вычисления второй функции z = — (х 2 + у 2 ).
10. Впишите формулу = — ($А2 ^ 2 + В$1^2) в ячейку В2 и нажмите клавишуEnter.Результат отобразится в ячейке В2 (табл. 2.11).
11. Далее продолжите выполнение задания в соответствии с п. 7, 8, 9.
Таблица 2.11
| х/у | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0,5 | 1,5 | 2,5 | ||||
| -3 | -18 | -15,3 | -13 | -11 | -10 | -9,25 | -9 | -9,25 | -10 | -11,3 | -13 | -15 | -18 |
| -2,5 | -15,3 | -12,5 | -10 | -8,5 | -7,25 | -6,5 | -6,25 | -6,5 | -7,25 | -8,5 | -10,3 | -13 | -15,3 |
| -2 | -13 | -10,3 | -8 | -6,3 | -5 | -4,25 | -4 | -4,25 | -5 | -6,25 | -8 | -10 | -13 |
| -1,5 | -11,3 | -8,5 | -6,3 | -4,5 | -3,25 | -2,5 | -2,25 | -2,5 | -3,25 | -4,5 | -6,25 | -8,5 | -11,3 |
| -1 | -10 | -7,25 | -5 | -3,3 | -2 | -1,25 | -1 | -1,25 | -2 | -3,25 | -5 | -7,3 | -10 |
| -0,5 | -9,25 | -6,5 | -4,3 | -2,5 | -1,25 | -0,5 | -0,25 | -0,5 | -1,25 | -2,5 | -4,25 | -6,5 | -9,25 |
| -9 | -6,25 | -4 | -2,3 | -1 | -0,25 | -0 | -0,25 | -1 | -2,25 | -4 | -6,3 | -9 | |
| 0,5 | -9,25 | -6,5 | -4,3 | -2,5 | -1,25 | -0,5 | -0,25 | -0,5 | -1,25 | -2,5 | -4,25 | -6,5 | -9,25 |
| -10 | -7,25 | -5 | -3,3 | -2 | -1,25 | -1 | -1,25 | -2 | -3,25 | -5 | -7,3 | -10 | |
| 1,5 | -11,3 | -8,5 | -6,3 | -4,5 | -3,25 | -2,5 | -2,25 | -2,5 | -3,25 | -4,5 | -6,25 | -8,5 | -11,3 |
| -13 | -10,3 | -8 | -6,3 | -5 | -4,25 | -4 | -4,25 | -5 | -6,25 | -8 | -10 | -13 | |
| 2,5 | -15,3 | -12,5 | -10 | -8,5 | -7,25 | -6,25 | -6,25 | -6,25 | -7,25 | -8,5 | -10,3 | -13 | -15,3 |
| -18 | -15,3 | -13 | -11 | -10 | -9,25 | -9 | -9,25 | -10 | -11,3 | -13 | -15 | -18 |
Рис. 2.16
Практическая работа 2
Цель работы: Самостоятельно построить поверхность, представляемую уравнением z = ± (х 2 — у 2 ).
Порядок выполнения работы
1. Уравнения для вычисления значений функции будут иметь следующий вид:
2. Задание выполните в соответствии с Практической работой 1.
3. В результате должны получиться табл. 2.12, 2.13 и графики поверхностей рис. 2.17, рис. 2.18.
- Практическая работа по теме «Использование программы Excel для решения математических задач»
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Информатика: теория и методика преподавания в образовательной организации
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Постройте однополостный гиперболоид
- 📹 Видео
Видео:СДНФ и СКНФ Табличный способСкачать
Практическая работа по теме «Использование программы Excel для решения математических задач»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
по теме «Использование программы Excel для решения математических задач »
ЦЕЛЬ: отработать навыки использования математических функций для решения прикладных задач, построения графиков функций.
Использование математических функций
На Листе 1 вычислите значения выражений, результаты оформите в виде таблицы:
На Листе2 вычислить :
Построение графиков функций
На Листе3 вычислите значения функций на отрезке и постройте графики функций как показано на рисунках:
Рис. 1 : при x [-3;3], шаг = 0,5
Рис. 2: при x [-7;5], шаг = 1
Рис. 3 : при x [-3;3], шаг = 0,5
Рис. 4: при x [-5;5], шаг = 0,5
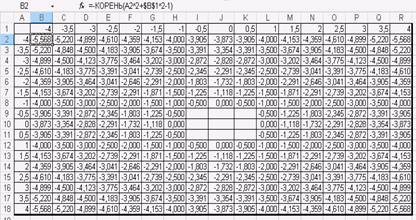
На Листе4 постройте поверхность, однополостный гиперболоид и задается уравнением:
Решаем заданное уравнение относительно z , получим 
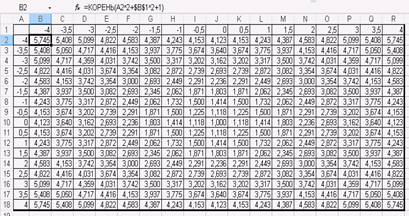
Создаем две таблицы для вычисления двух математических функций с двумя переменными: первая представит однополостный гиперболоид в положительной плоскости, вторая – в отрицательной.
Пусть x [-4;4] и y [-4;4]. Для упрощения формулы a = b = c =1. Для первой функции получим следующую таблицу:
Скопируйте формулу для всех значений. Аналогично постройте таблицу для второй функции.
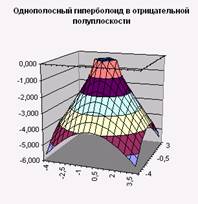
Постройте поверхности, выбрав диаграмму «Поверхность»:
Самостоятельно выполните следующие задания:
На Листе5 постройте поверхность, заданную уравнением
, при значении a =2, b =1, c =10. Значение коэффициентов задайте в отдельных ячейках (скопируйте ранее созданный таблицы и внесите изменения в формулы.
На Листе4 постройте поверхность, представляемую уравнением z = x 2 — y 2 , при x , y [-1;1], x изменяется с шагом 0,25, y изменяется с шагом 0,5.
Работа с матрицами
выбираем пустую ячейку, и находим значение первого элемента результирующей матрицы (суммируем первые элементы матриц);
за правый нижний угол растягиваем исходную ячейку в размер складываемых матриц и получаем сумму двух матриц.
выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы (предварительно необходимо определить размер диапазона).
в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;
на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .
после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Аналогично можно найти определитель матрицы и обратную матрицу , воспользовавшись функциями МОПРЕД и МОБР .
На Листе 6 выполните необходимые вычисления. Исходные данные оформите синим цветом символов, результат – красным.
Вычислите определитель и найдите обратную матрицу:
Найдите сумму матриц A и B :
Найдите произведение матриц A и B :
Краткое описание документа:
Предлагаю Вашему вниманию разработку практической работы «Использование программы Excel для решения математических задач». Материал содержит задания, направленные на отработку навыков использования инструментов табличного процессора MS Excel 2007 для решения различных математических задач: математические вычисления с использованием функций, построение графиков и поверхностей, работа с матрицами. Работа содержит как задания с пояснениями, так и задания, рассчитанные на самостоятельное выполнение. Работа может быть использована как в старших классах школы, так и для студентов СУЗов при изучении специальных дисциплин.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 864 человека из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 48 человек из 23 регионов
Курс профессиональной переподготовки
Информатика: теория и методика преподавания в образовательной организации
- Сейчас обучается 223 человека из 62 регионов
«Профессиональный имидж педагога: стереотипы и методы их преодоления»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
Видео:A.2.15 Построение совершенных дизъюнктивной и конъюнктивной нормальных форм (СДНФ и СКНФ)Скачать
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 838 778 материалов в базе
Ищем педагогов в команду «Инфоурок»
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 22.04.2014
- 2644
- 11
- 22.04.2014
- 1563
- 0
- 22.04.2014
- 2398
- 9
- 22.04.2014
- 2015
- 0
- 22.04.2014
- 8543
- 7
- 22.04.2014
- 4875
- 1
- 22.04.2014
- 966
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 22.04.2014 2781
- DOCX 605.7 кбайт
- 26 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Белоусова Ольга Леонидовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 9 месяцев
- Подписчики: 0
- Всего просмотров: 2037
- Всего материалов: 1
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:7 класс. Задачи на измерение информацииСкачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
Госдума рассматривает проект о регулировании «продленок» в школах
Время чтения: 1 минута
Около 20% детей до 15 лет не воспринимают прочитанную информацию
Время чтения: 1 минута
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
«Единая Россия» внесла в Госдуму проект о снятии излишней нагрузки с учителей
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Задание 11 | ЕГЭ по информатике | ДЕМО-2022Скачать
Постройте однополостный гиперболоид
Microsoft Excel
Задание 1. Постройте однополостный гиперболоид
1. Откройте файл под именем «Книга 1». На Листе 1 постройте поверхность, представляемую уравнением:
Такая поверхность называется однополосный гиперболоид.
2. Для построения этой поверхности решите заданное уравнение относительно z
3. Вам предстоит создать две таблицы для вычисления двух математических функций с двумя переменными
и 
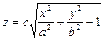
Первая функция представит однополосный гиперболоид в положительной полуплоскости, а вторая – в отрицательной.
Пусть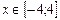 
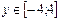
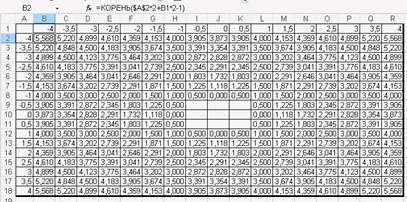
и 
. Для упрощения формул примите: a = b = c =1.
4. В таблице для вычисления первой функции (рис. 1) приведена формула, которую следует копировать по строкам и столбцам
 |
5. Аналогично будет выглядеть формула для вычисления второй функции. (См. рис. 2)
6. Постройте поверхности, выбрав диаграмму под названием «Поверхность» (Рис. 3, Рис. 4).
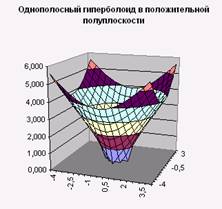
Задание 2. Постройте двуполостный гиперболоид
На Листе 3 постройте поверхность, представляемую уравнением
Такая поверхность называется двуполостный гиперболоид.
В таблице для вычисления первой функции (Рис. 5) приведена формула, которую следует скопировать по строкам и столбцам.
Аналогично будет выглядеть формула для вычислений второй функции. (См. рис. 6)
📹 Видео
Задача на КПД усложненная, физика 7 классСкачать
Оценка количественных параметров текстовых документов | Информатика 7 класс #28 | ИнфоурокСкачать
ДМ y2021-1к-л7 Коды, префиксные коды, неравенство Крафта-Мак Миллана, алгоритм ХаффманаСкачать
1 7 Формы представления переключательных функцийСкачать
Приведение булевой функции к ДНФСкачать
Дискретный анализ 7. Системы общих представителей 2Скачать
5. ФНП. Применение полного дифференциала к приближенным вычислениямСкачать
[EN] KB 001682 | Определение полезной длины крестообразных связей в RFEM 6Скачать
![[EN] KB 001682 | Определение полезной длины крестообразных связей в RFEM 6](https://i.ytimg.com/vi/EftMh9NV2mo/0.jpg)
ДНФ И КНФ Часть 1Скачать
ТФКП. Найти действительную и мнимую части функции комплексного переменного.Скачать
ДНФСкачать
Программирование в УТ 11.4. Взаимодействие с динамическими списками.Скачать
Как получить данные на форму из модуля объектаСкачать
Дискретный анализ 7. Системы общих представителейСкачать
Построение СДНФ и СКНФ по таблице истинностиСкачать
Урок 7. Функция ЕСЛИСкачать
