Отделите корни заданного уравнения пользуясь графическим методом схематически на бумаге

Пример 2.1. Отделить корни уравнения sin5x + x 2 – 1 = 0.

Решение. Построим таблицу значений функции y = sin5x + x 2 – 1 на отрезке [–4; 4] с шагом изменения аргумента h = 1, пользуясь калькулятором или электронными таблицами (табл. 2.1).

Табл. 2.1 показывает, что данное уравнение имеет корни в интервалах
(–1; 0) и (1; 2), так как функция меняет знак в этих промежутках. Пока мы не можем утверждать, что в найденных интервалах содержится ровно по одному корню и, что в других интервалах корней нет. Чтобы уточнить информацию о числе корней можно построить таблицу значений функции с меньшим шагом, например h = 0,1.

Для отделения корней уравнения естественно применять графический метод. График функции y = f(x) с учетом свойств функции дает много информации для определения числа корней уравнения f(x) = 0.

Построим для примера 2.1 график функции в программе Excel на отрезке [–1, 2] с шагом изменения аргумента h = 0,1. Для этого выполним следующие действия в программе Excel:

1) В диапазоне A2:A32 введем значения переменной x. Для этого в ячейке A2 запишем –1, в ячейке A3 — значение –1,9. После этого выделим диапазон A2:A3 и с помощью маркера заполнения присвоим значения остальным ячейкам до ячейки A32.

2) В ячейку B2 введем формулу =SIN(5*A2)+A2^2–1 и скопируем B2 с помощью маркера заполнения в остальные ячейки до ячейки B32.

3) Выделим диапазон A2:B32 и с помощью мастера диаграмм (тип диаграммы «Точечная, точечная диаграмма со значениями, соединенными отрезками без маркеров») построим график функции.

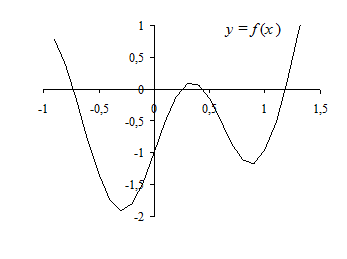
Полученный график представлен на рис. 2.1.

Из графика видно, что на отрезке [0; 0,5] есть два корня. Из таблицы A2:B32 значений функции заключаем, что уравнение имеет четыре корня в интервалах [–0,8; –0,7], [0,2; 0,3], [0,4; 0,5], [1,1; 1,2].

Чтобы убедиться в том, что больше корней нет, преобразуем уравнение к виду sin 5x = 1 – x 2 и построим графики двух функций f₁(x) = sin 5x и
f₂(x) = 1 – x 2 . Корням соответствуют абсциссы точек пересечения этих графиков. Так как значения первой функции ограничены и принадлежат отрезку [–1; 1], то подберем отрезок значений x для построения графиков так, чтобы за пределами этого отрезка значения второй функции были по абсолютной величине больше единицы. Искомые корни могут находиться только внутри этого отрезка. Очевидно, что отрезок [–2; 2] удовлетворяет этим условиям, так как при |x| > 2 выполнено неравенство |f₂(x)| > 1. Построим графики этих функций на отрезке [–2; 2] с шагом h = 0,2. Для этого в программе Excel выполним следующие действия:

1) В ячейке A2 запишем –2, в ячейке A3 значение –1,8. Выделим диапазон A2:A3 и с помощью маркера заполнения присвоим значения остальным ячейкам до появления значения 2 (до ячейки A42).

2) В ячейку B2 введем формулу =SIN(5*A2) и скопируем B2 с помощью маркера заполнения в остальные ячейки до ячейки B42.В ячейку C2 введем формулу =1–A2^2 и скопируем C2 с помощью маркера заполнения в остальные ячейки до ячейки C42.

3) Выделим диапазон A2:C42 и с помощью мастера диаграмм (тип диаграммы «Точечная») построим графики функций.

Из рис. 2.2 видно, что графики пересекаются в четырех точках и данное уравнение имеет ровно четыре корня, что подтверждает предыдущие выводы.

До настоящего времени графический метод предлагалось применять для нахождения грубого значения корня или нахождения интервала, содержащего корень, и затем применять итерационные методы, т.е. методы пос­­ледовательных приближений для уточнения значения корня. С появлением математических пакетов и электронных таблиц стало возможным вычислять таблицы значений функции с любым шагом и строить графики с высокой точностью. Это позволяет уточнять очередной знак в приближенном значении корня при помощи следующего алгоритма:

1) Если функция f(x) на концах отрезка [a, b] принимает значения разных знаков, то делим отрезок на 10 равных частей и находим ту часть, которая содержит корень (таким способом мы можем уменьшить длину отрезка, содержащего корень, в 10 раз).

2) Повторим действия предыдущего пункта для полученного отрезка.

Этот процесс можно продолжать до тех пор, пока длина отрезка не станет меньше заданной погрешности.

Пример 2.2. Отделить корни уравнения sin x + x – 1 = 0.

Решение. Найдем производную функции f(x) = sin x + x – 1 и её корни:

Функция f(x) = sin x + x – 1 монотонна на отрезках [– π + 2πk, π + 2πk]. Очевидно, что лишь отрезок [– π, π] содержит корень и он единственный.

Пример 2. 3.Вычислить графически с точностью до 0,0001 корень уравнения sin5x + x 2 – 1 = 0, принадлежащий интервалу (0,4; 0,5).

Решение. Построим график функции y = sin5x + x 2 – 1 на отрезке
[0,4; 0,5] с шагом h = 0,01 (делим отрезок на 10 частей) в программе Excel:

1) В диапазоне A2:A12 введем значения переменной x. Для этого в ячейке A2 запишем 0,40, в ячейке A3 — значение 0,41. После этого выделим диапазон A2:A3 и с помощью маркера заполнения присвоим значения остальным ячейкам до ячейки A12.

2) В ячейку B2 введем формулу =SIN(5*A2)+A2^2–1 и скопируем B2 с помощью маркера заполнения в остальные ячейки до ячейки B12.

3) Выделим диапазон A2:B12 и с помощью мастера диаграмм (тип диаграммы “Точечная”!) построим график функции.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Практическая часть. Задание 1. Отделите корни заданного уравнения, пользуясь графическим методом (схематически, на бумаге)

Задание 1. Отделите корни заданного уравнения, пользуясь графическим методом (схематически, на бумаге), а затем с помощью инструментального пакета Excel (см. рис 2.3). Это же задание выполните с помощью функции “Подбор параметра” (см. рис. 2.8).

Задание 2.По методу половинного деления (Ньютона, хорд) вычислите один корень заданного уравнения с точностью 10 -3 (10 -6 для методов Ньютона и хорд)

1. с помощью “ручной” расчетной таблицы и калькулятора;
2. с помощью программы, составленной в Excel (указание: необходимо использовать логические функции Excel “И, ИЛИ, ЕСЛИ”, а также включить функцию “Итерации” в меню Сервис→Параметры→Вычисления, см. Приложение 1).

Сопоставьте и прокомментируйте полученные результаты.

Варианты заданий приведены в табл. 2.1.

Пояснения к выполнению лабораторной работы № 2

При выполнении задания 1 отделение корней заданного уравнения выполняется с помощью схематического графика на бумаге. Во многих случаях задачу графического отделения корня можно упростить, заменив исходное уравнение вида F(x)=0 равносильным ему уравнением .Для решения этой же задачи с помощью компьютера используется инструментальный пакет Excel. Строится таблица значений функции и аргумента с определенным шагом. Задание шага может варьироваться в зависимости от величины выбранного участка и характера поведения функции F(x). Результатом выполнения задания должен быть перечень отрезков, содержащих по одному корню уравнения (см. примеры 2.1, 2.2, а также рис. 4, 5, 6). Затем отделение корней выполняется с помощью функции “Подбор параметра” в меню “Сервис” (см. рис. 11).

При выполнении задания 2 сначала уточняется один корень заданного уравнения по методу половинного деления (Ньютона, хорд) с заданной точностью с помощью “ручной” расчетной таблицы и калькулятора. Если корней несколько, то выбирается любой из участков, содержащий корень, подлежащий уточнению. Форма расчетной таблицы, которую можно использовать для организации “ручных” вычислений, показана ниже (пример приведен для метода половинного деления):

Далее для расчета используется инструментальный пакет Excel, составляется алгоритм для расчета корня уравнения с использованием функций этого пакета. После выполнения заданий требуется сравнить полученные результаты и сопоставить в них верные цифры.

Видео:Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Отделение корней

Приближенное значение корня может быть определено различными способами.

Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Графический метод отделения корней

Пусть требуется отделить корни уравнения (2.1). Строим график функции Дх) = 0. Абсциссы точек пересечения графика функции с осью ОХ будут приближенными значениями корней уравнения (2.1).

Часто уравнение (2.1) преобразовывают к более простому виду. Допустим:

Строим графики функций: yi = cpi(x); и yi=q>i(x). Корнями уравнения (2.3) будут являться абсциссы пересечения этих графиков.

Пример 2.1. Отделить корни уравнения /(х) = х ? lgx — 1=0. Преобразуем уравнениеДх) к виду:

Построим графики функций у, = lg х ну₂ = 1/х (рис. 2.1).

Рис. 2.1. Графический метод отделения корней

Точка пересечения графиков дает приближенное значение единственного корня ?, а 2,5.

Видео:Графический метод решения уравнений 8 классСкачать

Аналитический метод отделения корней

Теорема. Если непрерывная функция /(х) принимает значения разных знаков на концах отрезка [а, Ь

При заданных значениях х от — оо до + определяются знаки функции Дх). Результаты поиска приведены в таблице.

📸 Видео

7 класс, 35 урок, Графическое решение уравненийСкачать

Отбор корней по окружностиСкачать

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Решение системы уравнений графическим методомСкачать

Как построить график линейной функции.Скачать

Графический метод решения задачи линейного программирования (ЗЛП)Скачать

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

8 класс, 21 урок, Графическое решение уравненийСкачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Графический метод решения уравнений | Математика легко | ЦТ, ЦЭ, ЕГЭ | Решение задач по математикеСкачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Как построить график функции без таблицыСкачать

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Как решают уравнения в России и США!?Скачать

Графический способ решения уравнений и неравенств | Алгебра 10 классСкачать