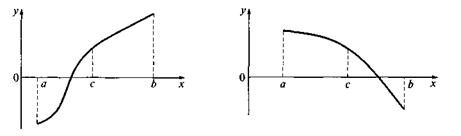
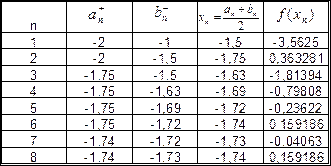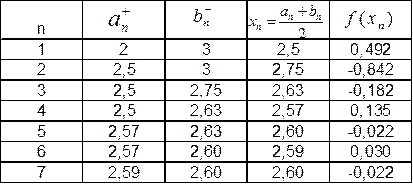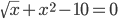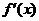Один из методов уточнения корней уравнения (1) – метод половинного деления. Исходные данные: уравнение f(x)=0; отрезок [a,b], на котором существует единственный корень уравнения (корень отделен), т.е. f(x) удовлетворяет условиям: f(x) непрерывна на [a,b], монотонна нем и f(a)f(b) 0 (знаки функции f(x) в точках a и c одинаковы), то левый конец отрезка заменяется на середину (а=с) иначе правый конец заменяется на середину (b=c).
4. Если длина отрезка не превосходит заданной точности (b-a 4 -x 3 -2x 2 +3x-3=0.
Полагая f(x)= x 4 -x 3 -2x 2 +3x-3, имеем f’(x)=4x 3 -3x 2 -4x+3.
Найдем нули производной: 4x 3 -3x 2 -4x+3=0; 4x(x 2 -1)-3(x 2 -1)=0;(x 2 -1)(4x-3)=0;
Составим таблицу знаков функции f(x):
| x | -∞ | -1 | 3/4 | +∞ | |
| f(x) | + | — | — | — | + |
Из таблицы видно, что уравнение имеет два действительных корня x1 
(-∞;-1) и x2 (1;+ ∞). Уменьшим промежутки, на которых находятся корни, до единичной длины:
| x | -2 | -1 | ||
| f(x) | + | — | — | + |
Следовательно, x1 (-2;-1) и x2 (1;2).
Уточним один из корней, например, x1, методом половинного деления до сотых долей. Все вычисления удобно производить, используя следующую таблицу:
Второй корень, уточняемый аналогичным образом, равен 1,73.
2. Отделить корни графически и уточнить их методом половинного деления.
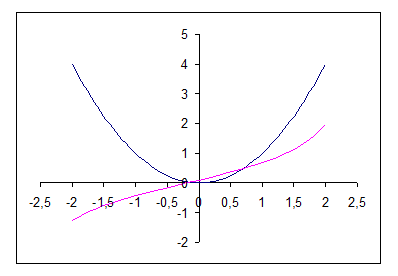
Перепишем уравнение в виде 
. Обозначим 
, 
и построим графики этих функций:
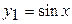
Из рисунка видно, что уравнение имеет три корня: точный x=0 и еще два, расположенных симметрично на отрезках [-3;-2] и [2;3].
Уточним корень на отрезке [2;3]:
Задания
1)Отделить корни аналитически и уточнить их методом половинного деления до 0,01, используя электронные таблицы.
1. 3x 4 +4x 3 -12x 2 -5=0
2. 2x 3 -9x 2 -60x+1=0
5. 3x 4 +3x 3 +6x 2 -10=0
7. x 4 +4x 3 -3x 2 -17=0
8. x 4 -x 3 -2x 2 +3x-3=0
9. 3x 4 +4x 3 -12x 2 +1=0
10. 3x 4 -8x 3 -18x 2 +2=0
11. 2x 4 -3x 3 +8x 2 -1=0
12. 2x 4 +8x 3 +3x 2 -1=0
13. x 4 -4x 3 -8x 2 +1=0
14. 3x 4 +4x 3 -12x 2 -5=0
15. 2x 3 -8x 2 -30x+1=0
17. 2x 4 -2x 2 -7=0
18. 3x 4 +8x 3 +6x 2 -10=0
19. x 4 -18x 2 +6=0
20. x 4 +4x 3 -3x-7=0
21. x 4 -2x 3 -x 2 +3x-3=0
22. 3x 4 +4x 3 -3x 2 -17=0
23. 2x 4 -5x 3 -12x 2 +2=0
24. 3x 4 +9x 3 -14x 2 +1=0
25. x 4 +2x 3 -x-1=0
26. x 4 +8x 3 -6x 2 -72x=0
28. x 4 -3x 2 +75x-10000=0
2) Отделить корни графически и уточнить их методом половинного деления до 0.01, используя электронные таблицы.
Лабораторная работа №3
Решение нелинейных уравнений методом хорд
Краткая теория
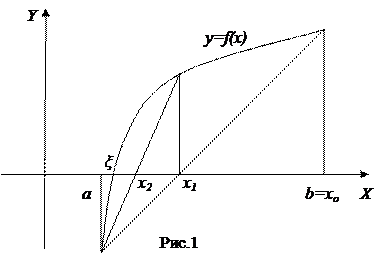
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Уточним этот корень методом хорд. Геометрически метод хорд означает замену на отрезке [a,b] графика функции y=f(x) хордой, проведенной через точки (a,f(a)) и (b,f(b)):
Здесь ξ — точный корень уравнения (1), x 
— начальное приближение к корню, x 
-точка пересечения хорды с осью Ох – первое приближение к корню. Далее метод хорд применяется на отрезке [a, x ] и получается второе приближение к корню — x 
. В случае, изображенном на рис.1, конец отрезка а остается неподвижным. Из уравнения хорды и условия, что точка (x ,0) принадлежит хорде, получается формула для вычисления n-го приближения к корню для случая, когда а – неподвижный конец: x =b,
x 
=a- 
(2)
Для случая неподвижного конца b используется формула: x =a,
x =x 
— 
(3)
Правило определения неподвижного конца хорды:
Если знаки первой и второй производных функции f(x) на отрезке [a, b] совпадают, то неподвижным являются конец b, иначе — конец a.
Метод хорд обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длину n-го отрезка: 
1. Определить, какой конец отрезка будет неподвижным и принять за x другой конец отрезка.
2. Вычислить новое приближение к корню x по формуле (2) или (3).
3. Если длина отрезка [x , x ] не превосходит заданной точности, то процесс заканчивается и в качестве точного корня можно взять x или x , иначе идти к п.2
Решение одного варианта
1.Отделить корни графически и уточнить их методом хорд с точностью до 0.001: tg(0.5x+0.1)=x 
.
Отделим корень графически. Построим графики функций
y =tg(0.5x+0.1) и y =x :
Таким образом, уравнение имеет два корня
x [0.5; 1] и x [-0.5; 0]
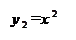
Чтобы уточнить этот корень методом хорд, определим знаки первой и второй производной функции f(x)= tg(0.5x+0.1)-x на промежутке [0.5;1]. Имеем
f ‘(x)=0.5/cos (0.5x+0.1)-2x;
3. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. x lgx — 1.2 = 0
14. 1.8x 2 – sin10x = 0
15. ctgx – x / 4 = 0
16. tg(0.3x + 0.4) = x 2
17. x – 20sinx = 0
18. ctgx – x / 3 = 0
19. tg(0.47x + 0.2) = x 2
20. x 2 + 4sinx = 0
21. ctgx – x / 2 = 0
22. 2x – lgx – 7 = 0
24. 3x – cosx – 1 = 0
26. 10cosx-0,1x 2 =0
2)Отделить корни аналитически и уточнить их методом хорд до 0.001:
Видео:Метод половинного деления решение нелинейного уравненияСкачать
Метод половинного деления (метод дихотомии или метод бисекции)
Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξi являющихся приближением корня на i -ом шаге.
ξi=½(bi+ai), i=0,1.
где a0=a; b0=b; ai;bi — границы подынтервалов, в которых f(ai)f(bi) 0 мы ни задали, всегда можно найти такое n , что 
ч.т.д.
Графически метод дихотомии выглядит следующим образом
|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.
Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].
- Решение
- Видео решение
Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3
Найдем корни уравнения: 
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 2.6 | 3 | 2.8 | -1.6275 | -0.4867 |
| 2 | 2.8 | 3 | 2.9 | -0.4867 | 0.1129 |
| 3 | 2.8 | 2.9 | 2.85 | 0.1129 | -0.1893 |
| 4 | 2.8 | 2.85 | 2.825 | -0.1893 | -0.3386 |
| 5 | 2.825 | 2.85 | 2.8375 | -0.3386 | -0.2641 |
| 6 | 2.8375 | 2.85 | 2.8438 | -0.2641 | -0.2267 |
Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн
Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε1 = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε2 = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε2 число итераций.
Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать
Уточнение корня уравнения методом половинного деления
Пояснения к работе
2.1 Краткие теоретические сведения:
Отделение корней
Пусть имеется уравнение вида
где f (х) — алгебраическая или трансцендентная функция. Напомним, что функция называется алгебраической, если для получения значения функции по данному значению х нужно выполнить арифметические операции и возведение в степень с рациональным показателем. К трансцендентным функциям относятся все неалгебраические функции – показательная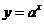 
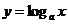
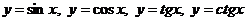
, логарифмическая 
, тригонометрические 
и обратные тригонометрические 
.
Решить уравнение (1) — значит установить, имеет ли оно корни, сколько корней, и найти значения корней с требуемой точностью. Решение указанной задачи в общем случае начинают с этапа отделения корней, который заключается в установлении количества корней, а также наиболее тесных промежутков, каждый из которых содержит только один корень.
Грубое отделение корней во многих случаях можно произвести графическим методом. При этом задачу часто удается сильно упростить, заменив уравнение (1) равносильным ему уравнением
В этом случае строятся графики функций f1(х) и f2(x), а потом на оси ОХ отмечаются по возможности наименьшие отрезки, локализующие абсциссы точек пересечения этих графиков с осью ОХ.
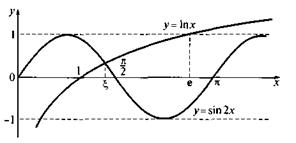
Пример 1.Для графического отделения корней уравнения sin2х- 1n х = 0 преобразуем его к равносильному уравнению sin2х = lnх и отдельно построим графики функций sin2х и lnx (рис. 1).
Из графика вполне очевидно, что уравнение имеет единственный корень ξ и этот корень находится на отрезке [1; 1,5].
Рис. 1 Графическое отделение корня уравнения sin2х-lnx = 0
При решении задачи об отделении корней бывают полезными следующие очевидные
1) если непрерывная на отрезке [а; b] функция f (х) принимает на его концах значения разных знаков (т.е. f (а) f (b) 0, так что отрезком, на котором находится корень, можно считать [1,3; 1,5].
В простейших случаях графическое отделение корней можно осуществить вручную, однако в более сложных случаях для исследования вопроса о наличии (и количестве) корней уравнения на заданном отрезке целесообразнее воспользоваться инструментальным пакетом или составить программу для ЭВМ на языке программирования. Рассмотрим коротко суть идеи для применения указанных подходов.
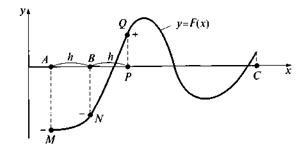
Пусть имеется уравнение f (х) = 0, причем известно, что все интересующие вычислителя корни находятся на отрезке [А; В], в котором функция f (х) определена, непрерывна и f (А) f (В)
Рис. 2 Иллюстрация к процессу отделения корней
Кроме графического способа отделения корней существует аналитический методотделения корней. Опишем порядок действий при нем:
1. Найти 
2. Составить таблицу знаков функции f(x), полагая х равным: а) критическим значениям (корням) производной или ближайшим к ним; б) граничным значениям (исходя и области допустимых значений неизвестного)
3. Определить интервалы, на концах которых функция принимает значения противоположных знаков. Внутри этих интервалов содержится по одному и только одному корню.
Пример 2.Отделить корни уравнения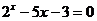 
аналитическим методом.
Решение: обозначим 
. Область определения функции f(x) – вся числовая ось. Найдем первую производную: 
. Найдем критические точки:
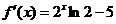
Составим таблицу знаков функции f(x), полагая х равным а) критическим значениям производной или ближайшим к ним; б) граничным значениям (из области допустимых значений неизвестного):
| х |  |  | ||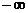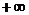
| знак f(x) | + | — | — | + |
Уравнение имеет два корня, т.к. происходит две смены знака функции. Составим новую таблицу, с более мелким интервалом изоляции корня
| х | -1 | ||||||
| знак f(x) | + | — | — | — | — | — | + |
Корни уравнения находятся в промежутках (-1; 0) и (4; 5)
Уточнение корня уравнения методом половинного деления
Второй этап приближенного решения алгебраических и трансцендентных уравнений – уточнение корней.
Пусть уравнение f (х) = 0 имеет на отрезке [а; b] единственный корень, причем функция f(х) на этом отрезке непрерывна. Разделим отрезок [а; b] пополам точкой с = (а + b )/2. Если
f (с)≠0 (что наиболее вероятно), то возможны два случая: либо f (х) меняет знак на отрезке [a; с] (рис. 3, а), либо на отрезке [с; b](рис. 3, б).
К решению уравнения f (х) = 0 методом половинного деления
Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая
процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего
Рассмотренный метод, его называют методом половинного деления(другое название — метод дихотомии), можно использовать как метод решения уравнения с заданной точностью.
Действительно, если на каком-то этапе процесса получен отрезок [а; b], содержащий корень, то, приняв приближенно х=(а + b)/2, получим ошибку, не превышающую значения
(заметим, что речь в данном случае идет о погрешности метода). Метод половинного деления требует утомительных ручных вычислений, однако он легко реализуется с помощью программы на ЭВМ.
Пример 3. Методом половинного деления уточнить до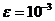 
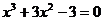
меньший корень уравнения
.
Решение: отделим корни этого уравнения аналитически. Функция f(х) определена на всей числовой оси. Приравняем производную нулю и найдем критические точки:
.
Составим таблицу знаков функции:
| х | 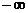| -2 | -1 | | ||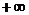
| знак f(x) | — | + | — | — | + | + |
Из таблицы видим, что левый корень принадлежит интервалу ( 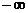; -2). Возьмем для пробы 
. Тогда получим таблицу: 
| х | -3 | -2 | -1 | ||
| знак f(x) | — | + | — | — | + |
Следовательно, корни уравнения принадлежат промежуткам (-3; -2); (-2; -1); (0; 1). Уточним меньший корень, лежащий в интервале (-3; -2), метом половинного деления. Для удобства вычислений составим таблицу (знаки «-» и «+» в верхних индексах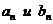 
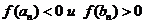
означают, что 
)
| п |  |  |  |  |  |  |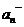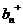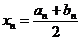
| -3 | -2 | -2,500 | -15,625 | 18,750 | 0,125 | |
| -3 | -2.500 | -2,750 | -20,800 | 22,689 | -1,111 | |
| -2,750 | -2.500 | -2.625 | -17, 90 | 20,670 | -0,320 | |
| -2,625 | -2,500 | -2,563 | -16,840 | 19,701 | -0,130 | |
| -2,563 | -2,500 | -2,532 | -16,230 | 19,233 | 0,003 | |
| -2,563 | -2,532 | -2,548 | -16,540 | 19,479 | -0,071 | |
| -2,548 | -2,532 | -2,540 | -16,390 | 19,356 | -0,034 |
| -2,540 | -2,532 | -2,536 | -16,310 | 19,293 | -0,014 |
| -2,536 | -2,532 | -2,534 | -16,270 | 19,263 | -0,007 |
| -2.534 | -2,532 | -2,533 | -16, 250 | 19,248 | -0,002 |
| -2,533 | -2,532 |
Итак, корень уравнения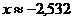 
.
💡 Видео
Метод половинного деления. ДихотомияСкачать
Метод Ньютона (метод касательных) Пример РешенияСкачать
8 Метод половинного деления Calc Excel Численные методы решения нелинейного уравненияСкачать
14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать
Как найти корни уравнения в Excel с помощью Подбора параметраСкачать
Метод половинного деления - ВизуализацияСкачать
6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать
Численное решение уравнений, урок 2/5. Метод деления отрезка пополамСкачать
Метод дихотомииСкачать
Урок 10. C++ Метод половинного деленияСкачать
Метод простых итераций пример решения нелинейных уравненийСкачать
3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать
Найти корень уравнения на заданном интервале (MathCad)Скачать
Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Метод хордСкачать
Отбор корней по окружностиСкачать
