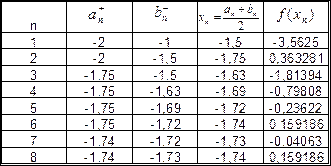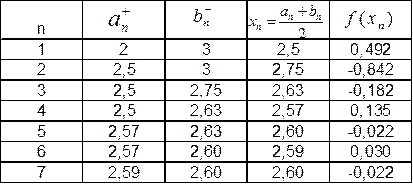В этом разделе приведены примеры решенных задач по теме нахождения корней нелинейных уравнений численными методами. На первом этапе обычно происходит локализация (отделение) корней (графически или аналитически), на втором — уточнение (поиск) корней разными методами: Ньютона, Стеффенсена, секущих, хорд, касательных, простой итерации.
Видео:Метод хордСкачать
Примеры приближенных решений нелинейных уравнений онлайн
Задача 1. Методом бисекции найти решение нелинейного уравнения на отрезке $[a;b]$ с точностью $varepsilon = 10^$. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью $varepsilon=10^$. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
Задача 2. Отделить корни нелинейного уравнения аналитически $2 arcctg x -x+3=0$.
Задача 3. Отделить корни нелинейного уравнения аналитически и уточнить один из них методом проб с точностью до 0,01. $$3x^4-8x^3-18x^2+2=0.$$
Задача 4. Отделить корни нелинейного уравнения графически (например, в среде EXCEL) уточнить один из них методом проб с точностью до 0,01. $$x^2-20 sin x =0.$$
Задача 5. Отделите корни уравнения графически и уточните один из них методом хорд с точностью до 0,001. Уточните один из корней этого уравнения методом касательных с точностью до 0,001. $$ sqrt — cos 0.387 x =0.$$
Задача 6.Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. $$sqrt=frac.$$
Задача 7. На отрезке $[0;2]$ методом Ньютона найти корень уравнения $-x^3-2x^2-4x+10=0$ с точностью 0,01.
Задача 8. Методом хорд найти отрицательный корень уравнения $x^3-2x^2-4x+7=0$ с точностью 0,0001. Требуется предварительное построение графика функции и отделение корней.
Задача 9. Решить нелинейные уравнения с точностью до 0.001. $$1), x^3-12x-5=0, (x gt 0), , 2), tan x -1/x=0. $$
Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать
Метод хорд
Метод хорд — итерационный численный метод приближённого нахождения корня уравнения.
Немного теории о методе хорд под калькулятором.
Метод хорд
Метод хорд
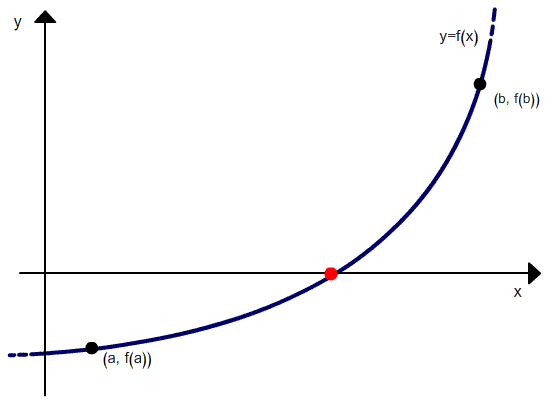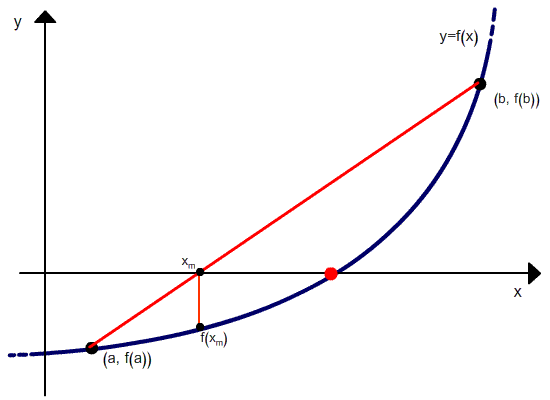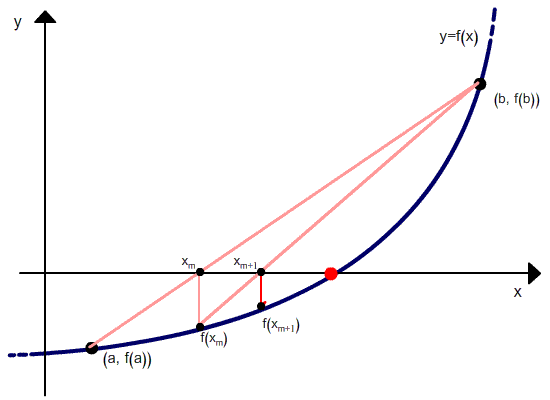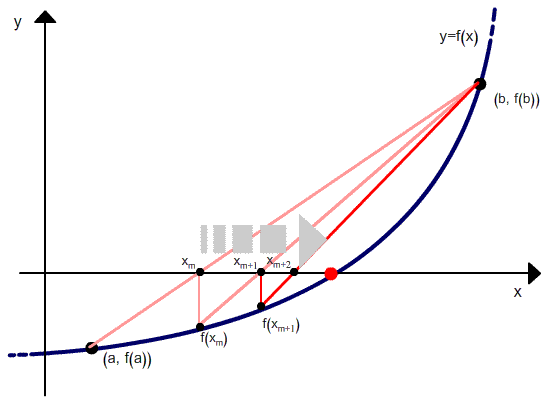
Метод хорд можно рассматривать как комбинацию метода секущих (Метод секущих) и метода дихотомии — отличие от метода секущих состоит в том, что если в методе секущих в качестве точек следующей итерации выбираются последние рассчитанные точки, то в методе хорд выбираются те точки, в которых функция имеет разный знак, и соответственно, выбранный интервал содержит корень.
Вывод итерационной формулы аналогичен выводу формулы для метода секущих:
Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет
Для точки пересечения с осью абсцисс (у=0) получим уравнение
Но в отличие от метода секущих, после расчета следующего приближения в качестве второй точки выбирается не последняя, а та, в которой функция имеет разный знак со значением функции в вычисленной точке. Проиллюстрировано это ниже.
Метод хорд является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале), при этом величина интервала в процессе итераций не стремится к 0.
В качестве критерия останова берут один из следующих:
— значение функции на данной итерации стало меньше заданого ε.
— изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать
Метод половинного деления. Один из методов уточнения корней уравнения (1) – метод половинного деления
Один из методов уточнения корней уравнения (1) – метод половинного деления. Исходные данные: уравнение f(x)=0; отрезок [a,b], на котором существует единственный корень уравнения (корень отделен), т.е. f(x) удовлетворяет условиям: f(x) непрерывна на [a,b], монотонна нем и f(a)f(b) 0 (знаки функции f(x) в точках a и c одинаковы), то левый конец отрезка заменяется на середину (а=с) иначе правый конец заменяется на середину (b=c).
4. Если длина отрезка не превосходит заданной точности (b-a 4 -x 3 -2x 2 +3x-3=0.
Полагая f(x)= x 4 -x 3 -2x 2 +3x-3, имеем f’(x)=4x 3 -3x 2 -4x+3.
Найдем нули производной: 4x 3 -3x 2 -4x+3=0; 4x(x 2 -1)-3(x 2 -1)=0;(x 2 -1)(4x-3)=0;
Составим таблицу знаков функции f(x):
| x | -∞ | -1 | 3/4 | +∞ | |
| f(x) | + | — | — | — | + |
Из таблицы видно, что уравнение имеет два действительных корня x1 
(-∞;-1) и x2 (1;+ ∞). Уменьшим промежутки, на которых находятся корни, до единичной длины:
| x | -2 | -1 | ||
| f(x) | + | — | — | + |
Следовательно, x1 (-2;-1) и x2 (1;2).
Уточним один из корней, например, x1, методом половинного деления до сотых долей. Все вычисления удобно производить, используя следующую таблицу:
Второй корень, уточняемый аналогичным образом, равен 1,73.
2. Отделить корни графически и уточнить их методом половинного деления.
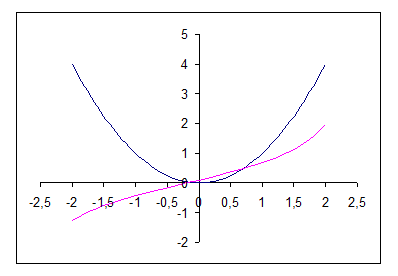
Перепишем уравнение в виде 
. Обозначим 
, 
и построим графики этих функций:
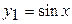
Из рисунка видно, что уравнение имеет три корня: точный x=0 и еще два, расположенных симметрично на отрезках [-3;-2] и [2;3].
Уточним корень на отрезке [2;3]:
Задания
1)Отделить корни аналитически и уточнить их методом половинного деления до 0,01, используя электронные таблицы.
1. 3x 4 +4x 3 -12x 2 -5=0
2. 2x 3 -9x 2 -60x+1=0
5. 3x 4 +3x 3 +6x 2 -10=0
7. x 4 +4x 3 -3x 2 -17=0
8. x 4 -x 3 -2x 2 +3x-3=0
9. 3x 4 +4x 3 -12x 2 +1=0
10. 3x 4 -8x 3 -18x 2 +2=0
11. 2x 4 -3x 3 +8x 2 -1=0
12. 2x 4 +8x 3 +3x 2 -1=0
13. x 4 -4x 3 -8x 2 +1=0
14. 3x 4 +4x 3 -12x 2 -5=0
15. 2x 3 -8x 2 -30x+1=0
17. 2x 4 -2x 2 -7=0
18. 3x 4 +8x 3 +6x 2 -10=0
19. x 4 -18x 2 +6=0
20. x 4 +4x 3 -3x-7=0
21. x 4 -2x 3 -x 2 +3x-3=0
22. 3x 4 +4x 3 -3x 2 -17=0
23. 2x 4 -5x 3 -12x 2 +2=0
24. 3x 4 +9x 3 -14x 2 +1=0
25. x 4 +2x 3 -x-1=0
26. x 4 +8x 3 -6x 2 -72x=0
28. x 4 -3x 2 +75x-10000=0
2) Отделить корни графически и уточнить их методом половинного деления до 0.01, используя электронные таблицы.
Лабораторная работа №3
Решение нелинейных уравнений методом хорд
Краткая теория
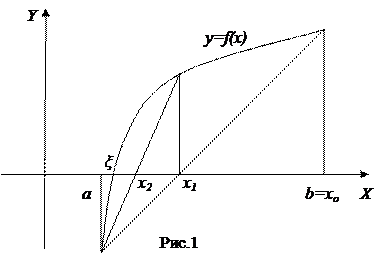
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Уточним этот корень методом хорд. Геометрически метод хорд означает замену на отрезке [a,b] графика функции y=f(x) хордой, проведенной через точки (a,f(a)) и (b,f(b)):
Здесь ξ — точный корень уравнения (1), x 
— начальное приближение к корню, x 
-точка пересечения хорды с осью Ох – первое приближение к корню. Далее метод хорд применяется на отрезке [a, x ] и получается второе приближение к корню — x 
. В случае, изображенном на рис.1, конец отрезка а остается неподвижным. Из уравнения хорды и условия, что точка (x ,0) принадлежит хорде, получается формула для вычисления n-го приближения к корню для случая, когда а – неподвижный конец: x =b,
x 
=a- 
(2)
Для случая неподвижного конца b используется формула: x =a,
x =x 
— 
(3)
Правило определения неподвижного конца хорды:
Если знаки первой и второй производных функции f(x) на отрезке [a, b] совпадают, то неподвижным являются конец b, иначе — конец a.
Метод хорд обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длину n-го отрезка: 
1. Определить, какой конец отрезка будет неподвижным и принять за x другой конец отрезка.
2. Вычислить новое приближение к корню x по формуле (2) или (3).
3. Если длина отрезка [x , x ] не превосходит заданной точности, то процесс заканчивается и в качестве точного корня можно взять x или x , иначе идти к п.2
Решение одного варианта
1.Отделить корни графически и уточнить их методом хорд с точностью до 0.001: tg(0.5x+0.1)=x 
.
Отделим корень графически. Построим графики функций
y =tg(0.5x+0.1) и y =x :
Таким образом, уравнение имеет два корня
x [0.5; 1] и x [-0.5; 0]
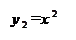
Чтобы уточнить этот корень методом хорд, определим знаки первой и второй производной функции f(x)= tg(0.5x+0.1)-x на промежутке [0.5;1]. Имеем
f ‘(x)=0.5/cos (0.5x+0.1)-2x;
3. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. x lgx — 1.2 = 0
14. 1.8x 2 – sin10x = 0
15. ctgx – x / 4 = 0
16. tg(0.3x + 0.4) = x 2
17. x – 20sinx = 0
18. ctgx – x / 3 = 0
19. tg(0.47x + 0.2) = x 2
20. x 2 + 4sinx = 0
21. ctgx – x / 2 = 0
22. 2x – lgx – 7 = 0
24. 3x – cosx – 1 = 0
26. 10cosx-0,1x 2 =0
2)Отделить корни аналитически и уточнить их методом хорд до 0.001:
📸 Видео
1,2 Решение нелинейных уравнений методом хордСкачать
Алгоритмы. Нахождение корней уравнения методом хордСкачать
Метод половинного деления. ДихотомияСкачать
метод хордСкачать
Численное решение уравнений, урок 3/5. Метод хордСкачать
Метод итерацийСкачать
Метод половинного деления решение нелинейного уравненияСкачать
14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать
Метод простых итераций пример решения нелинейных уравненийСкачать
15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать
7 класс, 35 урок, Графическое решение уравненийСкачать
11 Метод Ньютона (Метод касательных) Mathcad Численные методы решения нелинейного уравненияСкачать
1 3 Решение нелинейных уравнений методом простых итерацийСкачать
Метод касательных (метод Ньютона)Скачать
8 класс, 21 урок, Графическое решение уравненийСкачать
Численное решение уравнений, урок 2/5. Метод деления отрезка пополамСкачать
Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать
