В этом разделе приведены примеры решенных задач по теме нахождения корней нелинейных уравнений численными методами. На первом этапе обычно происходит локализация (отделение) корней (графически или аналитически), на втором — уточнение (поиск) корней разными методами: Ньютона, Стеффенсена, секущих, хорд, касательных, простой итерации.
- Примеры приближенных решений нелинейных уравнений онлайн
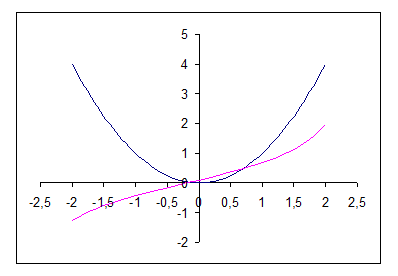
- математика. Контрольная работа № 1. Задание 1 Определить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. Решение
- Метод половинного деления. Один из методов уточнения корней уравнения (1) – метод половинного деления
- 🎬 Видео
Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Примеры приближенных решений нелинейных уравнений онлайн
Задача 1. Методом бисекции найти решение нелинейного уравнения на отрезке $[a;b]$ с точностью $varepsilon = 10^$. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью $varepsilon=10^$. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
Задача 2. Отделить корни нелинейного уравнения аналитически $2 arcctg x -x+3=0$.
Задача 3. Отделить корни нелинейного уравнения аналитически и уточнить один из них методом проб с точностью до 0,01. $$3x^4-8x^3-18x^2+2=0.$$
Задача 4. Отделить корни нелинейного уравнения графически (например, в среде EXCEL) уточнить один из них методом проб с точностью до 0,01. $$x^2-20 sin x =0.$$
Задача 5. Отделите корни уравнения графически и уточните один из них методом хорд с точностью до 0,001. Уточните один из корней этого уравнения методом касательных с точностью до 0,001. $$ sqrt — cos 0.387 x =0.$$
Задача 6.Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. $$sqrt=frac.$$
Задача 7. На отрезке $[0;2]$ методом Ньютона найти корень уравнения $-x^3-2x^2-4x+10=0$ с точностью 0,01.
Задача 8. Методом хорд найти отрицательный корень уравнения $x^3-2x^2-4x+7=0$ с точностью 0,0001. Требуется предварительное построение графика функции и отделение корней.
Задача 9. Решить нелинейные уравнения с точностью до 0.001. $$1), x^3-12x-5=0, (x gt 0), , 2), tan x -1/x=0. $$
Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

математика. Контрольная работа № 1. Задание 1 Определить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. Решение
| Название | Задание 1 Определить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. Решение |
| Анкор | математика |
| Дата | 19.03.2022 |
| Размер | 89.95 Kb. |
| Формат файла |  |
| Имя файла | Контрольная работа № 1.docx |
| Тип | Решение #404383 |
| Подборка по базе: практическое задание №4 Изъюров Л.С..docx, Практическое задание 1.doc, Практическое задание_2математика_Зейналова_Лейла.doc, Аналитическое задание педагогика ипз.docx, Практическое задание 2.rtf, Домашнее задание по колледжу.docx, Ответ на задание 1.1.docx, Практическое задание к теме 2.docx, Практическое задание №1.docx, Практическая работа №3. Задание №1.docx Определить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. Сначала нужно отделить решения. Удобно записать уравнение в виде Из графика следует, что корень один: x * ∈ [0;1]. Представим уравнение в форме: Найдем максимальное значение производной от функции Значение λ = 1/(8) ≈ 0.125 Таким образом, решаем следующее уравнение: Поскольку F(0)*F(1)
Ответ: x = 0.46359395923842; F(x) = -0.00693 Отделить корни уравнения графически и уточнить один из них методом касательных с точностью до 0,001 Сначала нужно отделить решения. Удобно записать уравнение в виде Из графика следует, что корень множество, возьмем: x * ∈ [0;1]. Сначала нужно выбрать начальное приближение. Вычислим несколько приближений: Решение получено за 4 итерации, так как поправка стала меньше заданной точности: Методом итераций решить систему линейныx уравнений с точностью до 0,001. Приведем к виду: На главной диагонали матрицы присутствует нулевой элемент. Его необходимо исключить. Поскольку 2.2609>1, то скорость итерационного процесса будет низкой. Необходимо сделать так, чтобы a → 0. Руководствуясь этим соображением, целесообразно сделать диагональное преобладание возможно более значительным (например, умножить какую-нибудь строку на коэффициент и прибавить к другой). N=1 N=2 N=3 Остальные расчеты сведем в таблицу.
Для оценки погрешности вычисляем коэффициент α: Методом Гаусса-Зейделя решить с точностью 0,001 систему линейных уравнений, приведя ее к виду, удобному для итераций. Приведем к виду: Покажем вычисления на примере нескольких итераций. N=1 N=2 N=3 Остальные расчеты сведем в таблицу.
Для оценки погрешности вычисляем коэффициент α: Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать  Метод половинного деления. Один из методов уточнения корней уравнения (1) – метод половинного деленияОдин из методов уточнения корней уравнения (1) – метод половинного деления. Исходные данные: уравнение f(x)=0; отрезок [a,b], на котором существует единственный корень уравнения (корень отделен), т.е. f(x) удовлетворяет условиям: f(x) непрерывна на [a,b], монотонна нем и f(a)f(b) 0 (знаки функции f(x) в точках a и c одинаковы), то левый конец отрезка заменяется на середину (а=с) иначе правый конец заменяется на середину (b=c). 4. Если длина отрезка не превосходит заданной точности (b-a 4 -x 3 -2x 2 +3x-3=0. Полагая f(x)= x 4 -x 3 -2x 2 +3x-3, имеем f’(x)=4x 3 -3x 2 -4x+3. Найдем нули производной: 4x 3 -3x 2 -4x+3=0; 4x(x 2 -1)-3(x 2 -1)=0;(x 2 -1)(4x-3)=0; Составим таблицу знаков функции f(x):
Из таблицы видно, что уравнение имеет два действительных корня x1
Следовательно, x1 Уточним один из корней, например, x1, методом половинного деления до сотых долей. Все вычисления удобно производить, используя следующую таблицу: Второй корень, уточняемый аналогичным образом, равен 1,73. 2. Отделить корни графически и уточнить их методом половинного деления. Перепишем уравнение в виде Из рисунка видно, что уравнение имеет три корня: точный x=0 и еще два, расположенных симметрично на отрезках [-3;-2] и [2;3]. Уточним корень на отрезке [2;3]: Задания 1)Отделить корни аналитически и уточнить их методом половинного деления до 0,01, используя электронные таблицы. 1. 3x 4 +4x 3 -12x 2 -5=0 2. 2x 3 -9x 2 -60x+1=0 5. 3x 4 +3x 3 +6x 2 -10=0 7. x 4 +4x 3 -3x 2 -17=0 8. x 4 -x 3 -2x 2 +3x-3=0 9. 3x 4 +4x 3 -12x 2 +1=0 10. 3x 4 -8x 3 -18x 2 +2=0 11. 2x 4 -3x 3 +8x 2 -1=0 12. 2x 4 +8x 3 +3x 2 -1=0 13. x 4 -4x 3 -8x 2 +1=0 14. 3x 4 +4x 3 -12x 2 -5=0 15. 2x 3 -8x 2 -30x+1=0 17. 2x 4 -2x 2 -7=0 18. 3x 4 +8x 3 +6x 2 -10=0 19. x 4 -18x 2 +6=0 20. x 4 +4x 3 -3x-7=0 21. x 4 -2x 3 -x 2 +3x-3=0 22. 3x 4 +4x 3 -3x 2 -17=0 23. 2x 4 -5x 3 -12x 2 +2=0 24. 3x 4 +9x 3 -14x 2 +1=0 25. x 4 +2x 3 -x-1=0 26. x 4 +8x 3 -6x 2 -72x=0 28. x 4 -3x 2 +75x-10000=0 2) Отделить корни графически и уточнить их методом половинного деления до 0.01, используя электронные таблицы. Лабораторная работа №3 Решение нелинейных уравнений методом хорд Краткая теория Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Уточним этот корень методом хорд. Геометрически метод хорд означает замену на отрезке [a,b] графика функции y=f(x) хордой, проведенной через точки (a,f(a)) и (b,f(b)): Здесь ξ — точный корень уравнения (1), x x Для случая неподвижного конца b используется формула: x x Правило определения неподвижного конца хорды: Если знаки первой и второй производных функции f(x) на отрезке [a, b] совпадают, то неподвижным являются конец b, иначе — конец a. Метод хорд обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длину n-го отрезка: 1. Определить, какой конец отрезка будет неподвижным и принять за x 2. Вычислить новое приближение к корню x 3. Если длина отрезка [x Решение одного варианта 1.Отделить корни графически и уточнить их методом хорд с точностью до 0.001: tg(0.5x+0.1)=x Отделим корень графически. Построим графики функций y Таким образом, уравнение имеет два корня Чтобы уточнить этот корень методом хорд, определим знаки первой и второй производной функции f(x)= tg(0.5x+0.1)-x 3. 6. 7. 8. 9. 10. 11. 12. 13. x lgx — 1.2 = 0 14. 1.8x 2 – sin10x = 0 15. ctgx – x / 4 = 0 16. tg(0.3x + 0.4) = x 2 17. x – 20sinx = 0 18. ctgx – x / 3 = 0 19. tg(0.47x + 0.2) = x 2 20. x 2 + 4sinx = 0 21. ctgx – x / 2 = 0 22. 2x – lgx – 7 = 0 24. 3x – cosx – 1 = 0 26. 10cosx-0,1x 2 =0 2)Отделить корни аналитически и уточнить их методом хорд до 0.001: 🎬 ВидеоУрок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать  Найти корень уравнения на заданном интервале (MathCad)Скачать  Метод половинного деления. ДихотомияСкачать  Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать  14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать  АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать  Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать  Метод половинного деления решение нелинейного уравненияСкачать  Решение биквадратных уравнений. 8 класс.Скачать  Как найти корни уравнения в Excel с помощью Подбора параметраСкачать  8 класс, 21 урок, Графическое решение уравненийСкачать  Как решать дробно-рациональные уравнения? | МатематикаСкачать  Графический метод решения уравнений 8 классСкачать  Метод касательных (метод Ньютона)Скачать  5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать  Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать  Метод хордСкачать  |

 и построить графики двух элементарных функций
и построить графики двух элементарных функций



 и построить графики двух элементарных функций
и построить графики двух элементарных функций














 (-∞;-1) и x2
(-∞;-1) и x2 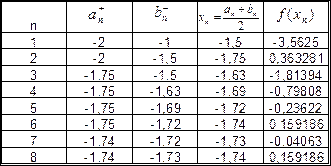

 . Обозначим
. Обозначим  ,
,  и построим графики этих функций:
и построим графики этих функций:


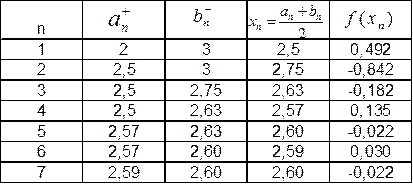

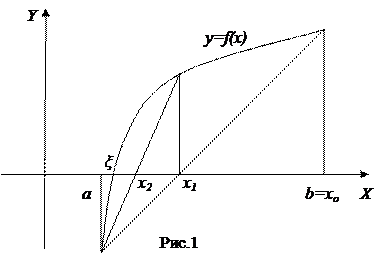
 — начальное приближение к корню, x
— начальное приближение к корню, x  -точка пересечения хорды с осью Ох – первое приближение к корню. Далее метод хорд применяется на отрезке [a, x
-точка пересечения хорды с осью Ох – первое приближение к корню. Далее метод хорд применяется на отрезке [a, x  . В случае, изображенном на рис.1, конец отрезка а остается неподвижным. Из уравнения хорды и условия, что точка (x
. В случае, изображенном на рис.1, конец отрезка а остается неподвижным. Из уравнения хорды и условия, что точка (x  =a-
=a-  (2)
(2) —
—  (3)
(3)
 .
.
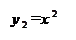 x
x  f ‘(x)=0.5/cos
f ‘(x)=0.5/cos 






