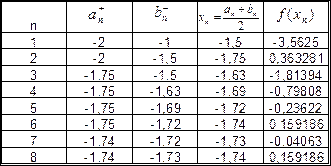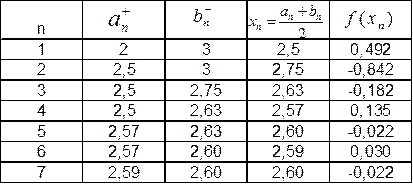Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать
Уточнение корня методом проб
Пусть дано уравнениеДх) = 0 и некоторый корень с, отделен на отрезке [а; Ь]. Обозначим b -а = d (это длина отрезка). Требуется найти приближенное значение корня о с точностью до 10″* (т.е. с погрешностью, не превышающей 10“*). Заметим, что а ], т.е. число
Абсолютная погрешность этого приближенного числа меньше половины длины отрезка [а; Ь], т.е.
Значит, за приближенное значение корня выгоднее принять не концы отрезка [а; b], а его середину с (рис. 2.9).
Рис. 2.9. Корень уравнения и его приближения
Пусть теперь отрезок [а; Ь] таков, что его длина больше предельной абсолютной погрешности искомого корня, т.е. больше, чем 10″*. Тогда путем последовательного деления отрезок, на котором отделен корень, уменьшают до тех пор, пока его длина не сделается меньше, чем заданная предельная абсолютная погрешность корня.
На практике отрезок, на котором отделен корень, делят либо пополам, либо на 10 равных частей. В первом случае говорят о методе проб с половинным делением, а во втором — о методе проб с десятичным делением.
Для программирования на ЭВМ удобен метод проб с половинным делением, а для ручного счета, в том числе и с помощью Microsoft Excel, — с десятичным.
Найдите корень уравнения х 3 — бх 2 + 20 = 0 на отрезке [2; 3] с точностью до 10- 7 методом проб.
На персональном компьютере (ПК) откроем новую книгу Microsoft Excel, назовем ее «Решение уравнений» и переименуем ее первый лист так: «Метод десятичного деления». В ячейку А1 поместим символ х, в ячейку В1 — f(x). В ячейки А2—А12 поместим последовательно значения аргумента от 2 до 3 с шагом ОД. В ячейку В2 вставим формулу
Эта формула соответствует левой части данного уравнения. Вычислим данное значение. Протянем ячейку В2 до ячейки В12. В этих ячейках получим значения функции Дх), соответствующей левой части уравнения. В ячейках А2—А12 найдем те два соседних значения аргумента, для которых значения функции, находящиеся в ячейках В2—В12, меняют знак. В данном случае это значения 2,3 и 2,4 (на рис. 2.10 эти ячейки выделены).
Далее снова в ячейку С1 поместим символ х, в ячейку Dl—f(x). В ячейки С2—С12 поместим последовательно значения аргумента от 2,3 до 2,4 с шагом 0,01. В ячейку D2 вставим формулу
Протянем ячейку D2 до ячейки D12. В этих ячейках получим значения функции Дх), соответствующей левой части уравнения. В ячейках С2—С12 найдем те два соседних значения аргумента, для которых значения функции, находящиеся в ячейках D2—D12, меняют знак (на рис. 2.10 эти ячейки выделены).
Повторяем описанный выше процесс до тех пор, пока не получим восемь значащих цифр чисел 2,33650880 и 2,33650881, между которыми лежит значение корня данного уравнения (рис. 2.10).
Рис. 2.10. Вычисление корня уравнения х3 — бх2 + 20 = 0 на отрезке [2; 3] методом десятичного деления
Округляя эти числа до 7 цифр после запятой, получаем приближенное значение корня уравнения х 3 — бх 2 + 20 = 0 из отрезка [2; 3] с точностью до 1СГ 7 :
Читателю предлагаем найти два других значения корня уравнения х 3 — бх 2 + 20 = 0 из отрезка [2;3] с точностью до 10
Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать
Отделить корни уравнения графически и уточнить один из них методом проб с точностью до 0,001
- Реферат.Справочник
- Контрольные работы по другому
- Отделить корни уравнения графически и уточнить один из них методом проб с точностью до 0,001
Условие
Отделить корни уравнения графически и уточнить один из них методом проб с точностью до 0,001 2ex=3x-1
Ответ
Решение
Отделим корни уравнения графически. Построим графики функций f1(x)=2ex и f2(x)=3x-1
Уравнение не имеет корней, так как два графика не имеют точек пересечения
Изменим исходное уравнение:
2ex=3x+2
Отделим корни уравнения графически . Построим графики функций f1(x)=2ex и f2(x)=3x+2
Уточним корень с отрезка [0,5;1,5]
Метод проб:
Определяем середину отрезка с корнем уравнения и знак функции в нем:
x=a+b2
Далее выбираем ту половину отрезка, на которой знак функции меняется:
если fx*fa 50% текста контрольной работы недоступно
Оплатите контрольную работу или закажите уникальную работу на похожую тему
Видео:Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать
Метод половинного деления. Один из методов уточнения корней уравнения (1) – метод половинного деления
Один из методов уточнения корней уравнения (1) – метод половинного деления. Исходные данные: уравнение f(x)=0; отрезок [a,b], на котором существует единственный корень уравнения (корень отделен), т.е. f(x) удовлетворяет условиям: f(x) непрерывна на [a,b], монотонна нем и f(a)f(b) 0 (знаки функции f(x) в точках a и c одинаковы), то левый конец отрезка заменяется на середину (а=с) иначе правый конец заменяется на середину (b=c).
4. Если длина отрезка не превосходит заданной точности (b-a 4 -x 3 -2x 2 +3x-3=0.
Полагая f(x)= x 4 -x 3 -2x 2 +3x-3, имеем f’(x)=4x 3 -3x 2 -4x+3.
Найдем нули производной: 4x 3 -3x 2 -4x+3=0; 4x(x 2 -1)-3(x 2 -1)=0;(x 2 -1)(4x-3)=0;
Составим таблицу знаков функции f(x):
| x | -∞ | -1 | 3/4 | +∞ | |
| f(x) | + | — | — | — | + |
Из таблицы видно, что уравнение имеет два действительных корня x1 
(-∞;-1) и x2 (1;+ ∞). Уменьшим промежутки, на которых находятся корни, до единичной длины:
| x | -2 | -1 | ||
| f(x) | + | — | — | + |
Следовательно, x1 (-2;-1) и x2 (1;2).
Уточним один из корней, например, x1, методом половинного деления до сотых долей. Все вычисления удобно производить, используя следующую таблицу:
Второй корень, уточняемый аналогичным образом, равен 1,73.
2. Отделить корни графически и уточнить их методом половинного деления.
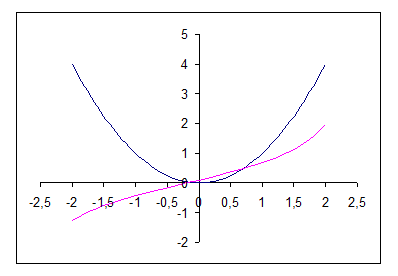
Перепишем уравнение в виде 
. Обозначим 
, 
и построим графики этих функций:
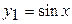
Из рисунка видно, что уравнение имеет три корня: точный x=0 и еще два, расположенных симметрично на отрезках [-3;-2] и [2;3].
Уточним корень на отрезке [2;3]:
Задания
1)Отделить корни аналитически и уточнить их методом половинного деления до 0,01, используя электронные таблицы.
1. 3x 4 +4x 3 -12x 2 -5=0
2. 2x 3 -9x 2 -60x+1=0
5. 3x 4 +3x 3 +6x 2 -10=0
7. x 4 +4x 3 -3x 2 -17=0
8. x 4 -x 3 -2x 2 +3x-3=0
9. 3x 4 +4x 3 -12x 2 +1=0
10. 3x 4 -8x 3 -18x 2 +2=0
11. 2x 4 -3x 3 +8x 2 -1=0
12. 2x 4 +8x 3 +3x 2 -1=0
13. x 4 -4x 3 -8x 2 +1=0
14. 3x 4 +4x 3 -12x 2 -5=0
15. 2x 3 -8x 2 -30x+1=0
17. 2x 4 -2x 2 -7=0
18. 3x 4 +8x 3 +6x 2 -10=0
19. x 4 -18x 2 +6=0
20. x 4 +4x 3 -3x-7=0
21. x 4 -2x 3 -x 2 +3x-3=0
22. 3x 4 +4x 3 -3x 2 -17=0
23. 2x 4 -5x 3 -12x 2 +2=0
24. 3x 4 +9x 3 -14x 2 +1=0
25. x 4 +2x 3 -x-1=0
26. x 4 +8x 3 -6x 2 -72x=0
28. x 4 -3x 2 +75x-10000=0
2) Отделить корни графически и уточнить их методом половинного деления до 0.01, используя электронные таблицы.
Лабораторная работа №3
Решение нелинейных уравнений методом хорд
Краткая теория
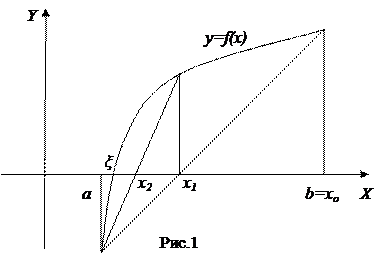
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Уточним этот корень методом хорд. Геометрически метод хорд означает замену на отрезке [a,b] графика функции y=f(x) хордой, проведенной через точки (a,f(a)) и (b,f(b)):
Здесь ξ — точный корень уравнения (1), x 
— начальное приближение к корню, x 
-точка пересечения хорды с осью Ох – первое приближение к корню. Далее метод хорд применяется на отрезке [a, x ] и получается второе приближение к корню — x 
. В случае, изображенном на рис.1, конец отрезка а остается неподвижным. Из уравнения хорды и условия, что точка (x ,0) принадлежит хорде, получается формула для вычисления n-го приближения к корню для случая, когда а – неподвижный конец: x =b,
x 
=a- 
(2)
Для случая неподвижного конца b используется формула: x =a,
x =x 
— 
(3)
Правило определения неподвижного конца хорды:
Если знаки первой и второй производных функции f(x) на отрезке [a, b] совпадают, то неподвижным являются конец b, иначе — конец a.
Метод хорд обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длину n-го отрезка: 
1. Определить, какой конец отрезка будет неподвижным и принять за x другой конец отрезка.
2. Вычислить новое приближение к корню x по формуле (2) или (3).
3. Если длина отрезка [x , x ] не превосходит заданной точности, то процесс заканчивается и в качестве точного корня можно взять x или x , иначе идти к п.2
Решение одного варианта
1.Отделить корни графически и уточнить их методом хорд с точностью до 0.001: tg(0.5x+0.1)=x 
.
Отделим корень графически. Построим графики функций
y =tg(0.5x+0.1) и y =x :
Таким образом, уравнение имеет два корня
x [0.5; 1] и x [-0.5; 0]
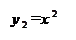
Чтобы уточнить этот корень методом хорд, определим знаки первой и второй производной функции f(x)= tg(0.5x+0.1)-x на промежутке [0.5;1]. Имеем
f ‘(x)=0.5/cos (0.5x+0.1)-2x;
3. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. x lgx — 1.2 = 0
14. 1.8x 2 – sin10x = 0
15. ctgx – x / 4 = 0
16. tg(0.3x + 0.4) = x 2
17. x – 20sinx = 0
18. ctgx – x / 3 = 0
19. tg(0.47x + 0.2) = x 2
20. x 2 + 4sinx = 0
21. ctgx – x / 2 = 0
22. 2x – lgx – 7 = 0
24. 3x – cosx – 1 = 0
26. 10cosx-0,1x 2 =0
2)Отделить корни аналитически и уточнить их методом хорд до 0.001:
💥 Видео
14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать
Метод Ньютона - отделение корнейСкачать
Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать
Найти корень уравнения на заданном интервале (MathCad)Скачать
Метод половинного деления. ДихотомияСкачать
1 3 Решение нелинейных уравнений методом простых итерацийСкачать
Метод касательных (метод Ньютона)Скачать
Числовое решение. Функция root в MathCAD 14 (28/34)Скачать
Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
Как найти корни уравнения в Excel с помощью Подбора параметраСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
1,2 Решение нелинейных уравнений методом хордСкачать
АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать
Численные методы - Занятие 1: Численное решение уравнения методом дихотомииСкачать
Уравнение и его корни | Алгебра 7 класс #16 | ИнфоурокСкачать
7 Метод половинного деления Mathcad Численные методы решения нелинейного уравненияСкачать
Уравнение и его корни. Математика. АлгебраСкачать
