Отделить корни уравнения аналитически и уточнить наибольший корень методом хорд до 0 001

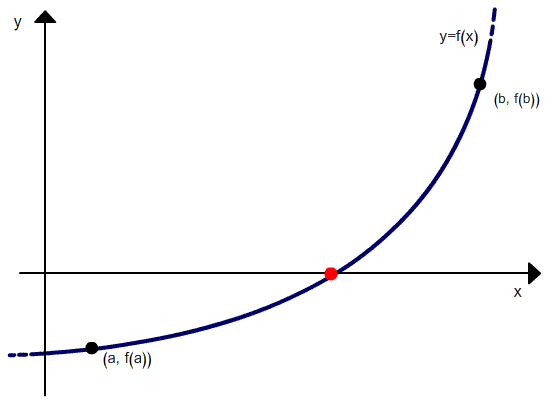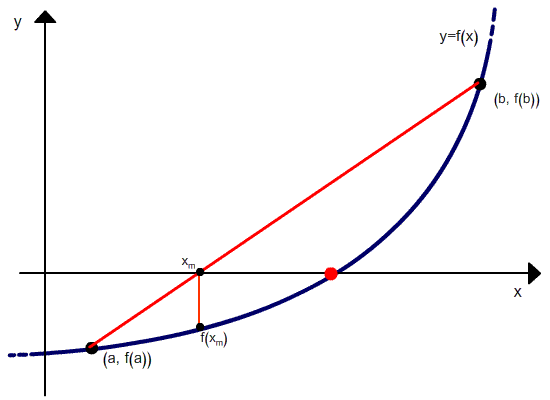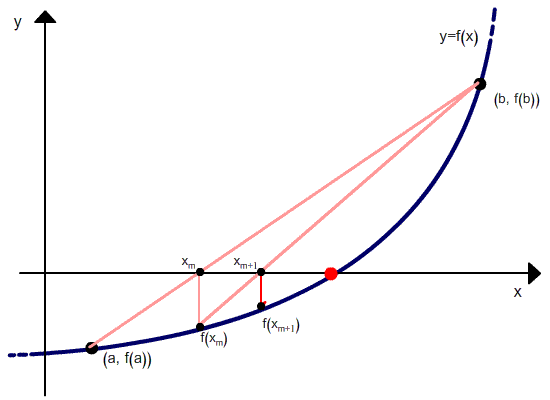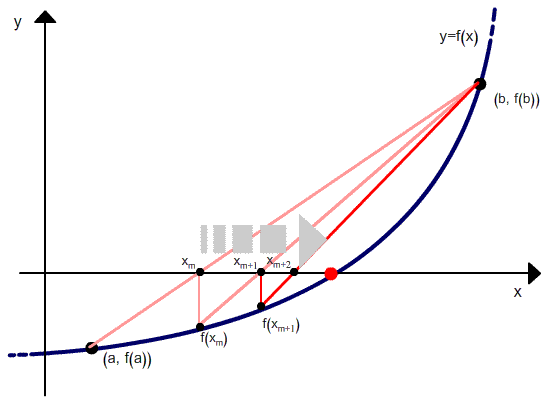
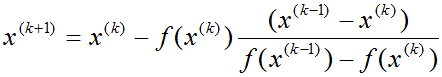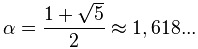Метод хорд — итерационный численный метод приближённого нахождения корня уравнения.

Немного теории о методе хорд под калькулятором.

Метод хорд

Метод хорд

Метод хорд можно рассматривать как комбинацию метода секущих (Метод секущих) и метода дихотомии — отличие от метода секущих состоит в том, что если в методе секущих в качестве точек следующей итерации выбираются последние рассчитанные точки, то в методе хорд выбираются те точки, в которых функция имеет разный знак, и соответственно, выбранный интервал содержит корень.

Вывод итерационной формулы аналогичен выводу формулы для метода секущих:

Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

Для точки пересечения с осью абсцисс (у=0) получим уравнение

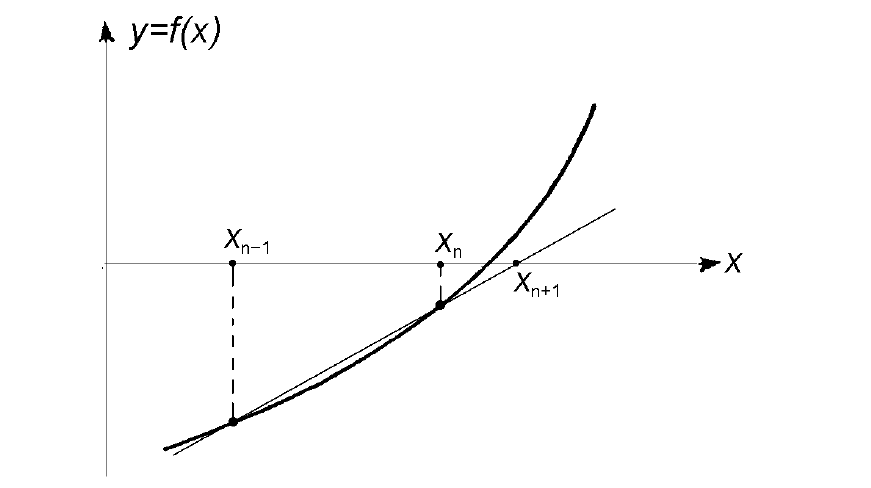
Но в отличие от метода секущих, после расчета следующего приближения в качестве второй точки выбирается не последняя, а та, в которой функция имеет разный знак со значением функции в вычисленной точке. Проиллюстрировано это ниже.

Метод хорд является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале), при этом величина интервала в процессе итераций не стремится к 0.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Программирование на C, C# и Java

Видео:Алгоритмы. Нахождение корней уравнения методом хордСкачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Метод хорд

Метод хорд используется для численного нахождения приближенного значения корня нелинейного уравнения. В данной статье будет показан алгоритм метода, а также будет приведена его программная реализация на языках: Си, C# и Java.

Метод хорд (то же, что метод секущих) — итерационный метод решения нелинейного уравнения.

Нелинейное уравнение — это уравнение в котором есть хотя бы один член, включающий неизвестное, НЕ в первой степени. Обозначается, как: f(x) = 0.

Метод хорд. Алгоритм

Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной.

Итерационная формула для вычислений методом хорд следующая:

Вычисления продолжаются до тех пор, пока не станет истинным выражение:

Геометрическая модель одного шага итераций метода хорд представлена на рисунке:

Метод хорд, в отличие от метода Ньютона, имеет плюс в том, что для расчета не требуется вычисление производных. Но при этом метод хорд медленнее, его сходимость равна золотому сечению:

Метод хорд. Программная реализация

Ниже мы приводим реализацию алгоритма метода хорд на языках программирования Си, C# и Java. Кроме того, исходники программ доступны для скачивания.

В качестве примера ищется корень уравнения x 3 — 18x — 83 = 0 в области x0 = 2, x1 = 10, с погрешностью e = 0.001. (Корень равен: 5.7051).

x_prev — это x_k-1, x_curr — это x_k, x_next — это x_k+1.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Численные методы решения нелинейных уравнений. Метод хорд.

Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Численные методы решения нелинейных уравнений. Метод хорд.

Метод хорд ( метод также известен как Метод секущих ) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения . Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность .

В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось — Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.

Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки и (см. рис.1.).

Рис.1. Построение отрезка (хорды) к функции .

Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид:

Данное уравнение является типовым уравнением для описания прямой вы декартовой системе координат. Наклон кривой задается по ординате и абсциссе с помощью значений в знаменателе и , соответственно.

Для точки пресечения прямой с осью абсцисс записанное выше уравнение перепишется в следующем виде:

В качестве нового интервала для прохождения итерационного процесса выбираем один из двух или , на концах которого функция принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:

или .

Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.

.

Рис.2. Пояснение к определению погрешности расчета.

Следует отметить, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.

Алгоритм нахождения корня нелинейного уравнения по методу хорд

1. Найти начальный интервал неопределенности одним из методов отделения корней. З адать погрешность расчета (малое положительное число ) и начальный шаг итерации ( ) .

2. Найти точку пересечения хорды с осью абсцисс:

3. Необходимо найти значение функции в точках , и . Далее необходимо проверить два условия:

— если выполняется условие , то искомый корень находится внутри левого отрезка положить , ;

— если выполняется условие , то искомый корень находится внутри правого отрезка принять , .

В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:

4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:

— если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:

— если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс и перейти к п.2 рассматриваемого алгоритма.

Видео:Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать

Пример решения уравнений методом хорд

В качестве примера, рассмотрим решение нелинейного уравнения методом хорд. Корень необходимо найти в рассматриваемом диапазоне с точностью .

Вариант решения нелинейного уравнения в программном комплексе MathCAD .

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.1).

Рис.1. Результаты расчета по методу хорд

Для обеспечения заданной точности при поиске уравнения в диапазоне необходимо выполнить 6 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .

Примечание:

Модификацией данного метода является метод ложного положения ( False Position Method ), который отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.

Следует отметить, что в случае если от нелинейной функции можно взять вторую производную алгоритм поиска может быть упрощен. Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:

Случай №1: 0,

f»(a)>0″ width=»158″ height=»20″ border=»0″ />

Из первого условия получается, что неподвижной стороной отрезка является – сторона a .

Случай №2: 0″ width=»158″ height=»20″ border=»0″ />

Из второго условия получается, что неподвижной стороной отрезка является – сторона b .

В общем виде, для выявления неподвижного конца можно записать следующее условие: 0″ width=»122″ height=»20″ border=»0″ /> , где или .

Рис. 3. Примеры убывающей или возрастающей функции

Таким образом, в зависимости от вида функции получаются два выражения для упрощения поиска корня функции:

— если функция соответствует первому случаю (см. рис. 3), тогда формула будет иметь следующий вид:

, где k =0,1,2,…

— если функция соответствует второму случаю (см. рис. 3), тогда формула будет иметь следующий вид:

, где k =0,1,2,…

Случай сводится к рассматриваемому , если уравнение записать в форме: .

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

🎦 Видео

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Метод хордСкачать

1,2 Решение нелинейных уравнений методом хордСкачать

АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

Решение нелинейного уравнения методом хорд (секущих) (программа)Скачать

Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать

Решение нелинейных уравнений методом хордСкачать

Курс по численным методам: Отделение действительных корней алгебраический уравнений | Занятие 1Скачать

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

метод хордСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать