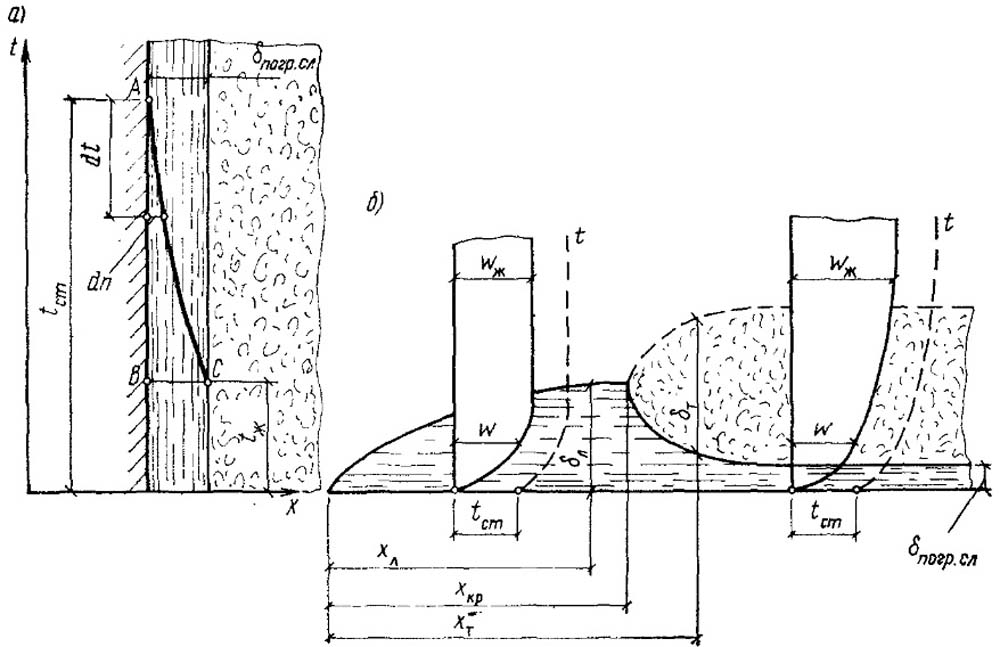
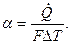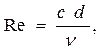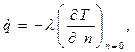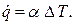От каких факторов зависит величина коэффициента теплоотдачи в уравнении теплопередачи (4 видео)

Основной закон конвективного теплообмена. Коэффициент теплоотдачи и факторы, от которых он зависит

Основной закон конвективного теплообмена – это закон теплоотдачи Ньютона-Рихмана.

Q= 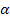(tср-tпов)*F, Вт

tср-tпов— температурный напор,Δt=tср-tпов

F — омываемая площадь.

dQ= (tср-tпов)dF

Формула Ньютона используется одинаковым образом как для задач нагрева поверхности:

t ср>t пов

Так и для задач охлаждения:

Чем выше α — тем выше λ.

Коэффициент температуропроводности учитывает и коэффициент теплопроводности, и плотность самой жидкости.

8. Вязкость жидкости.

Вязкость определяет фомирование как теплового, так и гидродинамического пограничного слоя, и тем самым влияет на α.

9. Фактор теплового характера – это направление теплового потока либо от степенки к жидкости, либо наоборот. В большей мере проявляется в капельных жидкостях.

10.Факторы геометрического характера, т.е. форма, размеры тела и состояние его поверхности.

Содержание

Теплоотдача
Процесс теплоотдачи
Процесс теплоотдачи
📽️ Видео

Видео:3 вида Теплопередачи, которые Нужно ЗнатьСкачать

Теплоотдача

7.1.1.Основной закон теплоотдачи

Понятие конвективного теплообмена охватывает процесс переноса теплоты конвекцией между твердыми поверхностями и омывающими их теплоносителями. Теплоносителем, как правило, является либо жидкость, либо газ. Однако в качестве теплоносителей могут использоваться двух- или трехфазные системы: газ – жидкость; газ – твердые частицы; газ – жидкость – твердые частицы.

В теплоносителе с неоднородным полем температур при вынужденном или естественном перемещении макроскопических элементов наряду с конвекцией происходит процесс переноса тепла теплопроводностью.

Совместный процесс конвекции и теплопроводности называют конвективным теплообменом.

Конвективный теплообмен протекает как внутри теплоносителя, так и на границах его соприкосновения с поверхностями обтекаемых тел.

Конвективный теплообмен между теплоносителем и поверхностью обтекаемого им тела называют теплоотдачей.

Обычно в инженерной практике исследуют теплоотдачу, конвективный же теплообмен внутри теплоносителя при этом не рассматривается.

Тепловой поток при теплоотдаче всегда направлен в сторону меньшей температуры. В процессе теплоотдачи плотность теплового потока, согласно закону Ньютона, прямо пропорциональна температурному напору между теплоносителем и поверхностью теплообмена, т.е.

(7.1)

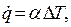
где α – коэффициент пропорциональности, называемый к о э ф ф и ц и е н-

т о м т е п л о о т д а ч и;

∆Т – температурный напор.

Здесь индексом m обозначена температура теплоносителя, индексом cm

– температура поверхности теплообмена (стенки).

Для произвольной поверхности при T_m > T_cm закон Ньютона запишется в виде:

. (7.2)

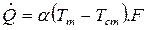
Значения F, T_m и T_cm в уравнении (6.2) не отражают условий теплообмена, влияющих на величину 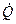. Здесь α не является физической постоянной, присущей данному теплоносителю, а зависит от множества факторов, формирующих картину течения около стенки. По этой причине простота уравнения (7.1) представляется кажущейся, и особенности его использования заключаются в сложности определения коэффициента теплоотдачи.

7.1.2. Факторы, влияющие на коэффициент теплоотдачи.

Величина коэффициента теплоотдачи характеризует интенсивность конвективного теплообмена на границе “теплоноситель-стенка”.

Численно коэффициент теплоотдачи равен тепловому потоку, приходящемуся на единицу поверхности при температурном напоре, равный единице, т.е.

Отсюда же следует и единица α – Вт/(м 2 × К).

Коэффициент теплоотдачи имеет весьма широкий диапазон численных значений, табл. 7.1.

Особенности теплоотдачи	.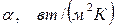
Естественная конвекция газов	6…40
Вынужденное движение газов	12…120
Вынужденное движение пара в трубах	110…2200
Естественная конвекция воды	110…1100
Вынужденное движение воды	500…11000
Пузырьковое кипение воды	8500…18000
Конденсация водяного пара	4500…22000

На величину коэффициента теплоотдачи влияют, прежде всего, теплофизические свойства теплоносителя, его фазовое состояние, вид движения (естественное или вынужденное) и режим течения теплоносителя. Различают ламинарный, переходный и турбулентный режимы течения.

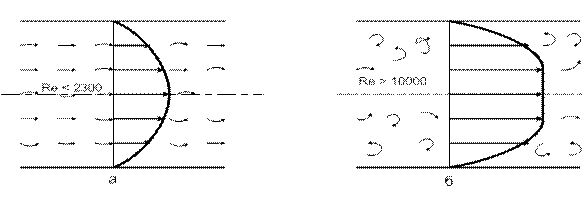
При ламинарном (слоистом) режиме макрочастицы жидкости движутся, не перемешиваясь, параллельно омываемым стенкам и траекториям других частиц. В силу внутреннего трения скорость теплоносителя переменна по сечению нормальному к поверхности. Так, для канала круглого сечения эпюра скорости имеет параболическую форму, рис.7.1, а Перенос тепла при ламинарном режиме движения происходит в осноном за счет теплопроводности теплоносителя и естественной конвекции.

При турбулентном режиме макрочастицы перемещаются по сложным траекториям, не совпадающим с общим направлением потока. Их движение неупорядоченное, хаотичное. Эпюра скорости имеет вид усеченной параболы, (см. рис. 7.1, б). Теплоотдача при турбулентном режиме течения теплоносителя отличается несравненно большей интенсивностью, чем при ламинарном режиме

Как при ламинарном, так и при турбулентном режимах движения скорость теплоносителя непосредственно на стенке равна нулю, а с увели -чением расстояния по нормали от стенки она возрастает.

Слой теплоносителя около поверхности тела, где скорость изменяется от нуля до величины, примерно равной 0,9 скорости невозмущенного потока, называют г и д р о д и н а м и ч е с к и м пограничным слоем и обозначают буквой δ_{д ,} рис.7.2.

Кроме того, необходимо отметить, что в турбулентном пограничном слое непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Этот слой называют вязким, или л а м и н а р н ы м п о д с л о е м и обозначают δ_л (см. рис. 7.2, б).

Если температуры стенки и теплоносителя не одинаковы, то вблизи стенки образуется тепловой пограничный слой δ_т (см. рис.7.2, в). В нем температура изменяется от T_cm до ≈ T_m , т.е. все изменение температуры происходит в сравнительно тонком слое, непосредственно прилегающем к поверхности теплоотдачи. Значения толщин δ_д и δ_т в общем случае не равны, соотношение между ними зависит от рода жидкости. Однако изменения в δ_д приводят к изменениям δ_т. С увеличением скорости теплоносителя значения толщин δ_д , δ_т и δ_л уменьшаются.

При вынужденной конвекции режим течения оценивают по безразмерному комплексу, называемому критерием Рейнольдса. Для цилиндрического канала критерий Рейнольдса имеет вид:

где c — скорость течения теплоносителя,;

d — диаметр канала,;

ν — коэффициент кинематической вязкости,.

Течение теплоносителя в трубах принято считать ламинарным до

Re Re 10000 течение турбулентное.

Для того, чтобы качественно оценить влияние режима течения теплоносителя на коэффициент теплоотдачи, запишем уравнение теплоотдачи в дифференциальной форме.

Для слоя теплоносителя непосредственно на поверхности теплообмена по закону Фурье следует:

где n – нормаль к поверхности тела,.

С другой стороны, согласно закону Ньютона,

Приравнивая правые части этих уравнений, получим:

(7.3)

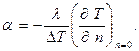
Уравнение (7.3) выражает условия теплоотдачи на границе “твердая стенка – теплоноситель”.

Чем больше скорость движения теплоносителя, тем меньше толщина пограничного слоя, тем больше градиент температуры и, следовательно, больше коэффициент теплоотдачи. Через толщину пограничного слоя на 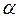влияют форма и размер поверхности теплообмена.

Величина коэффициента теплоотдачи зависит от физических свойств теплоносителя.С увеличением плотностиρ, теплопроводности λ, теплоем-кости c_pи уменьшением вязкости ν коэффициент теплоотдачи возрастает.

Влияние температур T_m и T_cm на 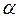сказывается через их воздействие на физические свойства теплоносителя.

Таким образом, в самом общем виде коэффициент теплоотдачи является функцией многих факторов:

где X – характер движения теплоносителя;

Ф – форма поверхности теплообмена;

l – характерный геометрический размер;

c – скорость движения теплоносителя.

Для определения коэффициента теплоотдачи в зависимости от поста-

новки задачи могут использоваться следующие методы: экспериментальный,

аналитический и метод теплового подобия.

Чисто экспериментальный метод определения коэффициента теплоотдачи весьма прост и достоверен, так как требует опытного измерения

только трех величин: , T_m и T_cm. Отсюда

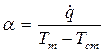
Этот метод широко используется при исследовании влияния различных факторов на интенсивность теплоотдачи в функционирующих теплообменных установках. Однако экспериментальный метод имеет существенный недостаток, состоящий в том, что полученное значение α не может быть рекомендовано для использования при расчетах устройства, характеристики которого хотя бы незначительно отличаются от характеристик опытной установки.

Аналитические методы основаны на теории пограничного слоя. Сущность этих методов состоит в составлении замкнутой системы дифференциальных уравнений, описывающих процесс конвективного теплообмена в движущемся теплоносителе и последующем решении этой системы. Дифференциальные уравнения, описывающие конвективный теплообмен, устанавливают самую общую связь между величинами, характерными для этого процесса. Следовательно, эти дифференциальные уравнения являются математической моделью целого класса процессов теплообмена. Для получения частного решения эти уравнения дополняются условиями однозначности.

В большинстве случаев, из-за сложности математического описания профиля скорости в пограничном слое, решения, удовлетворяющие дифференциальным уравнениям и условиям однозначности, весьма трудоемки.

Следовательно, если недостатком экспериментального метода определения α является невозможность распространения результатов опытов на другие условия теплообмена, отличающиеся от изученного, то недостатком аналитического метода является невозможность перейти от класса явлений конвективного теплообмена, характеризующегося дифференциальными уравнениями, к единичному, конкретному явлению. Каждый из этих методов в отдельности не может быть эффективно использован для решения практических задач.

В настоящее время для определения коэффициента теплоотдачи в основном используется метод теплового подобия, который объединяет в себе положительные стороны экспериментального и аналитического методов.

Видео:Теплопередача. Виды теплопередачи | Физика 8 класс #2 | ИнфоурокСкачать

Процесс теплоотдачи

Процесс теплообмена между жидкостью и стенкой, которую эта жидкость омывает, называется конвективным теплообменом, или процессом теплоотдачи. Процесс теплоотдачи предполагает, что теплота передается одновременно путем теплопроводности и конвекции, и поэтому такой вид теплообмена представляет собой сложный процесс, зависящий от большего числа факторов по сравнению с процессом чистой теплопроводности.

Конвективный теплообмен характерен для большинства процессов тепловой обработки строительных материалов и изделий, связанных с прохождением газов через слой материала, через садку изделий, над уровнями жидкостей при сушке и т. д.

Факторы, влияющие на процесс теплоотдачи, условно можно разделить на следующие группы.

I. Природа возникновения движения жидкости вдоль стенки. В зависимости от причины, вызывающей движение жидкости, различают два вида движения — свободное и вынужденное. Свободное движение, называемое иначе естественной конвекцией, вызывается подъемной силой, обусловленной разностью плотностей холодных и нагретых частиц жидкости. Интенсивность свободного движения зависит от вида жидкости, разности температур между отдельными ее частицами и объема пространства, в котором протекает процесс.

Вынужденное движение жидкости, или вынужденная конвекция, обусловлено работой внешних агрегатов (насоса, вентилятора и т. п.). Движущая сила при этом виде движения возникает вследствие разности давлений, устанавливающихся на входе и выходе из канала, по которому перемещается жидкость. Если скорость вынужденного движения небольшая и есть разница температур между отдельными частицами жидкости, то наряду с вынужденным движением может наблюдаться и свободное движение.

II. Режим движения жидкости. Движение жидкости может иметь ламинарный или турбулентный характер. В первом случае частицы жидкости в форме отдельных несмешивающихся струй следуют очертаниям канала или стенки и профиль скоростей на достаточном удалении от начала трубы имеет вид правильной параболы. Подобное распределение установившихся скоростей обусловливается наличием сил внутреннего трения (вязкости) между частицами жидкости. При этом максимальная скорость движения частиц жидкости, перемещающейся по оси трубы, в 2 раза больше средней скорости их движения, получаемой в результате деления секундного объема жидкости на площадь поперечного сечения трубы (рис. 14.1, а).

Турбулентный режим движения характеризуется непостоянством скорости движения частиц жидкости в рассматриваемой точке пространства. Из — за непрерывного перемешивания жидкости в ней нельзя выделить отдельные струи, и такое движение лишь условно можно назвать стационарным, считая для каждой частицы жидкости характерными не мгновенные, а усредненные за некоторый промежуток времени значения скорости. В этом случае профиль скоростей по сечению трубы будет иметь вид усеченной параболы и максимальная скорость, наблюдаемая у частиц жидкости, движущихся по оси трубы, будет всего в 1,2 — 1,3 раза больше средней скорости. Характерно, что не все частицы жидкости при турбулентном режиме имеют неупорядоченное движение. Вблизи стенок, ограничивающих потоки, вследствие вязкости жидкости пульсации скорости уменьшаются, и около самой стенки сохраняется тонкий пограничный слой, движущийся ламинарно.

В пределах этого слоя, который имеет толщину не более нескольких тысячных долей диаметра трубы, скорость движения частиц жидкости резко меняется от нуля на самой стенке до 0,4 — 0,7 средней скорости на условной границе с турбулентным ядром потока (рис. 14.1, б).

Строго говоря, турбулентные пульсации проникают и в ламинарный подслой и затухают в нем вследствие действия сил вязкости. Поэтому термин «ламинарный подслой» правильнее заменять термином «вязкий подслой».

Английский физик Рейнольдс установил, что при движении жидкости в трубах переход из ламинарного режима в турбулентный определяется значением безразмерного комплекса wdp/µ, в который входят средняя скорость w, диаметр трубы d, плотность р и динамическая вязкость жидкости µ. Этот комплекс называют числом Рейнольдса и обозначают символом Re. При Re ≤ 2300 движение жидкости в трубах имеет ламинарный характер, а при Re ≥ 10 000 — турбулентный, т. е. критическая скорость, позволяющая определить переход любой жидкости из ламинарного режима в турбулентный для трубы любого диаметра, может быть найдена из соотношения w_кр — 2300 µ /pd.

В большинстве случаев, встречающихся в теплотехнике, Re > 10 000 и движение оказывается турбулентным. В особых условиях (при отсутствии шероховатостей на стенках, безвихревом входе жидкости в трубу и т. п.) можно сохранить ламинарное движение при числах Re до 10 000, но такое движение весьма неустойчиво и при небольшом местном возмущении потока из ламинарного сразу переходит в турбулентное. Показанные на рис. 14.1 кривые, характеризующие закономерность распределения скоростей по сечению трубы, справедливы лишь для стабилизированного движения. На основании опытных данных длина участка стабилизации для ламинарного режима может быть принята 0,03 d Re, а для турбулентного режима — около 40 d.

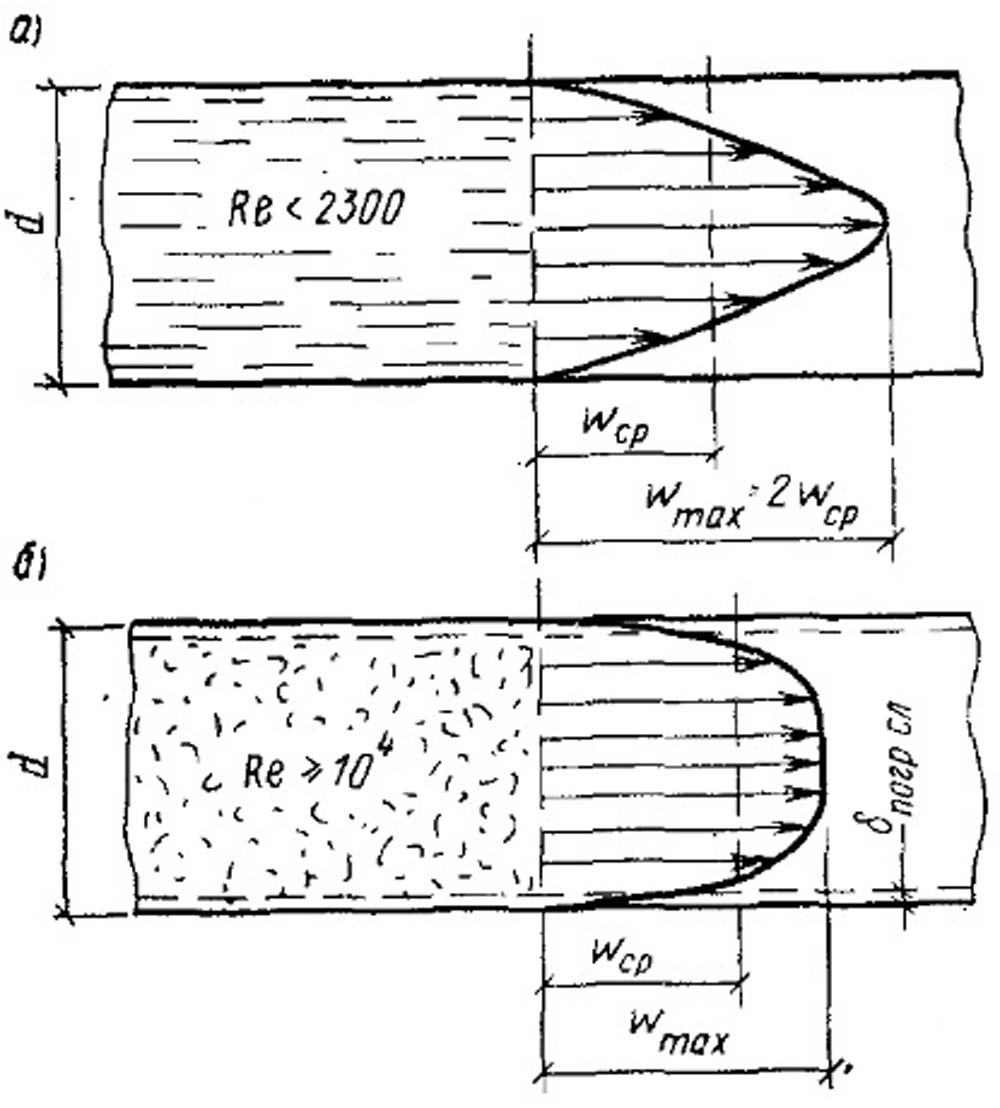
Режим движения жидкости определяет механизм переноса теплоты в процессе теплоотдачи. При ламинарном движении перенос теплоты от жидкости к стенке (или наоборот) осуществляется главным образом путем теплопроводности. При турбулентном движении такой способ передачи теплоты наблюдается лишь в ламинарном пограничном слое, а внутри турбулентного ядра теплота переносится путем конвекции. При этом на интенсивность теплоотдачи в основном влияет термическое сопротивление пограничного слоя. Последнее наглядно иллюстрируется рис. 14.2, на котором представлена схема движения жидкости при обтекании плоской поверхности (пластины).

Следует отметить, что по мере движения потока вдоль поверхности стенки толщина пограничного слоя постепенно возрастает тормозящее воздействие стенки распространяется на все более далекие слои жидкости. На небольших расстояниях от передней кромки стенки пограничный слой еще тонкий и течение жидкости в нем носит струйный ламинарный характер. Далее на некотором расстоянии х_кр в пограничном слое начинают возникать вихри и характер течения становится турбулентным (рис. 14.2,б) Эти вихри обеспечивают интенсивное перемешивание жидкости в пограничном слое, но в непосредственной, близости от поверхности стенки они затухают, и здесь сохраняется очень тонкий вязкий подслой. Толщина пограничного слоя б _{погр.сл} зависит от расстояния х от передней кромки стенки, скорости движения потока и кинематической вязкости v = µ /р. Переход к турбулентному режиму течения жидкости в пограничном слое определяется критическим значением числа Re_кp, на которое при продольном обтекании пластины основное влияние оказывают степень начальной турбулентности набегающего потока жидкости, а также шероховатость поверхности, интенсивность теплообмена поверхности с жидкостью и т. д. Поскольку сам переход от ламинарного режима течения к турбулентному в пограничном слое происходит не в точке, а на некотором участие, вводят два критических значения числа Рейнольдса. При этом Re_кp1 соответствует превращению ламинарного режима течения в переходный. В это время в пограничном слое начинают возникать первые вихри и пульсации, а Re_кр2 соответствует переходу к развитому турбулентному режиму течения.

Следует также отметить, что наряду с описанным процессом формирования гидродинамического пограничного слоя происходит аналогичный процесс формирования и теплового пограничного слоя, в пределах которого температура меняется от t_ст до t_ж. Характер распределения температуры в тепловом пограничном слое зависит от режима течения жидкости в динамическом пограничном слое.

При ламинарном течении перенос теплоты между слоями жидкости осуществляется путем теплопроводности. В турбулентном пограничном слое основное изменение температуры происходит в пределах тонкого вязкого подслоя около стенки, через который теплота также передается путем теплопроводности. В турбулентном ядре пограничного слоя вследствие интенсивного перемешивания жидкости температура изменяется незначительно (см.рис. 14.2, б) и поле температур имеет ровный пологий характер, т. е. отмечается качественное сходство в пограничном слое между распределением температур и скоростей.

III.Физические свойства жидкостей. На процесс теплоотдачи непосредственно влияют следующие физические параметры жидкостей: теплопроводность µ, удельная теплоемкость с, плотность р, а также вязкость и температуропроводность.

Рис. 14.1. Распределение скоростей по сечению трубы при ламинарном (а) и турбулентном (б) режимах.

Рис. 14.2. Характер изменения температуры в пограничном слое (а) и скорости в тепловом и динамическом пограничных слоях (б) б_л, б_т — толщина пограничного слоя соответственно ламинарного и турбулентного.

Известно, что все жидкости обладают вязкостью, т. е. между отдельными частицами или слоями, перемещающимися с различными скоростями, всегда возникает сила внутреннего трения, противодействующая движению. По закону Ньютона, эта сила F, отнесенная к единице поверхности, пропорциональна градиенту скорости dw/dn, т. е. F = µdw/dn.

Коэффициент пропорциональности µ, в этом уравнении называется коэффициентом внутреннего трения или динамической вязкостью. При dw/dn = 1, µ = F, т. е. динамическая вязкость численно равна силе трения, приходящейся на единицу поверхности соприкосновения двух слоев жидкости, скользящих один по другому, при условии, что на единицу длины нормали к поверхности скольжения скорость движения изменяется на единицу. Отношение µ /p = v называется кинематической вязкостью. Если в комплексе wdp/µ заменить отношение р/µ = 1/v, то число Рейнольдса принимает вид Re = wd/v.

Понятие температуропроводности тел связано с протеканием в них нестационарных тепловых процессов, наблюдаемых обычно при нагревании или охлаждении. Скорость теплового процесса при нестационарном режиме определяется отношением µ/ср = а, которое называется температуропроводностью. Температуропроводность характеризует скорость выравнивания температуры в различных точках тела. Чем больше величина а, тем быстрее все точки какого-либо тела при его остывании или нагревании достигнут одинаковой температуры.

Единицей измерения динамической (абсолютной) вязкости µ. служит Па — с, а единицей измерения v и а — м 2 /с.

IV.Форма, размеры и состояние поверхности стенки, омываемой жидкостью. Обычно поверхности стенок имеют форму плит или труб, которые могут располагаться вертикально, горизонтально или наклонно. Каждая из этих форм поверхностей создает специфические условия для теплообмена между поверхностью стенки и жидкостью, омывающей эту поверхность. Для процесса теплоотдачи очень важно, перемещается ли жидкость внутри замкнутого пространства или поверхность стенки со всех сторон омывается жидкостью.Большое значение имеет также состояние поверхности стенки, оцениваемое ее шероховатостью.

Из рассмотрения факторов, влияющих на процесс теплоотдачи, видно, насколько сложно определить количество теплоты, переданной при конвективном теплообмене. Поскольку интенсивность процесса теплоотдачи в основном определяется наличием и толщиной ламинарного пограничного слоя, через который теплота передается лишь путем теплопроводности, для решения указанной задачи можно было бы воспользоваться законом Фурье, написав его в виде следующего уравнения:

(14.1)

Однако для расчетов использовать это уравнение не представляется возможным, так как значение температурного градиента у стенки grad ts и его изменение по всей поверхности теплообмена S определить не удается.

Для удобства расчетов в соответствии с рис. 14.2, а значение градиента температуры dt/dn из подобия элементарного треугольника и треугольника ABC заменяют отношением:

(14.2)

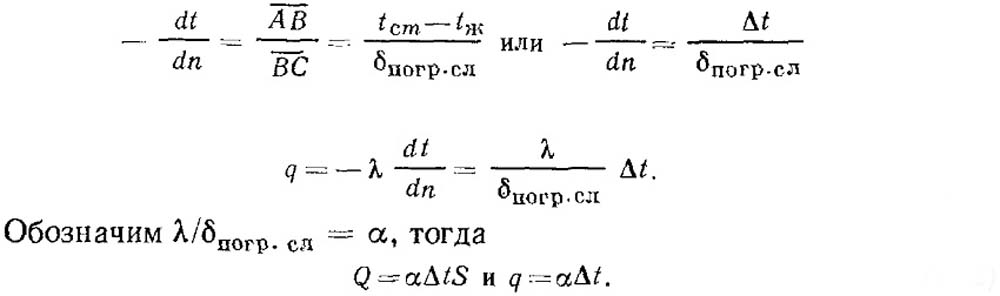
Это уравнение в теплотехнике называется уравнением Ньютона.

В формуле (14.2) Δt — температурный напор, а коэффициент пропорциональности α, характеризующий условия теплообмена между жидкостью и поверхностью твердого тела называется коэффициентом теплоотдачи (теплообмена) Единицей измерения для α служит Вт/(м 2 ×К).

Числовое значение коэффициента теплоотдачи определяет мощность теплового потока, проходящего от жидкости к стенке (или обратно) через единицу поверхности (1 м 2 ) при разности температур между жидкостью и стенкой 1°.

Коэффициент теплоотдачи α зависит от большого числа разнообразных факторов, указанных в перечисленных четырех группах. Это приводит к тому, что при одинаковых условиях процесса теплоотдачи значения α колеблются в весьма широких пределах, Вт/(м 2 ×К), например:

Следует отметить, что с возрастанием вязкости повышается толщина пограничного слоя и уменьшается коэффициента возрастание скорости потока теплоносителя приводит к уменьшению толщины пограничного слоя и к увеличению коэффициента теплоотдачи.

Наиболее точно коэффициент теплоотдачи а можно определить опытным путем. Но этот способ определения а представляет собой нелегкую задачу, особенно для сложных и громоздких тепловых устройств, например таких, как паровой котел. Но и проводя опыты, нельзя быть уверенным в том, что закономерности, найденные для данного теплового агрегата, окажутся справедливыми для другого аппарата, может быть еще не построенного и потому недоступного для непосредственного изучения.

В настоящее время опытное определение коэффициента теплоотдачи производится, как правило, не на самих образцах тепловых устройств, а на их упрощенных моделях, более удобных для экспериментирования. Результаты опытов, проведенных на моделях, обобщают, используя тепловую теорию подобия (см. § 14.3). Основной вывод, который делают на основе этой теории, заключается в том, что нет необходимости искать зависимость коэффициента теплоотдачи от каждого из тех факторов, которые на него влияют, а достаточно найти зависимость между определенными безразмерными комплексами величин, характерных для рассматриваемых условий процесса теплоотдачи. Эти безразмерные комплексы величин называют критериями подобия. Составленные из размерных величин критерии подобия отражают физическую сущность, или, как говорят, модель процесса. Следовательно, задача заключается в том, чтобы найти вид зависимостей между критериями подобия, называемых критериальными уравнениями. Составляют критерии подобия с помощью дифференциальных уравнений конвективного теплообмена, т. е. уравнений, которые дают аналитическую зависимость между параметрами, характеризующими процесс теплоотдачи в дифференциальной форме.