От чего зависит направление ветвей параболы являющейся графиком квадратного уравнения y ax2 bx c (2 видео)

Содержание

Квадратичная функция. Построение параболы
Основные понятия
Построение квадратичной функции
Алгоритм построения параболы
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Парабола, график, вершина, нули.
теория по математике 📈 функции
Пример №1
Пример №2
Пример №3
Пример №4
График квадратного трёхчлена
График функции y = ax²
График функции y = ax²+c
График функции y = a(x+d)²
График квадратного трёхчлена y = ax²+bx+c
🎬 Видео

Видео:Построение графика квадратичной функции y=ax²+bx+cСкачать

Квадратичная функция. Построение параболы

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:

Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ: наглядно.

Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 в частном случае при b = 0, c = 0:

Точки, обозначенные фиолетовыми кружками, называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
Если старший коэффициент меньше нуля (a 2 + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

Если D 0,то график выглядит так:

Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Видео:КВАДРАТИЧНАЯ ФУНКЦИЯ y=ax2+bx+c свойства и график квадратичной функцииСкачать

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Видео:Квадратичная функция за 5 минутСкачать

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.

Нанесем эти точки на координатную плоскость и построим график параболы:

Видео:Парабола. Квадратичная функцияСкачать

**Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀**

Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x₀) + y₀, где x₀, y₀ — координаты вершины параболы.

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

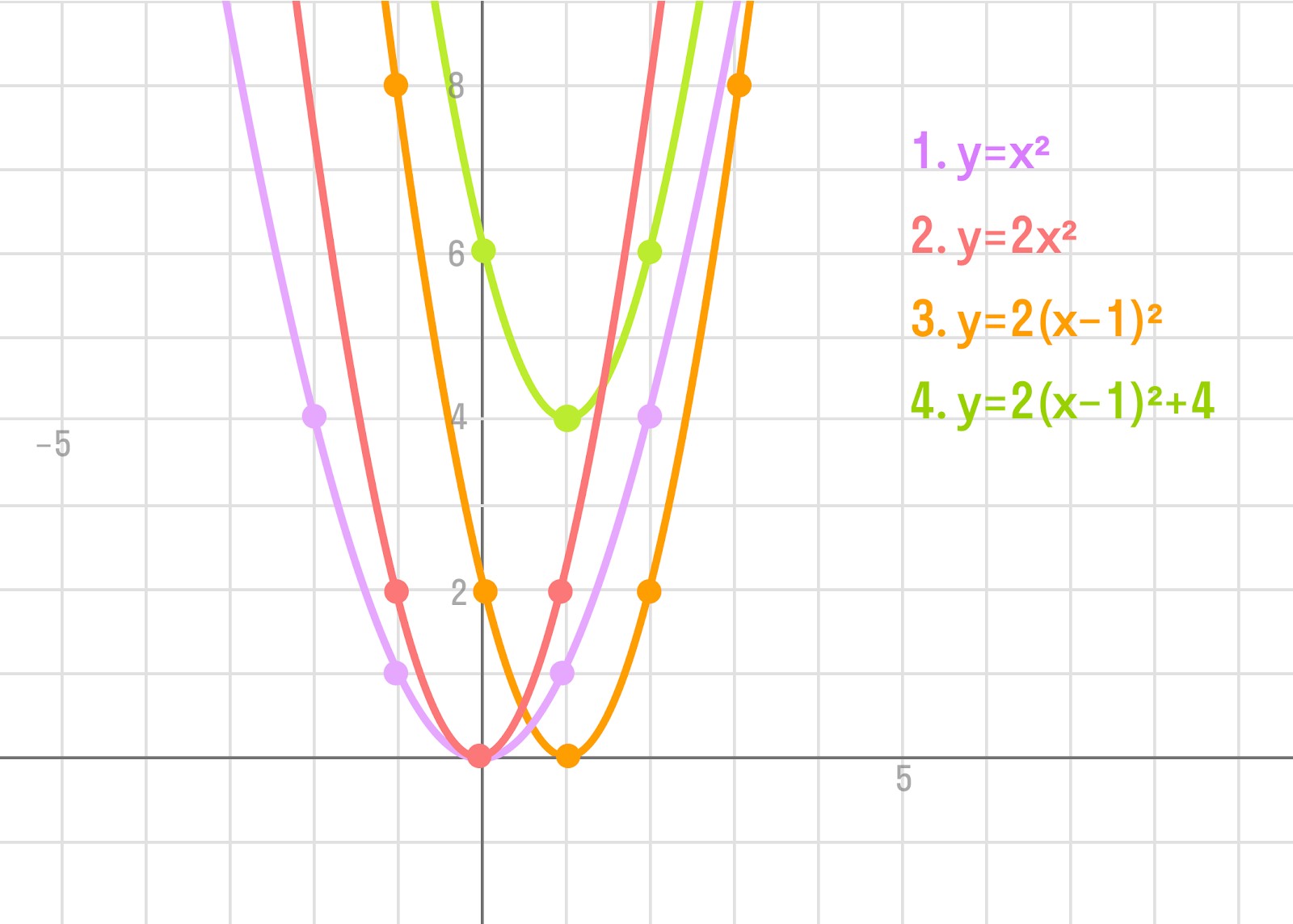
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

построить график функции y = x 2 ,
умножить ординаты всех точек графика на 2,
сдвинуть его вдоль оси ОХ на 1 единицу вправо,
сдвинуть его вдоль оси OY на 4 единицы вверх.

Построить график параболы для каждого случая.

Видео:Квадратичная функция и ее график. 8 класс.Скачать

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид функции позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.

Отметим эти точки на координатной плоскости и соединим плавной прямой линией.

Видео:Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Парабола, график, вершина, нули.

теория по математике 📈 функции

Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.

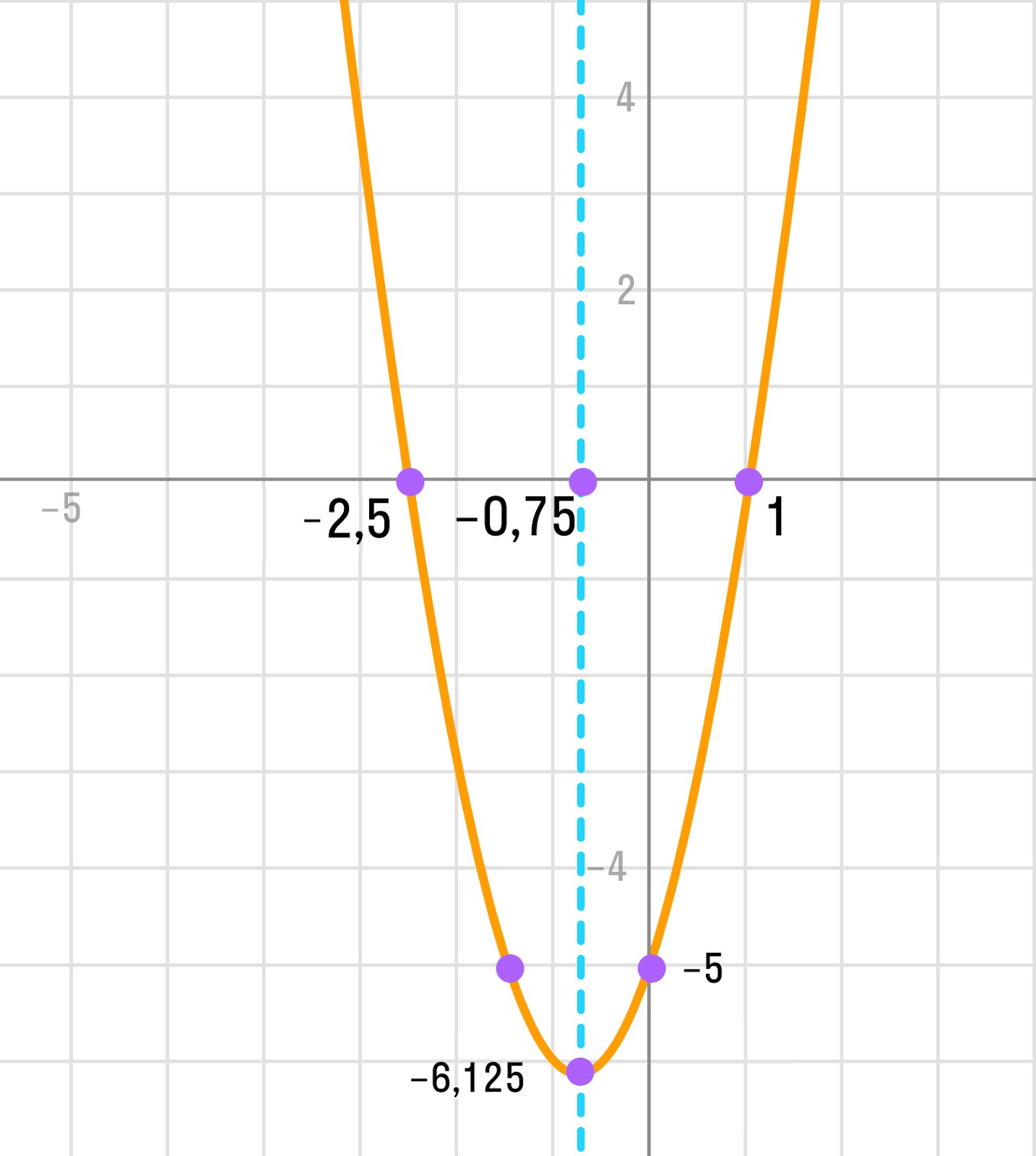
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Чтобы найти координаты вершины параболы (х₀; у₀), надо воспользоваться формулой:

для нахождения у₀ можно просто подставить значение х₀ в формулу данной функции y₀=ax 2 +bx+c вместо х.

Рассмотрим это на примере конкретно заданной функции.

Пример №1

Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.

Найдем, чему равны коэффициенты: а=2; b= – 8

Подставим их в формулу и вычислим значение х₀:

х₀= − b 2 a . . = 8 2 ∙ 2 . . = 8 4 . . = 2

Теперь в заданную по условию формулу вместо х подставим найденное значение у₀=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3

Итак, мы нашли координаты вершины параболы: (2; –3).

Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.

Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.

Пример №2

Найти нули функции у=х 2 +4х – 5

Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:

D=b 2 – 4ac=4 2 – 4 ∙ 1 ∙ ( − 5 ) = 36

Значит, нули функции равны –5 и 1

Примечание к заданию по нахождению нулей функции без графика

Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).

Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.

Пример №3

Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:

А	Б	В
2	3	1

Пример №4

Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х₀.

Итак, найдем х₀ для формулы «Б»:

х₀= − b 2 a . . = − 4 2 ∙ 2 . . = − 4 4 . . = − 1

Видим, что х₀ отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.

Запишем в таблицу

А	Б	В
2	3	1

А) a>0, с >0 Б) а 0 В) а>0, с

На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 – это график №1

Б) а 0 – это график №3

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

ФУНКЦИИ

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.

Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3

pазбирался: Даниил Романович | обсудить разбор | оценить

На рисунках изображены графики функций вида

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида

Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

Из всего вышеперечисленного можно найти ответ:

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Занятие 2. График параболы y=ax^2+bx+cСкачать

График квадратного трёхчлена

График функции y = ax²

Начертим на одном чертеже два графика:

График с «минусом» — это та же парабола, только направленная ветками вниз, с вершиной в начале координат.

Обе параболы взаимно симметричны относительно оси OX.

Начертим на одном чертеже три графика:

$$ y = x^2, y = 2x^2, y = frac x^2 $$

Свойства графика y = ax²

1. При любом a графиком функции $y = ax^2$ является парабола, с осью симметрии OY.

2. Если $a gt 0$, ветки параболы $y = ax^2$ направлены вверх, точка минимума находится в начале координат; при $x lt 0$ функция убывает, при $x gt 0$ функция возрастает.

Если $a lt 0$, ветки параболы $y = ax^2$ направлены вниз, точка максимума находится в начале координат; при $x lt 0$ функция возрастает, при $x gt 0$ функция убывает.

3. Если $a gt 1$, парабола $y = ax^2$ быстрее уходит на бесконечность, чем $y = x^2$, её ветки расположены ближе к оси Y. Чем больше параметр a, тем больше сужаются ветки.

Если $0 lt a lt 1$, парабола $y = ax^2$ медленней уходит на бесконечность, чем $y=x^2$, её ветки расположены дальше от оси Y. Чем меньше параметр a, тем больше расходятся ветки от оси OY.

4. Для отрицательных значений $a lt 0$ ветки сужаются или расходятся аналогично.

График функции y = ax²+c

Начертим на одном чертеже три графика:

$$ y = x^2, y = x^2+2, y = x^2-2 $$

Прибавление двойки поднимает каждую точку исходного графика $y = x^2$ на 2 единицы вверх.

Вычитание двойки – опускает каждую точку на 2 единицы вниз.

Координаты вершины параболы $y = ax^2+c$ в общем случае: (0;c)

Свойства графика y = ax²+c

График $y = ax^2+c$ наследует все свойства графика y=ax² с той разницей, что вершина параболы теперь находится не в начале координат, а в точке (0;c) на оси OY.

График функции y = a(x+d)²

Начертим на одном чертеже три графика: $y = x^2, y = (x+2)^2, y = (x-2)^2$

Прибавление двойки перед возведением в квадрат сдвигает исходный график $y = x^2$ на две единицы влево. Вычитание двойки – на две единицы вправо.

В общем случае у параболы $y = a(x+d)^2$ координаты вершины (–d;0).

Свойства графика y = a(x+d)²

График $y = a(x+d)^2$ наследует все свойства графика $y = ax^2$ с той разницей, что вершина параболы теперь находится не в начале координат, а в точке (-d;0) на оси OX.

График квадратного трёхчлена y = ax²+bx+c

Чтобы проследить перемещение вершины графика $y = ax^2+bx+c$ по сравнению с параболой $y = ax^2$, перепишем квадратный трёхчлен в таком виде:

Учитывая, что $D = b^2-4ac$, получаем:

Разберём полученный результат.

Как мы уже знаем, параметр a отвечает за направление веток параболы ($a gt 0$ — ветки вверх, $a lt 0$ – ветки вниз). Также, параметр a отвечает за сужение или расширение параболы ($|a| gt 1$ — парабола сужается, $|a| lt 1$ — парабола расширяется).

Слагаемое $ frac$ в скобке $left(frac right)^2$ сдвигает вершину параболы влево.

Слагаемое $(-frac)$ опускает вершину параболы вниз.

График квадратного трёхчлена $ y = ax^2+bx+c$ — это парабола с вершиной в точке:

Если $a gt 0$ , то ветви параболы направлены вверх, и в вершине – минимум.

Если $a lt 0$ , то ветви параболы направлены вниз, и в вершине – максимум.

Ось симметрии параболы: $x = -frac$ – прямая, параллельная оси OY.