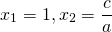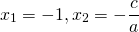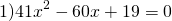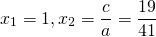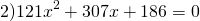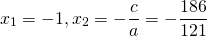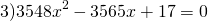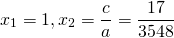Особые случаи в квадратных уравнениях (3 видео)

Особые случаи решения квадратных уравнений.

Решение квадратного уравнения со вторым чётным

коэффициентом при неизвестном.

х2+ bх+ c = 0

D = (2k) 2 – 4ac = 4k 2 – 4ac = 4 ∙ (k 2 – ac) = 4D₁, где D₁ = k 2 – ac.

Содержание

Просмотр содержимого документа «Особые случаи решения квадратных уравнений.»
Узнать ещё
Как решать квадратные уравнения? Особые случаи.
Частные случаи нахождения корней квадратного уравнения
🔥 Видео

Просмотр содержимого документа
«Особые случаи решения квадратных уравнений.»

МБОУ «Койинская СОШ».

Выполнила ученица 8 класса Бекушева Татьяна

под руководством Рогозиной А.М.

Решение квадратного уравнения со вторым чётным

коэффициентом при неизвестном.

b = 2k = k =

ax 2 + 2kx + c = 0

D = (2k) 2 – 4ac = 4k 2 – 4ac = 4 ∙ (k 2 – ac) = 4D₁, где D₁ = k 2 – ac.

Х_{1, 2} = =

9х 2 – 14х + 5 = 0, ответ: х₁ = ; х₂ = 1.

4х 2 + 4х + 1 = 0, ответ: х₁ = — .

7х 2 – 20х + 14 = 0, ответ: х_1,2 = .

Если в квадратном уравнении ах 2 + вх + с = 0, а + в + с = 0, то х₁ = , х₂ = 1.

= = =

D = в 2 — 4а∙(-(а + в)) = в 2 + 4а 2 + 4ав = (в + 2а) 2 0 =

Х₁ = = , т.к. с = — в – а из равенства а + в + с = 0.

Если а+в=с=0 в уравнении ах 2 +вх+с=0, то

х₁=; х₂=1

Видео:Быстрый способ решения квадратного уравненияСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Как решать квадратные уравнения? Особые случаи.

Как быстро решать квадратные уравнения? Эта задача легко разрешима для особых случаев: a+b+c=0 и a-b+c=0.

1) Если a+b+c=0, то

2) Если a-b+c=0, то

Этот способ особенно удобен для не приведенных квадратных уравнений. Рассмотрим примеры.

Особенно актуален данный способ при решении квадратных уравнений с большими коэффициентами.

Видео:Частные случаи решения квадратных уравненийСкачать

Частные случаи нахождения корней квадратного уравнения

Разделы: Математика

Цели урока:

Закрепить умения устно находить корни квадратного трехчлена по теореме Виета; познакомить с частными случаями нахождения корней квадратного уравнения, раскрыть связи между корнями квадратного уравнения и его коэффициентами.
Активизировать творческую и мыслительную деятельность учащихся, способствовать выработке у школьников умения обобщать изучаемые факты; развивать исследовательские навыки и самостоятельность.
Воспитывать умение использовать замеченные свойства изучаемых объектов для решения задач, умение их обобщать, расширить кругозор.

Метод обучения: беседа, объяснение, письменные и устные упражнения.
Форма контроля: самостоятельная работа.

Ход урока.

1. Организационный момент.

2. Актуализация прежних знаний.

Вопросы:

Какие виды квадратных уравнений вы знаете?
Дайте определение квадратного уравнения.
Как называются числа a, b и c ?
Можно ли назвать квадратными уравнения:
ax 2 +c=0;
ax 2 +x=0;
ax 2 =0?
Как называются такие уравнения?
Какое квадратное уравнение называется приведенным?
Какие способы решения квадратных уравнений вы знаете?
От чего зависит наличие действительных корней квадратного уравнения?
Сколько корней может иметь квадратное уравнение?
Как вычислить дискриминант?
Какова формула корней квадратного уравнения?
Какова формула корней квадратного уравнения, в котором второй коэффициент является четным числом?
Сформулируйте теорему Виета.
Составьте квадратное уравнение по его корням x₁=–3; x₂= –10.
Составьте квадратное уравнение по его корням x₁= –7; x₂= –4.

Хорошо, разминка прошла успешно. Теперь выполним самостоятельную работу.

3. Самостоятельная работа.
Разложите квадратный трехчлен на множители, подобрав корни
по т. Виета.

а)х 2 – 8х + 15 = ( ) ( )
б)х 2 – 2х – 3 = ( ) ( )
в)х 2 – 4х + 4 = ( ) ( )

а)х 2 – 11х + 18 = ( ) ( )
б)х 2 – 7х + 12 = ( ) ( )
в)х 2 – 5х – 6 = ( ) ( )

(Проверяется на этом же уроке.)

4. Формирование новых понятий.
Сегодня мы рассмотрим на уроке частные случаи применения теоремы Виета, позволяющие устно найти корни полного квадратного уравнения ax 2 + bx + c = 0.
1) Рассмотрим уравнения х 2 + 2х – 3 = 0 и 2х 2 + 3х – 5 = 0.
Какова сумма коэффициентов в этих уравнениях? (1 + 2 – 3 = 0; 2 + 3 – 5 = 0) .
Определим корни этих уравнений. (х₁ = 1, х₂ = – 3 ) и (х₁ = 1, х₂ = – 2,5 ) .
Какое число является корнем каждого из них? Правильно, 1.

Приходим к выводу:
если в уравнении ax 2 + bx + c = 0 a+ b + c = 0 , то х₁ = 1, х₂ =. (*)
2) Рассмотрим уравнения х 2 – х – 2 = 0 и 2х 2 + 3х + 1 = 0.
Сравним сумму коэффициентов а и с в этих уравнениях с коэффициентом b.
(1 – 2 = – 1; 2 + 1 = 3) . Определим корни этих уравнений.
(х₁ =2, х₂= – 1) и (х₁= – 0,5, х₂= – 1).
Какое число является корнем каждого из них? Правильно, – 1.

Приходим к выводу:
если в уравнении ax 2 + bx + c = 0 a+ c = b , то х₁ = – 1, х₂ = – . (**)
Ребята, а как вы думаете, можно ли применять частные случаи теоремы Виета для приведенных квадратных уравнений? Найдите сумму и произведение корней.

Приведенные квадратные уравнения	X₁	X₂	X₁ + X₂	X₁ ∙ X₂
x 2 – 15x + 14 =0	1
x 2 + 8x + 7 = 0	— 1
х 2 + 9x + 20 = 0

Правильно, молодцы!
Используя теорему Виета можно вывести еще некоторые соотношения между корнями и коэффициентами приведенного квадратного уравнения.

1) Найдем сумму квадратов корней

Аналогично можно рассмотреть сумму кубов корней:

Таким образом, теорема Виета позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.
А теперь проверим, насколько вы усвоили сегодняшний материал и повторим изученное ранее.

5. Формирование умений и навыков.

5.1 Решите квадратное уравнение с помощью свойств (*) и (**).

а) х 2 + 5х – 6 = 0;
б) х 2 + 23х + 22 = 0;
в) 3х 2 – 4х + 1 = 0;
г) 5х 2 + 26х + 21 = 0;

д) х 2 + 6х – 7 = 0;
е) х 2 +17х + 16 = 0;
ж) 13х 2 – 18х + 5 = 0;
з) 7х 2 + 2х – 5 = 0.

5.2 Разложите на множители квадратный трехчлен, предварительно решив соответствующее квадратное уравнение:

а) х 2 – 6х + 5 ; б) – 2у 2 + 4у + 6 ; в) 30х 2 – 21х – 9 ; г) у 2 + 3у + 2 .

5.3 Числа х 1 и х 2 – корни квадратного уравнения х 2 – 7х – 1 = 0. Составьте квадратное уравнение, корнями которого являются числа 5х₁ и 5х₂.

5.4 Упростите выражение :

Данное уравнение действительно имеет два различных корня х₁ и х₂,т.к. D = 49 + 4 > 0. По теореме Виета х₁ + х₂ = 7, х₁х₂ = – 1 . Составим приведенное квадратное уравнение х 2 + рх + q = 0, имеющее корни 5х₁ и 5х₂:
р = – (5х₁ + 5х₂) = – 5(х₁+ х₂) = – 5·7 = – 35,q= 5х₁·5х₂= 25х₁·х₂ = 25· (– 1) = –25.
Следовательно, искомое уравнение: х 2 – 35х – 25 = 0.

6. Подведение итогов урока.

Школьники всего мира знают имя Франсуа Виета в связи с изучением данной теоремы. Это ли не честь ученому? Лучшего памятника трудно придумать!

А сейчас ребята продемонстрируют творческое задание презентацию с историческими сведениями о замечательном математике Ф. Виете.

7. Домашнее задание. П.4.6, № 339, 340.

Литература:

С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин . Алгебра 8 класс – М.: Просвещение, 2006 г
М.К. Потапов, А.В. Шевкин. Дидактические материалы для 8 класса – М.: Просвещение, 2006 г
В.Н. Студенецкая, Л.С. Сагателова. Сборник элективных курсов. Математика 8 – 9 . Волгоград. «Учитель», 2006 г