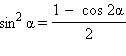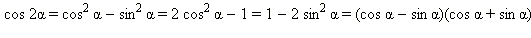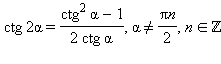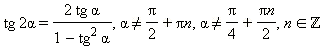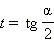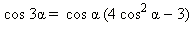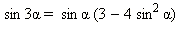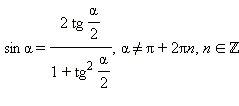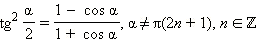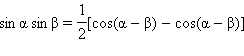Особые случаи при решении тригонометрических уравнений

Видео:Тригонометрические уравнения. Как запомнить частные случаи.Скачать

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

1. Корни уравненияcosx=a.

При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

1. Какие уравнения называют простейшими тригонометрическими?
2. Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
3. Выведите формулы решения простейших тригонометрических уравнений.
4. Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Видео:Тригонометрические уравнения (Частные случаи)Скачать

Особые случаи при решении тригонометрических уравнений

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Методы решения тригонометрических уравнений.

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

1. Алгебраический метод.

( метод замены переменной и подстановки ).

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно tan .

П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

корни этого уравнения: y ₁ = — 1, y ₂ = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

Видео:Решение тригонометрических уравнений. 10 класс.Скачать

4. Переход к половинному углу.

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

Видео:Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

5. Введение вспомогательного угла.

где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение прини мает вид:

Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

6. Преобразование произведения в сумму.

П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е . Преобразуем левую часть в сумму:

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Частные случаи тригонометрических уровнений

Дата добавления: 2015-08-14 ; просмотров: 2797 ; Нарушение авторских прав

Формулы сложения

cos (α + β) = cos α cos β – sin α sin β

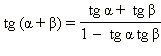
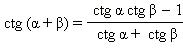
cos (α – β) = cos α cos β + sin α sin β

sin (α + β) = sin α cos β + cos α sin β

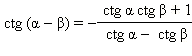
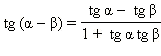
sin (α – β) = sin α cos β – cos α sin β

Формулы понижения степени

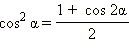
Формулы двойных и кратных углов

sin 2α = 2 sin α cos α

Универсальная замена

Формулы половинного аргумента

Преобразование произведения в сумму

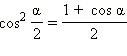
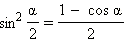
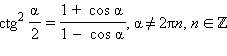
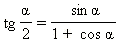
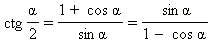
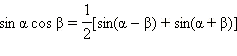
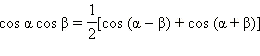
Частные случаи тригонометрических уровнений

· Уравнение sin x = a

x = ( —1) n arcsin a + πn, n ∈ Z.
Частные случаи:
1. sin x = 0 ⇒ x = πn, n ∈ Z.
2. sin x = 1 ⇒ x = π/2 + 2πn, n ∈ Z.
3. sin x = -1 ⇒ x = -π/2 + 2πn, n ∈ Z.

· Уравнение tg x = a

x = arctg a + πn, n ∈ Z.

x = ±arccos a + πn, n ∈ Z.

Частные случаи:
1. cos x = 0 ⇒ x = π/2 + πn, n ∈ Z.
2. cos x = 1 ⇒ x = 2πn, n ∈ Z.
3. cos x = -1 ⇒ x = π + 2πn, n ∈ Z.

💡 Видео

А ты знаешь, когда в тригонометрических уравнениях писать пk, а когда 2пk? #математика #егэ2023 #егэСкачать

Решение тригонометрических уравнений. 10 класс.Скачать

частные случаи тригонометрических уравненийСкачать

Алгебра 10 класс. Частные случаи решения тригонометрических уравненийСкачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Простейшие тригонометрические уравненияСкачать

Решение простейших тригонометрических уравнений. Частные случаиСкачать

Простейшие тригонометрические уравнения. y=cosx. 2 часть. 10 класс.Скачать

ТРИГОНОМЕТРИЯ ЗА 7 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Математика. Тригонометрия. Тема 118. Тригонометрические уравнения. Частные случаиСкачать