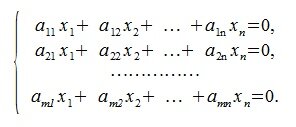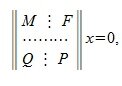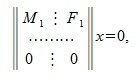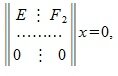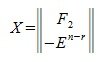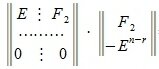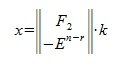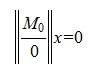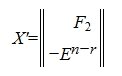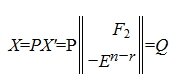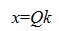Особенности однородных систем линейных уравнений

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Системы линейных однородных уравнений

Назначение сервиса . Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Видео:§41 Решение систем линейных однородных уравненийСкачать

Свойства систем линейных однородных уравнений

Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.

Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.

Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из ( n-r ) решений.

Видео:Видеоурок "Однородные системы линейных уравнений"Скачать

Однородная система линейных уравнений

Рассмотрим систему линейных уравнений (СЛУ):

Представим (1) в матричном виде:

где A m×n матрица, x вектор столбец порядка n , 0 — нулевой вектор столбец порядка m.

СЛУ (1) (или (2)) называется однородной системой линейных уравнений, т.к. правая часть системы равна нулю.

Однородная система линейных уравнений всегда совместна, т.к. вектор 0 всегда является решением системы (1):

Это решение называется нулевым или тривиальным решением.

1. Cистема линейных однородных уравнений имеет ли другие решения, кроме нулевого.
2. При каких условиях система линейных однородных уравнений имеет нетривиальное решение.
3. Как найти множество всех решений системы однородных линейных уравнений.

Если A n×n матрица и rank( A)= n, то нулевой вектор является единственным решением системы (1), в противном случае система имеет множество решений.

Видео:Решение системы уравнений методом ГауссаСкачать

Обшее решение однородной системы линейных уравнений

Пусть A m×n — матрица rank A=r. В общем случае можем предположить что r r столбцов матрицы A линейно независимы. Для удобства записи предположим, что это первые r столбцы матрицы A. Переставляя строки матрицы можно добиться того, чтобы подматрица матрицы A порядка r×r, расположенная в левом верхнем углу, была невырожденной. Запишем систему (2) в блочном виде:

где M — r×r — матрица, rang M=r.

Применяя метод исключения Гаусса для системы (3), получим:

где M₁ верхняя треугольная матрица, 0 — нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:

где E — единичная матрица порядка r×r.

где F₂— r×(n-r) — матрица, E n-r — единичная матрица порядка n-r, X — матрица порядка n×(n-r).

В уравнении (5) вместо x подставляя матрицу (6), получим:

Таким образом, векторы столбцы матрицы X являются решением системы (2) (или (1)). Более того, эти векторы линейно независимы и их линейная комбинация также является решением (2).

Общее решение системы однородных линейных уравнений имеет следующий вид:

гдe k — произвольный вектор столбец порядка n-r.

Общее решение системы однородных линейных уравнений можно также записать в следующем виде:

где x_i — i-ый вектор-столбец матрицы X, а k_i — i-ая координата вектора k

Множество всех решений (8)(или (9)) образует ядро или нуль пространство матрицы A и обозначается через Ker (A) или N(A).

В начале этого параграфа мы предполагали, что линейные независимые r векторы столбцы расположены в начале матрицы A. В общем случае, если они расположены в произвольных местах, аналогично вышеизложенному, применяя метод Гаусса, затем обратный ход Гауссова исключения и, наконец , разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует), получим

Сделаем замену переменных:

где P -матрица перестановок поядка n×n выбрана так, чтобы при подстановке (11) в (10) получили:

где E — единичная матрица порядка r×r.

Аналогично вышеизложенному векторы столбцы матрицы X’:

образуют множесво всех решений однородной системы линейных уравнений (12).

Учитывая (11) получим:

Общее решение системы однородных линейных уравнений имеет следующий вид:

гдe k — произвольный вектор столбец порядка n-r.

Общее решение системы однородных линейных уравнений можно также записать в следующем виде:

где q_i — i-ый вектор-столбец матрицы Q, а k_i — i-ая координата вектора k

Видео:Однородное уравнение в системеСкачать

Нахождение общего решения однородной системы линейных уравнений с помощью псевдообратной матрицы

Если rank(A)= r, r общее решение можно представить в следующем виде:

где E —единичная матрица, A + — псевдообратная к A матрица.

Для проверки подставим (16) в (2):

Ax=A(E−A + A)z=(A−AA + A)z=(A−A)z=0.

Ранг матрицы rank( E−A + A)= n-r. Следовательно столбцы матрицы E−A + A образуют множество всех решений системы (2).

Отметим, что r столбцов матрицы E−A + A линейно зависимы. Для исключения линейно зависимых столбцов можно сделать скелетное разложение. Тогда E−A + A= QS, где Q n×n−r — матрица rank (Q)=n−r, S n−r×n-матрица rank (S)=n−r. Тогда множество всех решений однородной системы линейных уравнений примет следующий вид:

Видео:Решение однородных линейных систем. ТемаСкачать

Решение однородной системы линейных уравнений онлайн

Для решения однородной системы линейных уравнений пользуйтесь онлайн калькулятором который решает однородную систему по шагам и находит полное решение.

Видео:9 класс, 12 урок, Однородные системы. Симметрические системыСкачать

Особенности решения системы линейных однородных уравнений

Однородным называется уравнение, у которого свободный член равен нулю.

Система линейных однородных уравнений всегда совместна, т.к. обладает нулевым решением.

Если в системе линейных однородных уравнений число независимых уравнений меньше числа неизвестных ( ), то она неопределенная, т.к. помимо нулевого решения обладает бесконечным множеством ненулевых решений.

Вопросы для самопроверки

¨ Что включает в себя множество, называемое векторным пространством, и какие операции в нем определены?

Какой размерности векторное пространство составляют решения совместной системы линейных уравнений с неизвестными?

Что представляет собой сумма векторов?

Что представляет собой произведение вектора на число?

Какой вектор называется линейной комбинацией других векторов?

Чем различаются линейно зависимые и линейно независимые системы векторов?

Выполнение какой зависимости свидетельствует о линейной зависимости векторов?

Что называется базисом векторного пространства?

Какая система единичных векторов служит базисом -мерного векторного пространства?

Сколько различных линейно независимых систем векторов существует в векторном пространстве?

Из скольких векторов состоит каждый базис -мерного векторного пространства?

Как называется максимальное число линейно независимых строк или столбцов матрицы?

Какое число называется минором -ого порядка матрицы ?

О какой зависимости между строками или столбцами квадратной матрицы свидетельствует равенство нулю ее определителя?

Если в определенной матрице минор некоторого порядка равен нулю, то чему равны миноры более высокого порядка в этой же матрице?

Как получается окаймляющий минор?

Что можно сказать о решении системы линейных уравнений с неизвестными, если ранг матрицы ее коэффициентов при неизвестных равен рангу соответствующей расширенной матрицы?

Что можно сказать о решении системы линейных уравнений с неизвестными, если ранг матрицы ее коэффициентов при неизвестных меньше ранга соответствующей расширенной матрицы?

Что можно сказать о решении системы линейных уравнений с неизвестными, если ранг матрицы ее коэффициентов при неизвестных равен рангу соответствующей расширенной матрицы и равен числу, меньшему числа неизвестных?

Что можно сказать о решении системы линейных уравнений с неизвестными, если ранг матрицы ее коэффициентов при неизвестных равен рангу соответствующей расширенной матрицы и равен числу неизвестных, не большему числа уравнений?

Сколько переменных системы линейных уравнений можно назвать базисными, а сколько – свободными, если ранг матрицы этой системы равен числу уравнений, меньшему числа неизвестных?

Чем определяется максимально возможное число групп базисных переменных?

Какие уравнения называются однородными?

В каком случае система линейных однородных уравнений является неопределенной?

💥 Видео

ФСР. Система однородных уравнений. Общее решениеСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Решение системы линейных однородных уравнений (№726)Скачать

Однородная система слау. Тривиальное решение. Ненулевое решениеСкачать

Фундаментальная система решений для однородной системы линейных уравненийСкачать

Однородные системы (02)Скачать

Решение однородных и неоднородных систем линейных уравнений. Нахождение ФСР.Скачать

Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Неоднородная система линейных уравненийСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

ФСР системы линейных уравнений. Алгоритм ГауссаСкачать