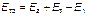Электрическое состояние цепей синусоидального тока, так же как и цепей постоянного тока, описывается с помощью уравнений, составленных в соответствии с законами Кирхгофа.
В общем виде тригонометрическое уравнение по первому закону Кирхгофа для узла цепи синусоидального тока имеет вид

где n – число ветвей, сходящихся в узле.
Этому уравнению соответствует уравнение первого закона Кирхгофа в комплексной форме (например, для действующих значений)

Правила знаков при составлении уравнений (58) остаются теми же, что и в цепях постоянного тока: токи, положительные направления которых направлены от узла, следует брать со знаком минус, а токи, положительные направления которых направлены к узлу – со знаком плюс.
Для любого контура цепи с синусоидальными напряжениями справедливо тригонометрическое уравнение, составленное по второму закону Кирхгофа.
В идеализированных электрических цепях магнитное поле считается сосредоточенным только на участках цепи, содержащих индуктивные элементы. При обходе замкнутого контура цепи всегда можно выбрать путь, лежащий вне переменного магнитного поля, а участок, содержащий индуктивный элемент, характеризовать разностью потенциалов, т. е. напряжением на его зажимах; при этом изменение потенциала в любом замкнутом контуре цепи синусоидального тока равно нулю. Поэтому, согласно второму закону Кирхгофа, алгебраическая сумма мгновенных значений напряжений всех участков замкнутого контура равна нулю:

где m — число участков, рассматриваемого контура.
Тригонометрическое уравнение можно заменить соответствующим ему комплексным уравнением второго закона Кирхгофа (например, для действующих значений)

Применительно к схемам замещения с источниками ЭДС второй закон Кирхгофа можно сформулировать таким образом: алгебраическая сумма комплексных напряжений на пассивных элементах замкнутого контура равна алгебраической сумме сторонних ЭДС, входящих в этот контур:

Правила знаков при составлении уравнений (60) и (61) остаются теми же, что и в цепях постоянного тока: слагаемые берут со знаком плюс в случае, когда направление обхода совпадает со стрелкой положительного направления соответственно напряжения, тока или ЭДС.
Последовательное соединение элементов в цепи синусоидального тока.
Рассмотрим в качестве примера цепь с последовательным включением резистора, индуктивной катушки и конденсатора. Такая цепь с достаточной точностью описывается схемой замещения, представленной на рисунке 13. Найдем связь между напряжением на входе цепи 
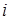
 |
Запишем уравнение по второму закону Кирхгофа в комплексной форме:

Выразим слагаемые правой части уравнения через комплексное значение тока 
и перепишем (62) в виде

Соотношение (63) является записью закона Ома рассматриваемой цепи в комплексной форме, а комплекс 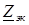

Таким образом, при последовательном соединении элементов цепи эквивалентное комплексное сопротивление цепи равно сумме комплексных сопротивлений всех последовательно включенных элементов, т. е. правило определения эквивалентного комплексного сопротивления последовательной цепи совпадает с аналогичным правилом для цепи постоянного тока. Очевидно, полученный результат справедлив для цепи с последовательным включением любого числа элементов.
Пример расчёта цепи синусоидального тока.
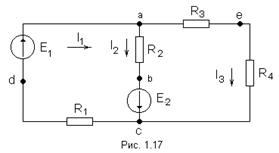
Произведём расчёт токов цепи синусоидального тока, представленной на рисунке 14.
 |

где 
Токи в схеме рисунка 14 можно рассчитать любым методом, аналогичным образом как для цепи постоянного тока.
Метод контурных токов.
В схеме рисунка 14 задаём направление неизвестных токов. Также выбираем направление контурных токов (например, по часовой стрелке). В схеме рисунка 14 можно выделить три контурных тока. Последовательные соединения 


 |
Для схемы рисунка 15 получаем эквивалентные сопротивления

источники ЭДС в комплексной форме
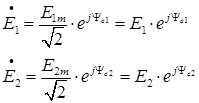
Для определения контурных токов необходимо составить следующую систему уравнений:

Уравнения для контурных токов можно записать в матричной форме:

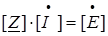
Решением уравнения (70) будет

Далее необходимо определить неизвестные токи через контурные токи:

Метод узловых потенциалов.
Аналогичным образом, как в методе контурных токов, представляем исходную схему в виде, представленном на рисунке 16.
 |
В схеме (рисунок 16) потенциал 

Уравнения для узловых потенциалов (73) можно записать в матричной форме:


где 


Решением уравнения (75) будет

Далее определяются токи

Баланс мощности.
Потребляемая полная мощность:

где 

Полная мощность источников:

где 

Потенциальная диаграмма.
Построим потенциальную диаграмму для левого контура, представленного на рисунке 17, исходной схемы (рисунок 14).
 |
На данном примере (рисунок 17) получаем

Если потенциалы (80) перенести на комплексную плоскость, то должна получиться замкнутая траектория. При этом, потенциал 
Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Основные законы и уравнения электрических цепей
Основными физическими законами, позволяющими описать любые режимы электрической цепи, являются законы Ома.
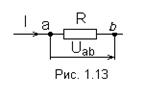
1. Закон Ома для участка цепи, не содержащего Э.Д.С., устанавливает связь между током и напряжением на этом участке (рис. 1.13)
 |
2. Закон Ома для участка цепи, содержащего источник Э.Д.С.
(обобщённый закон Ома)
Обобщённый закон Ома позволяет найти ток этого участка по известной разности потенциалов на концах участка цепи и имеющейся на этом участке Э.Д.С. E.
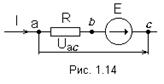
Имея в виду, что в неразветвлённом участке электрической схемы с произвольным числом Э.Д.С., сопротивлений и заданной разностью потенциалов на его концах, ток направлен от высшего потенциала к низшему.
Если предположить, что 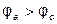
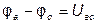
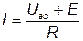
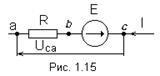
Если предположить, что 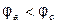
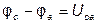
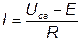
Основными уравнениями теории электрических цепей являются уравнения Кирхгофа, поэтому все электрические цепи подчиняются первому и второму законам Кирхгофа.
Оба эти закона установлены на основе многочисленных опытов и являются следствием закона сохранения энергии.
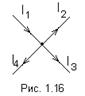 |
Первый закон Кирхгофа можно сформулировать двояко:
1. Алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю:

(Подтекающие к узлу токи считаются положительными, а утекающие – отрицательными).
2. Сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов:
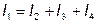
Второй закон Кирхгофа можно также сформулировать двояко:
1. Алгебраическая сумма напряжений (не падений напряжений) вдоль любого контура равна нулю
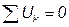
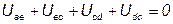
Алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме Э.Д.С. вдоль того же контура:
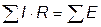
При составлении уравнений слагаемые берут со знаком плюс, если действующие на участках напряжения и Э.Д.С. совпадают с направлением обхода, и со знаком минус, если их действия противоположны направлению обхода.
При составлении уравнений для расчёта токов в схемах с помощью законов Кирхгофа необходимо придерживаться следующего алгоритма:
1. Произвольно задаются положительные направления токов.
2. Произвольно задаются положительные направления обхода контуров (с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми, например, по часовой стрелке).
3. Составляют уравнения по первому закону Кирхгофа. Число таких уравнений должно быть на единицу меньше числа узлов.
4. Недостающие уравнения составляют по второму закону Кирхгофа, при этом учитывают, чтобы в каждый новый контур входила, хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых записаны уравнения.
5. Решая полученную систему уравнений, находим неизвестные токи. Если какой — то ток или несколько токов, оказались отрицательными, то это значит, что действительное направление этих токов противоположно выбранному.
Дата добавления: 2016-02-02 ; просмотров: 656 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Основные законы и уравнения электрических цепей
Схема электрической цепи
Графическое изображение реальной электрической цепи с помощью условных символов и знаков называется электрической схемой.

При проведении расчетов каждый реальный элемент цепи заменяется элементами схемы.
В цепях постоянного тока чаще всего используют два основных элемента: источник энергии с Э.Д.С. Е c внутренним сопротивлением r0 и резистивный элемент (нагрузка) с сопротивлением R. Под внутренним сопротивлением генератора r0 понимают сопротивление электрическому току всех элементов внутри генератора.

Для проведения анализа электрической цепи важно выделить такие понятия, как ветвь, узел и контур.
Ветвь – участок электрической цепи, образованный последовательно соединёнными элементами и характеризующийся собственным значением тока в данный момент времени.
Узел – это точка соединения трёх и более ветвей (если на электрической схеме в месте пересечения двух линий стоит точка, то в этом месте есть электрическое соединение 2х линий, в противном случае его нет).
Контур – замкнутая часть цепи, состоящая из нескольких ветвей и узлов. Различают такие понятия, как геометрический и потенциальный узел.

Заземление любой точки схемы означает, что потенциал этой точки принят равным нулю. Токораспределение в такой схеме не изменяется, так как никаких новых ветвей, по которым могли бы протекать токи не образуется. Если же заземлить 2 точки схемы и более, то в этом случае в схеме токораспределение изменится.
Активные элементы
В линейных электрических цепях в качестве источников энергии различают источники Э.Д.С. и источники тока.
 |

Напряжение Uab зависит от тока приёмника и равно разности между Э.Д.С. генератора и падением напряжения на его внутреннем сопротивлении r0:

 |

По рис. 1.4 видно, что по мере нарастания тока в цепи напряжение на нагрузке возрастает, а, следовательно, уменьшается напряжение на выходных зажимах источника.
Источник тока характеризуется бесконечным внутренним сопротивлением и бесконечным значением Э.Д.С., при этом выполняется равенство:

L – параметр, который определяет способность катушки создавать магнитное поле. Он зависит от геометрических параметров катушки, числа её витков и от магнитных свойств сердечника, на который намотана катушка.
Из-за появления магнитного поля цепь будет пронизываться магнитным потоком. Для характеристики катушки индуктивности, как элемента электрической цепи достаточно вычислить потокосцеплениеψ. Индуктивность Lявляетсякоэффициентом пропорциональности между ψ и I:




Основные законы и уравнения электрических цепей
 |
Основными физическими законами, позволяющими описать любые режимы электрической цепи, являются законы Ома.
1. Закон Ома для участка цепи, не содержащего Э.Д.С., устанавливает связь между током и напряжением на этом участке (рис. 1.13)
2. Закон Ома для участка цепи, содержащего источник Э.Д.С.
Обобщённый закон Ома позволяет найти ток этого участка по известной разности потенциалов на концах участка цепи и имеющейся на этом участке Э.Д.С. E.
Имея в виду, что в неразветвлённом участке электрической схемы с произвольным числом Э.Д.С., сопротивлений и заданной разностью потенциалов на его концах, ток направлен от высшего потенциала к низшему.
 |
Если предположить, что 
Если предположить, что 


Основными уравнениями теории электрических цепей являются уравнения Кирхгофа, поэтому все электрические цепи подчиняются первому и второму законам Кирхгофа.
Второй закон Кирхгофа
Алгебраическая сумма напряжений (не падений напряжений) вдоль любого контура равна нулю
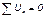
Алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме Э.Д.С. вдоль того же контура:
При составлении уравнений слагаемые берут со знаком плюс, если действующие на участках напряжения и Э.Д.С. совпадают с направлением обхода, и со знаком минус, если их действия противоположны направлению обхода.
При составлении уравнений для расчёта токов в схемах с помощью законов Кирхгофа необходимо придерживаться следующего алгоритма:
1) Произвольно задаются положительные направления токов.
2) Произвольно задаются положительные направления обхода контуров (с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми, например, по часовой стрелке).
3) Составляют уравнения по первому закону Кирхгофа. Число таких уравнений должно быть на единицу меньше числа узлов.
4) Недостающие уравнения составляют по второму закону Кирхгофа, при этом учитывают, чтобы в каждый новый контур входила, хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых записаны уравнения.
5)Решая полученную систему уравнений, находим неизвестные токи. Если какой — то ток или несколько токов, оказались отрицательными, то это значит, что действительное направление этих токов противоположно выбранному.
Первый закон Кирхгофа
Алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю:
(Подтекающие к узлу токи считаются положительными, а утекающие – отрицательными).
Сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов:
Метод контурных токов
Расчет методом контурных токов, так как он позволяет сократить число уравнений. При расчёте этим методом полагают, что в каждом независимом контуре схемы течёт свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей.
Если в схеме три контура, то систему уравнений для решения методом контурных токов записывают следующим образом:
В данной системе 



Сопротивления смежных ветвей 






Подставив все получившиеся значения в систему, вычисляем её главный определитель ∆, а также определители ∆1,∆2,∆3, полученные при подстановке на место 1-го, 2-го и 3-го столбцов соответственно значений столбца контурных Э.Д.С.
Находим значения контурных токов:
А также токи в ветвях, равные алгебраической сумме контурных токов:

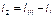


Для того, чтобы проверить правильность расчетов составляют баланс мощностей по формуле:
Если направление тока I, протекающего через Э.Д.С. E, совпадает с направлением Э.Д.С., то произведение EI входит в уравнение с положительным знаком, так как источник Э.Д.С. доставляет в цепь энергию.
🌟 Видео
Основы электротехники. 02. Электрическая цепьСкачать

Электрические цепи (часть 1)Скачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Урок 146 (осн). Изображение схем электрических цепейСкачать

Электрическая цепь и ее составные части. Сила тока. Напряжение. 8 класс.Скачать

Урок 144 (осн). Электрическая цепь и ее составные частиСкачать

Основные явления в электротехнической цепи и величины их характеризующаяСкачать

Урок 14. Законы Кирхгофа простыми словами с примерамиСкачать

Лекция 010-3. Основные законы электрических цепей - законы КирхгофаСкачать

Законы Кирхгофа. Метод контурных уравненийСкачать

Метод контурных токов - определение токов. ЭлектротехникаСкачать

Построение матриц электрических цепейСкачать

Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать
8 класс, 21 урок, Расчет электрических цепейСкачать

Введение в синусоидальное устойчивое состояние. Часть 1 (видео 42) | Анализ цепей | ЭлектротехникаСкачать

Урок 250. Задачи на расчет электрических цепей - 1Скачать

Лекция по электротехнике 1.3 - Пассивные элементы в электрической цепиСкачать

2020 г. Дифференциальные уравнения для электрических цепей. Лекция и практикаСкачать