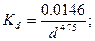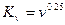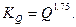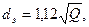Читайте также:
|
| Q, л/с | KQ | Q, л/с | KQ | Q, л/с | KQ | Q, л/с | KQ | Q, л/с | KQ | Q, л/с | KQ |
| 0,2 | 0,05982 | 5,2 | 17,91 | 10,5 | 61,25 | 299,3 | 973,4 | ||||
| 0,4 | 0,2011 | 5,4 | 19,13 | 66,43 | 319,8 | ||||||
| 0,6 | 0,4088 | 5,6 | 20,38 | 11,5 | 71,81 | 340,9 | |||||
| 0,8 | 0,6776 | 5,8 | 21,67 | 77,37 | 362,5 | ||||||
| 12,5 | 83,1 | 384,5 | |||||||||
| 1,2 | 1,376 | 6,2 | 24,36 | 88,98 | 407,3 | ||||||
| 1,4 | 1,802 | 6,4 | 25,75 | 13,5 | 95,06 | 430,4 | |||||
| 1,6 | 2,275 | 6,6 | 27,17 | 101,3 | 454,3 | ||||||
| 1,8 | 2,798 | 6,8 | 28,63 | 14,5 | 107,7 | 478,7 | |||||
| 3,363 | 30,12 | 114,2 | 503,7 | ||||||||
| 2,2 | 3,974 | 7,2 | 31,64 | 15,5 | |||||||
| 2,4 | 4,64 | 7,4 | 33,19 | ||||||||
| 2,6 | 5,324 | 7,6 | 34,78 | 16,5 | 581,6 | ||||||
| 2,8 | 6,062 | 7,8 | 36,41 | 142,3 | 608,7 | ||||||
| 6,837 | 38,05 | 17,5 | 149,7 | 636,3 | |||||||
| 3,2 | 7,654 | 8,2 | 39,73 | 157,3 | 664,3 | ||||||
| 3,4 | 8,513 | 8,4 | 41,45 | 18,5 | 692,8 | ||||||
| 3,6 | 9,408 | 8,6 | 43,19 | 172,9 | 722,1 | ||||||
| 3,8 | 10,34 | 8,8 | 44,97 | 19,5 | 180,9 | 751,8 | |||||
| 11,31 | 46,75 | 189,1 | 781,8 | ||||||||
| 4,2 | 12,32 | 9,2 | 48,59 | 205,9 | 812,6 | ||||||
| 4,4 | 13,37 | 9,4 | 50,45 | 223,4 | 843,7 | ||||||
| 4,6 | 14,45 | 9,6 | 52,36 | 241,5 | 875,2 | ||||||
| 4,8 | 15,56 | 9,8 | 54,27 | 261,3 | 907,4 | ||||||
| 16,72 | 56,23 | 279,4 | 940,1 |
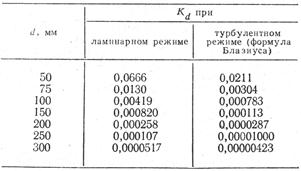
Если при движении жидкости в трубопроводе имеет место турбулентный режим в доквадратичной области шероховатых труб (практически весьма часто встречающийся случай), когда 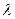
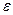
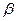
По-прежнему будем исходить из основной формулы Дарси— Вейсбаха (6.1); произведем в ней замену 
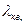

где 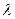
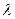
Учитывая далее выражение (6.9) и обозначая 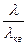
(поправочный коэффициент на «неквадратичность»), вместо формулы (6.14) будем иметь общее соотношение
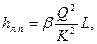
удобное для расчета трубопроводов в доквадратичной области турбулентного режима.
Для определения поправочного коэффициента на «неквадратичность» воспользуемся известными нам формулами для коэффициента гидравлического сопротивления (см. § 46), например формулой Альтшуля (4.53) — для доквадратичной области шероховатых труб и формулой Шифринсона (4.56) — для квадратичной области турбулентного режима.
При этом найдем

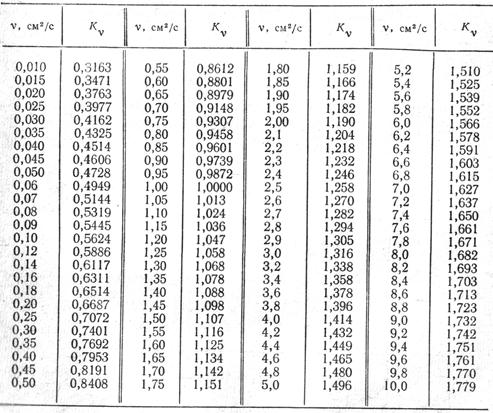
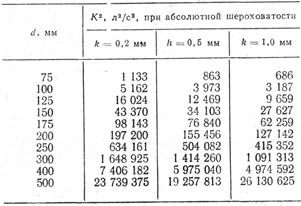
В табл. 48 приведены значения коэффициента 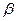
Значения этого коэффициента могут быть легко табулированы и для других случаев.
Таблица 48 Значения поправочного коэффициента 
§ 68. ОСНОВНЫЕ ЗАДАЧИ ПРИ РАСЧЕТЕ И ПРОЕКТИРОВАНИИ ТРУБОПРОВОДОВ
В первоначальной и наиболее общей постановке задачи при проектировании трубопроводов обычно задаются расход жидкости и положения начального и конечного пунктов трубопровода; в случае сложного трубопровода задача соответственно усложняется заданием ряда расходных пунктов и расходов на отдельных участках. В результате проведения топографических изысканий и сопоставления отдельных возможных вариантов на плане местности наносят трассу и строят продольный профиль трубопровода. Таким образом, при гидравлическом расчете оказываются известными также длина трубопровода и все его высотные отметки. Определению подлежат диаметр трубопровода и напор в его начальном сечении.
Рассматриваемая задача допускает множество решений, так как при прочих равных условиях диаметр одновременно определяет и потери напора: чем меньше диаметр, тем больше потери и, наоборот, чем больше диаметр, тем потери меньше. Поэтому при решении исходят из требований оптимальности и технической целесообразности сооружения и эксплуатации трубопровода.
Меньшие диаметры требуют значительно меньших капитальных затрат на сооружение трубопровода. Стоимость труб, объем земляных работ и работ по укладке труб тем меньше, чем меньше диаметр. Однако уменьшение диаметра трубопровода приводит к увеличению потерь напора, а следовательно, и к увеличению мощности насосов и двигателей, их стоимости и эксплуатационных расходов. Экономически наиболее выгодный диаметр должен соответствовать наименьшей полной стоимости трубопровода, зависящей от капитальных затрат на сооружение и прокладку самого трубопровода, расходов на сооружение насосных станций и эксплуатационных расходов.
По В. С. Яблонскому, приближенно можно принять, что экономически наивыгоднейший диаметр обычно соответствует скоростям течения жидкости примерно 1 м/с, т. е. диаметру, определяемому по формуле
где при расходе жидкости Q, выраженном в м 3 /с, диаметр dэ получается в м.
Для более точного определения экономически наивыгоднейшего диаметра существует ряд методов, изучаемых в специальных курсах по проектированию и сооружению трубопроводов. В основе этих методов лежит следующий прием. Составляют выражение для полной стоимости трубопровода, включая как капитальные затраты на его сооружение и прокладку, так и эксплуатационные расходы, выраженные в функции от диаметра трубопровода. Затем находят минимум этой функции, т. е. берут первую производную от стоимости по диаметру и приравнивают нулю; из получаемого таким образом уравнения определяют диаметр трубопровода, соответствующий минимуму его полной стоимости.
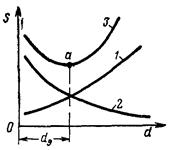
Искомое значение диаметра может быть определено также графическим способом; при этом по одной координатной оси (рис. 161), например оси абсцисс, откладывают диаметры трубопровода d, а по оси ординат — соответствующие этим диаметрам стоимости s — капитальные затраты (кривая 1) и эксплуатационные расходы (кривая 2). Далее суммированием ординат этих кривых находят полную стоимость трубопровода (кривая 3)., имеющую минимум в некоторой точке а, которая и определяет величину экономически наивыгоднейшего диаметра dэ.
Помимо основной задачи, рассмотренной выше в общей постановке, при гидравлическом расчете трубопроводов могут встретиться также следующие частные задачи:
Рис. 161. Рис. 162.
1) определение перепада напора, необходимого для пропуска заданного расхода жидкости по данному трубопроводу;
2) определение расхода жидкости по данному трубопроводу при заданном перепаде напора;
3) определение необходимого диаметра трубопровода для пропуска данного расхода при известном перепаде напора.
Затруднения при решении некоторых задач могут встретиться в случае, если число Рейнольдса невелико, т. е. коэффициент 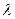
Решения указанных задач рассматриваются в следующих параграфах.
Дата добавления: 2015-04-18 ; просмотров: 172 ; Нарушение авторских прав
- Основные уравнения для расчета трубопроводов
- Самостоятельный гидравлический расчет трубопровода
- Постановка задачи
- Основные положения гидравлического расчета
- Подбор оптимального диаметра трубопровода
- Расчет падения напора и гидравлического сопротивления
- Расчет потерь давления
- Примеры задач гидравлического расчета трубопровода с решениями
- 📹 Видео
Видео:Видеолекция «Основы расчета и проектирования трубопроводов»Скачать

Основные уравнения для расчета трубопроводов
При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода на заданных расходе и потерях напора.
В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных передач.
Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы.
Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые исложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.
Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней жидкости, давлением газа.
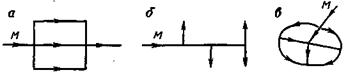
Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве (рис. 6.1), имеет общую длину l и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан). В начальном сечении трубопровода 1-1 геометрическая высота равна z1 и избыточное давление Р1, а в конечном сечении 2-2 — соответственно z2 и Р2. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна ν.
Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и α1 = α2, то скоростной напор можно не учитывать. При этом получим
Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором Нпотр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором Нрасп. Такой напор складывается из геометрической высоты Hпотр, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.
Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту
а последнее слагаемое Σh — как степенную функцию расхода
где K — величина, называемая сопротивлением трубопровода;
Q — расход жидкости;
m — показатель степени, который имеет разные значения в зависимости от режима течения.
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно
Численные значения эквивалентных длин lэкв для различных местных сопротивлений обычно находят опытным путем.
Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем
По этим формулам можно построить кривую потребного напора в зависимости от расхода. Чем больше расход Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор Нпотр. При ламинарном течении эта кривая изображается прямой линией (рис.6.2, а), при турбулентном — параболой с показателем степени равном двум (рис.6.2, б).
Крутизна кривых потребного напора зависит от сопротивления трубопровода K и возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.
Величина статического напора Нст положительна в том случае, когда жидкость движется вверх или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.
Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода.Характеристикой трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:
Простые трубопроводы могут соединяться между собой, при этом их соединение может бытьпоследовательным или параллельным.
Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рис. 6.3, а).
При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и Nравна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:
Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 6.3, б). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.
Параллельное соединение. Такое соединение показано на рис. 6.4, а. Трубопроводы 1, 2 и 3 расположены горизонтально.
Обозначим полные напоры в точках М и N соответственно HM и HN , расход в основной магистрали (т.е. до разветвления и после слияния) — через Q, а в параллельных трубопроводах через Q1, Q2 и Q3; суммарные потери в этих трубопроводах через Σ1 , Σ2 и Σ3.
Очевидно, что расход жидкости в основной магистрали
Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :
Отсюда делаем вывод, что
т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом
где K и m — определяются в зависимости от режима течения.
Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах ( Σ h). Пример такого построения дан на рис. 6.3, б.
Разветвленное соединение. Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб.
Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три трубы1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 6.5, а). Геометрические высоты z1, z2 и z3 конечных сечений и давления P1, P2 и P3 в них будут также различны.
Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме расходов в каждом трубопроводе:
Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода, получим (пренебрегая разностью скоростных высот)
Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как это делалось в п.6.1), получаем
Аналогично для двух других трубопроводов можно записать
Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1, Q2 и Q3 и HM.
Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) — сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3 , а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство HM > Hст1.
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).
Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б). магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE .
Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M — N и избыточные давления в конечных точках PB и PD и PE.
Для этого случая возможны два вида задач:
Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М.
Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви.
Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно:
уравнение равенства потребных напоров для ветвей CD и CE
уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD
выражение для потребного напора в точке М
Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом:
1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п.6.2).
Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.
Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рис. 6.7).
Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа). При этом основываются на двух обязательных условиях. Первое условие — баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки. Второе условие — баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой стрелки или против нее.
Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и длины семи участков. Требуется определить диаметры трубопроводов на всех участках.
Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода с насосом и принцип расчета трубопровода с насосной подачей жидкости.
Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость перекачивается из одной емкости в другую (рис. 6.8, а), или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рис. 6.8, б).
Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P 0 в другой резервуар с давлением P3 (рис. 6.8, а). Высота расположения оси насоса H1 называетсягеометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу,всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода H2 называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания.
Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1 (принимая α = 1):
Это уравнение является основным для расчета всасывающих трубопроводов.
Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений 2-2и 3-3:
Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса энергию жидкости можно будет аналогично выразить из уравнения:
Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается жидкости насосом и поэтому обозначается обычно Hнас.
Для нахождения напора Hнас вычислим уравнение :
где Δz — полная геометрическая высота подъема жидкости, Δz = H 1 + H2;
КQ m — сумма гидравлических потерь,
P3 и Р0 — давление в верхней и нижней емкости соответственно.
Если к действительной разности уровней Δz добавить разность пьезометрических высот ( P3 — Р0 ) ( ρg ), то можно рассматривать увеличенную разность уровней
и формулу можно переписать так:
Из этой формулы делаем вывод, что
Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.
На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в совместном построении в одном и том же масштабе и на одном графике двух кривых: напора Hпотр = f1(Q)и характеристики насоса Hнас = f2(Q) и в нахождении их точки пересечения (рис. 6.9).
Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рис. 6.9 дано два варианта графика: а — для турбулентного режима; б — для ламинарного режима. Точка пересечения кривой потребного напора с характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения вала насоса.
Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком.
Пусть в конце трубы, по которой движется жидкость со скоростью υ0, произведено мгновенное закрытие крана (рис. 6.10, а).
При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с увеличением давления на величину ΔPуд, которое называется ударным. Область (сечение n — n), в которой происходит увеличение давления, называется ударной волной. Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы — растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б).
Далее под действием перепада давления ΔPуд частицы жидкости устремятся из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-nперемещается обратно к крану с той же скоростью c, оставляя за собой выровненное давление P0 (рис. 6.10, в).
Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующему давлению P0. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость υ0, но направленную теперь в противоположную теперь сторону.
С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная ударная волна под давлением P0 — ΔPуд, которая направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака.
Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью υ0.
Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.
Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б.
Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.
Повышение давления при гидравлическом ударе можно определить по формуле
Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c определится по формуле:
где r — радиус трубопровода;
E — модуль упругости материала трубы;
δ — толщина стенки трубопровода;
K — объемный модуль упругости (см. п.1.3)
Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E = 
Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 — 1400 м/с.
При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период эксплуатации снижается (например, для водопроводных труб до 50% и даже ниже). Вследствие коррозии и образования отложений в трубах (инкрустации), шероховатость труб увеличивается. Это можно оценить по формуле:
где k0 — абсолютная шероховатость для новых труб, (мм),
kt — шероховатость через t лет эксплуатации,
α — коэффициент характеризующий быстроту возрастания шероховатости (мм/год).
Видео:гидравлический расчет трубопроводовСкачать

Самостоятельный гидравлический расчет трубопровода
Видео:Закон БернуллиСкачать

Постановка задачи
Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя. Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

- минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
- круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
- форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
- процесс изготовления труб круглой формы относительно простой и доступный.
Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.
Основными параметрами, характеризующими трубопровод являются:
- условный (номинальный) диаметр – DN;
- давление номинальное – PN;
- рабочее допустимое (избыточное) давление;
- материал трубопровода, линейное расширение, тепловое линейное расширение;
- физико-химические свойства рабочей среды;
- комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
- изоляционные материалы трубопровода.

Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.
Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода. Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.
Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.
Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.
Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.
Видео:Закон БернуллиСкачать

Основные положения гидравлического расчета
Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.
Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний, по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:
Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:
- ламинарный поток (Re 4000) – устойчивый режим, при котором в каждой отдельной точке потока происходит изменение его направления и скорости, что в итоге приводит к выравниванию скорости движения потока по объему трубы.
Критерий Рейнольдса зависит от напора, с которым насос перекачивает жидкость, вязкости носителя при рабочей температуре и геометрических размеров используемой трубы (d, длина). Данный критерий является параметром подобия для течения жидкости,поэтому, используя его, можно осуществлять моделирование реального технологического процесса в уменьшенном масштабе, что удобно при проведении испытаний и экспериментов.
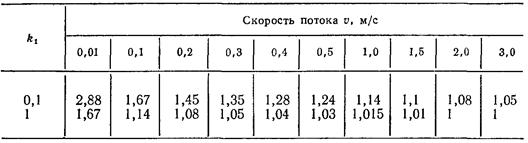
Проводя расчеты и вычисления по уравнениям, часть заданных неизвестных величин можно взять из специальных справочных источников. Профессор, доктор технических наук Ф. А. Шевелев разработал ряд таблиц для проведения точного расчета пропускной способности трубы. Таблицы включают значения параметров, характеризующих как сам трубопровод (размеры, материалы), так и их взаимосвязь с физико-химическими свойствами носителя. Кроме того, в литературе приводится таблица приближенных значений скоростей движения потока жидкости, пара,газа в трубе различного сечения.
Видео:Расчёт простого трубопроводаСкачать

Подбор оптимального диаметра трубопровода
Определение оптимального диаметра трубопровода – это сложная производственная задача, решение которой зависит от совокупности различных взаимосвязанных условий (технико-экономические, характеристики рабочей среды и материала трубопровода, технологические параметры и т.д.). Например, повышение скорости перекачиваемого потока приводит к уменьшению диаметра трубы, обеспечивающей заданный условиями процесса расход носителя, что влечет за собой снижение затрат на материалы, удешевлению монтажа и ремонта магистрали и т.д. С другой стороны, повышение скорости потока приводит к потере напора, что требует дополнительных энергетических и финансовых затрат на перекачку заданного объема носителя.
Значение оптимального диаметра трубопровода рассчитывается по преобразованному уравнению неразрывности потока с учетом заданного расхода носителя:
При гидравлическом расчете расход перекачиваемой жидкости чаще всего задан условиями задачи. Значение скорости потока перекачиваемого носителя определяется, исходя из свойств заданной среды и соответствующих справочных данных (см. таблицу).
Преобразованное уравнение неразрывности потока для расчета рабочего диаметра трубы имеет вид:
Видео:Расчёт сложных трубопроводовСкачать

Расчет падения напора и гидравлического сопротивления
Полные потери напора жидкости включают в себя потери на преодоление потоком всех препятствий: наличие насосов, дюкеров, вентилей, колен, отводов, перепадов уровня при течении потока по трубопроводу, расположенному под углом и т.д. Учитываются потери на местные сопротивления, обусловленные свойствами используемых материалов.
Другим важным фактором, влияющим на потери напора, является трение движущегося потока о стенки трубопровода, которое характеризуется коэффициентом гидравлического сопротивления.
Значение коэффициента гидравлического сопротивления λзависит от режима движения потока и шероховатости материала стенок трубопровода. Под шероховатостью понимают дефекты и неровности внутренней поверхности трубы. Она может быть абсолютной и относительной. Шероховатость различна по форме и неравномерна по площади поверхности трубы. Поэтому в расчетах используется понятие усредненной шероховатости с поправочным коэффициентом (k1). Данная характеристика для конкретного трубопровода зависит от материала, продолжительности его эксплуатации, наличия различных коррозионных дефектов и других причин. Рассмотренные выше величины являются справочными.
Количественная связь между коэффициентом трения, числом Рейнольдса и шероховатостью определяется диаграммой Муди.
Для вычисления коэффициента трения турбулентного движения потока также используется уравнение Коулбрука-Уайта, с использованием которого возможно наглядное построение графических зависимостей, по которым определяется коэффициент трения:
В расчётах используются и другие уравнения приблизительного расчета потерь напора на трение. Одним из наиболее удобных и часто используемых в этом случае считается формула Дарси-Вейсбаха. Потери напора на трение рассматриваются как функция скорости жидкости от сопротивления трубы движению жидкости, выражаемой через значение шероховатости поверхности стенок трубы:

Видео:Программные комплексы для моделирования. Расчет изотермического трубопровода Подбор оптимальногоСкачать

Расчет потерь давления
Рабочее давление в трубопроводе – это на большее избыточное давление, при котором обеспечивается заданный режим технологического процесса. Минимальное и максимальное значения давления, а также физико-химические свойства рабочей среды, являются определяющими параметрами при расчёте расстояния между насосами, перекачивающими носитель, и производственной мощности.
Расчет потерь на падение давления в трубопроводе осуществляют по уравнению:
Видео:Расчет всасывающих трубопроводовСкачать

Примеры задач гидравлического расчета трубопровода с решениями
Задача 1
В аппарат с давлением 2,2 бар по горизонтальному трубопроводу с эффективным диаметром 24 мм из открытого хранилища насосом перекачивается вода. Расстояние до аппарата составляет 32 м. Расход жидкости задан – 80 м 3 /час. Суммарный напор составляет 20 м. Принятый коэффициент трения равен 0,028.
Рассчитайте потери напора жидкости на местные сопротивления в данном трубопроводе.
Исходные данные:
Расход Q = 80 м 3 /час = 80·1/3600 = 0,022 м 3 /с;
эффективный диаметр d = 24 мм;
длина трубы l = 32 м;
коэффициент трения λ = 0,028;
давление в аппарате Р = 2,2 бар = 2,2·10 5 Па;
общий напор Н = 20 м.
Решение задачи:
Скорость потока движения воды в трубопроводе рассчитывается по видоизмененному уравнению:
w=(4·Q) / (π·d 2 ) = ((4·0,022) / (3,14·[0,024] 2 )) = 48,66 м/с
Потери напора жидкости в трубопроводе на трение определяются по уравнению:
HТ = (λ·l) / (d·[w 2 /(2·g)]) = (0,028·32) / (0,024·[48,66] 2 ) / (2·9,81) = 0,31 м
Общие потери напора носителя рассчитываются по уравнению и составляют:
Потери напора на местные сопротивления определяется как разность:
Ответ: потери напора воды на местные сопротивления составляют 7,45 м.
Задача 2
По горизонтальному трубопроводу центробежным насосом транспортируется вода. Поток в трубе движется со скоростью 2,0 м/с. Общий напор составляет 8 м.
Найти минимальную длину прямого трубопровода, в центре которого установлен один вентиль. Забор воды осуществляется из открытого хранилища. Из трубы вода самотеком изливается в другую емкость. Рабочий диаметр трубопровода равен 0,1 м. Относительная шероховатость принимается равной 4·10 -5 .
Исходные данные:
Скорость потока жидкости W = 2,0 м/с;
диаметр трубы d = 100 мм;
общий напор Н = 8 м;
относительная шероховатость 4·10 -5 .
Решение задачи:
Согласно справочным данным в трубе диаметром 0,1 м коэффициенты местных сопротивлений для вентиля и выхода из трубы составляют соответственно 4,1 и 1.
Значение скоростного напора определяется по соотношению:
w 2 /(2·g) = 2,0 2 /(2·9,81) = 0,204 м
Потери напора воды на местные сопротивления составят:
Суммарные потери напора носителя на сопротивление трению и местные сопротивления рассчитываются по уравнению общего напора для насоса (геометрическая высота Hг по условиям задачи равна 0):
Полученное значение потери напора носителя на трение составят:
Рассчитаем значение числа Рейнольдса для заданных условий течения потока (динамическая вязкость воды принимается равной 1·10 -3 Па·с, плотность воды – 1000 кг/м 3 ):
Re = (w·d·ρ)/μ = (2,0·0,1·1000)/(1·10 -3 ) = 200000
Согласно рассчитанному значению Re, причем 2320 0,25 = 0,316/200000 0,25 = 0,015
Преобразуем уравнение и найдем требуемую длину трубопровода из расчетной формулы потерь напора на трение:
l = (Hоб·d) / (λ·[w 2 /(2g)]) = (6,96·0,1) / (0,016·0,204) = 213,235 м
Ответ:требуемая длина трубопровода составит 213,235 м.
Задача 3
В производстве транспортируют воду при рабочей температуре 40°С с производственным расходом Q = 18 м 3 /час. Длина прямого трубопровода l = 26 м, материал — сталь. Абсолютная шероховатость (ε) принимается для стали по справочным источникам и составляет 50 мкм. Какой будет диаметр стальной трубы, если перепад давления на данном участке не превысит Δp = 0,01 мПа (ΔH = 1,2 м по воде)? Коэффициент трения принимается равным 0,026.
Исходные данные:
Расход Q = 18 м 3 /час = 0,005 м 3 /с;
длина трубопровода l=26 м;
для воды ρ = 1000 кг/м 3 , μ = 653,3·10 -6 Па·с (при Т = 40°С);
шероховатость стальной трубыε = 50 мкм;
коэффициент трения λ = 0,026;
Решение задачи:
Используя форму уравнения неразрывности W=Q/F и уравнение площади потока F=(π·d²)/4 преобразуем выражение Дарси – Вейсбаха:
∆H = λ·l/d·W²/(2·g) = λ·l/d·Q²/(2·g·F²) = λ·[(l·Q²)/(2·d·g·[(π·d²)/4]²)] = =(8·l·Q²)/(g·π²)·λ/d 5 = (8·26·0.005²)/(9,81·3,14²)· λ/d 5 = 5,376·10 -5 ·λ/d 5
d 5 = (5,376·10 -5 ·λ)/∆H = (5,376·10 -5 ·0,026)/1,2 = 1,16·10 -6
d = 5 √1,16·10 -6 = 0,065 м.
Ответ: оптимальный диаметр трубопровода составляет 0,065 м.
Задача 4
Проектируются два трубопровода для транспортировки невязкой жидкости с предполагаемой производительностью Q1 = 18 м 3 /час и Q2 = 34 м 3 /час. Трубы для обоих трубопроводов должны быть одного диаметра.
Определите эффективный диаметр труб d, подходящих под условия данной задачи.
Исходные данные:
Решение задачи:
Определим возможный интервал оптимальных диаметров для проектируемых трубопроводов, воспользовавшись преобразованным видом уравнения расхода:
Значения оптимальной скорости потока найдем из справочных табличных данных. Для невязкой жидкости скорости потока составят 1,5 – 3,0 м/с.
Для первого трубопровода с расходом Q1 = 18 м 3 /час возможные диаметры составят:
d1min = √(4·18)/(3600·3,14·1,5) = 0,065 м
d1max = √(4·18)/(3600·3,14·3.0) = 0,046 м
Для трубопровода с расходом 18 м 3 /час подходят трубы с диаметром поперечного сечения от 0,046 до 0,065 м.
Аналогично определим возможные значения оптимального диаметра для второго трубопровода с расходом Q2 = 34 м 3 /час:
d2min = √(4·34)/(3600·3,14·1,5) = 0,090 м
d2max = √(4·34)/(3600·3,14·3) = 0,063 м
Для трубопровода с расходом 34 м 3 /час возможные оптимальные диаметром могут быть от 0,063 до 0,090 м.
Пересечение двух диапазонов оптимальных диаметров находится в интервале от 0,063 м до 0,065 м.
Ответ: для двух трубопроводов подходят трубы диаметром 0,063–0,065 м.
Задача 5
В трубопроводе диаметром 0,15 м при температуре Т = 40°C движется поток воды производительностью 100 м 3 /час. Определите режим течения потока воды в трубе.
диаметр трубы d = 0,25 м;
расход Q = 100 м 3 /час;
μ = 653,3·10 -6 Па·с (по таблице при Т = 40°С);
ρ = 992,2 кг/м 3 (по таблице при Т = 40°С).
Решение задачи:
Режим течения потока носителя определяется по значению числа Рейнольдса (Re). Для расчета Re определим скорость движения потока жидкости в трубе (W), используя уравнение расхода:
W = Q·4/(π·d²) = [100/3600] · [4/(3,14·0,25²)] = 0,57 м/c
Значение числа Рейнольдса определим по формуле:
Re = (ρ·W·d)/μ = (992,2·0,57·0,25) / (653,3·10 -6 ) = 216422
Критическое значение критерия Reкр по справочным данным равно 4000. Полученное значение Re больше указанного критического, что говорит о турбулентном характере течения жидкости при заданных условиях.
Ответ: режим потока воды – турбулентный.
📹 Видео
Теоретические основы расчетов трубопроводов в ПК CPIPEСкачать

Как рассчитать диаметр трубопроводаСкачать

Урок гидравлики - 01 - Основные положенияСкачать

Общие принципы расчета элементов конструкцийСкачать

Расчет диаметра трубопроводов онлайнСкачать

Гидравлические сопротивления. Расчет оптимального диаметра трубопроводаСкачать

Расчет разветвленного трубопровода. Решение в MathCAD.Скачать

Лекция по Источникам Тепловой расчет трубопроводов 25 03 20Скачать

Уравнение Бернулли гидравликаСкачать

Расчет водоснабжения и отопления с уравнением БернуллиСкачать

4. Расчет параметров укладки трубопровода траншейным методомСкачать

Video 11 П2 Гидравлический расчет трубопроводаСкачать

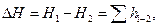

 (6.1)
(6.1)
 (6.2)
(6.2)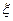 устанавливаются в зависимости от вида сопротивления на основании данных, приведенных в § 50.
устанавливаются в зависимости от вида сопротивления на основании данных, приведенных в § 50.
 (6.3)
(6.3)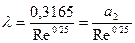 (6,4)
(6,4)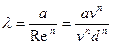 (6.5)
(6.5)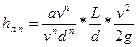 (6.6)
(6.6)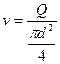
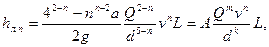 (6.7)
(6.7) k=5-n
k=5-n
 (6.8)
(6.8)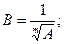
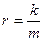
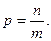

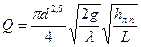
 (6.9)
(6.9)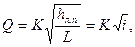
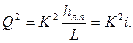 (6.10)
(6.10)
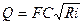
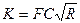 . (6.11)
. (6.11)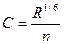 , а коэффициент шероховатости п = 0,0125
, а коэффициент шероховатости п = 0,0125
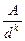 через Kd (коэффициент сечения), v п через Kv (вязкостный коэффициент), Q m через KQ (расходный коэффициент). Тогда получим следующую запись формулы для гидравлического уклона
через Kd (коэффициент сечения), v п через Kv (вязкостный коэффициент), Q m через KQ (расходный коэффициент). Тогда получим следующую запись формулы для гидравлического уклона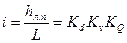 (6.12)
(6.12)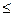 100 000)
100 000)