Тонкостенные сосуды и аппараты
Сосуды и аппараты, применяемые в газовой, нефтеперерабатывающей, химической, нефтехимической, пищевой, и смежных отраслях промышленности отличаются друг от друга конструктивным исполнением, материалом, размерами 
Тонкостенными принято считать сосуды и аппараты, если толщина их стенки S не превышает 10% внутреннего диаметра Dв. Такие сосуды и аппараты эксплуатируются обычно при давлении не более 10 МПа.
По ГОСТу 14249-89 тонкостенным называется сосуд, если:
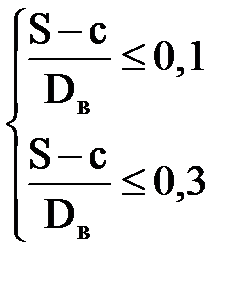 , , | для обечаек и труб при Dв ³ 200 мм | |||||||
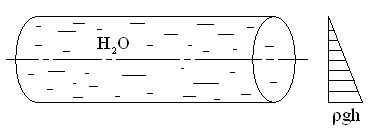
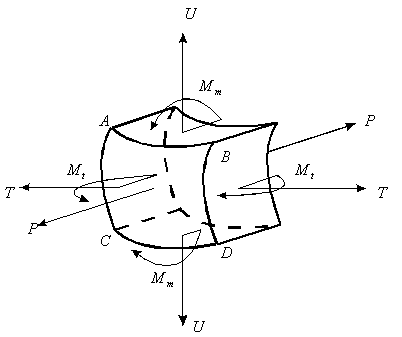
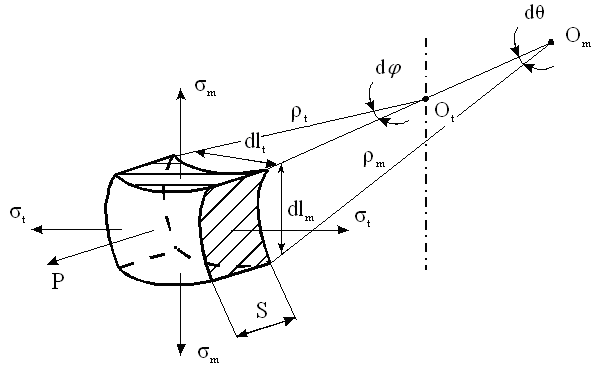
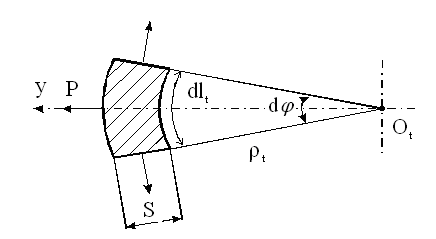
| для обечаек и труб при Dв Рисунок 3.1.3 – Эпюра распределения гидростатического давления для горизонтального аппарата внутренней поверхностей оболочки Меридианаминазываются кривые, образованные пересечением срединной поверхности плоскостями, проходящими через ось симметрии оболочки (рисунок 3.1.4). Рисунок 3.1.4 – Срединная поверхность Параллелями(параллельными кругами или кольцевыми сечениями) называются окружности, образованные пересечением срединной поверхности плоскостью, перпендикулярной оси оболочки. Полюсом оболочки называется точка пересечения срединной поверхности с осью (рисунок 3.1.5). Рисунок 3.1.5 – Основные параметры оболочки Параметры rm, rt называются радиусами кривизны соответственно меридиана и параллельного круга. Напряженное состояние материала упругих осесимметричных оболочек вращения При расчете оболочек вращения обычно определяют напряжения от действия внутреннего давления и толщину стенки. При этом рассматривают бесконечно малый элемент “D”, выделенный из оболочки двумя меридиональными и двумя кольцевыми сечениями (рисунок 3.1.6). Рисунок 3.1.6 – Элемент оболочки rm – радиус кривизны меридиана; rt – радиус кривизны параллельного круга. Как известно из курса сопротивление материалов, в самом общем случае от действия внешних нагрузок по каждой из граней могут действовать шесть внутренних силовых факторов (ВСФ): – продольное (нормальное) усилие (сила) Nz; – изгибающие Mx, My и крутящий Mz моменты, от которых возникают нормальные s (от Mx, My, Nz ) и касательные t (от Q x, Qy, Mz) напряжения. На рисунке 3.1.7 показаны внутренние силовые факторы только по одному из сечений – меридиональному, аналогично можно было бы изобразить внутренние силовые факторы и по остальным трем граням. Какие внутренние силовые факторы возникают в оболочке под действием внутреннего давления Рвнутр? Для решения этой задачи рассмотрим пример – воздушный шарик, находящийся под действием газового давления. Рисунок 3.1.7 – Внутренние силовые факторы, действующие на выделенный T, U– тангенциальные и меридиональные растягивающие усилия; Mt, Mm – тангенциальный и меридиональный изгибающий моменты; P – усилие от давления. Изобразим деформации стенки сферы (рисунке 3.1.8).
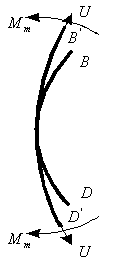
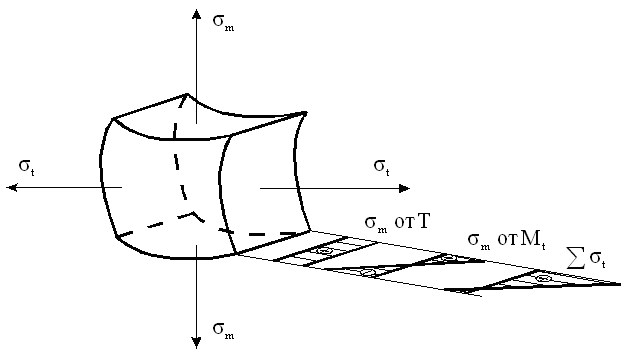
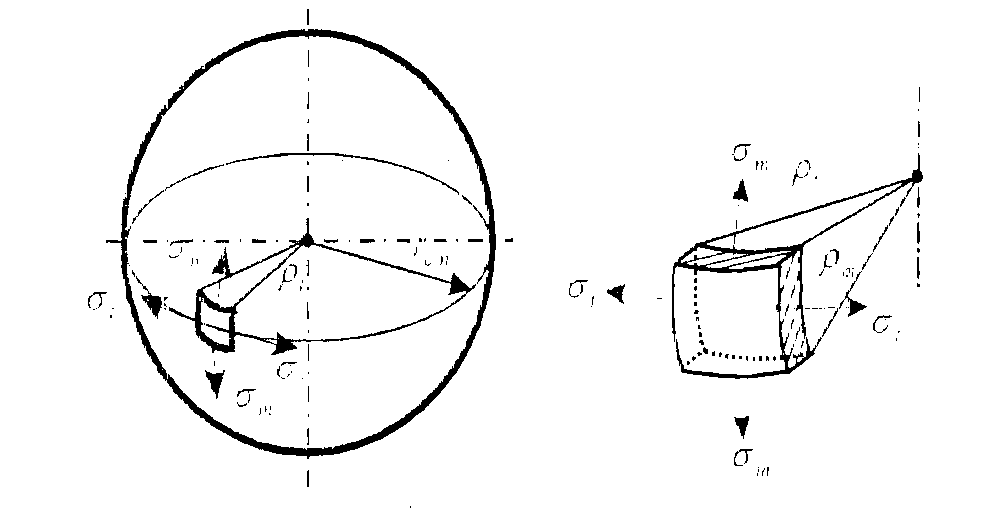
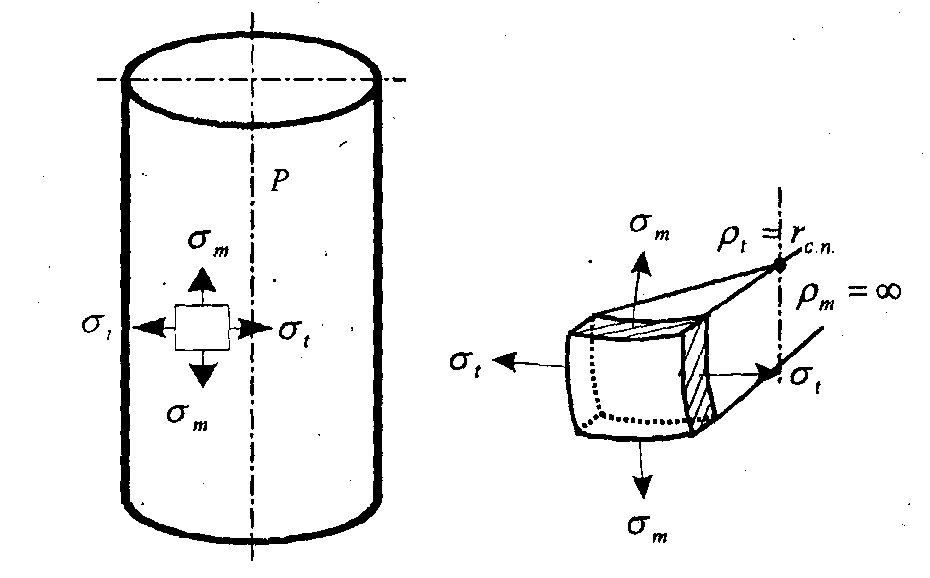
Рисунок 3.1.8 – Деформации сферической оболочки Допустим, надули шарик до давления P1 и он принял определенный размер, характеризующийся длиной окружности поперечного сечения. Надуваем шарик до давления P2 > Р1, размеры шарика увеличиваются и, соответственно, изменяются размеры дуги AB. Совместим эти дуги до деформации и после (рисунок 3.1.9). Рисунок 3.1.9 – Схема совмещения дуг AB и A’B’ Из рисунка видно, что дуги не совпадут, так как, во-первых, одна дуга длиннее другой, т.е. на нее должны действовать растягивающие усилия, в данном случае тангенциальные – T , а во-вторых, различна их кривизна. Изменить свою кривизну дуга может только под действием изгибающих моментов. Для рассматриваемого случая это – Мt. Если шарик повернуть на 90°, то параллельный круг превратится в меридиан. Для дуги BD будут происходить аналогичные изменения, т.е. на эту дугу будут действовать меридиональные растягивающие усилия U и меридиональный изгибающий момент Mm (рис.унок 3.1.10). Таким образом, в оболочках под действием внутреннего давления возникают усилия U и T и изгибающие моменты Мt, Мm. Рисунок 3.1.10 – Схема совмещения дуг BD и B’D’ Доказано, что в случае, когда вдоль меридиана не будет резких изменений внешней нагрузки, толщины оболочки и ее радиусов кривизны, то можно принять, что оболочка не подвергается изгибу, т.е. изгибающие моменты и поперечная сила равны нулю (Мx = Мy = Оy = 0), благодаря же симметрии формы и нагрузки оболочки действие крутящих моментов Мz и поперечной силы Оx на всех гранях исключено и тогда касательные напряжения отсутствуют. Таким образом, по граням действуют только нормальные усилия N; будем называть их соответственно меридиональными и обозначать N = U (по меридиональным сечениям АВ и СД) и тангенциальными (кольцевыми) N = Т (по граням АС и ВД). От них возникают нормальные напряжения, соответственно — меридиональные sm и тангенциальные st (рисунок 3.1.11). Рисунок 3.1.11 – Напряженное состояние и эпюры распределения тангенциальных напряжений по толщине стенки Кроме этого на грань АВСД действует внешняя нагрузка Р. (В данном примере это внутренне избыточное давление). От этой нагрузки возникает, так называемое, радиальное напряжение, направленное вдоль радиуса оболочки и равное по величине давлению, т. е. sr = Р. Так как для тонкостенных оболочек давление обычно меньше 10 МПа, то радиальное напряжение также не больше этого значения, и соответственно, значительно меньше допускаемых напряжений. Поэтому для тонкостенных оболочек обычно пренебрегают величиной радиальных напряжений и принимают их равными нулю. При расчете тонкостенных оболочек считают, что кольцевые и меридиональные напряжения постоянны по толщине оболочки, т.е. пренебрегают их изменением (рисунок 3.1.11), как это наблюдается для толстостенных аппаратов. Таким образом, можно принять, что напряженное состояние тонкостенных оболочек – плоское (двухосное). Основанная на этих предположениях теория, не учитывающая действие изгибающих моментов, а принимающая во внимание только продольные силы U и Т, называетсябезмоментной илимембранной теорией расчета оболочек, в отличие отмоментной теории. 3.1.3 Безмоментная теория расчета оболочек Определение напряжений Основным исходным уравнением безмоментной теории для расчета на прочность осесимметричных оболочек вращения, нагруженных внутренним избыточным давлением, является уравнение Лапласа. Для его нахождения рассмотрим равновесие выделенного элемента “Э” под действием равномерно распределенного внутреннего давления. Приложим внешние нагрузки и покажем внутренние силовые факторы, как изображено на рисунке 3.1.12. Рисунок 3.1.12 – Выделенный элемент оболочки, находящийся в равновесии под действием равномерно распределенного давления Рассмотрим условие равновесия всех сил на ось Y. Для наглядности рассмотрим этот элемент с двух видов (рисунок 3.1.12). Сумма всех сил, действующих вдоль оси Y, равна нулю, т.е. Рисунок 3.1.12 – Элемент оболочки. Вид сверху Как было сказано ранее на элемент действуют напряжение sm на гранях АС и ВD, а напряжение st на гранях АВ и СD. Кроме того, внешние силы, нормальная составляющая которых, относится к единице площади, есть Р (внутреннее давление). Составим уравнение равновесия в проекциях на нормаль (ось у), проведенную в середине элемента. На грани АВСD, площадь которой есть S*dlm, действует напряжение st. Таким образом, сила, действующая на указанной грани, равна Эта сила составляет с осью Y угол, равный Рассматривая совершенно аналогичные силы, действующие на грани АС и ВD, найдем, что проекция каждой из них на нормаль равна Наконец, составляющая внешней силы, направленная вдоль оси Y (по нормали), равна Находя сумму проекций на нормаль всех действующих на элемент сил и приравнивая эту сумму нулю, получим или, если вместо Т, U и P ’ подставить из (3.1.1) значения, выраженные через напряжения и внешнюю нагрузку, уравнение (3.1.4) примет вид В виду малости углов Сократив каждый член данного уравнения на Полученное уравнение носит название уравнение Лапласа. Одного этого уравнения недостаточно для определения напряжений sm и st, т.е. для нахождения этих напряжений к уравнению (3.1.8) нужно добавить еще одно уравнение. Для получения второго уравнения отсечем нормальным коническим сечением часть оболочки и отбросим верхнюю часть. Для оставшегося элемента (так называемой зоны оболочки), показанного на рисунке . составим уравнение равновесия всех сил в направлении оси оболочки Х. Площадь А поверхности поперечного сечения элемента есть кольцо. Поэтому На нее действует меридиональная сила U, от которой возникает напряжение Кроме этого, на выделенный элемент действует осевая равнодействующая Р’ внешних сил,приложенных к отсеченной части. В качестве внешних сил выступает равномерное внутреннее давление Р. Проектируя все силы на ось Х, получим где a – угол между направлением U и осью Х. Доказано, что если на какую-либо поверхность действует равномерно распределенное давление, то независимо от формы поверхности, проекция равнодействующей сил давления, на заданную ось равна произведению давления Р на площадь проекции поверхности А’ на плоскость, перпендикулярную к заданной оси. Следовательно Таким образом, для того чтобы определить проекцию равнодействующих сил давления на ось Х, нужно предварительно спроектировать поверхность на плоскость, перпендикулярную этой оси и определить ее площадь. Для рассматриваемой зоны проекция ее поверхности на плоскость, перпендикулярную оси Х, представляет собой окружность и площадь, соответственно, равна Подставляя значение Р’ в уравнение (3.1.13), получим Это уравнение называется уравнением равновесия зоны или просто уравнением зоны. Из этого уравнения находится меридиональное напряжение sm. Таким образом, по безмоментной теории напряжения sm и st в оболочке определяются из уравнений равновесия. Мембранная теория дает следующие значения напряжений для основных геометрических форм оболочек: – сферический сосуд (шаровая оболочка, полушаровое днище) (рисунок 3.1.13), нагруженный равномерно распределенным внутренним давлением Р. Для него rt = rm = R , где R – радиус сферы. Рисунок 3.1.13 – Сферическая оболочка, нагруженная внутренним давлением Тогда меридиональное напряжение sm равно кольцевому напряжению st и они определяются по формуле где rсп – радиус срединной поверхности, м. Рисунок 3.1.14 – Применение сферических оболочек для изготовления шаровых емкостей и полусферических днищ – цилиндр с крышками, нагруженный равномерно распределенным давлением Р. (рисунок 3.1.15) Рисунок 3.1.15 – Цилиндрическая обечайка то есть в продольных швах действуют в два раза большие напряжения, чем в поперечных (см. рисунок 3.1.11), и соответственно по этим швам в первую очередь может произойти разрыв при разрушении оболочки. – конус, шарнирно подвешенный по краю со стороны основания, нагруженный равномерно распределенным давлением Р. Кольцевые напряжения в любом сечении конического днища n — n можно найти из уравнения Лапласа. Учитывая, что величина где Из формул (3.1.24) и (3.1.25) вытекает, что максимальная величина кольцевых и меридиональных напряжений будет на краю конуса при r = R, причем при этом кольцевые напряжения (как и для цилиндра) в любом данном сечении в 2 раза больше меридиональных, т.е. У вершины конуса при г = 0 и кольцевые и меридиональные напряжения равны нулю. Пример эпюры тангенциальных напряжений приведен на рисунке 3.1.16. Риcунок 3.1.16 – Коническая оболочка, нагруженная внутренним давлением Те же значения будут справедливы и для усеченного конуса, закрытого днищем. Эти формулы верны в том случае, если угол a Содержание Видео:Сопротивление материалов. T-01 (безмоментная теория оболочек вращения, введение).Скачать  Безмоментная теория расчета тонкостенных оболочекБезмоментная теория расчета тонкостенных оболочек предполагает следующие допущения: — толщина оболочки должна быть достаточно малой по сравнению с ее другими геометрическими размерами. Например, для цилиндра толщина стенки должна составлять не более 10 % внутреннего диаметра; Вследствие малой толщины нормальные напряжения растяжения или сжатия по толщине оболочки не изменяются, величина их в R/s раз больше изгибных (R- радиус оболочки) что и определяет безмоментное состояние. — по форме сосуд обязательно должен представлять оболочку вращения; — нагрузка (давление на стенки) должна быть симметричной относительно оси вращения. Кроме этого, теория упрощается путем некоторой схематизации действительной работы конструкций. Эта схематизация формируется в используемыхгипотезах,аналогичных гипотезам в теории стержней, т.е.: — гипотезам плоских сечений; — гипотезам “не надавливания” слоев оболочки друг на друга. Следует отметить, что чем меньше отношение толщины (S) оболочки к ее радиусу R, тем точнее выполняется предположение о постоянстве напряжений по толщине и тем более точнее выполняются расчеты по безмоментной теории. Как было сказано ранее, в стенках оболочек при действии давления возникают напряжения: —σr — радиальные, действуют вдоль радиуса; — σt – тангенциальные, касательные к параллельному кругу; — σm –меридиональные, касательные к меридиану. При этом, на внутренних волокнах в точке 2 действуют все три напряженияσr, σtи σm (рисунок 1.21 а ), т.е. напряженное состояние — объемное, а на наружных в точке 1 – действуют только два напряжения σtи σm и напряженное состояние – плоское.Распределение напряжений по толщине стенки– неравномерное(рисунок 1.21 б). Рисунок 1.21– Элементы, вырезанные на наружной (1) и внутренней (2) поверхностях оболочки (ось х совпадает с меридианом) Радиальные напряжения на внутренних волокнах оболочки равны давлению Р (см рисунок 1.21). Но так как давление для тонких оболочек меньше 10 МПа, то радиальные напряжения значительно меньше допускаемых. Например, для стали Ст3 , допускаемое напряжение при 20 0 С равно 154 МПа. Поэтому для тонких оболочек пренебрегают радиальным напряжением, т.е. принимают σr = 0(рисунок 1.22) . В этом случае напряженное состояние материала тонких оболочек — плоскоеи для внутренних и наружных волокон(рисунок1.22).Также принимают, что напряжения σt и σm распределяются равномерно по толщине стенки, т.е. постоянны по S (рисунок 1.22). Рисунок 1.22 — Плоское напряженное состояние материала оболочки Рисунок 1.23 — Напряжения, действующие в стенках оболочек, распределены равномерно (показаны эпюры только тангенциальных напряжений) Кроме этого, как было сказано ранее, пренебрегают напряжениями, возникающими от изгибающих моментов. На рисунке 1.23 это σmот Мm . Остаются только напряжения σt и σm соответственно, от усилий (рисунок 1.24): — T Р –кольцевых (тангенциальных, окружных). При этом данные усилия и напряжения в любом поперечном сечении цилиндрической части корпуса колонны постоянны при действии равномерного газового давления. Рисунок 1.24 — Усилия и напряжения, возникающие в стенках тонких оболочках при расчете по безмоментной теории Для толстостенных оболочек (сосудов высокого давления — СВД) радиальные напряжения могут достигать значительных величин. Например, при внутреннем давлении, равном 300 МПа, радиальные напряжения на внутренних волокнах будут также равны 300 МПа, что значительно больше, чем допускаемое напряжение. Поэтому в этом случае нельзя пренебрегать радиальным напряжением и тогда напряженное состояние СВД – объемное. Таким образом, основная причина, по которой разделяю сосуды на тонкостенные и толстостенные – разные напряженные состояния: — для тонкостенных – плоское НС ( σr =0 ; σ m — для СВД – объемное НС σr Кроме того, для СВД учитывают, что напряжения распределяются по толщине стенки неравномерно. Резюмируя, можно сказать, что при расчете тонких оболочек по безмоментной теории при действии внутреннего давления принимают, что: — напряжения от изгибающих моментов малы и ими пренебрегают; — напряженное состояние плоское, т.е. не учитывают радиальные напряжения; — напряжения σt и σmпо толщине стенки распределяютсяравномерно. В этом случае, необходимо определить только меридиональные и кольцевые напряжения, причем только от усилий U и T. На участках удаленных от узла сопряжения (см. рисунок 1.20), указанные напряжения определяются по известным формулам безмоментной теории. Для цилиндрической оболочки данные зависимости имеют следующий вид где Сравнение формул показывает, что Из последнего выражения следует, что в продольных швах действуют в два раза большие напряжения, чем в поперечных (рисунок 1.25) и, соответственно, по этим швам или вдоль меридиана в первую очередь может произойти разрыв оболочки и ее разрушение (рисунок 1.26).
Рисунок 1.25 – Наиболее опасные продольные швы
Рисунок 1.26 – Разрушение происходит в продольном направлении (вдоль меридиана) Видео:КИР Расчет по безмоментной теорииСкачать  Безмоментная теория оболочекБезмоментная теория оболочек Когда можно считать, что вкладом изгибающих и крутящих моментов в НДС оболочки можно пренебречь по сравнению с вкладом усилий, в уравнениях равновесия соответствующие слагаемые можно опустить. В общем случае НДС оболочки можно разделить на две составляющих – мембранное и моментное. Первое характеризуется тем, что в напряжения основной вклад вносят усилия, а моменты пренебрежимо малы в силу, как правило, очень малой толщины оболочки. В этом случае цилиндрическая жесткость настолько мала, что даже при изгибаниях моментами модно пренебречь. Кроме того, такой вид НДС реализуется в так называемых мягких оболочках, когда материал не сопротивляется изгибу и работает только на растяжение – например, ткань парашюта, надувная емкость из ткани и т.п. Моментное НДС характеризуется тем, что решающий вклад в напряжения вносят именно моменты. Наиболее выраженным моментным состоянием является краевой эффект. Краевой эффект – быстро меняющееся и затухающее по мере удаления от линии искажения НДС. Линии искажения – общее название для случаев: — подкрепляющее ребро или ослабляющий надрез; Видео:Сопротивление материалов. Лекция: тонкостенные оболочки вращения (исправленное видео)Скачать  Рекомендуемые материалы— линия, где скачком меняется толщина; — линия, где скачком меняется нагрузка; — линия, где скачком меняется кривизна; — линия, где скачком меняются две или более из указанных величин. По этой причине НДС оболочки часто получают как сумму двух состояний – безмоментного НДС и краевого эффекта. Возникает вопрос, как оценить вклад усилий и моментов в суммарное НДС. Просто сравнивать усилия и моменты нельзя хотя бы по той причине, что это параметры с разной размерностью. Сравнение можно делать лишь путем сопоставления вклада усилий и моментов в напряжения. В простейшем случае на основе гипотезы прямых нормалей можно считать, что тогда можно считать, что и напряжения меняются по некоторому линейному закону Если с учетом этого получить выражения усилий и моментов, то Суммарные напряжения выражаются следующим образом Имея ввиду, что второе слагаемое в этих напряжениях – от момента – имеет максимальные значения при При равенстве моментов нулю исчезают и перерезывающие силы. Оставшиеся три уравнения равновесия приводятся к виду В этих трех уравнениях равновесия только три неизвестных величины – усилия После определения значений усилий можно получить деформации. Строго говоря, эти деформации должны удовлетворять условиям совместности. Если подчинить деформации этим условиям, сложность решения резко возрастает. Поэтому на практике принимается, что эти условия можно не учитывать. Анализ показывает, что возможная погрешность будет тем больше, чем сильнее нарушены условия безмоментности. После определения деформаций из геометрических соотношений отыскиваются перемещения. Для этого необходимо решить систему дифференциальных уравнений Решение этой системы неоднородных дифференциальных уравнений необходимо искать в виде суммы общего решения соответствующей однородной системы и частного решения исходной системы: Общее решение, отвечающее нулевым правым частям этой системы, большого интереса не представляет, т.к. в этом случае все деформации нулевые, а получаемые перемещения отвечают движению оболочки как твердого тела, без деформирования. Для отыскания частного решения необходимо сформулировать граничные условия – как и при любом интегрировании, нужны условия для определения постоянных интегрирования. Система уравнений равновесия имеет второй порядок по каждому из направлений, поэтому для определения постоянных интегрирования в каждой точке контура нужно поставить по одному условию в усилиях. После определения деформаций (по алгебраическим соотношениям – здесь граничные условия не требуются) определение перемещений требует постановки условий для перемещений в каждой точке контура – по одному условию. Необходимо иметь в виду, что для безмоментных оболочек нельзя ставить граничные условия, запрещающие прогибы, когда речь идет о граничных условиях в перемещениях – если запретить прогибы, в окрестности границы будут возникать моменты. По тем же соображениям нельзя ставить граничные условия в силовых параметрах Условия применимости безмоментной теории оболочек 1. Форма оболочки характеризуется плавностью срединной поверхности, отсутствием ребер и скачкообразных изменений толщины. 2. Закрепление оболочки на контуре не должно ограничивать прогибы и их производные. В направлении срединной поверхности закрепление должно исключать смещение оболочки как жесткого целого. 3. Нагрузка должна в области приложения меняться плавно, без скачков, и не должна включать в себя изгибающие или крутящие моменты и перерезывающие силы. В целом эти требования означают, что в оболочке не должно быть линий искажения. В окрестности каждой из линий искажения будет возникать т.н. краевой эффект, и лишь на некотором удалении от линии искажения можно считать НДС безмоментным. При наличии линий искажения безмоментная теория применима при условиях: 1. Линии искажения не образуют густую сетку, т.е. краевые эффекты от соседних линий не должны накладываться друг на друга. 2. Линии искажения не должны касаться т.н. асимптотических линий, т.е. таких, кривизна которых равна нулю (например, для цилиндра и конуса это прямые вдоль образующих). Этапы расчета оболочки по безмоментной теории 1. Определяются усилия из уравнений равновесия. 2. Определяются деформации из физических соотношений. 3. Определяются перемещения. Формально на этом можно поставить точку. Однако остается открытым вопрос о точности полученного решения. Поэтому есть рекомендации (А.Л. Гольденвейзер) для контроля точности выполнить еще три этапа: 1. Определить искривления через деформации. 2. Рассчитать моменты через искривления. 3. Определить перерезывающие силы. 4. Сопоставить вклад напряжений от моментов и усилий в общее НДС. Расчет цилиндрической оболочки при осевом сжатии, осесимметричный случай. Пусть цилиндрическая оболочка длиной l, радиусом R и толщиной h подвержена действию осевой сжимающей силы Р, равномерно распределенной по торцу x = 0. Торец оболочки x = l опирается на неподвижную плоскость. Принимаем систему координат в срединной поверхности – вдоль направляющей ось x и вдоль окружности ось y. В силу осевой симметрии второе из уравнений равновесия исчезает, а из первого уравнения, которое принимает вид следует N1 = const = C. Постоянная С определяется из условия на границе: Из последнего уравнения равновесия в силу равенств R1 = ∞, R2 = R следует N2 = 0. Таким образом, все усилия определились: После этого деформации определяются из физических соотношений: Перемещения отыскиваются из геометрических соотношений Последнее равенство следует из осевой симметрии. Постоянная интегрирования С определяется из условия нулевого смещения на опертом торце: при x = l необходимо u = 0, тогда Окончательно все перемещения На этом заканчивается решение – по схеме это первые три этапа. Следующие, поверочные этапы, в этой задаче можно не выполнять по той причине, что полученные перемещения либо постоянны (u и w), либо представляют собой линейные функции (u) координат. Поскольку искривления определяются как вторые производные от перемещений, то в нашем случае они автоматически будут нулевыми. Тогда и моменты равны нулю, и вклад их в НДС будет нулевым. Это пример расчета безмоментной оболочки с нулевыми погрешностями в рамках сделанной постановки. Расчет цилиндрической оболочки при постоянном внутреннем давлении, осесимметричный случай. Геометрия оболочки описывается теми же параметрами, что и в предыдущем примере. Составляющие внешней нагрузки будут Из соображений симметрии следует N12 = 0, и второе из уравнений равновесия выполняется тождественно. Первое и третье принимают вид Отсюда определяются все усилия: Постоянная С определяется из граничных условий. Например, при свободных торцах С = 0, в других случаях эта постоянная определяется из конкретных условий. Пока используем эту величину в общем виде. Деформации определяются из физических соотношений: Если оболочка зажата между двумя жесткими основаниями, то необходимо е1 = 0, и тогда С = νPR = νN2. Если днища оболочки не закреплены в осевом направлении, а подвержены внутреннему давлению, как и боковые стенки, то суммарное давление внутреннее уравновешивается осевыми усилиями: В этом случае постоянная определяется как С = PR/2. Для конкретности примем последний вариант. Тогда усилия и деформации будут Если использовать граничное условие u = 0 при x = 0, то перемещения определяются выражениями Формально решение получено точное, но практически реализовать такую форму деформирования «бочки», когда по всей ее длине прогибы постоянны, невозможно. Три обязательных этапа выполнены, оставшиеся вновь необязательны. Сферическая оболочка при внутреннем давлении, случай точечной (сферической) симметрии. Геометрия оболочки задается ее радиусом R и толщиной h. Из третьего уравнения равновесия, которое принимает вид 💡 ВидеоСопротивление материалов. T-03 (безмоментная коническая оболочка, внутреннее давление).Скачать  08 05 Сопротивление материалов РК5 43БСкачать  КиР Моментная teoreticalСкачать  Сопротивление материалов Лекция 31 осесимметричные оболочки, безмоментная теорияСкачать  Сопротивление материалов. Лекция 31 (осесимметричные оболочки, безмоментная теория).Скачать  Сопротивление материалов. T-02 (безмоментная цилиндрическая оболочка, внутреннее давление).Скачать  Сопротивление материалов. T-04 (безмоментная сферическая оболочка, внутреннее давление).Скачать  СС 1 1 Уравнения равновесия для безмоментных оболочекСкачать  Лекция 6. Семестр 2. Сопротивление материалов.Скачать  Сопротивление материалов. Лекция 32 (безмоментные оболочки, примеры расчёта)Скачать  Основные положения молекулярно-кинетической теории | Физика 10 класс #24 | ИнфоурокСкачать  Семинар 10 \ оболочкиСкачать  Основные положения молекулярно-кинетической теории газов и ее опытное обоснование. 10 класс.Скачать  Механика конструкций. Тема 5. Теория и практика расчета пластинСкачать  Сопротивление материалов. T-05 (безмоментная комбинированная оболочка, внутреннее давление).Скачать  |



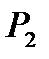





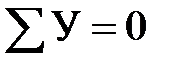
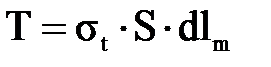 . (3.1.1)
. (3.1.1)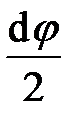 , и направлена в противоположную оси Y сторону, поэтому ее проекция на нормаль равна —
, и направлена в противоположную оси Y сторону, поэтому ее проекция на нормаль равна — 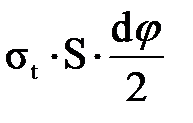 .
. (3.1.2)
(3.1.2)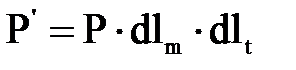 . (3.1.3)
. (3.1.3) , (3.1.4)
, (3.1.4)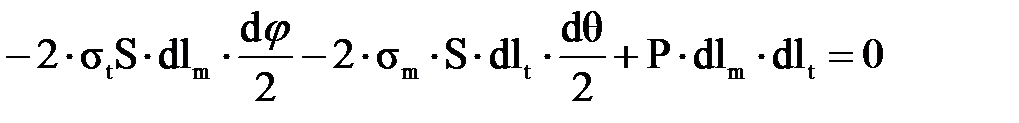 (3.1.5)
(3.1.5)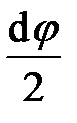 и
и 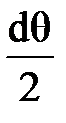 можно записать, что
можно записать, что 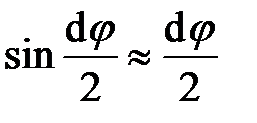 ,
, 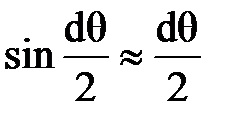 . Кроме того, используя зависимость между длной дуги и радиусом кривизны, получим
. Кроме того, используя зависимость между длной дуги и радиусом кривизны, получим 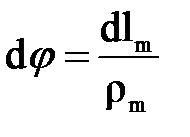 и
и 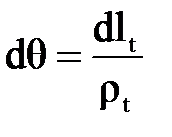 . Подставляя эти значения в уравнение (3.5), имеем
. Подставляя эти значения в уравнение (3.5), имеем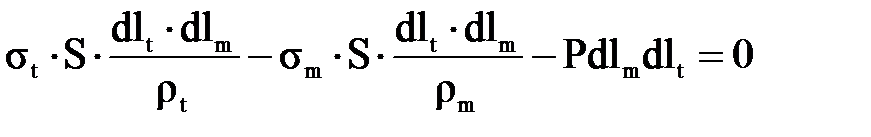 (3.1.6)
(3.1.6)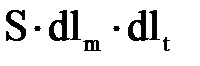 , его можно записать следующим образом
, его можно записать следующим образом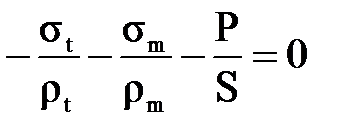 , (3.1.7)
, (3.1.7)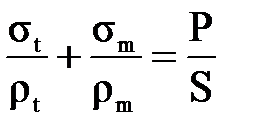 . (3.1.8)
. (3.1.8)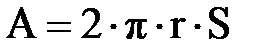 . (3.1.9)
. (3.1.9)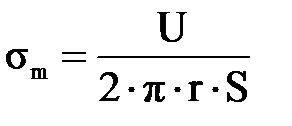 . (3.1.10)
. (3.1.10)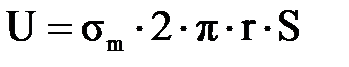 . (3.1.11)
. (3.1.11)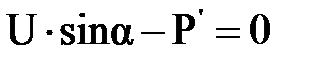 , (3.1.12)
, (3.1.12)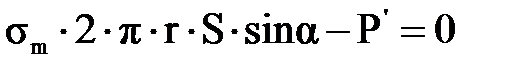 , (3.1.13)
, (3.1.13) . (3.1.14)
. (3.1.14) . (3.1.15)
. (3.1.15)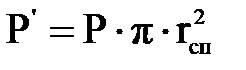 . (3.1.16)
. (3.1.16) (3.1.17)
(3.1.17) . (3.1.18)
. (3.1.18)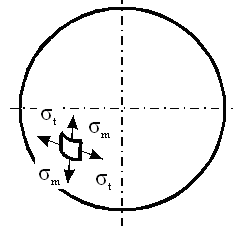
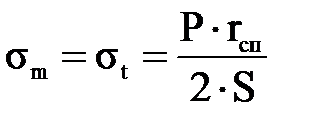 , (3.1.19)
, (3.1.19)
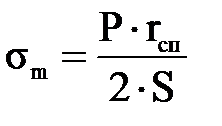 , (3.1.20)
, (3.1.20)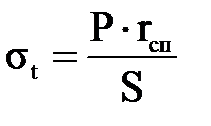 , (3.1.21)
, (3.1.21)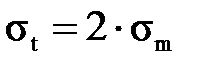 , (3.1.22)
, (3.1.22) , (3.23)
, (3.23)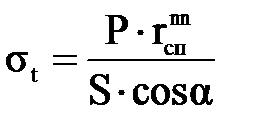 , (3.24)
, (3.24) ,
, 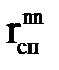 – соответственно радиус кривизны и радиус конуса в сечении n – n. Величину меридиональных напряжений, возникающих в сечении n – n конуса можно определить из уравнения зоны (4), т.е
– соответственно радиус кривизны и радиус конуса в сечении n – n. Величину меридиональных напряжений, возникающих в сечении n – n конуса можно определить из уравнения зоны (4), т.е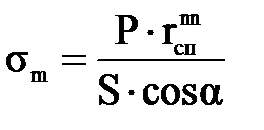 . (3.25)
. (3.25)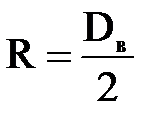 , (3.26)
, (3.26)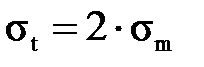 . (3.27)
. (3.27)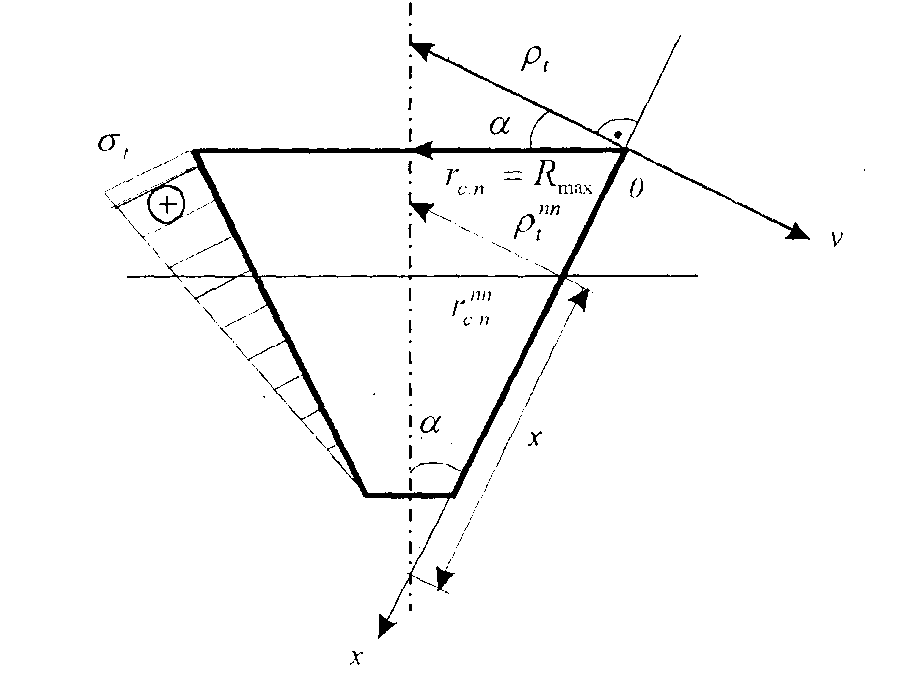



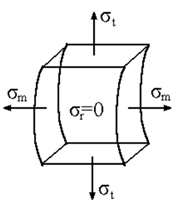


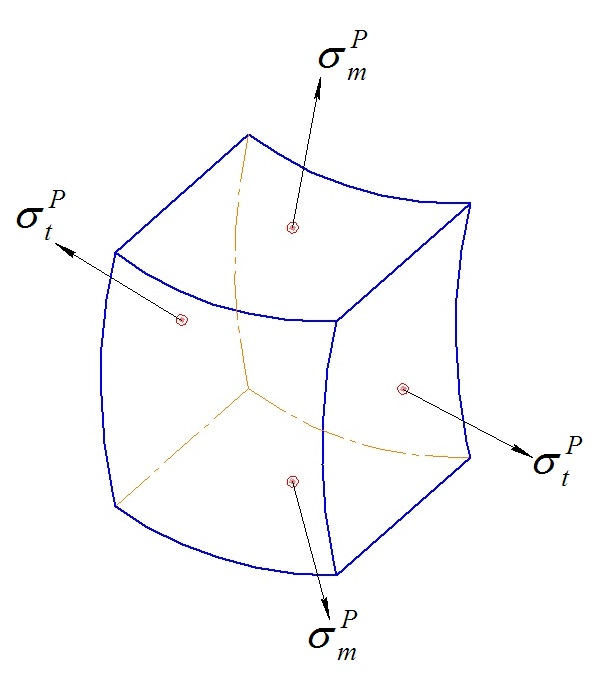
 0; σ т
0; σ т  0 ; σ m
0 ; σ m 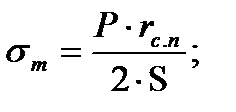 (1.14 )
(1.14 )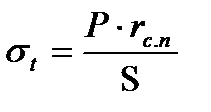 ( 1.15 )
( 1.15 ) — радиус срединной поверхности, мм.
— радиус срединной поверхности, мм.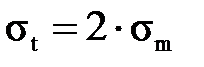 . (1.16)
. (1.16)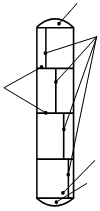







 оценивать вклад в напряжения от усилий и моментов нужно сопоставлением величин
оценивать вклад в напряжения от усилий и моментов нужно сопоставлением величин  и
и 


 Поэтому формально система замкнута и ее можно решать и определять усилия.
Поэтому формально система замкнута и ее можно решать и определять усилия.
















 получаются ненулевые усилия, и в итоге
получаются ненулевые усилия, и в итоге