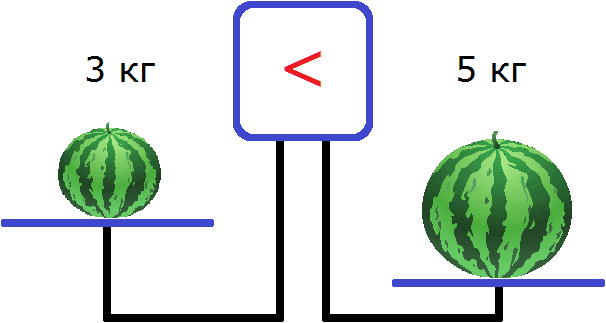
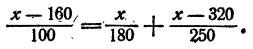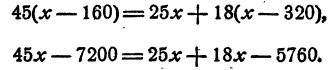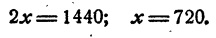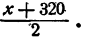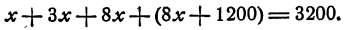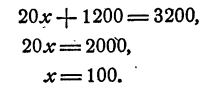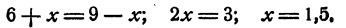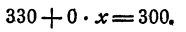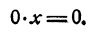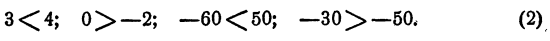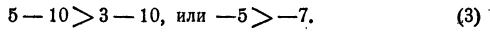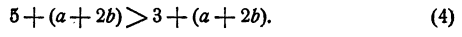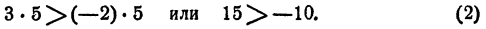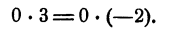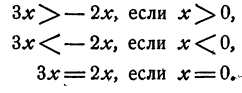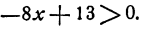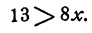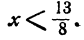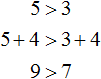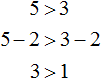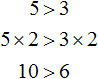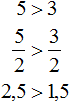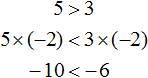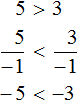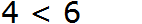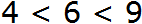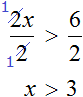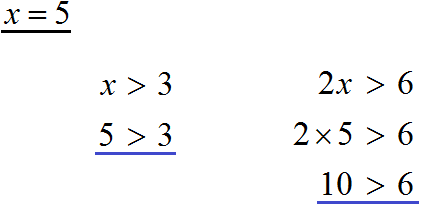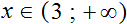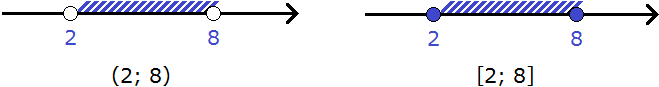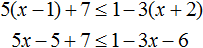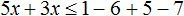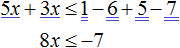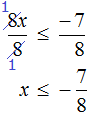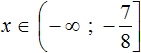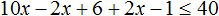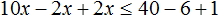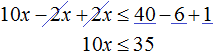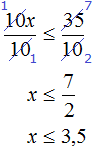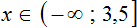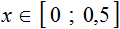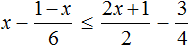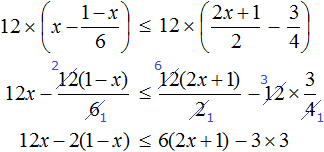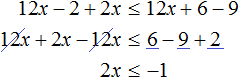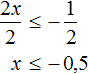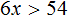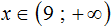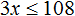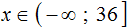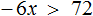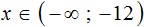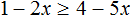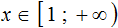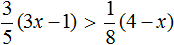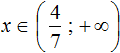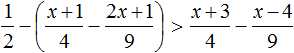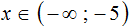С неравенствами мы познакомились в школе, где применяем числовые неравенства. В данной статье рассмотрим свойства числовых неравенств, не которых строятся принципы работы с ними.
Свойства неравенств аналогичны свойствам числовых неравенств. Будут рассмотрены свойства, его обоснования, приведем примеры.
- Числовые неравенства: определение, примеры
- Свойства числовых неравенств
- Основные свойства
- Другие важные свойства числовых неравенств
- Свойства числовых неравенств
- Уравнения и неравенства в математике с примерами решения и образцами выполнения
- Выражение
- Уравнение
- Равносильность
- Неравенство
- Параметр
- Примеры решения уравнений
- Приближенные методы вычисления корней
- Неравенства с одним неизвестным
- Примеры решения неравенств
- Способ подстановки
- Симметричные системы
- Линейные системы
- Тождества
- Доказательство неравенств
- Алгебраические уравнения
- Уравнения, тождества, неравенства: определения и классификация
- Уравнения и неравенства первой степени с одним неизвестным
- Два свойства уравнений
- Понятие о равносильности уравнений
- О некоторых преобразованиях уравнения, которые могут привести к потере или приобретению решений
- О числе решений уравнения первой степени с одним неизвестным
- Уравнения, содержащие неизвестное в знаменателе
- Решение задач при помощи уравнений. Понятие об исследовании задачи
- Применение уравнений к решению задач в общем виде
- Понятие о неравенстве
- Решение неравенств первой степени с одним неизвестным
- Общие сведения о неравенствах
- Определения и свойства
- Строгие и нестрогие неравенства
- Двойное неравенство
- Неравенство с переменной
- Как решать неравенства
- Числовые промежутки
- Числовой луч
- Открытый числовой луч
- Отрезок
- Интервал
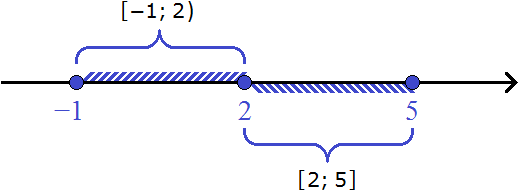
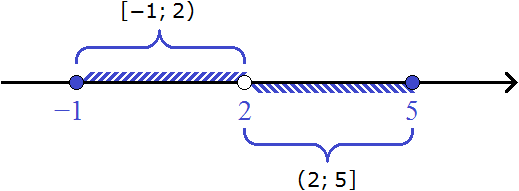
- Полуинтервал
- Изображение числовых промежутков на координатной прямой
- Примеры решения неравенств
- Когда решений нет
- Когда решений бесконечно много
- Задания для самостоятельного решения
Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Числовые неравенства: определение, примеры
При введении понятия неравенства имеем, что их определение производится по виду записи. Имеются алгебраические выражения, которые имеют знаки ≠ , , > , ≤ , ≥ . Дадим определение.
Числовым неравенством называют неравенство, в записи которого обе стороны имеют числа и числовые выражения.
Числовые неравенства рассматриваем еще в школе после изучения натуральных чисел. Такие операции сравнения изучаются поэтапно. Первоначальные имею вид 1 5 , 5 + 7 > 3 . После чего правила дополняются, а неравенства усложняются, тогда получаем неравенства вида 5 2 3 > 5 , 1 ( 2 ) , ln 0 . 73 — 17 2 0 .
Видео:Алгебра 9. Урок 1 - Неравенства. Определения и свойстваСкачать

Свойства числовых неравенств
Чтобы правильно работать с неравенствами, необходимо использовать свойства числовых неравенств. Они идут из понятия неравенства. Такое понятие задается при помощи утверждения, которое обозначается как «больше» или «меньше».
- число a больше b , когда разность a — b – положительное число;
- число a меньше b , когда разность a — b – отрицательное число;
- число a равно b , когда разность a — b равняется нулю.
Определение используется при решении неравенств с отношениями «меньше или равно», «больше или равно». Получаем, что
- a больше или равно b , когда a — b является неотрицательным числом;
- a меньше или равно b , когда a — b является неположительным числом.
Определения будут использованы при доказательствах свойств числовых неравенств.
Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Основные свойства
Рассмотрим 3 основные неравенства. Использование знаков и > характерно при свойствах:
- антирефлексивности, которое говорит о том, что любое число a из неравенств a a и a > a считается неверным. Известно, что для любого a имеет место быть равенство a − a = 0 , отсюда получаем, что а = а . Значит, a a и a > a неверно. Например, 3 3 и — 4 14 15 > — 4 14 15 являются неверными.
- ассиметричности. Когда числа a и b являются такими, что a b , то b > a , и если a > b , то b a . Используя определение отношений «больше», «меньше» обоснуем его. Так как в первой части имеем, что a b , тогда a − b является отрицательным числом. А b − a = − ( a − b ) положительное число, потому как число противоположно отрицательному числу a − b . Отсюда следует, что b > a . Аналогичным образом доказывается и вторая его часть.
Например, при заданном неравенстве 5 11 имеем, что 11 > 5 , значит его числовое неравенство − 0 , 27 > − 1 , 3 перепишется в виде − 1 , 3 − 0 , 27 .
Перед тем, как перейти к следующему свойству, заметим, что при помощи ассиметричности можно читать неравенство справа налево и наоборот. Таким образом, числовое неравенство можно изменять и менять местами.
- транзитивности. Когда числа a , b , c соответствуют условию a b и b c , тогда a c , и если a > b и b > c , тогда a > c .
Первое утверждение можно доказать. Условие a b и b c означает, что a − b и b − c являются отрицательными, а разность а — с представляется в виде ( a − b ) + ( b − c ) , что является отрицательным числом, потому как имеем сумму двух отрицательных a − b и b − c . Отсюда получаем, что а — с является отрицательным числом, а значит, что a c . Что и требовалось доказать.
Аналогичным образом доказывается вторая часть со свойством транизитивности.
Разобранное свойство рассматриваем на примере неравенств − 1 5 и 5 8 . Отсюда имеем, что − 1 8 . Аналогичным образом из неравенств 1 2 > 1 8 и 1 8 > 1 32 следует, что 1 2 > 1 32 .
Числовые неравенства, которые записываются с помощью нестрогих знаков неравенства, обладают свойством рефлексивности, потому как a ≤ a и a ≥ a могут иметь случай равенства а = а . им присуща ассиметричность и транзитивность.
Неравенства, имеющие в записи знаки ≤ и ≥ , имеют свойства:
- рефлексивности a ≥ a и a ≤ a считаются верными неравенствами;
- антисимметричности, когда a ≤ b , тогда b ≥ a , и если a ≥ b , тогда b ≤ a .
- транзитивности, когда a ≤ b и b ≤ c , тогда a ≤ c , а также, если a ≥ b и b ≥ c , то тогда a ≥ c .
Доказательство производится аналогичным образом.
Видео:Профильный ЕГЭ 2023. Математика. Задача 6: все о корнях и степенях. Перезапуск первой частиСкачать

Другие важные свойства числовых неравенств
Для дополнения основных свойств неравенств используются результаты, которые имеют практическое значение. Применяется принцип метода оценка значений выражений, на которых и базируются принципы решения неравенств.
Данный пункт раскрывает свойства неравенств для одного знака строгого неарвенства. Аналогично производится для нестрогих. Рассмотрим на примере, сформулировав неравенство если a b и c являются любыми числами, то a + c b + c . Справедливыми окажутся свойства:
- если a > b , то a + c > b + c ;
- если a ≤ b , то a + c ≤ b + c ;
- если a ≥ b , то a + c ≥ b + c .
Для удобного представления дадим соответствующее утверждение, которое записывается и приводятся доказательства, показываются примеры использования.
Прибавление или вычисления числа к обеим сторонам. Иначе говоря, когда a и b соответствуют неравенству a b , тогда для любого такого числа имеет смысл неравенство вида a + c b + c .
Чтобы доказать это, необходимо, чтобы уравнение соответствовало условию a b . Тогда ( a + c ) − ( b + c ) = a + c − b − c = a − b . Из условия a b получим, что a − b 0 . Значит, ( a + c ) − ( b + c ) 0 , откуда a + c b + c . Множество действительных числе могут быть изменены с помощью прибавления противоположного числа – с .
К примеру, если обе части неравенства 7 > 3 увеличиваем на 15 , тогда получаем, что 7 + 15 > 3 + 15 . Это равно 22 > 18 .
Когда обе части неравенства умножить или разделить на одно и то же число c , получим верное неравенство. Если взять число c отрицательным, то знак поменяется на противоположный. Иначе это выглядит так: для a и b неравенство выполняется, когда a b и c являются положительными числами, то a· c b · c , а если v является отрицательным числом, тогда a · c > b · c .
Когда имеется случай c > 0 , необходимо составить разность левой и правой частей неравенства. Тогда получаем, что a · c − b · c = ( a − b ) · c . Из условия a b , то a − b 0 , а c > 0 , тогда произведение ( a − b ) · c будет отрицательным. Отсюда следует, что a · c − b · c 0 , где a · c b · c . Другая часть доказывается аналогичным образом.
При доказательстве деление на целое число можно заменить умножением на обратное заданному, то есть 1 c . Рассмотрим пример свойства на определенных числах.
Разрешено обе части неравенства 4 6 умножаем на положительное 0 , 5 , тогда получим неравенство вида − 4 · 0 , 5 6 · 0 , 5 , где − 2 3 . Когда обе части делим на — 4 , то необходимо изменить знак неравенства на противоположный . отсюда имеем, что неравенство примет вид − 8 : ( − 4 ) ≥ 12 : ( − 4 ) , где 2 ≥ − 3 .
Теперь сформулируем вытекающие два результата, которые используются при решении неравенств:
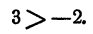
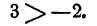
- Следствие 1.При смене знаков частей числового неравенства меняется сам знак неравенства на противоположный, как a b , как − a > − b . Это соответствует правилу умножения обеих частей на — 1 . Оно применимо для перехода. Например, − 6 − 2 , то 6 > 2 .
- Следствие 2.При замене обратными числами частей числового неравенства на противоположный, меняется и его знак, причем неравенство останется верным. Отсюда имеем, что a и b являются положительными числами, a b , 1 a > 1 b .
При делении обеих частей неравенства a b разрешается на число a · b . Данное свойство используется при верном неравенстве 5 > 3 2 имеем, что 1 5 2 3 . При отрицательных a и b c условием, что a b , неравенство 1 a > 1 b может получиться неверным.
Например, − 2 3 , однако, — 1 2 > 1 3 являются неверным равенством.
Все пункты объединяет то, что действия над частями неравенства дают верное неравенство на выходе. Рассмотрим свойства, где изначально имеется несколько числовых неравенств, а его результат получим при сложении или умножении его частей.
Когда числа a , b , c , d справедливы для неравенств a b и c d , тогда верным считается a + c b + d . Свойство можно формировать таким образом: почленно складывать числа частей неравенства.
Докажем, что ( a + c ) − ( b + d ) является отрицательным числом, тогда получим, что a + c b + d . Из условия имеем, что a b и c d . Выше доказанное свойство позволяет прибавлять к обеим частям одинаковое число. Тогда увеличим неравенство a b на число b , при c d , получим неравенства вида a + c b + c и b + c b + d . Полученное неравенство говорит о том, что ему присуще свойство транзитивности.
Свойство применяется для почленного сложения трех, четырех и более числовых неравенств. Числам a 1 , a 2 , … , a n и b 1 , b 2 , … , b n справедливы неравенства a 1 b 1 , a 2 b 2 , … , a n b n , можно доказать метод математической индукции , получив a 1 + a 2 + … + a n b 1 + b 2 + … + b n .
Например, при данных трех числовых неравенствах одного знака − 5 − 2 , − 1 12 и 3 4 . Свойство позволяет определять то, что − 5 + ( − 1 ) + 3 − 2 + 12 + 4 является верным.
Почленное умножение обеих частей дает в результате положительное число. При a b и c d , где a , b , c и d являются положительными числами, тогда неравенство вида a · c b · d считается справедливым.
Чтобы доказать это, необходимо обе части неравенства a b умножить на число с , а обе части c d на b . В итоге получим, что неравенства a · c b · c и b · c b · d верные, откуда получим свойство транизитивности a · c b · d .
Это свойство считается справедливым для количества чисел, на которые необходимо умножить обе части неравенства. Тогда a 1 , a 2 , … , a n и b 1 , b 2 , … , b n являются положительные числами, где a 1 b 1 , a 2 b 2 , … , a n b n , то a 1 · a 2 · … · a n b 1 · b 2 · … · b n .
Заметим, что при записи неравенств имеются неположительные числа, тогда их почленное умножение приводит к неверным неравенствам.
К примеру, неравенство 1 3 и − 5 − 4 являются верными, а почленное их умножение даст результат в виде 1 · ( − 5 ) 3 · ( − 4 ) , считается, что − 5 − 12 это является неверным неравенством.
Следствие: Почленное умножение неравенств a b с положительными с a и b , причем получается a n b n .
Видео:Свойства числовых неравенств. 6 класс.Скачать

Свойства числовых неравенств
Рассмотрим ниже свойства числовых неравенств.
- a a , a > a — неверные неравенства,
a ≤ a , a ≥ a — верные неравенства. - Если a b , то b > a — антисимметричность.
- Если a b и b c то a c — транзитивность.
- Если a b и c — любоое число, то a + с b + c .
- Если a b и c — положительное число, то a · c b · c ,
Если a b и c — отрицательное число, то a · c > b · c .
Следствие 1: если a b , то — a > — b .
Следствие 2: если a и b — положительные числа и a b , то 1 a > 1 b .
- Если a 1 b 1 , a 2 b 2 , . . . , a n b n , то a 1 + a 2 + . . . + a n b 1 + b 2 + . . . + b n .
- Если a 1 , a 2 , . . . , a n , b 1 , b 2 , . . . , b n — положительные числа и a 1 b 1 , a 2 b 2 , . . . , a n b n , то a 1 · a 2 · . . . · a n b 1 · b 2 · . . . b n .
Cледствие 1: если a b , a и b — положительные числа, то a n b n .
Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Уравнения и неравенства в математике с примерами решения и образцами выполнения
Уравнение — это самая простая и самая распространенная форма математической задачи. Заканчивая школьный курс, вы накопили богатый опыт решения разнообразных уравнений. Наступил момент, когда нужно привести свои знания в порядок, разобраться в тех приемах и рассуждениях, которые вы обычно проводили при решении уравнений, часто не обращая внимания на их смысл.
Мы начнем повторение с понятия «выражение».
Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Выражение
Выражение — это числа и буквы, соединенные знаками разнообразных операций.
В начальной школе вы познакомились с простейшими арифметическими операциями — сложением, вычитанием, умножением, делением — и с их помощью составляли выражения такого, например, типа:
Появление новых операций — возведение в степень, логарифмирование, вычисление синуса, тангенса и т. д. — расширило возможности в составлении выражений. Теперь можно составить более сложные выражения, например такие:
Числа и буквы, входящие в состав выражения, имеют разный смысл. Число, как бы оно ни было записано, например 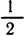
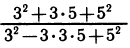
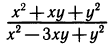
Подставляя в выражение определенные значения букв, мы можем получить числовые выражения, не имеющие смысла. Бессмысленные числовые выражения получаются прежде всего тогда, когда это выражение содержит невыполнимые операции над числами, например деление на нуль, логарифмирование отрицательного числа, арксинус числа, большего единицы, тангенс числа 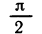
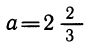
Областью допустимых значений (ОДЗ) выражения обычно называют множество всех значений букв, при подстановке которых выражение имеет смысл, т. е. превращается в осмысленное числовое выражение.
Заметим, что если выражение содержит одну букву, то его ОДЗ — это числовое множество, т. е. какое-то подмножество точек числовой прямой. Если же букв, например, две, то ОДЗ выражения — это множество пар чисел и его можно изобразить в виде области, расположенной на координатной плоскости.
Возьмем какое-либо осмысленное числовое выражение и проделаем все указанные в выражении операции над входящими в него числами. Получим одно число — значение числового выражения. Возьмем буквенное выражение и подставим в него вместо букв числа из ОДЗ (т. е. такие числа, чтобы выражение превратилось в осмысленное числовое выражение). Вычислим значение получившегося числового выражения. Это число называют значением выражения при выбранных значениях букв. Возможность однозначно вычислить значение выражения при любых допустимых значениях входящих в него букв позволяет определить функцию. Вот почему говорят, что выражение можно рассматривать как способ вычисления значений некоторой функции. Поэтому понятие выражения и понятие функции близки между собой.
Два выражения считаются тождественно равными, если равны их числовые значения при любых допустимых значениях букв, входящих в это выражение. Тождество — это два тождественно равных выражения, соединенные знаком равенства.
Во всех приведенных тождествах ОДЗ выражений, стоящих слева и справа, совпадают. Часто используют тождества, соединяющие выражения, имеющие разные ОДЗ. В этом случае имеется в виду, что тождество выполняется на общей части ОДЗ выражений, стоящих справа и слева. Поэтому без дополнительных оговорок считаются тождествами следующие равенства выражений:
Иногда искусственно (какими-либо дополнительными условиями) уменьшается ОДЗ выражений, составляющих некоторое равенство. Тогда можно говорить о тождестве, выполняющемся на некотором множестве. Так, если [х] обозначает целую часть числа х, то равенство 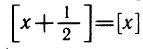
Тождественное преобразование выражения — это переход от одного выражения к тождественно равному выражению.
Самые «безобидные» тождественные преобразования — например, приведение подобных членов, сокращение дробей, использование свойств степени и т. п.— могут привести к выражению, у которого ОДЗ больше или меньше, чем у исходного выражения. Это может оказаться существенным при решении уравнений, поэтому информацию об изменении ОДЗ при тождественных преобразованиях полезно хранить в памяти (собственной-, машинной или просто в тетради).
Видео:Решение неравенства методом интерваловСкачать

Уравнение
Возьмем два числовых выражения и поставим между ними знак равенства. Мы получим числовое равенство. Оно будет верным или неверным в зависимости от того, равны или не равны значения взятых числовых выражений. Классическими примерами являются равенства 2 ⋅ 2 = 4 и «2 ⋅ 2 = 5».
Отметим еще раз, что, когда мы говорим «равенство двух числовых выражений», мы вовсе не утверждаем, что эти два выражения действительно равны. Соединить два числовых выражения A и В знаком « = » и говорить о получившемся равенстве А =В можно независимо от того, верно или неверно сформулированное нами утверждение А = В.
Возьмем два буквенных выражения и соединим их знаком равенства. Получим уравнение. Таким образом, уравнение в первом приближении можно понимать как равенство двух буквенных выражений.
Равенство числовых выражений иногда называют «безусловным» равенством, т. е. равенством или безусловно верным, или безусловно неверным. Уравнение с этой точки зрения можно считать «условным равенством» — при одних условиях ( т. е. при одних значениях букв) оно может оказаться верным, при других — неверным. Тождество — это равенство, верное при всех допустимых значениях букв. Его тоже можно считать частным случаем уравнения.
Уравнение — это не просто формальное равенство двух выражений. Главное в понятии уравнения — это постановка вопроса о его решении. Можно сказать, что уравнение — это равенство двух выражений вместе с призывом найти его решения. Опишем более точно, что же значит решить уравнение.
Буквы, входящие в состав уравнения (т. е. в состав выражений, образующих уравнение), называются неизвестными. Если такая буква одна, то говорят, что мы имеем дело с уравнением с одним неизвестным. Аналогично можно говорить об уравнении с двумя, тремя и любым другим числом неизвестных.
Рассмотрим уравнение с одним неизвестным. Значение неизвестного, при подстановке которого уравнение превращается в верное числовое равенство, называется корнем уравнения.
Решить уравнение с одним неизвестным — значит найти все его корни.
Возьмем уравнение с числом неизвестных, большим чем одно. Например, рассмотрим уравнение с двумя неизвестными. Чтобы получить из него числовое равенство, надо каждому неизвестному придать определенное числовое значение, т. е. взять пару чисел. Решить уравнение с двумя неизвестными — значит найти все пары чисел, удовлетворяющих этому уравнению, т. е. такие, при подстановке которых уравнение превращается в верное числовое равенство. Одну такую пару тоже можно было бы назвать корнем уравнения, но обычно так не говорят, а вводят понятие «решение уравнения».
Винер Норберт
(1894—1964) — американский математик, создатель кибернетики как «науки об управлении и связи в живом организме и машине». Работы Винера являются основополагающими для применения вычислительных машин в различных сферах человеческой деятельности. Норберту Винеру принадлежит высказывание: «Вычислительная машина ценна ровно настолько, насколько ценен использующий ее человек».
Решение уравнения с двумя неизвестными — это пара чисел, удовлетворяющих этому уравнению.
Разумеется, и в случае уравнения с одним неизвестным можно вместо слов «корень уравнения» говорить «решение уравнения». Путаница может возникнуть из-за разного употребления слова «решение». Можно сказать о решении уравнения как его корне. При таком употреблении этого слова имеют смысл такие фразы, как «уравнение имеет одно решение», «уравнение имеет три решения», «уравнение не имеет решений». В речи часто используют словосочетание «решение уравнения» как процесс нахождения его корней (решений). Можно сказать так: «Уравнение имеет сложное решение», «Я не смог найти путь решения этого уравнения». В процессе решения уравнения может обнаружиться, что оно совсем не имеет корней (решений). В этом случае мы скажем, что мы уравнение решили: доказали, что у него решений нет.
Что означает найти корни уравнения? В школьной практике при решении уравнений принято записывать ответ как результат знакомых операций над числами, например:
В то же время при решении прикладных задач бывает необходимо представить ответ в десятичной записи с определенным числом знаков после запятой. Такой ответ можно получить, используя калькулятор или другое вычислительное устройство.
Мы условились понимать под уравнением равенство, составленное из двух выражений. Мы уже говорили о том, что выражение можно рассматривать как способ задания некоторой функции. Поэтому уравнение можно понимать как равенство, соединяющее две функции. Пусть даны две функции от переменной х, например y = f(x) и y = g<x). Составим уравнение f<x) = g(х). Оно получено приравниванием выражений f (х) и g (х). Пусть D1 =D (f) и D2 = D (g) — области определений функций f и g. Тогда D1 и D2 можно понимать как области допустимых значений выражений f (х) и g (х). Общая часть областей D1 и D2, т. е. множество 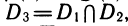
Полезно вспомнить, что подставлять в уравнение можно любое значение х. При каком-то значении х может получиться бессмысленное числовое выражение, а при х из ОДЗ получится осмысленное числовое равенство. Если при этом оно окажется еще и верным, то взятое число х является корнем уравнения.
Вернемся к вопросу о решении уравнения. Начнем с уравнения с одним неизвестным х. В какой форме рекомендуется записывать его ответ?
Уравнение может иметь один корень, например x=5. Тогда ответ проще всего записать именно в этой форме: х=5.
Уравнение может иметь несколько (конечное число) корней. Ответ удобно записать в виде перечисления всех корней, давая каждому значению х свой номер. Например, х1 = — 1, x2 = 0, xз=1. Полезно корни располагать в порядке возрастания.
Уравнение может вовсе не иметь корней. В таком случае нагляднее всего это и указать в ответе словами: корней нет.
Тригонометрические уравнения (и вообще уравнения с периодическими функциями) часто имеют бесконечно много корней, которые можно записать в виде одной или нескольких последовательностей. Скажем, возможна такая запись ответа:
Встречаются уравнения, решения которых заполняют один или несколько промежутков, которые и указываются в ответе, например: 0 ≤ x ≤ 1 или х —- любое число.
Все корни (решения) уравнения образуют множество корней. Слово «множество» не означает, что корней очень много («великое множество»). Если множество корней обозначить одной буквой, скажем X, то ответ может быть записан иначе. Примеры записи ответов с употреблением теоретико-множественных обозначений: Х=; Х = ; Х= ∅ (пустое множество, т. е. корней нет; не надо путать знак пустого множества с обозначением нуля);
Множество решений уравнения с двумя неизвестными состоит из пар значений этих неизвестных. Важно помнить, что одна пара, скажем х=1, у = 5,— это одно решение (а не два).
Равносильность
Если идет дождь, то мы открываем зонт. Можно сказать, что открывание зонта является следствием того, что идет дождь. Если число делится на 6, то оно четно. Так же как и в первом случае, можно сказать, что четность числа является следствием его делимости на 6.
Пусть даны два уравнения Лий. Если каждый корень уравнения А является корнем уравнения В, то говорят, что уравнение В является следствием уравнения А, и записывают так: А ⇒ В (читается: «Из А следует В», или «В является следствием A», или «Если А, то В»),
На языке теории множеств можно сказать короче: уравнение В является следствием уравнения А, если множество корней уравнения А содержится в множестве корней уравнения В, т. е. если XA ⊂ ХВ, где ХА и Хв — упомянутые множества корней.
Переходя от одного уравнения к его следствию, мы не потеряем корней исходного уравнения, но возможно приобретем лишние. Основой получения разнообразных следствий является следующее простое соображение. Пусть а = b — числовое равенство, a f — функция, определенная в точках а и b. Тогда равенство f(a) = f(b) является следствием равенства а = b, т. е. если равенство а — b верно, то верно и равенство f(a) = f(b) (если оно имеет смысл).
Возьмем теперь уравнение, полученное приравниванием двух выражений. Если функция f определена при всех значениях этих выражений, то, вычислив значения функции f от обеих частей уравнения, получим новое уравнение, являющееся следствием исходного. Это правило особенно удобно, если функция f определена при любых числовых значениях переменных.
Приведем примеры. Возьмем уравнение
Следующие уравнения являются его следствиями (рядом записана применяемая функция, а буквой z обозначен ее аргумент):
Все функции f определены при любом z, поэтому получение указанных следствий было формальной операцией.
В случаях 5—8 функции уже определены не при всех х. Однако во всех случаях новые уравнения являются следствиями исходного. Этот вывод уже не является формальным. Примеры 5—7 разберите самостоятельно. Пример 8 является существенно более трудным и требует дополнительных сведений о корнях исходного уравнения (докажите, что все его корни лежат на отрезке [0; 1]).
Два уравнения называются равносильными, если каждое из них является следствием другого, т. е. если каждый корень одного из них является корнем другого. Пусть уравнение А имеет множество корней ХА, а уравнение В — множество Хв. Равносильность уравнений А и В обозначается так: А ⇔ В. По определению равносильность означает выполнение двух условий: А ⇒ В (уравнение В является следствием уравнения А) и В ⇒ А (наоборот, уравнение А является следствием уравнения В). На языке теории множеств равносильность означает равенство ХА = ХВ.
Итак, у равносильных уравнений корни одни и те же. Поэтому основным способом решения уравнения является следующий: с помощью перехода от одного уравнения к равносильному стараются прийти к уравнению, решения которого находятся легко.
Основной способ получения следствия нам известен — вычисление значений какой-либо функции от обеих частей уравнения.
Чтобы этот переход сохранял равносильность, надо, чтобы возможен был обратный переход. Это всегда выполняется, если новое уравнение получено с помощью функции, имеющей обратную. На этом соображении основаны теоремы о равносильности, позволяющие утверждать равносильность пар уравнений, получающихся друг из друга с помощью взаимно обратных функций. Сформулируем несколько таких теорем.
Запишем уравнение в символической форме:
□ = Δ,
где □ и Δ —два выражения, составляющие уравнение.
Теоремы помещены в левой колонке таблицы. В правой колонке указаны взаимно обратные функции, с помощью которых эти теоремы доказываются.
Во всех этих случаях не было трудностей с областями определения применяемых функций. Использование таких распространенных операций, как возведение в квадрат, умножение и деление на некоторую функцию, нахождение обратной величины и т. д., в общем виде не гарантирует равносильности. Например, возводя в квадрат обе части уравнения, мы получаем следствие:
Вообще говоря, обратный переход неверен. Однако если из последующего решения уравнения □2= Δ2 мы узнаем, что для его корней выражения □ и Δ имеют одинаковый знак, то можно будет поставить стрелку в обратном направлении и найти корни исходного уравнения:
□2 = Δ2 ⇒ □ = Δ, если □ и Δ одного знака.
Остановимся подробнее на некоторых полезных преобразованиях уравнений.
1) Тождественное преобразование одной из частей уравнения и перенос членов из одной части уравнения в другую с противоположным знаком приводят к равносильному уравнению, если при этом не происходит изменения ОДЗ. Например, уравнение
x 2 — Зх + 2 = 0.
В то же время уравнения
не являются равносильными (корни первого: х1 = — 8, x2 = 4; корень второго: x = 4), так как логарифмирование произведения уменьшило ОДЗ.
2) Переход к совокупности уравнений. Рассмотрим задачу, в которой требуется решить несколько уравнений, а затем объединить их корни. Можно сказать, что идет речь о решении совокупности уравнений. Обычно совокупность обозначается с помощью прямой скобки.
Пусть ОДЗ выражений □ и ∆ совпадают. Тогда уравнение □ • ∆ = 0 равносильно совокупности
Оговорка про совпадение ОДЗ не случайна. Так, уравнение cos x • tg x = 0 не равносильно совокупности
3) Переход к системе уравнений. Рассмотрим задачу, в которой надо решить несколько уравнений и взять их общие корни (или иначе найти числа, удовлетворяющие каждому из уравнений системы). В систему можно объединять не только уравнения, но и различные условия, ограничения, неравенства. Например, решить систему
означает, что надо решить первое уравнение и взять только те его корни, для которых выполняется неравенство х+1;>0.
Использование переходов от уравнения к совокупностям и системам позволяет разнообразить схемы равносильных переходов. Покажем некоторые из них:
Различные переходы от уравнения к совокупностям и системам изображены на схеме XV.
Видео:Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Неравенство
Почти все, что было выше сказано об уравнении, можно дословно перенести и на неравенство. Прежде всего отметим, что знаков неравенства четыре: > (больше),
Приведем основные правила преобразования неравенств, используя знак следствия ⇒ и равносильности ⇔.
Основой техники преобразования неравенств является следующее общее соображение: пусть функция f монотонна на промежутке, содержащем числа а и b. Тогда а f (b) если f строго убывает.
Указанные выше свойства 3—6 получаются применением этого правила к функциям y = cz и 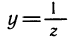
Аналогично для функций y = z2 и у = 2z можно записать:
Неравенство с одним неизвестным получается, когда соединяют знаком неравенства два выражения, содержащие одну букву, или, что близко по смыслу, две функции от одной и той же переменной. Аналогично можно рассматривать неравенства с двумя и более неизвестными.
Ограничимся неравенствами с одним неизвестным. Область допустимых значений (ОДЗ) неравенства—это множество значений неизвестного, при подстановке которых получается осмысленное числовое неравенство. Решение неравенства — это такое значение неизвестного, при подстановке которого получается верное числовое неравенство. Решить неравенство — это значит найти, описать множество его решений. Два неравенства называются равносильными, если множества их решений совпадают. Одно неравенство является следствием другого, если множество его решений содержит в себе множество решений второго. Ясно, что каждое из равносильных неравенств является следствием другого. Технику решения неравенств с помощью переходов, сохраняющих равносильность.
Параметр
Посмотрим на знакомое уравнение аx 2 + bх+с = 0. Выражение, стоящее в его левой части, содержит четыре буквы — х, а, b, с. Хотя все эти четыре буквы равноправны, мы смотрим на это уравнение как на квадратное уравнение относительно неизвестного х, считая а, b, с буквенными коэффициентами, параметрами. Необходимость рассматривать уравнения с буквенными коэффициентами возникает часто. Прежде всего это полезно тогда, когда формулируются некоторые общие свойства, присущие не одному конкретному уравнению, а целому классу уравнений. Так, мы можем сформулировать свойства корней квадратного уравнения, показательного уравнения ах = b, тригонометрического уравнения sin ωх=а в зависимости от параметров a, b, ω.
Разумеется, то, что в уравнении одни буквы мы считаем неизвестными, а другие — параметрами, в значительной степени условно. В реальной практике из одного и того же соотношения между переменными приходится выражать одни переменные через другие, т. е. решать уравнение относительно одной буквы, считая ее обозначением неизвестного, а другие буквы параметрами.
По традиции неизвестные обозначаются последними буквами латинского алфавита — х, у, z, а параметры — первыми — а, b, с или вообще буквами другого алфавита (например, греческими).
При решении уравнений и неравенств с параметрами чаще всего встречаются две задачи:
- Найти формулы для решений уравнения (неравенства), выражающие эти решения как функции от параметров. Типичный пример — формула корней квадратного уравнения.
- Исследовать решения уравнения (неравенства) в зависимости от изменения значений параметров. Скажем, встречается такая задача: найти число корней уравнения в зависимости от параметра или определить, при каких значениях параметра уравнение не имеет корней. Очень часто исследование корней в зависимости от параметра можно провести, не вычисляя самих корней.
Пример:
Дано уравнение x 2 + 2x + а = 0 относительно неизвестного х с параметром а.
- 1) При каких значениях а уравнение имеет два корня?
- 2) При каких значениях а уравнение имеет два корня, причем один из них больше единицы, а другой меньше?
- 3) При каких значениях а сумма квадратов корней меньше шести?
Решите этот пример самостоятельно.
Укажем ответы: 1) а Уравнения с одним неизвестным
В простейших случаях решение уравнения с одним неизвестным распадается на два шага — преобразование уравнения к стандартному и решение стандартного уравнения. Второй шаг осуществляется по известным формулам, которые всегда можно восстановить в памяти с помощью справочников. Есть они и в справочных материалах в нашем учебнике.
Перечислим стандартные уравнения, которые были нами изучены.
- Линейное уравнение ах+b = 0.
- Квадратное уравнение аx 2 + bх + с=0.
- Простейшее степенное уравнение хп = а.
- Показательное уравнение а’ = b.
- Логарифмическое уравнение logax = b.
- Простейшие тригонометрические уравнения sin x = a, cos x=a, tg х=а, ctg x — a.
Преобразование уравнения к одному из стандартных является основным шагом в решении уравнения. Полностью алгоритмизировать процесс преобразования нельзя, однако полезно запомнить некоторые наиболее употребительные приемы, общие для всех типов уравнений.
1) Разложение на множители. Если уравнение равносильными преобразованиями удается привести к виду □ • ∆ =0, то, как мы уже отмечали, исходное уравнение равносильно совокупности двух более простых уравнений 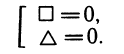
Этот прием часто применяется при решении алгебраических уравнений степени выше второй, при решении тригонометрических уравнений. Соответствующие примеры будут приведены ниже.
2) Введение нового неизвестного. Посмотрите, не решая, на следующий набор уравнений:
В каждом из этих уравнений отметим присутствие выражения x 2 +Зх. Если заменить его буквой у, т. е. положить у = x 2 +3x то получим более простые уравнения относительно у:
Найдя из этих уравнений значения у, подставим их в соотношение у = x 2 + 3х и вычислим корн и исходного уравнения.
3) Графический метод. Рассмотрим уравнение с одним неизвестным f(x) = g(x).
Изобразим на одном рисунке графики функций y = f(x) и y = g(х) (рис. 139). Точкам пересечения графиков этих функций соответствуют те значения аргумента х, при которых совпадают значения функций, т. е. корни данного уравнения.
Итак, абсциссы точек пересечения графиков функций y = f(x) и y = g(x) являются корнями уравнения f(x) = g(x).
Например, для уравнения x 2 = х+2 такими точками будут Р1 (—1; 1) и Р2 (2; 4), т. е. x1 = -1, x2 = 2.
Если уравнение имеет вид f (х) = 0, то в качестве функции, стоящей в правой части, выступает функция у = 0. Графиком ее будет ось х, поэтому корнями уравнения f(x) = 0 будут абсциссы точек пересечения графика функции y=f(x) с осью х.
Графическая иллюстрация решения уравнения указывает на первый взгляд и способ решения уравнения: строят в системе координат две кривые и находят их точки пересечения. Действительно, если выбрать масштаб и построить графики достаточно аккуратно, то можно приближенно найти точки пересечения и их абсциссы — корни уравнения. Но для того чтобы найти координаты точек пересечения точно, как раз и нужно решить соответствующее уравнение! В то же время графическая иллюстрация часто дает некоторые качественные ответы, число корней, а также грубо указывает отрезки на числовой оси, где эти корни могут находиться. Рассмотрим в качестве примера уравнение
Построим графики функций, стоящих в левой и правой частях.
Из рисунка 140 можно заключить, что уравнение имеет два корня, один из которых находится в интервале (0; 1), а другой — в интервале (2; 3). Можно указывать эти интервалы и более точно: (0; 0,5) и (2; 2,5), еще более точно: (0,2; 0,3) и (2,2; 2,3). (Действительно, нетрудно проверить, что при х = 0,2 имеем 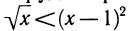
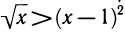
Вообще, вычисляя и сравнивая значения левой и правой частей уравнения, можно найти корни с любой степенью точности.
Корни уравнения пятой степени х5—Зх + 1= 0 вообще нельзя записать с помощью радикалов, но, построив достаточно точный график функции у = х5-Зх+1 (рис. 141), можно определить, что уравнение имеет три корня в интервалах (—1,5; —1,3), (0; 0,5) и (1; 1,3).
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Примеры решения уравнений
1) Алгебраическое уравнение x (x+ 1) (x + 2) (x + 3)= 120.
Если раскрыть скобки и привести подобные члены, то получится уравнение четвертой степени. Общий прием решения уравнения четвертой степени нам неизвестен, поэтому не будем торопиться раскрывать скобки.
Первый способ. Воспользуемся симметрией левой части. Перемножим первый и четвертый множители, а также второй и третий. Получим ( x 2 + Зх) ( x 2 + Зх + 2) = 120. Теперь видно, что после замены x 2 + 3х = у уравнение сводится к квадратному y (y+ 2)= 120.
Второй способ. Симметрией можно воспользоваться иначе. Заметим, что числа х, х+l. х+2, х + З расположены на числовой оси симметрично относительно числа 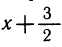
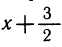
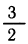
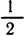
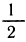
,x + 3 = у +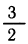
Теперь преобразования более очевидны:
Это так называемое биквадратное уравнение, приводящееся к
квадратному заменой y2 = z
Третий способ. Перемножив все скобки, получим уравнение
Попробуем подобрать корень.
Легко догадаться, что 2 • 3 • 4 • 5= 120, поэтому х=2 является корнем. Разделим левую часть уравнения на х — 2:
Теперь подбираем корень уравнения x3 + 8x 2 + 27x + 60 = 0. Можно угадать х= — 5 (так как ( — 5) • ( — 4) • ( — 3) • ( — 2)= 120). Выделим множитель x+ 5:
У оставшегося квадратного трехчлена x 2 + Зx+12 вещественных корней нет.
Четвертый способ. Он основан на тождестве х(х+ 1)(х + 2)(х + 3)+1 =( x 2 + 3x+1) 2 (см. задачу 3 в конце главы). Получаем:
2) Уравнение с модулем | x 2 + 2x|+ x 2 + x = 5.
Уравнение равносильно совокупности двух систем:
Рекомендуем сначала решить квадратное неравенство
Ответ:
3) Иррациональное уравнение
Уравнение равносильно системе 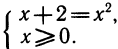
4) Показательное уравнение
Замена 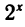
При потенцировании теряется информация об ОДЗ. Поэтому выпишем ОДЗ в явном виде:
Решением этой системы неравенств будет интервал (1; 3). Теперь потенцируем, перенося логарифм в левую часть:
Подобрав один корень х = 2, выделяем множитель (x— 2):
Корни квадратного множителя: х=1±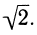
6) Тригонометрическое уравнение
и получаем уравнение
т. е. 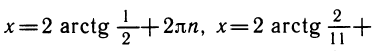
Так как уравнение несовместно с условием cos х= — 1, то при переходе к тангенсу половинного угла потери корней не произошло.
Приближенные методы вычисления корней
Во многих случаях при решении уравнений их корни находят приближенно. Для этого в математике накоплены различные методы приближенных вычислений. Обычно они дают последовательность приближений к искомому числу. Примером может служить способ извлечения квадратного корня, знакомый из курса алгебры.
Простейшим методом приближенного вычисления корней является метод половинного деления. Допустим, что известен промежуток [а; b], на котором лежит искомый корень. Приближенно строится график функции f на этом промежутке (например, так, как это изображено на рисунке 142).
Вычисляя f (а) и f (b), видим, что эти числа разных знаков: f (а) 0. Вычисляем далее значение функции f в середине отрезка [а; b). Из двух половин отрезка [a; b] берем ту, на концах которой знаки функции различны. Очевидно, корень х лежит внутри нового отрезка. Совершаем с ним ту же процедуру: делим его пополам, вычисляем значение функции f в точке деления и берем ту половину отрезка, на концах которой знаки функции f различны. Так мы получим последовательность отрезков, длина которых убывает и внутри которых лежит искомый корень. Это и означает, что получена последовательность приближенных значений искомого корня.
И. Ньютону принадлежит так называемый метод касательных. Об этом способе приближенного вычисления корней можно получить представление, рассматривая рисунок 143. Приближенные значения корня получаются построением касательных к графику функции. Уравнение касательной написать нетрудно, а затем нужно найти точку ее пересечения с осью х, что и дает приближенное значение корня функции.
Вместо касательных можно проводить хорды (рис. 144) и поступать аналогично (метод хорд).
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Неравенства с одним неизвестным
Решение неравенств (так же как и решение уравнений) обычно распадается на два шага — преобразование неравенства к одному из стандартных и решение стандартного неравенства. К стандартным неравенствам мы отнесем следующие типы неравенств, изученные нами ранее (из возможных четырех знаков неравенства мы выбираем один):
- Линейное неравенство ах + b> 0.
- Квадратное неравенство а x2+ bх + с>0.
- Степенное неравенство
>а.
- Показательное неравенство
>Ь.
- Логарифмическое неравенство logах>Ь.
Решение стандартных неравенств было рассмотрено нами в предыдущих главах.
Общие приемы решения уравнений и неравенств аналогичны. Так же как и для уравнений, при решении неравенств помогает разложение на множители. Как уже отмечалось, решение неравенства вида 
неравенств:
В то же время если множители □ или ∆ являются линейными или произведениями линейных, то не стоит сводить решение неравенства к системе: проще применить метод интервалов, который сильно сокращает количество вычислений.
Важнейшим методом решения неравенств является метод замены неизвестного. Мы проиллюстрируем его примером решения неравенства
Прежде всего сделаем замену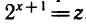
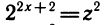
Изобразим график квадратного трехчлена y = 2z 2 — 16z (рис. 145). Решением неравенства |у + 19| ≤ 5, как видно из графика, является объединение двух отрезков [z1, z2] и [z3, z4], где z1, z4 — решения уравнения у= = — 14, a z2 , z3 — решения уравнения y = —24. Решая эти уравнения, находим z1 = 1, z2 =2, z3 = 6, z4 = 7. Учитывая, что функция z является возрастающей, решаем стандартные неравенства и записываем ответ: [—1; 0]U[log2 6 —1; log2 7—1].
Видео:Основные свойства числовых неравенств - алгебра 9 классСкачать

Примеры решения неравенств
1) Алгебраическое неравенство
Перенесем правую часть влево, приведем к общему знаменателю и разложим на множители числитель дроби:
Применяя метод интервалов, с помощью числовой оси (рис. 146) решаем неравенство и получаем ответ: х 1.
2) Иррациональное неравенство
ОДЗ: х + 2 ≥ 0 ⇔ х ≥ — 2.
Если иррациональное уравнение мы смело возводили в квадрат, так как всегда можно было проверить нарушение равносильности, подставляя корни полученного уравнения, то при решении неравенства нужно поступать аккуратнее.
Заметим, что неравенство а>b, где а ≥ 0, b
Корни квадратного трехчлена x1 = — 1, x2 = 2 наносим на числовую ось; решением неравенства будут числа 0 ≤ х 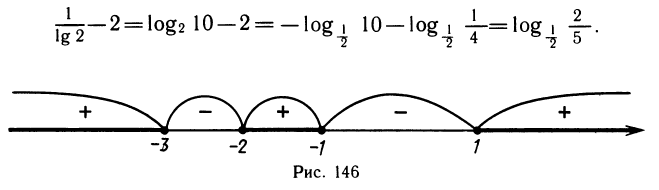
Стандартное логарифмическое неравенство 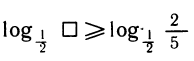
Решаем каждое неравенство системы методом интервалов, предварительно сделав преобразования:
Корни числителя: x1 = 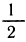
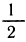
Системы уравнений появляются при решении задач, в которых неизвестной является не одна величина, а несколько. Эти величины связаны определенными зависимостями, которые записываются в виде уравнений.
Способ подстановки
Если система имеет хотя бы одно решение, она называется совместной. Если решений у системы нет, она называется несовместной. Слово «несовместность» наглядно показывает, что уравнения системы накладывают несовместимые друг с другом условия, которым должны удовлетворять неизвестные. Например, система 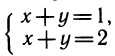
Одним из основных способов решения систем является способ подстановки. Рассмотрим, например, систему двух уравнений с двумя неизвестными хну. Часто удается одно уравнение преобразовать так, чтобы одно неизвестное явно выражалось как функция другого. Тогда, подставляя его во второе уравнение, мы получим уравнение с одним неизвестным. Приведем примеры.
В каждой из четырех систем второе уравнение системы можно решить относительно у, т. е. преобразовать к виду y = f(x):
Подставляя y = f(x) в первое уравнение системы, получим уравнение с одним неизвестным:
Решая уравнение, находим его корни — значения неизвестного х, а затем для каждого из них находим соответствующее значение у по формуле y = f(x):
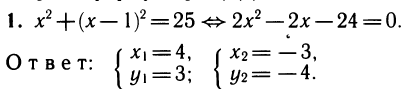
Уравнение имеет четыре корня, а система — четыре решения:
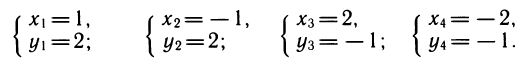
Способ подстановки возможен не всегда, а кроме того, не всегда выгоден и тогда, когда возможен. Часто из уравнений системы удается получить новое уравнение — их следствие — более простого вида. Так, в четвертом из рассматривавшихся выше примеров можно, исключив произведение ху, стоящее справа, получить:
Последнее соотношение является линейным, и из него соотношение между х и у легче находится так: у = 2х.
Важным приемом, часто позволяющим упростить систему, является замена неизвестных. Так, во втором примере полезно заменить x 2 на z и получить более простую систему:
Системы двух уравнений с двумя неизвестными и их решения можно изобразить графически на координатной плоскости. На рисунке 148 изображены кривые уравнений написанных выше систем. Точки пересечения кривых (а точнее, их координаты) — решения систем.
Есть некоторые типы систем, для которых известны стандартные методы решения. Рассмотрим два из них: симметричные системы и линейные системы.
Симметричные системы
Симметричными называются системы, составленные из выражений, являющихся симметричными относительно всех неизвестных. Приведем примеры различных симметричных выражений для двух неизвестных: х и у.
Решение простейшей симметричной системы 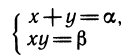
Итак, для решения простейшей симметричной системы надо составить квадратное уравнение с заданными суммой и произведением корней и решить его. Найденные корни будут значениями х и у.
Составляем квадратное уравнение t 2 —3t —4 = 0, откуда t1 = 4, t2 = — 1.
Решение других симметричных систем основано на том, что всякое симметричное относительно х и у выражение можно выразить через u= х+у и v=xy.
Приведем примеры таких выражений:
Делая в симметричной системе замену х+у=u, xy = v, получаем более простую систему относительно и и и, а затем, найдя численные значения и и у, приходим к решению простейших симметричных систем:
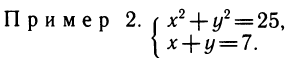

Воспользуемся найденным выше выражением х 3 + у 3 через и и у:
Из второго уравнения v= — 1— u 2 подставляем в первое:
Далее решаем систему
Линейные системы
С системами линейных уравнений мы встречались ранее. В основном рассматривались системы двух линейных уравнений с двумя неизвестными вида
Исследование этой системы можно повторить по информационной схеме XVI.
В практике встречаются системы линейных уравнений с большим количеством неизвестных. Так, в задачах математической экономики можно найти системы, состоящие из нескольких сотен уравнений с таким же примерно числом неизвестных. Для их решения разработаны мощные машинные методы. Эти методы в основном имитируют знакомый вам метод подстановки, которым в принципе можно решить любую такую систему. Основную роль при этом играют компактные способы записи систем и их преобразований. Представьте только себе: система из тысячи уравнений с тысячью неизвестными содержит миллион коэффициентов.
Рассмотрим более скромный пример — систему трех линейных уравнений с тремя неизвестными:
Будем решать систему методом исключения неизвестных. Чтобы исключить х из второго и третьего уравнений, надо вычесть из них первое, умноженное соответственно на 2 и на 3.
Удобно умножить второе и третье уравнения на (—1), а затем из третьего уравнения вычесть второе, умноженное на 5. Получим «треугольную» систему
Из последнего уравнения находим z=1. Подставляя в предыдущее уравнение, находим у=9— 10= — 1.
Подставляя 2=1, у= — 1 в первое уравнение, получим х + 2( — 1) + 3 •1=2, откуда х=1.
Ответ: х— 1, у= — 1, 2=1.
Показанный на этом примере способ решения линейной системы называется методом Гаусса по имени великого немецкого математика, жившего в первой половине XIX в. Метод Гаусса с различными модификациями используется при решении линейных систем с помощью вычислительных машин.
Видео:ТОП-5 ОШИБОК в математике | Математика | TutorOnlineСкачать

Тождества
Мы определили тождество как равенство двух выражений, справедливое при всех допустимых значениях букв, входящих в эти выражения. Такая точка зрения свойственна теории функций — мы рассматриваем две части равенства как функции и называем эти части тождественно равными, если они совпадают как функции, т. е. если они при одних и тех же значениях аргумента принимают равные значения. Возможна другая точка зрения на тождества, которая более тесно связана с алгеброй.
Колмогоров Андрей Николаевич
(1903—1987) — советский математик, один из создателей и автор общепринятой системы аксиом современной теории вероятностей. Автор глубоких идей и результатов в топологии, математической логике, гидродинамике и небесной механике.
«Обобщение понятия часто бывает полезно для постижения его сущности».
В алгебре многочлен рассматривается не как функция, а как некоторое формальное выражение, составленное из одночленов. Мы умеем совершать различные операции над многочленами, не задумываясь при этом над тем, какие значения можно подставлять в многочлен вместо букв. В алгебре два многочлена равны, если после приведения подобных членов окажется, что они составлены из одинаковых одночленов, т. е. если выполняется формальное, почленное равенство. Так, проверяя тождество а 3 — b 3 =(a-b)(a 2 + ab+b 2 ), мы совсем не занимаемся подстановкой в обе части значений а и b (тем более что неясно, сколько их надо подставлять), а преобразуем правую часть и убеждаемся, что она формально совпадает с левой.
Проверке формального совпадения многочленов может помочь их запись, принятая в качестве стандартной. Например, если многочлены от одной буквы х записывать по убывающим степеням (как мы привыкли), то тождество многочленов будет означать равенство их степеней и совпадение коэффициентов, стоящих на одинаковых местах.
Возникает естественный вопрос: как связаны между собой функциональное и алгебраическое определения тождества? Разумеется, если два многочлена равны формально, то они принимают одинаковые значения при всех значениях букв. Обратное заключение составляет содержание трудной теоремы алгебры — теоремы о тождестве. Поясним смысл этой теоремы для простейшего случая многочленов от одной буквы х.
Прежде всего заметим, что от равенства f(x)=g(x) всегда можно перейти к равенству f(x) — g (х)=0, как бы мы ни определяли понятие тождества. Это означает, что теорему о тождестве можно доказывать в таком упрощенном варианте: если многочлен F (х) при всяком значении x равен нулю, то этот многочлен нулевой, т. е. не содержит ни одного ненулевого одночлена. Если многочлен F (х) имеет степень n, то, оказывается, достаточно подставлять лишь n + 1 значение х. Иными словами, если многочлен F (х) степени n имеет n + 1 корень, то этот многочлен нулевой. В такой формулировке теорема допускает уже не очень сложное доказательство.
Итак, полезно запомнить, что ненулевой многочлен не может иметь корней больше, чем его степень. Возможна другая формулировка: если два многочлена степени n совпадают в n + 1 точке, то эти многочлены формально равны. Последняя формулировка очень полезна при доказательстве различных тождеств (см. задачи).
В применении к многочленам первой степени нам знакома геометрическая формулировка этой теоремы: через две точки проходит только одна прямая. Аналогично для совпадения двух квадратных трехчленов достаточно равенства их значений в трех точках.
Кроме равенства многочленов, можно определить равенство дробей с алгебраической точки зрения: две дроби 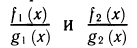
В более усложненном варианте алгебраический подход возможен и к тригонометрическим тождествам. Так, тождествам, содержащим степени sin х и cos х, можно придать условный характер: доказать тождество, используя из тригонометрии лишь соотношение sin 2 x+cos 2 х= 1. Такую задачу можно решить, делая лишь алгебраические преобразования и не вспоминая о том, что такое синус и косинус. Приведем пример условного тождества в алгебре:
Другие примеры условных тождеств приведены в задачах.
Видео:✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

Доказательство неравенств
Наряду с тождествами — равенствами, выполняющимися тождественно,— существуют тождественно выполняющиеся неравенства, т. е. неравенства, верные при любых допустимых значениях входящих в них букв. Приведем простейшие примеры таких тождественно выполняющихся неравенств.
2) а 2 + f 2 + с 2 ≥ 0, причем равенство нулю возможно лишь при а = b = с = 0;
3) х 2 + + q>0, если p 2 — 4q
Последнее неравенство всегда верно, следовательно, всегда верно исходное.
Полученное неравенство (его называют неравенством о среднем арифметическом и среднем геометрическом двух чисел) можно применять к доказательству других неравенств. Убедитесь, например, что следующие неравенства являются следствиями доказанного:
Использование производной дает мощный способ доказательства неравенств с одной переменной. Этот способ основан на следующем соображении: если в точке Хо выполняется условие f (хо) ≥ 0 и для всех х ≥ хо выполняется условие f (х) ≥ 0, то для всех х ≥ хо верно неравенство f(x)>0 (разберитесь в справедливости сформулированного правила).
Пример (неравенство Бернулли).
Для доказательства рассмотрим функцию y = f(x), где f(x) = (1+x) k — l — kx. Имеем f(0) = 0, f'<x) = k<1+x) k-1 — k = k ((1+x) k-1 —1). Так как x ≥ 0, k ≥ 1, то (1+x) k-1 ≥ 1 и f (х) ≥ 0. Значит, при х ≥ 0 функция f возрастает и при всяком х ≥ 0 имеем f(x) ≥ f(0) = 0, что и требовалось доказать.
Видео:Основные свойства уравненийСкачать

Алгебраические уравнения
Алгебраическое уравнение — это уравнение вида
Число n называется степенью уравнения. Уравнение первой степени (или линейное уравнение) решается с помощью арифметических операций. Формула для решения уравнения второй степени (или квадратного уравнения) известна с глубокой древности. В нее входит операция извлечения квадратного корня. Решение уравнения произвольной степени в течение многих веков считалось основной задачей алгебры.
Постановка вопроса о решении алгебраического уравнения может быть различной. Почему «не решается» данное нам уравнение? Рассмотрим возможные ответы на этот вопрос.
1) Нам «не хватает» имеющихся чисел. Уравнение х 2 + 2х + 5 = 0 не имеет вещественных корней. Можно, конечно, на этом утверждении остановиться. Однако полезно, как это было сделано еще в XVI в., ввести комплексные числа, с которыми вы немного знакомы. Комплексное число имеет вид a+bi, где а и b —’ вещественные числа, а символ i (мнимая единица) обозначает такое число, для которого i 2 = — 1. Комплексные числа x1 = — 1 — 2i и x2 = — 1 + 2i являются корнями написанного выше квадратного уравнения.
Если мы разрешим числу х принимать не только вещественные, но и комплексные значения, то отпадет вопрос существования корня алгебраического уравнения. В 1831 г. Гаусс доказал замечательную теорему, которую часто называют основной теоремой алгебры: всякое алгебраическое уравнение имеет хотя бы один комплексный корень.
2) Мы не можем разложить левую часть уравнения на множители. Возьмем, например, уравнение х 5 + x + 1 =0. Не сразу бросается в глаза, что левую часть можно разложить на множители:
После разложения на множители получим уравнения меньших степеней: x 2 + х + 1 = 0 и x 3 — x 2 + 1=0. Однако этот прием проходит далеко не всегда. Так, многочлен х 5 — х+1 уже нельзя разложить на множители с целыми коэффициентами. Известен алгоритм, который позволяет разложить любой многочлен с целыми коэффициентами на множители с целыми коэффициентами, если это возможно. Частный случай применения этого алгоритма мы неоднократно использовали: если многочлен х n + аn-1 х n-1 + … + а0 с целыми коэффициентами имеет множитель вида х — с, где с — целое число (являющееся, конечно, корнем многочлена), то свободный член а0 делится на с. Эта теорема позволяет перебором делителей свободного члена и проверкой найти целые корни многочлена с целыми коэффициентами.
3) Мы не знаем общей формулы для корней уравнения. Простая формула корней квадратного уравнения вызывала желание математиков найти формулы корней уравнения более высокой степени. В XVI в. эта задача была решена для уравнений 3-й и 4-й степеней. Хотя эти формулы громоздки и не употребляются для реального вычисления корней, принципиальное их значение велико: они позволяют записать корни уравнений 3-й (и 4-й) степеней как некоторую функцию от коэффициентов этих уравнений. Эта функция содержит операции извлечения корней 3-й (и 4-й) степеней. Долго изучавшийся вопрос о том, существует ли формула, выражающая корни уравнения 5-й степени через его коэффициенты с помощью радикалов, получил отрицательное решение в работах Абеля (1802—1829) и Галуа (1811 —1832) в начале XIX в.
Итак, как правило, для алгебраического уравнения высокой степени мы не можем указать общей формулы его корней. Для приближенного вычисления корней используют методы анализа.
Различные приближенные методы нахождения корней уравнения часто используют следующее соображение, которое мы неоднократно отмечали раньше: если на концах промежутка функция y=f(х) принимает значения разных знаков, то внутри этого промежутка уравнение f(х) = 0 имеет корень (рис. 142). Это утверждение верно для всех непрерывных функций. С его помощью нетрудно, например, доказать, что всякий многочлен нечетной степени имеет вещественный корень. Например, кубическое уравнение х 3 + ax 2 +bх+с = 0 всегда имеет хотя бы одно решение, так как левая часть при больших по модулю и отрицательных х меньше нуля (слагаемое х 3 «перевесит» все остальные), а при положительных больших х станет больше нуля.
Для разрывных функций сформулированное утверждение может оказаться неверным, как показывает простой пример функции 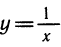
Уравнения, тождества, неравенства: определения и классификация
Уравнением называется равенство двух математических выражений с одной или несколькими переменными. В математике рассматриваются два вида равенств — тождества и уравнения. Тождество — это равенство, которое выполняется при всех допустимых значениях входящих в него букв. Для записи тождества наряду со знаком обычного равенства «=» также используется знак тождественного равенства 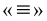
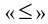
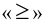
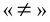
В общем виде уравнение с одним неизвестным имеет представление
где f(x) некоторая функция неизвестной x. Областью (множеством) допустимых значений (ОДЗ) неизвестной x в этом случае называют область определения функции f (х). Значения неизвестной x из области допустимых значений уравнения, обращающие уравнение в верное тождество, называют решениями (корнями) уравнения. Уравнение считается решённым, если найдены все его решения или показано, что оно не имеет решений. Аналогично всякое значение неизвестной x из области допустимых значений неравенства, обращающее неравенство в верное числовое неравенство, называется решением неравенства. Все решения неравенства образуют множество его решений.
Если у= f(x) — одна из основных элементарных функций, b — некоторое действительное число, то уравнение f(x) = b принято называть простейшим уравнением. Например, при 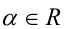
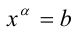
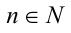
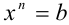
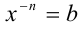
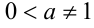
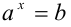
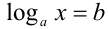
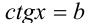
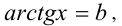
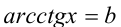
Пример:
Найти все значения а, при каждом из которых множество решений неравенства 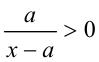
Решение:
Число x = 1 является решением неравенства тогда и только тогда, когда
Ответ:
Рассмотрим простейшую классификацию уравнений (неравенств), изучаемых в школьном курсе. В алгебраических уравнениях над неизвестными совершаются, и притом в конечном числе, лишь операции сложения, вычитания, умножения, деления, возведения в целую степень и извлечения корня. Если над неизвестными совершаются и другие операции, например возведение в иррациональную степень, взятие логарифма или синуса, или же перечисленные выше математические операции совершаются бесконечное число раз, то уравнение называется трансцендентным. В рациональных уравнениях отсутствует операция извлечения корня из выражения, содержащего неизвестные. В целых уравнениях отсутствует операция деления на выражение, содержащее неизвестные, а в дробных — такое деление есть.
Например: 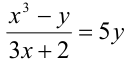
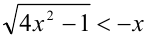
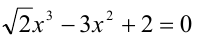
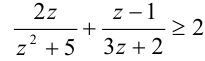
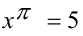
Любое целое рациональное алгебраическое уравнение с одним неизвестным x степени n после преобразований можно привести к стандартному виду:
где 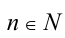
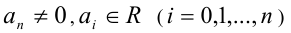
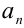
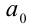
Пример:
Найти сумму коэффициентов многочлена, который получится после раскрытия скобок и приведения подобных членов в выражении:
Решение:
Конечно, никто не ожидает от вас на экзамене, что вы начнёте раскрывать скобки и приводить данный многочлен к стандартному виду. У этой задачи существует оригинальное и очень простое решение. Обозначим данный многочлен через f (х). Тогда искомая сумма его коэффициентов 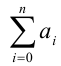
Ответ: сумма коэффициентов равна 1.
Пример:
Для каких значений параметра р отношение суммы коэффициентов многочлена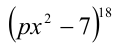
Решение:
Поскольку сумма коэффициентов данного многочлена равна его значению в точке x = 1, а его свободный член, как несложно увидеть, равен 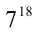
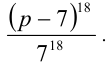
Пример:
Привести пример алгебраического уравнения с целыми коэффициентами, одним из корней которого является число
Решение:
Рассмотрим равенство 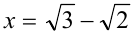
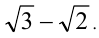
Уединим радикал 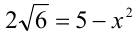
Благодаря операции возведения в квадрат удалось добиться того, чтобы все коэффициенты уравнения стали целочисленными. Полученное уравнение 4-й степени удовлетворяет условию задачи.
Замечание:
Эта задача имеет не единственный ответ. Любое алгебраическое следствие уравнения 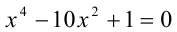
также можно было бы предъявить в качестве ответа.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
ГЛАВА VII
УРАВНЕНИЯ И НЕРАВЕНСТВА ПЕРВОЙ СТЕПЕНИ С ОДНИМ
НЕИЗВЕСТНЫМ
Видео:ЛИНЕЙНЫЕ НЕРАВЕНСТВА - Как решать линейные неравенства // Подготовка к ЕГЭ по МатематикеСкачать

Уравнения и неравенства первой степени с одним неизвестным
Два свойства уравнений
Мы много раз пользовались уравнениями и знаем, что они очень полезны для решения различных задач. Чтобы успешно, пользоваться уравнениями, надо хорошо знать их свойства и изучить различные приемы их решения..
Решение уравнений — один из основных вопросов курса алгебры. К этому вопросу мы будем возвращаться несколько раз. Сейчас рассмотрим два основных свойства уравнений.
Свойство:
Если к обеим частям уравнения прибавить
одно и то же число или один и то же многочлен относительно неизвестного, то полученное в результате этого новое уравнение имеет те же и только те же решения, что и исходное уравнение.
Или, другими словами: уравнение не теряет и не приобретает решения, когда к обеим частям его прибавляется одно и то же число или один и тот же многочлен относительно неизвестного.
Разъясним сначала, почему уравнение щ может потерять решение когда к обеим частям его прибавляется одно и то же число или один и тот же многочлен относительно неизвестного.
Это уравнение имеет решение x = 5. При х = 5 уравнение (1) превращается в тождество 6 = 6. Прибавим теперь к каждой части уравнения (1) по 20, получим новое уравнение
После замены в уравнении (2) буквы х числом 5 каждое из выражений, заключенных в скобки, дает в результате опять 6, и таким образом мы в каждой части получим 26. Разница между уравнением (1) и уравнением (2) заключается лишь в том, что при x = 5
уравнение (1) превращается в тождество 6 = 6, а уравнение (2) превращается в тождество 26 = 26.
Если бы к каждой части уравнения (1) прибавили не по 20, а по —200, новое уравнение опять при х=Ь превратилось бы в тождество. Различие между этим уравнением и уравнением (1) заключалось бы только в том, что в каждой части нового уравнения получилось бы по —194, а не по 6, как в уравнении (1).
Если бы мы к каждой части уравнения прибавили по многочлену 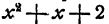
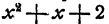
Выходит, что решение лг = б не теряете», когда к каждой части уравнения (1) прибавляется одно и то же число или один и тот же многочлен относительно неизвестного.
То, что мы показали на уравнении (1), можно также показать и на каком угодно другом уравнений. Так как вычитание любого числа и любого многочлена можно заменить сложением, уравнение не может потерять решение и тогда, когда от каждой части его отнимается одно и то же число или один и тот же многочлен относительно неизвестного.
Разъясним теперь, почему уравнение не может приобрести решение, когда к обеим частям его прибавляется одно и то же число или один и тот же многочлен относительно неизвестного. Рассмотрим
опять уравнение (1) и (2) и выясним, почему при переходе от уравнения (1) к уравнению (2) мы не могли приобрести решения.
Для того чтобы от уравнения (2) перейти к уравнению (1), достаточно от каждой части его отнять по 20 (или к каждой части прибавить по —20). Значит, при переходе от уравнения (2) к уравнению (1) мы не можем потерять решение.
Допустим теперь, что при переходе от уравнения (I) к
уравнению (2) мы приобрели какое-нибудь решение (скажем, x=2,5). Тогда при переходе от уравнения (2) назад к уравнению (1) мы должны потерять это решение, а это невозможно.
Замечание:
Так как буквы в алгебре обозначают числа, все сказанное об уравнениях с числовыми коэффициентами относится также и к уравнениям с буквенными коэффициентами.
Покажем, на примерах, как свойство 1 можно применять к решению уравнений.
Пример:
Решить уравнение х— 7 = 11.
Решение:
Прибавим к каждой части уравнения по 7, получим x = 18.
Пример:
Решить уравнение х + 30 = 10.
Решение:
Вычтем из каждой части уравнения по 30 (или прибавим по —30). Получим х = — 20
Пример:
Решить уравнение х — а=b.
Решение:
Прибавим к каждой части уравнения а, получим х = b+a
Следствие из свойства 1 уравнений. Любой член
уравнения можно перенести из одной части е другую, изменив при этом его знак на противоположный.
Это утверждение справедливо для любых уравнений. Чтобы упростить изложение, мы проведем его на частном примере.
Покажем, что —2х можно перенести с противоположным знаком в левую часть, т. е. покажем, что при переходе от уравнения (3) к уравнению
ни одно решение не теряется и не приобретается.
К каждой части уравнения (3) прибавим 2х, получим уравнение (4). На оснований свойства 1 уравнений переход от уравнения (3) к уравнению (4) происходит без потери и приобретения решений.
Все сказанное относительно —2х можно повторить относительно любого другого члена уравнение (3).
Этим свойством уравнений широка пользуются при решении уравнений. Именно, решая уравнения, часто переносят члены, содержащие неизвестные, в одну часть, а известные — в другую. Поясним это примером.
Пример:
Решение:
Перенесем неизвестные члены в левую часть, а известные в правую, получим
Свойство:
Если обе части уравнения умножить или
разделить на какое-нибудь число, отличное от нуля, то полученное в результате этого новое уравнение имеет те же и только те же решения, что и исходное уравнение.
Иными словами: уравнение не приобретает и не теряет решений от того, что обе части его умножены или разделены на одно и то же число, отличное от нуля.
Прежде чем разъяснить свойство 2, заметим, что его достаточно разъяснить для умножения, так как деление можно всегда заменить умножением на обратное число.
Мы и здесь, как и при разъяснении свойства 1, сначала расскажем, почему при умножении (или делении) обеих частей уравнения на одно и то же число, отличное от нуля, ни одно решение не может быть потеряно. После этого разъяснится и то, что ни одно решение не может быть при этом приобретено..
Возьмем какое-нибудь уравнение. Все, что будет показано на этом уравнении, можно показать и на любом другом уравнении.
имеет решение х = 6. Действительно, при x=Q уравнение
превращается в тождество 10 = 10.
Умножим каждую часть уравнения (5) на 20, получим уравнение
При х = 6 уравнение (6) тоже превращается в тождество
Если бы мы умножили обе части уравнения на 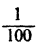
Выходит, что решение x=6 не теряется при умножении или делении каждой части уравнения (5) на одно и то же число.
От уравнения (6) можно, перейти обратно к уравнению (5) посредством умножения каждой части его
Ясно поэтому, что при переходе от уравнения (6) к уравнению (5) не может быть потери решения,
Отсюда вытекает, что при переходе от уравнения (5) к
уравнению (6) не могло быть и приобретения решения, Здесь опять, как и при изучении свойства 1, важно понять, что решения, приобретенные при переходе от уравнения (5) к уравнению (6), должны были бы
потеряться при обратном переходе, а потеря решения здесь невозможна.
Оно имеет единственное решение х = 6. Умножим каждую часть его на нуль. Получим
Уравнению (8) удовлетворяет не только х = б, но и любое другое значение х. (Например, положим х = 1 000, получим тождество 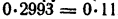
Выходит, что при переходе от уравнения (7) к уравнению (8) мы приобрели бесконечное множество решений. Вот почему в формулировке свойства 2 указано, что число, на которое умножаются обе части уравнения, должно быть отлично от нуля.
Замечание:
Так как буквы в алгебре обозначают числа, все сказанное об уравнениях с числовыми коэффициентами относится также и к уравнениям с буквенными коэффициентами. При этом необходимо только следить, за тем, чтобы при умножении обеих частей уравнения на буквенное выражение не вкралось умножение на нуль (Дело в том, что буквенные выражения могут при некоторых значениях входящих в них букв равняться нулю.)
Покажем на примерах, как свойство 2 можно применять к решению уравнений.
Пример:
Решить уравнение
Решение:
Разделим обе части уравнения на 2 получим
Пример:
Решить уравнение 15 — x = 20.
Решение:
Перенесем 15 в правую часть, получим
Умножим теперь обе части уравнения на —1,получим
Пример:
Решить уравнение ах=b.
Решение:
Если 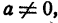
Если же а = 0, то уравнение имеет вид 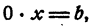
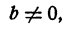
Пример:
Решить уравнение
Решение:
Здесь 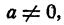
Понятие о равносильности уравнений
Определение:
Если каждое решение одного из уравнений является решением другого и каждое решение второго уравнения является решением первого, уравнения называются равносильными.
Пример:
имеет единственное решение x=11 Уравнение
имеет также единственное решение x=11 . Уравнение (1) и (2) равносильны.
Пример:
имеет два решения: 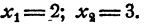
имеет также два решения: 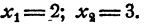
Пример:
не равносильны. Действительно, уравнение (5) имеет два решения: 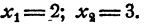
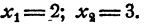
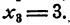
Теперь основные свойства уравнений можно сформулировать так:
Свойство:
Если к обеим частям уравнения прибавить
одно и то же число или один и тот же многочлен относительно неизвестного, то полученное в результате этого новое уравнение равносильно данному.
Свойство:
Если обе части уравнения умножить или
разделить на какое-нибудь число, отличное от нуля, то полученное в результате этого новое уравнение равносильно данному.
О некоторых преобразованиях уравнения, которые могут привести к потере или приобретению решений
При внимательном рассмотрении свойств 1 и 2 уравнений (§ 1) могут возникнуть два вопроса:
- В § 1 говорится о прибавлении к обеим частям уравнения многочленов относительно неизвестного. А что произойдет с решениями уравнения, если к обеим частям его прибавить не многочлен относительно неизвестного, а выражение, содержащее неизвестное в знаменателе?
- В § 1 говорится об умножении и делении обеих частей уравнения на любое число. А что произойдет с решением уравнения, если обе части его умножить или разделить на одно и то же выражение, содержащее неизвестное?
Мы сейчас приведем примеры, которые и помогут нам ответить на эти вопросы.
Пример:
имеет решение х = 8. Уравнение
полученное из уравнения (1) прибавлением к каждой части выражения 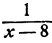
Теперь ясно, почему в § 1 шла речь о прибавлении многочленов от неизвестного.
Пример:
имеет единственное решение x= 3. Уравнение
полученное из уравнения (3) умножением обеих частей на х — 2, имеет два решения: 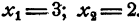
Теперь ясно, почему, в § 1 говорится об умножении и делении обеих частей уравнения на число, а не на выражения, которые содержат неизвестное.
Дело в том, что, умножая обе части уравнения на х — 2, мы умножаем их не на определенное число, а на выражение, которое при разных значениях х имеет разные значения и среди этих значений содержится нуль (при x = 2 выражение х — 2 равно нулю). Мы же знаем, что умножение обеих частей уравнения на нуль
приводит к приобретению решений (см. § 1).
При делении на х — 2 мы теряем решение потому, что в
выражении х — 2 скрыты разные значения и среди них содержится 0, на который делить нельзя.
Все сказанное здесь приводит к следующим выводам:
- Прибавление к обеим- частям уравнения выражения, содержащего неизвестное в знаменателе, может привести к потере и приобретению решений. При этом потерянными и
приобретенными решениями могут быть только те значения неизвестного, при которых знаменатель этого выражения равен нулю. - Умножение обеих частей уравнения на многочлен от неизвестного может привести к приобретению решений. При этом приобретенными решениями могут быть только те значения неизвестного, при которых этот многочлен равен нулю.
- Деление обеих частей уравнения на Решение уравнений
При решений уравнений можно поступать по следующему правилу:
- Освободить уравнение от дробей.
- Раскрыть скобки.
- Перенести все члены, содержащие неизвестные, в одну часть уравнения (в левую), а известные в другую.
- Сделать приведение подобных членов. В случае если неизвестное входит в несколько членов с буквенными коэффициентами, вынести неизвестное за скобки.
- Если в результате этих преобразований получится урaвнение видаax = b, то разделить обе части этого уравнения на коэффициент при неизвестном (а), не допуская деления на нуль.
Пример:
Решение:
Умножим обе части уравнения на 20 (20 — общее наименьшее кратное знаменателей)
Раскрыв скобки, имеем
Приведем подобные члены в каждой части уравнения
Перенесем 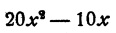
Пример:
Решение:
Чтобы освободить уравнение от дробей, умножим обе части его на (a + b) (а — b). Выражение (a + b) (а — b) отлично от нуля, так как иначе а+ b=0 или а — b= 0, и тогда уравнение (1) не имело бы смысла. Получим
Перенесем неизвестные в левую, а известные в правую часть
(Можно упростить решение, вычеркнув сразу после раскрытия скобок из каждой части уравнений одинаковые слагаемые ах и ab,) Приведем подобные члены
Теперь нам. следует делить oбе части уравнения на 2b. Это можно делать только в том случае, если 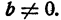
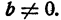
Если b=0, уравнение (1) принимает такой вид:
Это уравнение, очевидно, не имеет решения.
Ответ. Если 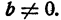
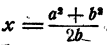
уравнение решений не имеет.
Пример:
Решение:
Умножим обе части уравнения на abc. Выражение abc отлично от нуля, так как иначе уравнение не имело бы смысла. Получим
Вынесем х за скобки, получим
Случай, когда ab+bc+ca = 0, представляет некоторые трудности для исследования, и потому мы оставим его без рассмотрения.
Ответ. Если 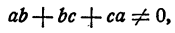
Видео:Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

О числе решений уравнения первой степени с одним неизвестным
Определение:
Уравнением первой степени с одним
неизвестным называется такое уравнение, которое после освобождения его от дробей, раскрытия скобок, перенесения всех членов в одну часть и приведения подобных членов принимает вид
где а и b — известные числа, а — называется коэффициентом при неизвестном, b — свободным членом.
Пример:
Уравнения, рассмотренные в § 4, — уравнения первой степени с одним неизвестным.
Уравнение первой степени с одним неизвестным либо имеет единственное решение, либо совсем не имеет решения, либо имеет бесконечное множество решений.
- Если коэффициент при неизвестном в уравнении первой степени с одним неизвестным отличен от нуля, уравнение имеет решение и притом единственное.
Пример. Уравнение З х + 2 = 0 имеет единственное решениеПример. Уравнение 2x=0 имеет единственное решение х=0.
- Если коэффициент при неизвестном в уравнении первой степени с одним неизвестным равен нулю, а свободный член неравен нулю, уравнение не имеет решения.
Пример. Уравнение0х + 1 = 0не имеет решения, так как при любом значении хпроизведение 0
х равно 0 и 0 + 1 =1.
- Если коэффициент при неизвестном и свободный член в уравнении первой степени с одним неизвестным равны нулю, уравнение имеет бесконечное множество решений. Всякое число
является решением такого уравнения. В самом деле, уравнению 0 • x +0 = 0 удовлетворяет любое
число, так как произведение любого числа и нуля равно нулю и 0 + 0 = 0.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Уравнения, содержащие неизвестное в знаменателе
К уравнениям первой степени с одним неизвестным приводятся и некоторые уравнения, содержащие неизвестное в знаменателе. Они решаются по тому же правилу, что и уравнения, не содержащие неизвестное в знаменателе.
Нужно только иметь в виду, что при освобождении такого уравнения от дробей приходится обе части его умножать на многочлен от неизвестного, и потому возможно приобретение решений или, как говорят, возможно появление посторонних решений.
Пример:
Решение:
Умножим обе части уравнения на 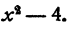
Получим
Так как при умножении на 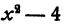
Проверка показала, что х = 8 есть решение уравнения. Таким образом, мы посторонних решений не ввели. Впрочем, это можно было установить и проще: при х = 8 выражение 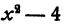
Пример:
Решение:
Умножим обе части уравнения на (x + 2)(x + 3).
Получим
При x = —2 уравнение не имеет смысла. Таким образом, х = —2 есть постороннее решение.
Ответ. Уравнение решений не имеет.
Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Решение задач при помощи уравнений. Понятие об исследовании задачи
Задачи, которые . приходится решать при помощи уравнений, весьма разнообразны и весьма разнообразны способы их решения. Поэтому нельзя дать общее правило, руководствуясь которым можно
было бы, не задумываясь, решить любую задачу при помощи уравнений. Часто бывает так, что способ, который с успехом применялся в решении одной задачи, непригоден для решения другой. Каждая задача требует для ее решения сообразительности,
изобретательности.
Научиться решать задачи можно только на практике. Чем больше мы будем решать задач, чем больше будем думать над их решением, чем больше будем стараться изобретать различные способы их решения, тем больше мы разовьем свою сообразительность, тем лучше будем решать задачи.
Мы сейчас для примера рассмотрим несколько задачки расскажем, как эти задачи решаются.
Рекомендуем внимательно рассмотреть эти решения и на них учиться самостоятельному решению задач.
Задача:
Определить расстояние между пунктами А и В, если велосипедист, делающий по 15 км в час, проезжал это расстояние на 2 мин. скорее, чем другой велосипедист, проезжающий по 12 км в час?
Решение:
Обозначим буквой х расстояние между А и В (в
километрах). Первый велосипедист проехал это расстояние в 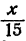
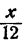
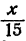
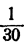
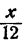
Уравнение составлено. Из него имеем
Проверка. Первый велосипедист 2 км проезжает в 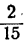
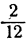
Замечание:
Рекомендуем обратить внимание на следующее:
- Буквойхв рассмотренной задаче мы обозначили искомую величину. Так можно поступать при решении многих задач. В дальнейшем, мы покажем, что иногда лучше поступать иначе и обозначать буквой л: другую величину, которая не является искомой.
- В рассмотренной задаче мы имели дело с двумя величинами, из которых одна на некоторое количество меньше другой
При составлении уравнения мы к меньшей из величин добавили соответствующее количество и полученную сумму приравняли большей. Вместо этого мы могли бы из большей величины вычесть соответствующее количество и полученную разность приравнять меньшей.
Задача:
Самолет летел сначала со скоростью 180 км в час. Когда ему осталось пролететь на 320 км меньше, чем он пролетел, он стал лететь со скоростью 250 км в час. Средняя скорость на всем пути оказалась равной 200 км в час. Сколько всего километров пролетел самолет?
Решение:
Обозначим буквой х расстояние (в километрах), которое самолет пролетел со скоростью 180 км в час. Тогда ему осталось после этого пролететь (х— 320) км. Всего самолет пролетел
Так как средняя скорость оказалась равной 200 км в час, самолет на весь путь потратил
На первую часть пути он потратил 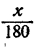
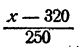
Мы получили два различных выражения для времени (в часах), которое самолет потратил на весь путь. Выходит, что
Уравнение составлено. Имеем
Умножим обе части уравнения на 4500, получим
Итак, первая, часть пути составляет 720 км, вторая 400 км (720 — 320 = 400 км), Значит, весь путь составляет 1120 км.
Проверка. На первую часть пути самолет потратил 4 часа 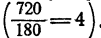
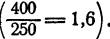
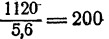
Замечание:
Рекомендуем обратить внимание на следующее: буквой х мы обозначили здесь не искомую величину (все расстояние, которое пролетел самолет), а другую величину (первую часть этого расстояния). Мы поступили так потому, что при таком обозначении проще составить уравнение и, кроме того, потому, что, зная первую часть расстояния, нетрудно найти и все расстояние.
Впрочем, можно обозначить буквой х и все расстояние в километрах. Тогда для определения первой и второй части расстояния надо х разделить на 2 части так, чтобы одна была на 320 больше другой. Делается это так: от х отнимается 320 и полученная разность делится на 2, получается 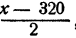
есть количество часов, потраченных на первую часть пути.
есть количество часов, потраченных на вторую часть пути.
есть количество часов, потраченных на весь путь, т. е
Решив это уравнение, получим х = 1120, т. е. тот же ответ, что и раньше. Из этого примера видно, что простота решения задачи зависит от того, насколько удачно выбрана величина, обозначаемая буквой х.
Задача:
Ученики собрали 3 кг 200 г семян белой акации,
желтой акации, клена и липы. Сколько семян каждого вида в отдельности собрали ученики, если семян белой акации они собрали в 3 раза больше, чем семян липы; семян клена собрано в 2 раза больше, чем семян белой акации и липы вместе, а семян желтой акации на 1 кг 200 г больше, чем семян клена?
Решение:
Мы должны определить четыре неизвестных величины: количество семян белой акации, желтой акации, клена и липы. При внимательном рассмотрении условия задачи видно, что, если бы мы узнали количество семян липы, нам нетрудно было бы узнать и остальные неизвестные величины.
Предположим, что семян липы собрано х г. Тогда семян белой акации собрано 3 х г. Семян клена собрано 2(x+3х) = 8х г. Семян желтой акации собрано (8х+1200)г,
Теперь нетрудно подсчитать, сколько собрано всех семян. Для этого достаточно сложить [х+Зх+8х(8х+1200)] г. Но, по условию, всех семян собрано 3200 г. Значит,
Теперь нетрудно написать и ответ: семян липы собрано 100 г, семян белой акации — 300 г, семян клена — 800 г, семян желтой акации — 2 кг. Проверка ответа не представляет труда.
На примере этой задачи видно, что посредством уравнений с одним неизвестным можно решать не только задачи с одной искомой величиной, но и такие задачи, в которых имеется несколько искомых величин.
Задача:
Периметр треугольника 44 см. Стороны треугольника относятся как 10:7:5. Определить стороны треугольника.
Решение:
Пусть меньшая сторона треугольника равна 5х см. Тогда средняя сторона этого треугольника равна 1х см, а бoльшая сторона равна 10x см. По условию,
Выходит, что меньшая сторона треугольника равна 10 см, средняя 14 см, а большая 20 см. Нетрудно проверить, что задача решена правильна
Ответ. 10 см;14 см; 20 см.
Замечание:
При решении последней задачи рекомендуем обратить внимание на следующее.
1) В задаче три искомые величины, но мы их выразили через одно неизвестное х.
2) Буквой х (в см) мы обозначили 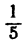
Конечно, можно было бы обозначить буквой х и всю меньшую сторону, но тогда средняя сторона была бы равна 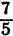
Задача:
В комнате № 1 общежития живут 9 человек, а в
комнате № 2 — 6 человек. Сколько человек надо переселить из комнаты № 1 в комнату № 2, чтобы в каждой комнате проживало по одному и тому же числу людей?
Решение:
Обозначим буквой х искомое количество людей. Тогда
Мы не напишем в ответе, что надо переселить 1,5 человека, так как это было бы бессмысленно. Мы должны сказать, что задача не имеет решения.
Ответ. Задача не имеет решения.
Задача:
Числитель дроби составляет 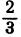
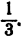
Решение:
Обозначим знаменатель дроби буквой х. Тогда числитель ее будет 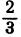
Ответ. Дроби, удовлетворяющей условию задачи, не существует.
Задача:
Сумма цифр двузначного числа равна 14. Если к этому числу прибавить 72,, то в результате получается число, записанное теми же цифрами, но в обратном порядке. Найти число.
Решение:
Обозначим Цифру десятков искомого числа буквой х. Тогда цифра единиц этого числа равна 14 — x. Имеем
Выходит, что цифра десятков искомого числа равна 3, а цифра единиц равна 11.
Ответ. Так как цифра не может быть больше 9,
задача решения не имеет.
Задача:
Одна машинистка может выполнить некоторую работу за 5 час. Во сколько часов может выполнить эту работу вторая машинистка, если, работая совместно, обе машинистки выполнили ту же работу в 6 час?
Решение:
Предположим, что вторая машинистка может
выполнить эту работу в х час. Тогда в 1 час она выполнит 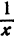
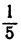
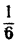
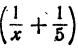
Ответ. Так как искомое чрсло часов не может быть отрицательно, задача решения не имеет.
Обратим .внимание на следующее. Уравнения, к которым приводили последние четыре задачи, имеют решения, а задачи все же не имеют решения, В первой из этих задач оказалось, что искомое число людей должно быть дробным; в-следующей задаче оказалось, что знаменатель дроби должен быть равен 0; в предпоследней задаче оказалось, что число единиц двузначного числа больше 9, в последней задаче
оказалось, что машинистка выполняет некоторую работу в отрицательное число часов.
Отсюда вытекает, что всякое решение требует еще и проверки его по смыслу. Мало того, крайне важно выяснить: почему данная задача не имеет решения, где в условии задачи кроются х причины, в силу которых задача не имеет решения, при каких численных данных подобная задача имеет решение.
Такая работа над задачей называется исследованием задачи.
Проведем, исследование рассмотренных четырех задач.
Исследование первой з а д а ч и. Дробное число людей,
которых надо переселить из одной комнаты в другую, возникло потому, что в одной комнате проживает чётное число людей, а в другой нечетное. Если бы числа проживающих в этих комнатах людей были одной четности, отрет был бы выражен целым числом. При этом, если в комнате № 1 живет больше людей, чем в комнате № 2, в ответе будет целое положительное число. Если в обеих комнатах живет по одинаковому числу людей, в ответе будет 0, и такой ответ означает,
что никого переселять из одной комнаты в другую не надо. Если, наконец, в комнате № 1 проживает меньше людей, чем в комнате № 2 в ответе получится целое отрицательное число, и такой ответ означает, что переселять надо не из комнаты № 1 в комнату № 2, а наоборот— из второй в первую»
Исследование второй задачи. Знаменатель дроби оказался равным нулю, потому что 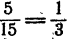
Исследование третьей задачи. Двузначных-чисел, сумма, цифр которых 14, существует всего пять: 59, 68, 77, 86 и 95. Если к любому из них прибавить 72, в результате получится не двузначное, а трехзначное число. Если в условии задачи заменить число 72
числом 36, задача будет иметь решение, так как 95 — 59 = 36, Точно так же задача будет иметь решение, если, в условии ее число 72 заменить числом 18, так как 86 — 68 = 18.
Исследование четвертой задачи. Отрицательный ответ
получился потому, что по условию две машинистки, работая совместно, тратят на- выполнение работы больше времени (6 час), чем одна машинистка (5 час). Так могло бы быть, если бы вторая машинистка
не помогала первой, а уничтожала бы работу, выполненную первой машинисткой. Для того чтобы задача имела решение, достаточно число 6 в условии заменить каким-нибудь положительным числом, меньшим 5, или число 5 заменить числом, большим 6. Можно, конечно, сразу заменить и оба числа, только при -этом нужно, чтобы вдвоем машинистки меньше тратили времени на работу, чем одна.
Задача:
На трех складах находится 300 куб. м дров. На первом складе 110 куб. м. На втором складе на несколько куб, метров больше, чем на первом, а на третьем складе на столько же куб. метров меньше, чем, на первом. Сколько куб. метров дров на каждом складе?
Решение:
Пусть на втором складе на х 
Уравнение не имеет решения.
Ответ. Задача не имеет решения.
Последняя задача не имеет решения, и этим она похожа на предыдущие четыре задачи. Однако здесь есть и различие. Это различие заключается в том, что предыдущие задачи приводили ю уравнениям, которые имели решения, но эти решения не подходили по смыслу. Последняя же задача привела к уравнению, которое не имеет решения.
Исследование задачи. Где в условии кроется причина того, что задача не имеет решения? По смыслу задачи на втором и на третьем складах вместе должно быть дров вдвое больше, чем на первом. Значит, на первом складе должно быть 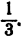
что либо надо 300 заменить на 330, либо надо 110 заменить на 100, либо заменить оба числа так, чтобы одно было в 3 раза больше другого. Заменим, например, 300 на 330, тогда получим уравнение
Этому уравнению удовлетворяет любое число. Выходит, что задача имеет бесконечное число решений. По смыслу задачи х может быть любым числом, абсолютная величина которого не превосходит 110.
Все сказанное по поводу решения задач при помощи уравнений приводит к следующему выводу.
Решение задачи при помощи уравнений состоит из четырех частей:
1) составления уравнения,
2) решения уравнения,
3) проверки,
4) исследования.
Наиболее трудная часть работы заключается в составлении уравнения. При составлений уравнения большое значение имеет удачный или неудачный выбор величины для обозначения ее буквой. Большое
внимание требуется и при исследовании решения.
Применение уравнений к решению задач в общем виде
Мы рассмотрели ряд задач с числовыми данными. Известно, однако, что особый интерес представляют задачи в общем виде, т. е. задачи с буквенными данными. Так как буквы обозначают у нас числа, решение задач с буквенными данными ведется так же, как и задач с числовыми данными, только всякий раз нужно исследовать решение. Покажем это на примере.
Задача:
Отцу 40 лет, сыну 10 лет. Через сколько лет отец будет в n раз старше сына?
Решение:
Предположим, что через х лет отец будет в n раз старше сына. Через х лет отцу будет (40 + x) лет, а сыну (10 +x ) лет. Значит,
Уравнение составлено. Решая его, имеем:
По смыслу задачи n > 1, поэтому знаменатель — всегда
положительное число. Что касается числителя, то при x 4 числитель отрицателен. Исследование показывает, что возможны три случая:
Случай 1. n 4. В этом случае задача имеет отрицательное решение, которое означает, что | x | лет назад отец был в n раз старше сына. Пусть, например, n = 6. Тогда x = —4; х = 4. Действительно, 4 года назад отцу было 36 лет, сыну 6 лет, и отец был в 6 раз старше сына.
Видео:Решение квадратных неравенств | МатематикаСкачать

Понятие о неравенстве
При исследовании уравнений с буквенными коэффициентами приходится решать такие задачи:
Даны два алгебраических выражения, зависящие от одной или нескольких букв. Требуется узнать, при каких значениях этих букв одно из данных выражений больше или меньше другого. Например, исследуя задачи из § 8, мы должны были узнать, при каких значениях n выражение 40—10n является положительным числом и при каких значениях n это выражение является отрицательным числом. Иными
словами, нам нужно было узнать, при каких значениях n
и при каких значениях n
В таких случаях говорят, что нам нужно было решить два неравенства: 40>10n и 40 или знаком
Выражение, записанное слева от знака неравенства, называется левой частью неравенства, а выражение, записанное справа от этого знака, называются правой частью неравенства.
При желании части неравенства можно переменить местами, но тогда надо изменить знак неравенства на. знак противоположного смысла, т. е. вместо знака ]> писать знак . Перепишем неравенства (1), переменив местами правую и левую части. Получим
Неравенства (1) и (2) не содержат букв, это так называемые числовые неравенства. Неравенства
Неравенства, не содержащие букв, могут быть верными
(справедливыми) или неверными (несправедливыми). Так, например, все неравенства (1) и (2) верные. Нетрудно указать и несправедливое неравенство. Для этого достаточно в верном неравенстве заменить знак
неравенства знаком противоположного смысла.
С неравенствами, содержащими буквы, дело обстоит сложнее. Рассмотрим для примера знакомое нам неравенство
Мы знаем, чтo это неравенство справедливо при n надо заменить знаком = , а при n > 4 знак > надо заменить знаком
Действительно, при любом а левая часть неравенства (5) на 1 больше правой.
С другой стороны, нетрудно указать и такое неравенство, которое при любых значениях входящих в него букв несправедливо. Для этого достаточно в неравенстве, которое справедливо при всех значениях входящих в него букв, заменить знак неравенства знаком противоположного смысла. Так, например, заменим в неравенстве (5) знак > знаком
которое при всех значениях буквы а несправедливо.
Определение:
Решить неравенство — это значит узнать, при каких значениях входящих в него букв это неравенство справедливо.
Пример:
Решить неравенство 40 > 10n.
Пример:
Решить неравенство 40 Свойства неравенств
Для того чтобы научиться решать неравенства, надо изучить их свойства.
Свойство:
Возьмем какое-нибудь справедливое неравенство, например
Прибавим к каждой части этого неравенства одно и то же число, например 10. Получим новое неравенство 5 + 10 > 3 + 10 или
Неравенство (2) тоже справедливо. В самом деле, мы к большему числу 5 и к меньшему числу 3 прибавили поровну (по 10), понятно, поэтому, что первая сумма больше второй.
Возьмем неравенство (1). Вычтем теперь из каждой части этого неравенства одно и то же число, например 10. Получим новое неравенство
Неравенство (3) тоже справедливо.
Возьмем еще раз неравенство (1). Прибавим к каждой его часта одно и то же буквенное выражение, например а + 2b. Получим новое неравенство
Неравенство (4) справедливо при любых значениях а и b. В самом деле, при каких угодно значениях а и b к правой и левой части неравенства (1) добавляется одно и то же число.
Пусть, например, а=3; b=4, тогда
и выходит, что при этих значениях а и b к каждой части неравенства (1) прибавлено по 11. Если а и b имеют какие-нибудь другие значения, все равно а + 2b, добавленное к левой части неравенства (1), имеет
то же значение, что и а + 2b, добавленное к правой части этого неравенства.
Теперь мы можем сформулировать свойство 1 неравенств:
Если а > b и с — произвольное число, то а + с > b + с;
а— с > b— с, т. е. к обеим частям неравенства можно прибавить или от обеих частей его вычесть одно и то же число или буквенное выражение.
Как легко видеть, свойство 1 неравенств очень напоминает соответствующее свойство равенств.
Следствие из свойства 1. Любой член неравенства можно перенести из одной части в другую, переменив при этом знак его на противоположный.
Действительно, рассмотрим неравенство
Нетрудно проверить, что это неравенство справедливо. Допустим, что мы хотим число —2 перенести из правой части в левую. Прибавим к каждой части неравенства по 2, получим опять справедливое неравенство
Сравнивая неравенство (6) с неравенством (5), видим, что неравенство (6) получается из неравенства (5) посредством переноса числа (—2) из правой части в левую, но с противоположным знаком.
Свойство:
Возьмем какое-нибудь справедливое неравенство, например
Умножим обе части этого неравенства на одно и то же положительное число, например на 5. Получим новое неравенство
Неравенство (2) тоже справедливо.
Возьмем опять то же неравенство
Разделим обе части этого неравенства на одно и то же
положительное число, например на 10. Получим новое неравенство
Неравенство (3) тоже справедливо.
Возьмем еще раз неравенство 3 >—2. Умножим обе части этого неравенства на какое-нибудь отрицательное число, например на —5. В левой части получится —15, а в правой 10. Ясно, что
Как видно, чтобы получить справедливое неравенство (4), нам пришлось знак > заменить знаком
Разделим обе части его на какое-нибудь отрицательное число, например на —10. В левой части получится —0,3, а в правой 0,2. Чтобы новое неравенство было справедливым, необходимо знак > заменить
знаком
Теперь мы можем сформулировать свойство 2 неравенств:
Если а > b и с положительно, то 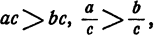
Если а>b и с отрицательно, то 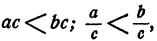
Если обе части неравенства умножить на нуль, неравенство превращается в равенство.
Пример:
Умножим обе части неравенства 3 > — 2 на нуль. В левой части получится 0, в правой части получится тоже 0, т. е.
Вместо знака > приходится писать знак=.
При умножении или делении обеих частей неравенства на буквенное выражение нужно быть весьма осторожным, так как при различных значениях букв это выражение может оказаться и положительным,
и отрицательным, и нулем. Так, например, неравенство 3 > — 2 при умножении на х дает
Решение неравенств первой степени с одним неизвестным
Определение:
Неравенством первой степени с одним
неизвестным называется такое неравенство, которое не содержит неизвестного в знаменателе и после освобождения его от дробей, раскрытия скобок, перенесения всех членов в левую часть и приведения
подобных членов имеет вид ах + b > 0 или ах + b
Решение:
Перенесем 2х в левую, а —1 в правую часть
неравенства. Получим
Этот ответ означает, что данное неравенство справедливо при любом значении х, большем чем —4. Ответ. x > —4.
Пример:
Решить неравенство 5х + 2
Разделим обе части неравенства на 3, получим
Ответ.
Пример:
Решить неравенство 2х + 5 > 7х — 10.
Решение:
Перенесем 2х в правую, а —10 в левую часть
неравенства. Получим
Разделим обе части неравенства на 5. Получим
Это неравенство можно решить и иначе. Например, перенесем 7х в левую, а 5 в правую часть. Получим
Разделим обе части неравенства на —5. Получим опять
Ответ. х
Решение:
Умножим обе части неравенства на 6. Получим
Перенесем —8х в правую часть. Получим
Ответ.
Пример:
Решить неравенство ах 0), то 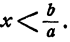
Решение:
Так как b и d одного знака, bd положительно.
Поэтому, умножив обе части справедливого по условию неравенства 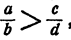
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Общие сведения о неравенствах
Данный материал может показаться сложным для понимания. Рекомендуется изучать его маленькими частями.
Определения и свойства
Неравенством мы будем называть два числовых или буквенных выражения, соединенных знаками >, 5 > 3
Данное неравенство говорит о том, что число 5 больше, чем число 3. Острый угол знака неравенства должен быть направлен в сторону меньшего числа. Это неравенство является верным, поскольку 5 больше, чем 3.
Если на левую чашу весов положить арбуз массой 5 кг, а на правую — арбуз массой 3 кг, то левая чаша перевесит правую, и экран весов покажет, что левая чаша тяжелее правой:
Если 5 > 3 , то 3 . То есть левую и правую часть неравенства можно поменять местами, изменив знак неравенства на противоположный. В ситуации с весами: большой арбуз можно положить на правую чашу, а маленький арбуз на левую. Тогда правая чаша перевесит левую, и экран покажет знак
Если в неравенстве 5 > 3 , не трогая левую и правую часть, поменять знак на , то получится неравенство 5 . Это неравенство не является верным, поскольку число 3 не может быть больше числа 5.
Числа, которые располагаются в левой и правой части неравенства, будем называть членами этого неравенства. Например, в неравенстве 5 > 3 членами являются числа 5 и 3.
Рассмотрим некоторые важные свойства для неравенства 5 > 3 .
В будущем эти свойства будут работать и для других неравенств.
Свойство 1.
Если к левой и правой части неравенства 5 > 3 прибавить или вычесть одно и то же число, то знак неравенства не изменится.
Например, прибавим к обеим частям неравенства число 4. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем вычесть из обеих частей неравенства 5 > 3 какое-нибудь число, скажем число 2
Видим, что левая часть по-прежнему больше правой.
Из данного свойства следует, что любой член неравенства можно перенести из одной части в другую часть, изменив знак этого члена. Знак неравенства при этом не изменится.
Например, перенесём в неравенстве 5 > 3 , член 5 из левой части в правую часть, изменив знак этого члена. После переноса члена 5 в правую часть, в левой части ничего не останется, поэтому запишем там 0
Видим, что левая часть по-прежнему больше правой.
Свойство 2.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь положительное число, скажем на число 2. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь число. Разделим их на 2
Видим, что левая часть по-прежнему больше правой.
Свойство 3.
Если обе части неравенства умножить или разделить на одно и то же отрицательное число , то знак неравенства изменится на противоположный.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь отрицательное число, скажем на число −2 . Тогда получим:
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь отрицательное число. Давайте разделим их на −1
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Само по себе неравенство можно понимать, как некоторое условие. Если условие выполняется, то неравенство является верным. И наоборот, если условие не выполняется, то неравенство не верно.
Например, чтобы ответить на вопрос является ли верным неравенство 7 > 3 , нужно проверить выполняется ли условие «больше ли 7, чем 3» . Мы знаем, что число 7 больше, чем число 3. То есть условие выполнено, а значит и неравенство 7 > 3 верно.
Неравенство 8 не является верным, поскольку не выполняется условие «8 меньше, чем 6».
Другим способом определения верности неравенства является составление разности из левой и правой части данного неравенства. Если разность положительна, то левая часть больше правой части. И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:
Число a больше числа b, если разность a − b положительна. Число a меньше числа b, если разность a − b отрицательна.
Например, мы выяснили, что неравенство 7 > 3 является верным, поскольку число 7 больше, чем число 3. Докажем это с помощью правила, приведённого выше.
Составим разность из членов 7 и 3. Тогда получим 7 − 3 = 4 . Согласно правилу, число 7 будет больше числа 3, если разность 7 − 3 окажется положительной. У нас она равна 4, то есть разность положительна. А значит число 7 больше числа 3.
Проверим с помощью разности верно ли неравенство 3 . Составим разность, получим 3 − 4 = −1 . Согласно правилу, число 3 будет меньше числа 4, если разность 3 − 4 окажется отрицательной. У нас она равна −1, то есть разность отрицательна. А значит число 3 меньше числа 4.
Проверим верно ли неравенство 5 > 8 . Составим разность, получим 5 − 8 = −3 . Согласно правилу, число 5 будет больше числа 8, если разность 5 − 8 окажется положительной. У нас разность равна −3, то есть она не является положительной. А значит число 5 не больше числа 8. Иными словами, неравенство 5 > 8 не является верным.
Строгие и нестрогие неравенства
Неравенства, содержащие знаки >, 5 > 3 , 7 .
Нестрогим, например, является неравенство 2 ≤ 5 . Данное неравенство читают следующим образом: «2 меньше или равно 5» .
Запись 2 ≤ 5 является неполной. Полная запись этого неравенства выглядит следующим образом:
Тогда становится очевидным, что неравенство 2 ≤ 5 состоит из двух условий: «два меньше пять» и «два равно пять» .
Нестрогое неравенство верно в том случае, если выполняется хотя бы одно из его условий. В нашем примере верным является условие «2 меньше 5» . Значит и само неравенство 2 ≤ 5 верно.
Пример 2. Неравенство 2 ≤ 2 является верным, поскольку выполняется одно из его условий, а именно 2 = 2.
Пример 3. Неравенство 5 ≤ 2 не является верным, поскольку не выполняется ни одно из его условий: ни 5 ни 5 = 2 .
Двойное неравенство
Число 3 больше, чем число 2 и меньше, чем число 4 . В виде неравенства это высказывание можно записать так: 2 . Такое неравенство называют двойным.
Двойное неравенство может содержать знаки нестрогих неравенств. К примеру, если число 5 больше или равно, чем число 2, и меньше или равно, чем число 7 , то можно записать, что 2 ≤ 5 ≤ 7
Чтобы правильно записать двойное неравенство, сначала записывают член находящийся в середине, затем член находящийся слева, затем член находящийся справа.
Например, запишем, что число 6 больше, чем число 4, и меньше, чем число 9.
Сначала записываем 6
Слева записываем, что это число больше, чем число 4
Справа записываем, что число 6 меньше, чем число 9
Неравенство с переменной
Неравенство, как и равенство может содержать переменную.
Например, неравенство x > 2 содержит переменную x . Обычно такое неравенство нужно решить, то есть выяснить при каких значениях x данное неравенство становится верным.
Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным.
Значение переменной, при котором неравенство становится верным, называется решением неравенства.
Неравенство x > 2 становится верным при x = 3, x = 4, x = 5, x = 6 и так далее до бесконечности. Видим, что это неравенство имеет не одно решение, а множество решений.
Другими словами, решением неравенства x > 2 является множество всех чисел, бóльших 2. При этих числах неравенство будет верным. Примеры:
Число 2, располагающееся в правой части неравенства x > 2 , будем называть границей данного неравенства. В зависимости от знака неравенства, граница может принадлежать множеству решений неравенства либо не принадлежать ему.
В нашем примере граница неравенства не принадлежит множеству решений, поскольку при подстановке числа 2 в неравенство x > 2 получается не верное неравенство 2 > 2 . Число 2 не может быть больше самого себя, поскольку оно равно самому себе (2 = 2) .
Неравенство x > 2 является строгим. Его можно прочитать так: « x строго больше 2″ . То есть все значения, принимаемые переменной x должны быть строго больше 2. В противном случае, неравенство верным не будет.
Если бы нам было дано нестрогое неравенство x ≥ 2 , то решениями данного неравенства были бы все числа, которые больше 2, в том числе и само число 2. В этом неравенстве граница 2 принадлежит множеству решений неравенства, поскольку при подстановке числа 2 в неравенство x ≥ 2 получается верное неравенство 2 ≥ 2 . Ранее было сказано, что нестрогое неравенство является верным, если выполняется хотя бы одно из его условий. В неравенстве 2 ≥ 2 выполняется условие 2 = 2 , поэтому и само неравенство 2 ≥ 2 верно.
Как решать неравенства
Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств мы будем применять свойства, которые изучили вначале данного урока, такие как: перенос слагаемых из одной части неравенства в другую часть, меняя знак; умножение (или деление) обеих частей неравенства на одно и то же число.
Эти свойства позволяют получить неравенство, которое равносильно исходному. Равносильными называют неравенства, решения которых совпадают.
Решая уравнения мы выполняли тождественные преобразования до тех пор, пока в левой части уравнения не оставалась переменная, а в правой части значение этой переменной (например: x = 2, x = 5 ). Иными словами, заменяли исходное уравнение на равносильное ему уравнение до тех пор, пока не получалось уравнение вида x = a , где a значение переменной x . В зависимости от уравнения, корней могло быть один, два, бесконечное множество, либо не быть совсем.
А при решении неравенств мы будем заменять исходное неравенство на равносильное ему неравенство до тех пор, пока в левой части не останется переменная этого неравенства, а в правой части его граница.
Пример 1. Решить неравенство 2x > 6
Итак, нужно найти такие значения x , при подстановке которых в 2x > 6 получится верное неравенство.
Вначале данного урока было сказано, что если обе части неравенства разделить на какое-нибудь положительное число, то знак неравенства не изменится. Если применить это свойство к неравенству, содержащему переменную, то получится неравенство равносильное исходному.
В нашем случае, если мы разделим обе части неравенства 2x > 6 на какое-нибудь положительное число, то получится неравенство, которое равносильно исходному неравенству 2x > 6.
Итак, разделим обе части неравенства на 2.
В левой части осталась переменная x , а правая часть стала равна 3. Получилось равносильное неравенство x > 3. На этом решение завершается, поскольку в левой части осталась переменная, а в правой части граница неравенства.
Теперь можно сделать вывод, что решениями неравенства x > 3 являются все числа, которые больше 3. Это числа 4, 5, 6, 7 и так далее до бесконечности. При этих значениях неравенство x > 3 будет верным.
Отметим, что неравенство x > 3 является строгим. « Переменная x строго больше трёх».
А поскольку неравенство x > 3 равносильно исходному неравенству 2x > 6 , то их решения будут совпадать. Иначе говоря, значения, которые подходят неравенству x > 3, будут подходить и неравенству 2x > 6. Покажем это.
Возьмём, например, число 5 и подставим его сначала в полученное нами равносильное неравенство x > 3 , а потом в исходное 2x > 6 .
Видим, что в обоих случаях получается верное неравенство.
После того, как неравенство решено, ответ нужно записать в виде так называемого числового промежутка следующим образом:
В этом выражении говорится, что значения, принимаемые переменной x , принадлежат числовому промежутку от трёх до плюс бесконечности.
Иначе говоря, все числа, начиная от трёх до плюс бесконечности являются решениями неравенства x > 3 . Знак ∞ в математике означает бесконечность.
Учитывая, что понятие числового промежутка очень важно, остановимся на нём подробнее.
Числовые промежутки
Числовым промежутком называют множество чисел на координатной прямой, которое может быть описано с помощью неравенства.
Допустим, мы хотим изобразить на координатной прямой множество чисел от 2 до 8. Для этого сначала на координатной прямой отмечаем точки с координатами 2 и 8, а затем выделяем штрихами ту область, которая располагается между координатами 2 и 8. Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Числа 2 и 8 назовём границами числового промежутка. Рисуя числовой промежуток, точки для его границ изображают не в виде точек как таковых, а в виде кружков, которые можно разглядеть.
Границы могут принадлежать числовому промежутку либо не принадлежать ему.
Если границы не принадлежат числовому промежутку, то они изображаются на координатной прямой в виде пустых кружков.
Если границы принадлежат числовому промежутку, то кружки необходимо закрасить.
На нашем рисунке кружки были оставлены пустыми. Это означало, что границы 2 и 8 не принадлежат числовому промежутку. Значит в наш числовой промежуток будут входить все числа от 2 до 8, кроме чисел 2 и 8.
Если мы хотим включить границы 2 и 8 в числовой промежуток, то кружки необходимо закрасить:
В данном случае в числовой промежуток будут входить все числа от 2 до 8, включая числа 2 и 8.
На письме числовой промежуток обозначается указанием его границ с помощью круглых или квадратных скобок.
Если границы не принадлежат числовому промежутку, то границы обрамляются круглыми скобками.
Если границы принадлежат числовому промежутку, то границы обрамляются квадратными скобками.
На рисунке представлено два числовых промежутка от 2 до 8 с соответствующими обозначениями:
На первом рисунке числовой промежуток обозначен с помощью круглых скобок, поскольку границы 2 и 8 не принадлежат этому числовому промежутку.
На втором рисунке числовой промежуток обозначен с помощью квадратных скобок, поскольку границы 2 и 8 принадлежат этому числовому промежутку.
С помощью числовых промежутков можно записывать ответы к неравенствам. Например, ответ к двойному неравенству 2 ≤ x ≤ 8 записывается так:
То есть сначала записывают переменную, входящую в неравенство, затем с помощью знака принадлежности ∈ указывают к какому числовому промежутку принадлежат значения этой переменной. В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
Обратим внимание на то, что ответ записан с помощью квадратных скобок, поскольку границы неравенства 2 ≤ x ≤ 8 , а именно числа 2 и 8 принадлежат множеству решений этого неравенства.
Множество решений неравенства 2 ≤ x ≤ 8 также можно изобразить с помощью координатной прямой:
Здесь границы числового промежутка 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8 , а выделенная штрихами область соответствует множеству значений x , которые являются решениями неравенства 2 ≤ x ≤ 8 .
В некоторых источниках границы, которые не принадлежат числовому промежутку, называют открытыми.
Открытыми их называют по той причине, что числовой промежуток остаётся открытым из-за того, что его границы не принадлежат этому числовому промежутку. Пустой кружок на координатной прямой математики называют выколотой точкой . Выколоть точку значит исключить её из числового промежутка или из множества решений неравенства.
А в случае, когда границы принадлежат числовому промежутку, их называют закрытыми (или замкнутыми), поскольку такие границы закрывают (замыкают) собой числовой промежуток. Закрашенный кружок на координатной прямой также говорит о закрытости границ.
Существуют разновидности числовых промежутков. Рассмотрим каждый из них.
Числовой луч
Числовым лучом называют числовой промежуток, который задаётся неравенством x ≥ a , где a — граница данного неравенства, x — решение неравенства.
Пусть a = 3 . Тогда неравенство x ≥ a примет вид x ≥ 3 . Решениями данного неравенства являются все числа, которые больше 3, включая само число 3.
Изобразим числовой луч, заданный неравенством x ≥ 3, на координатной прямой. Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Здесь точка 3 соответствует границе неравенства x ≥ 3 , а выделенная штрихами область соответствует множеству значений x , которые являются решениями неравенства x ≥ 3 .
Точка 3, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≥ 3 принадлежит множеству его решений.
На письме числовой луч, заданный неравенством x ≥ a, обозначается следующим образом:
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница числового луча принадлежит ему, а другая нет, поскольку бесконечность сама по себе границ не имеет и подразумевается, что по ту сторону нет числа, замыкающего этот числовой луч.
Учитывая то, что одна из границ числового луча закрыта, данный промежуток часто называют закрытым числовым лучом.
Запишем ответ к неравенству x ≥ 3 с помощью обозначения числового луча. У нас переменная a равна 3
В этом выражении говорится, что переменная x , входящая в неравенство x ≥ 3, принимает все значения от 3 до плюс бесконечности.
Иначе говоря, все числа от 3 до плюс бесконечности, являются решениями неравенства x ≥ 3 . Граница 3 принадлежит множеству решений, поскольку неравенство x ≥ 3 является нестрогим.
Закрытым числовым лучом также называют числовой промежуток, который задаётся неравенством x ≤ a . Решениями неравенства x ≤ a являются все числа, которые меньше a , включая само число a .
К примеру, если a = 2 , то неравенство примет вид x ≤ 2 . На координатной прямой граница 2 будет изображаться закрашенным кружком, а вся область, находящаяся слева, будет выделена штрихами. В этот раз выделяется левая часть, поскольку решениями неравенства x ≤ 2 являются числа, меньшие 2. А меньшие числа на координатной прямой располагаются левее
Здесь точка 2 соответствует границе неравенства x ≤ 2 , а выделенная штрихами область соответствует множеству значений x , которые являются решениями неравенства x ≤ 2 .
Точка 2, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≤ 2 принадлежит множеству его решений.
Запишем ответ к неравенству x ≤ 2 с помощью обозначения числового луча:
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x ≤ 2. Граница 2 принадлежит множеству решений, поскольку неравенство x ≤ 2 является нестрогим.
Открытый числовой луч
Открытым числовым лучом называют числовой промежуток, который задаётся неравенством x > a , где a — граница данного неравенства, x — решение неравенства.
Открытый числовой луч во многом похож на закрытый числовой луч. Различие в том, что граница a не принадлежит промежутку, как и граница неравенства x > a не принадлежит множеству его решений.
Пусть a = 3 . Тогда неравенство примет вид x > 3 . Решениями данного неравенства являются все числа, которые больше 3, за исключением числа 3
На координатной прямой граница открытого числового луча, заданного неравенством x > 3, будет изображаться в виде пустого кружка. Вся область, находящаяся справа, будет выделена штрихами:
Здесь точка 3 соответствует границе неравенства x > 3 , а выделенная штрихами область соответствует множеству значений x , которые являются решениями неравенства x > 3 . Точка 3, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x > 3 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x > a , обозначается следующим образом:
Круглые скобки указывают на то, что границы открытого числового луча не принадлежат ему.
Запишем ответ к неравенству x > 3 с помощью обозначения открытого числового луча:
В этом выражении говорится, что все числа от 3 до плюс бесконечности, являются решениями неравенства x > 3 . Граница 3 не принадлежит множеству решений, поскольку неравенство x > 3 является строгим.
Открытым числовым лучом также называют числовой промежуток, который задаётся неравенством x , где a — граница данного неравенства, x — решение неравенства. Решениями неравенства x являются все числа, которые меньше a , исключая число a .
К примеру, если a = 2 , то неравенство примет вид x . На координатной прямой граница 2 будет изображаться пустым кружком, а вся область, находящаяся слева, будет выделена штрихами:
Здесь точка 2 соответствует границе неравенства x , а выделенная штрихами область соответствует множеству значений x , которые являются решениями неравенства x . Точка 2, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x , обозначается следующим образом:
Запишем ответ к неравенству x с помощью обозначения открытого числового луча:
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x Граница 2 не принадлежит множеству решений, поскольку неравенство x является строгим.
Отрезок
Отрезком называют числовой промежуток, который задаётся двойным неравенством a ≤ x ≤ b , где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2 , b = 8 . Тогда неравенство a ≤ x ≤ b примет вид 2 ≤ x ≤ 8 . Решениями неравенства 2 ≤ x ≤ 8 являются все числа, которые больше 2 и меньше 8. При этом границы неравенства 2 и 8 принадлежат множеству его решений, поскольку неравенство 2 ≤ x ≤ 8 является нестрогим.
Изобразим отрезок, заданный двойным неравенством 2 ≤ x ≤ 8 на координатной прямой. Для этого отметим на ней точки с координатами 2 и 8, а располагающуюся между ними область выделим штрихами:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8 , а выделенная штрихами область соответствует множеству значений x , которые являются решениями неравенства 2 ≤ x ≤ 8 . Точки 2 и 8, являющиеся границами отрезка, изображены в виде закрашенных кружков, поскольку границы неравенства 2 ≤ x ≤ 8 принадлежат множеству его решений.
На письме отрезок, заданный неравенством a ≤ x ≤ b обозначается следующим образом:
Квадратные скобки с обеих сторон указывают на то, что границы отрезка принадлежат ему. Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:
В этом выражении говорится, что все числа от 2 до 8 включительно, являются решениями неравенства 2 ≤ x ≤ 8 .
Интервал
Интервалом называют числовой промежуток, который задаётся двойным неравенством a , где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8 . Тогда неравенство a примет вид 2 . Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая числа 2 и 8.
Изобразим интервал на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 , а выделенная штрихами область соответствует множеству значений x , которые являются решениями неравенства 2 . Точки 2 и 8, являющиеся границами интервала, изображены в виде пустых кружков, поскольку границы неравенства 2 не принадлежат множеству его решений.
На письме интервал, заданный неравенством a обозначается следующим образом:
Круглые скобки с обеих сторон указывают на то, что границы интервала не принадлежат ему. Запишем ответ к неравенству 2 с помощью этого обозначения:
В этом выражении говорится, что все числа от 2 до 8, исключая числа 2 и 8, являются решениями неравенства 2 .
Полуинтервал
Полуинтервалом называют числовой промежуток, который задаётся неравенством a ≤ x , где a и b — границы данного неравенства, x — решение неравенства.
Полуинтервалом также называют числовой промежуток, который задаётся неравенством a .
Одна из границ полуинтервала принадлежит ему. Отсюда и название этого числового промежутка.
В ситуации с полуинтервалом a ≤ x ему (полуинтервалу) принадлежит левая граница.
А в ситуации с полуинтервалом a ему принадлежит правая граница.
Пусть a = 2 , b = 8 . Тогда неравенство a ≤ x примет вид 2 ≤ x . Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, включая число 2, но исключая число 8.
Изобразим полуинтервал 2 ≤ x на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x , а выделенная штрихами область соответствует множеству значений x , которые являются решениями неравенства 2 ≤ x .
Точка 2, являющаяся левой границей полуинтервала, изображена в виде закрашенного кружка, поскольку левая граница неравенства 2 ≤ x принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде пустого кружка, поскольку правая граница неравенства 2 ≤ x не принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a ≤ x обозначается следующим образом:
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница полуинтервала принадлежит ему, а другая нет. Запишем ответ к неравенству 2 ≤ x с помощью этого обозначения:
В этом выражении говорится, что все числа от 2 до 8, включая число 2, но исключая число 8, являются решениями неравенства 2 ≤ x .
Аналогично на координатной прямой можно изобразить полуинтервал, заданный неравенством a . Пусть a = 2 , b = 8 . Тогда неравенство a примет вид 2 . Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая число 2, но включая число 8.
Изобразим полуинтервал 2 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 , а выделенная штрихами область соответствует множеству значений x , которые являются решениями неравенства 2 .
Точка 2, являющаяся левой границей полуинтервала, изображена в виде пустого кружка, поскольку левая граница неравенства 2 не принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде закрашенного кружка, поскольку правая граница неравенства 2 принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a обозначается так: ( a ; b ] . Запишем ответ к неравенству 2 с помощью этого обозначения:
В этом выражении говорится, что все числа от 2 до 8, исключая число 2, но включая число 8, являются решениями неравенства 2 .
Изображение числовых промежутков на координатной прямой
Числовой промежуток может быть задан с помощью неравенства или с помощью обозначения (круглых или квадратных скобок). В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.
Пример 1. Изобразить числовой промежуток, заданный неравенством x > 5
Вспоминаем, что неравенством вида x > a задаётся открытый числовой луч. В данном случае переменная a равна 5. Неравенство x > 5 строгое, поэтому граница 5 будет изображаться в виде пустого кружкá. Нас интересуют все значения x, которые больше 5, поэтому вся область справа будет выделена штрихами:
Пример 2. Изобразить числовой промежуток (5; +∞) на координатной прямой
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью неравенства, а с помощью обозначения числового промежутка.
Граница 5 обрамлена круглой скобкой, значит она не принадлежит промежутку. Соответственно, кружок остаётся пустым.
Символ +∞ указывает, что нас интересуют все числа, которые больше 5. Соответственно, вся область справа от границы 5 выделяется штрихами:
Пример 3. Изобразить числовой промежуток (−5; 1) на координатной прямой.
Круглыми скобками с обеих сторон обозначаются интервалы. Границы интервала не принадлежат ему, поэтому границы −5 и 1 будут изображаться на координатной прямой в виде пустых кружков. Вся область между ними будет выделена штрихами:
Пример 4. Изобразить числовой промежуток, заданный неравенством −5
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью обозначения промежутка, а с помощью двойного неравенства.
Неравенством вида a , задаётся интервал. В данном случае переменная a равна −5 , а переменная b равна единице. Неравенство −5 строгое, поэтому границы −5 и 1 будут изображаться в виде пустых кружка. Нас интересуют все значения x, которые больше −5 , но меньше единицы, поэтому вся область между точками −5 и 1 будет выделена штрихами:
Пример 5. Изобразить на координатной прямой числовые промежутки [−1; 2) и [2; 5]
В этот раз изобразим на координатной прямой сразу два промежутка. Промежуток [−1; 2) является полуинтервалом, промежуток [2; 5] — отрезком.
У полуинтервала [−1; 2) левая граница принадлежит ему, а правая нет.
А у отрезка [2; 5] обе границы принадлежат ему.
Чтобы хорошо увидеть промежутки [−1; 2) и [2; 5] , первый можно изобразить на верхней области, а второй на нижней. Так и поступим:
Граница 2 закрашена потому что она входит в промежуток [2; 5] .
Пример 6. Изобразить на координатной прямой числовые промежутки [-1; 2) и (2; 5]
Квадратной скобкой с одной стороны и круглой с другой обозначаются полуинтервалы. Одна из границ полуинтервала принадлежат ему, а другая нет.
В случае с полуинтервалом [-1; 2) левая граница будет принадлежать ему, а правая нет. Значит левая граница будет изображаться в виде закрашенного кружка. Правая же граница будет изображаться в виде пустого кружка.
А в случае с полуинтервалом (2; 5] ему будет принадлежать только правая граница, а левая нет. Значит левая граница будет изображаться в виде пустого кружка. Правая же граница будет изображаться в виде закрашенного кружка.
Изобразим промежуток [-1; 2) на верхней области координатной прямой, а промежуток (2; 5] — на нижней:
Примеры решения неравенств
Неравенство, которое путём тождественных преобразований можно привести к виду ax > b (или к виду ax ), будем называть линейным неравенством с одной переменной.
В линейном неравенстве ax > b , x — это переменная, значения которой нужно найти, а — коэффициент этой переменной, b — граница неравенства, которая в зависимости от знака неравенства может принадлежать множеству его решений либо не принадлежать ему.
Например, неравенство 2x > 4 является неравенством вида ax > b . В нём роль переменной a играет число 2, роль переменной b (границы неравенства) играет число 4.
Неравенство 2x > 4 можно сделать ещё проще. Если мы разделим обе его части на 2, то получим неравенство x > 2
Получившееся неравенство x > 2 также является неравенством вида ax > b , то есть линейным неравенством с одной переменной. В этом неравенстве роль переменной a играет единица. Ранее мы говорили, что коэффициент 1 не записывают. Роль переменной b играет число 2.
Отталкиваясь от этих сведений, попробуем решить несколько простых неравенств. В ходе решения мы будем выполнять элементарные тождественные преобразования с целью получить неравенство вида ax > b
Пример 1. Решить неравенство x − 7
Прибавим к обеим частям неравенства число 7
В левой части останется x , а правая часть станет равна 7
Путём элементарных преобразований мы привели неравенство x − 7 к равносильному неравенству x . Решениями неравенства x являются все числа, которые меньше 7. Граница 7 не принадлежит множеству решений, поскольку неравенство строгое.
Когда неравенство приведено к виду x (или x > a ), его можно считать уже решённым. Наше неравенство x − 7 тоже приведено к такому виду, а именно к виду x . Но в большинстве школ требуют, чтобы ответ был записан с помощью числового промежутка и проиллюстрирован на координатной прямой.
Запишем ответ с помощью числового промежутка. В данном случае ответом будет открытый числовой луч (вспоминаем, что числовой луч задаётся неравенством x и обозначается как ( −∞ ; a)
На координатной прямой граница 7 будет изображаться в виде пустого кружка, а вся область, находящаяся слева от границы, будет выделена штрихами:
Для проверки возьмём любое число из промежутка ( −∞ ; 7 ) и подставим его в неравенство x вместо переменной x . Возьмём, например, число 2
Получилось верное числовое неравенство, значит и решение верное. Возьмём ещё какое-нибудь число, например, число 4
Получилось верное числовое неравенство. Значит решение верное.
А поскольку неравенство x равносильно исходному неравенству x − 7 , то решения неравенства x будут совпадать с решениями неравенства x − 7 . Подставим те же тестовые значения 2 и 4 в неравенство x − 7
Пример 2. Решить неравенство −4x
Разделим обе части неравенства на −4. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Мы привели неравенство −4x к равносильному неравенству x > 4 . Решениями неравенства x > 4 будут все числа, которые больше 4. Граница 4 не принадлежит множеству решений, поскольку неравенство строгое.
Изобразим множество решений неравенства x > 4 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 3. Решить неравенство 3y + 1 > 1 + 6y
Перенесём 6y из правой части в левую часть, изменив знак. А 1 из левой части перенесем в правую часть, опять же изменив знак:
Приведём подобные слагаемые:
Разделим обе части на −3. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства y являются все числа, меньшие нуля. Изобразим множество решений неравенства y на координатной прямой и запишем ответ в виде числового промежутка:
Пример 4. Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)
Раскроем скобки в обеих частях неравенства:
Перенесем −3x из правой части в левую часть, изменив знак. Члены −5 и 7 из левой части перенесем в правую часть, опять же изменив знаки:
Приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 8
Решениями неравенства 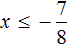
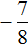
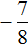
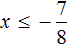
Изобразим множество решений неравенства 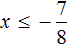
Пример 5. Решить неравенство
Умножим обе части неравенства на 2. Это позволит избавиться от дроби в левой части:
Теперь перенесем 5 из левой части в правую часть, изменив знак:
После приведения подобных слагаемых, получим неравенство 6x > 1 . Разделим обе части этого неравенства на 6. Тогда получим:
Решениями неравенства 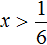
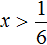
Изобразим множество решений неравенства 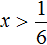
Пример 6. Решить неравенство
Умножим обе части на 6
После приведения подобных слагаемых, получим неравенство 5x . Разделим обе части этого неравенства на 5
Решениями неравенства x являются все числа, которые меньше 6. Граница 6 не принадлежит множеству решений, поскольку неравенство является x строгим.
Изобразим множество решений неравенства x на координатной прямой и запишем ответ в виде числового промежутка:
Пример 7. Решить неравенство
Умножим обе части неравенства на 10
В получившемся неравенстве раскроем скобки в левой части:
Перенесем члены без x в правую часть
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 10
Решениями неравенства x ≤ 3,5 являются все числа, которые меньше 3,5. Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.
Изобразим множество решений неравенства x ≤ 3,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 8. Решить неравенство 4
Чтобы решить такое неравенство, нужно переменную x освободить от коэффициента 4. Тогда мы сможем сказать в каком промежутке находится решение данного неравенства.
Чтобы освободить переменную x от коэффициента, можно разделить член 4x на 4. Но правило в неравенствах таково, что если мы делим член неравенства на какое-нибудь число, то тоже самое надо сделать и с остальными членами, входящими в данное неравенство. В нашем случае на 4 нужно разделить все три члена неравенства 4
Решениями неравенства 1 являются все числа, которые больше 1 и меньше 5. Границы 1 и 5 не принадлежат множеству решений, поскольку неравенство 1 является строгим.
Изобразим множество решений неравенства 1 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 9. Решить неравенство −1 ≤ −2x ≤ 0
Разделим все члены неравенства на −2
Получили неравенство 0,5 ≥ x ≥ 0 . Двойное неравенство желательно записывать так, чтобы меньший член располагался слева, а больший справа. Поэтому перепишем наше неравенство следующим образом:
Решениями неравенства 0 ≤ x ≤ 0,5 являются все числа, которые больше 0 и меньше 0,5. Границы 0 и 0,5 принадлежат множеству решений, поскольку неравенство 0 ≤ x ≤ 0,5 является нестрогим.
Изобразим множество решений неравенства 0 ≤ x ≤ 0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 10. Решить неравенство
Умножим обе неравенства на 12
Раскроем скобки в получившемся неравенстве и приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 2
Решениями неравенства x ≤ −0,5 являются все числа, которые меньше −0,5. Граница −0,5 принадлежит множеству решений, поскольку неравенство x ≤ −0,5 является нестрогим.
Изобразим множество решений неравенства x ≤ −0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 11. Решить неравенство
Умножим все части неравенства на 3
Теперь из каждой части получившегося неравенства вычтем 6
Каждую часть получившегося неравенства разделим на −1. Не забываем, что при делении всех частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства 3 ≤ a ≤ 9 являются все числа, которые больше 3 и меньше 9. Границы 3 и 9 принадлежат множеству решений, поскольку неравенство 3 ≤ a ≤ 9 является нестрогим.
Изобразим множество решений неравенства 3 ≤ a ≤ 9 на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Существуют неравенства, которые не имеют решений. Таковым, например, является неравенство 6x > 2(3x + 1) . В процессе решения этого неравенства мы придём к тому, что знак неравенства > не оправдает своего местоположения. Давайте посмотрим, как это выглядит.
Раскроем скобки в правой части данного неравенство, получим 6x > 6x + 2 . Перенесем 6x из правой части в левую часть, изменив знак, получим 6x − 6x > 2 . Приводим подобные слагаемые и получаем неравенство 0 > 2 , которое не является верным.
Для наилучшего понимания, перепишем приведение подобных слагаемых в левой части следующим образом:
Получили неравенство 0x > 2 . В левой части располагается произведение, которое будет равно нулю при любом x . А ноль не может быть больше, чем число 2. Значит неравенство 0x > 2 не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x > 2 , то не имеет решений и исходное неравенство 6x > 2(3x + 1) .
Пример 2. Решить неравенство
Умножим обе части неравенства на 3
В получившемся неравенстве перенесем член 12x из правой части в левую часть, изменив знак. Затем приведём подобные слагаемые:
Правая часть получившегося неравенства при любом x будет равна нулю. А ноль не меньше, чем −8. Значит неравенство 0x не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x , то не имеет решений и исходное неравенство 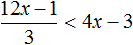
Ответ: решений нет.
Когда решений бесконечно много
Существуют неравенства, имеющие бесчисленное множество решений. Такие неравенства становятся верными при любом x .
Пример 1. Решить неравенство 5(3x − 9)
Раскроем скобки в правой части неравенства:
Перенесём 15x из правой части в левую часть, изменив знак:
Приведем подобные слагаемые в левой части:
Получили неравенство 0x . В левой части располагается произведение, которое будет равно нулю при любом x . А ноль меньше, чем 45. Значит решением неравенства 0x является любое число.
А если приведённое равносильное неравенство 0x имеет бесчисленное множество решений, то и исходное неравенство 5(3x − 9) имеет те же решения.
Ответ можно записать в виде числового промежутка:
В этом выражении говорится, что решениями неравенства 5(3x − 9) являются все числа от минус бесконечности до плюс бесконечности.
Пример 2. Решить неравенство: 31(2x + 1) − 12x > 50x
Раскроем скобки в левой части неравенства:
Перенесём 50x из правой части в левую часть, изменив знак. А член 31 из левой части перенесём в правую часть, опять же изменив знак:
Приведём подобные слагаемые:
Получили неравенство 0x > −31 . В левой части располагается произведение, которое будет равно нулю при любом x . А ноль больше, чем −31 . Значит решением неравенства 0x является любое число.
А если приведённое равносильное неравенство 0x > −31 имеет бесчисленное множество решений, то и исходное неравенство 31(2x + 1) − 12x > 50x имеет те же решения.
Запишем ответ в виде числового промежутка:
Задания для самостоятельного решения
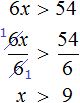

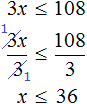

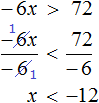

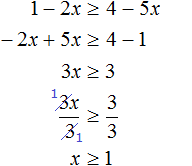

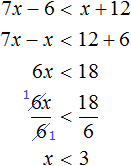

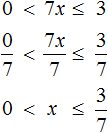

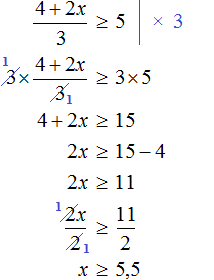

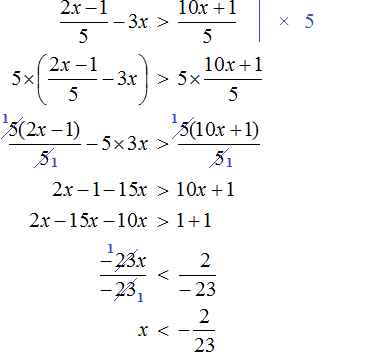

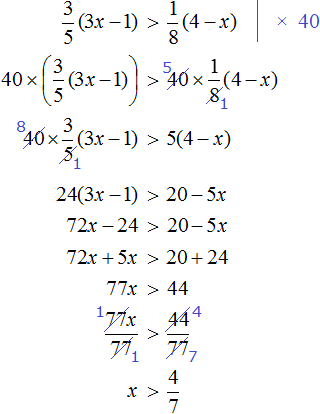

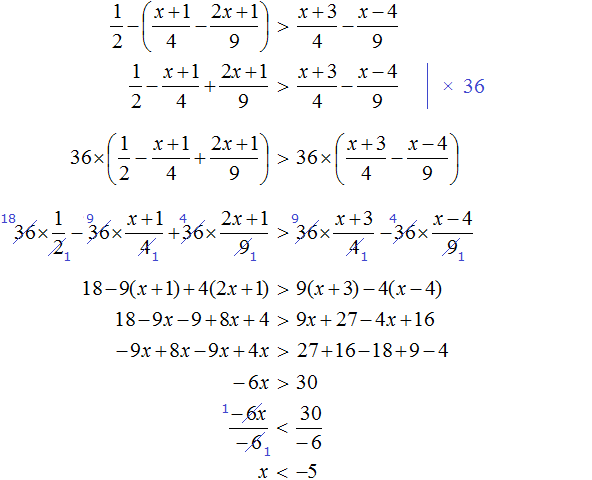

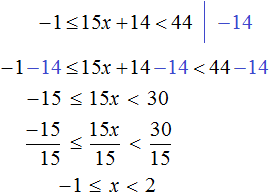

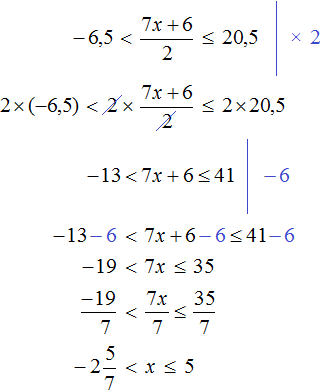

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

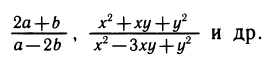
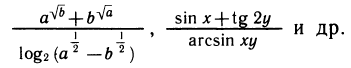
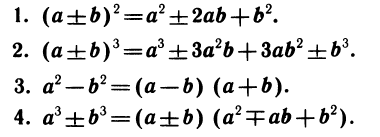
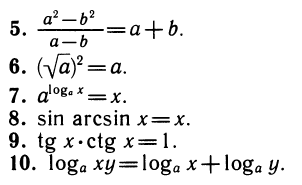


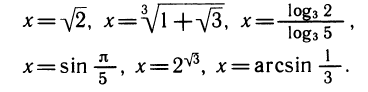
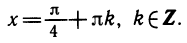
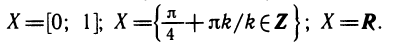
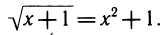
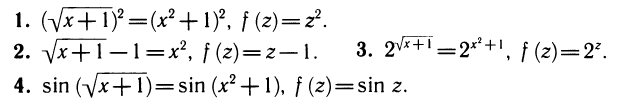
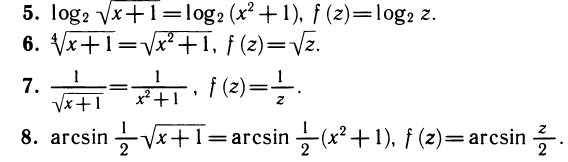
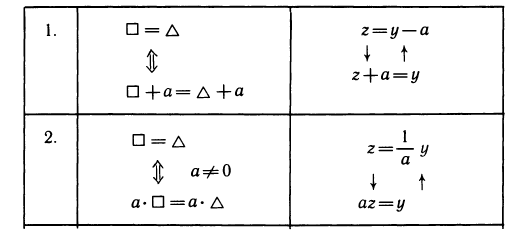
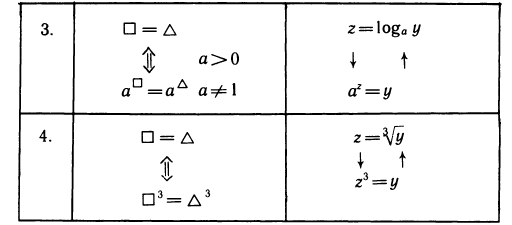
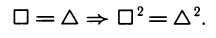
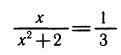
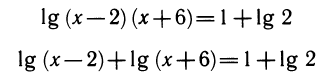
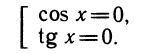
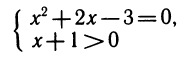
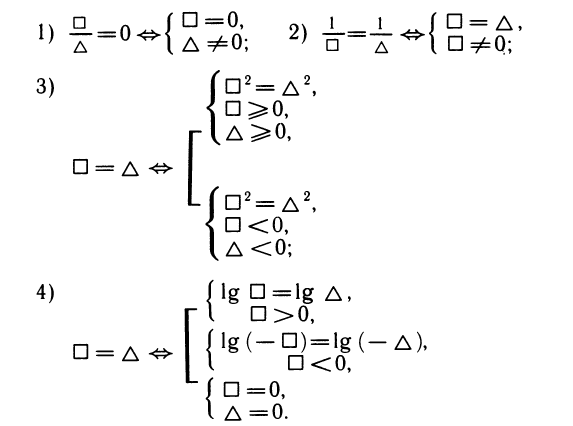
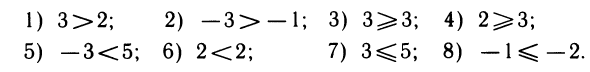
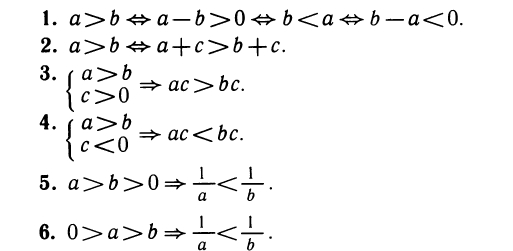
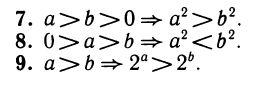
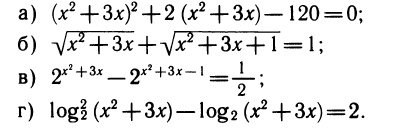
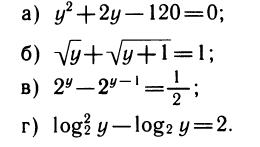
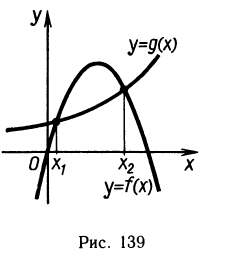
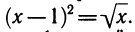
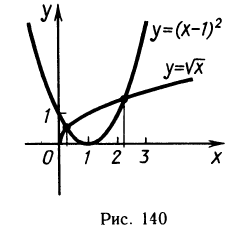
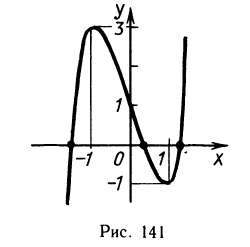
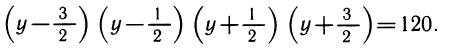
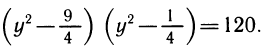
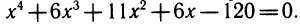
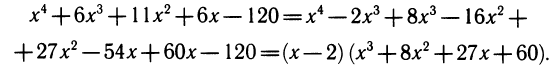
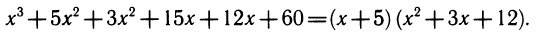
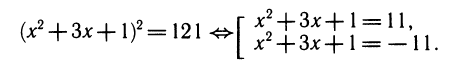
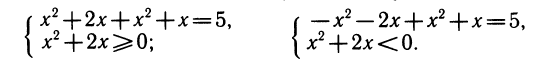
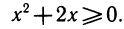
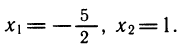
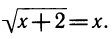
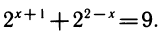
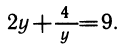
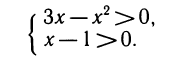
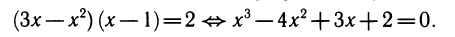
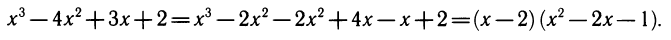
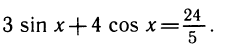
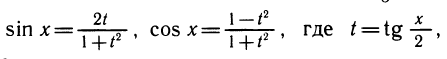
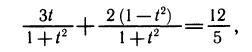
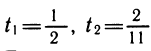
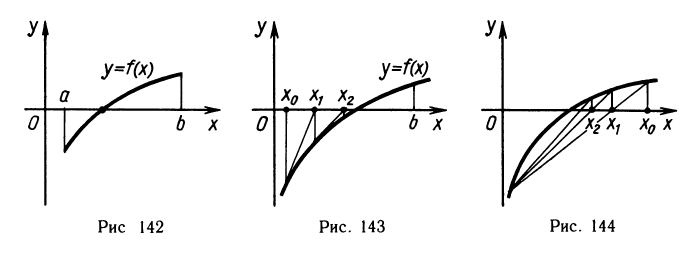
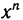 >а.
>а.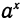 >Ь.
>Ь.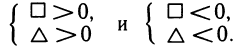
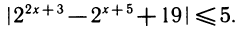
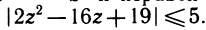
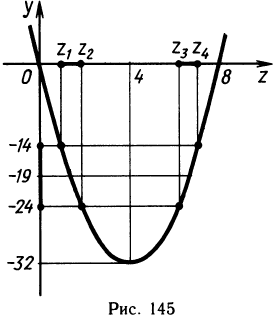
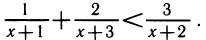
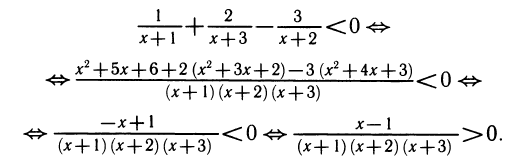
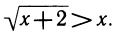
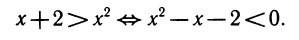
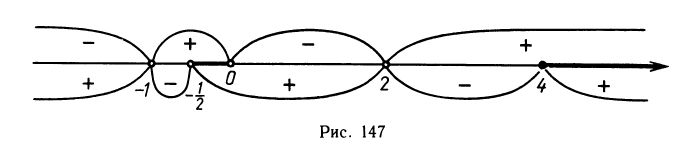
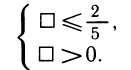
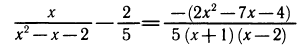
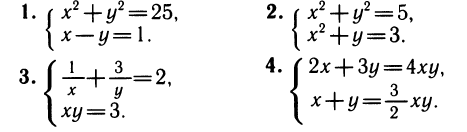
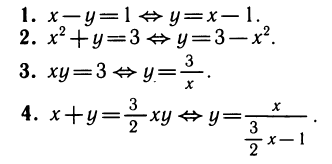
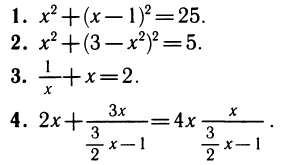
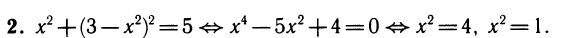
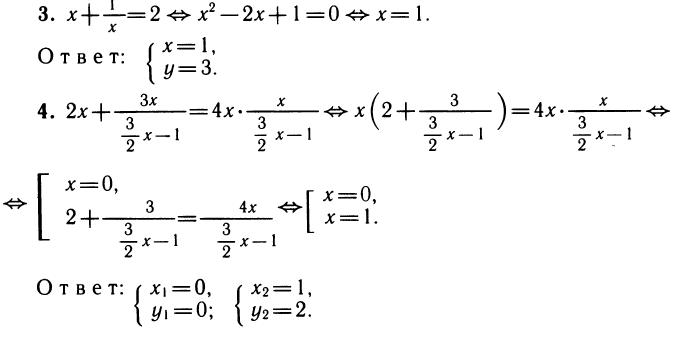
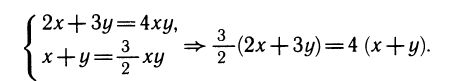
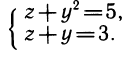
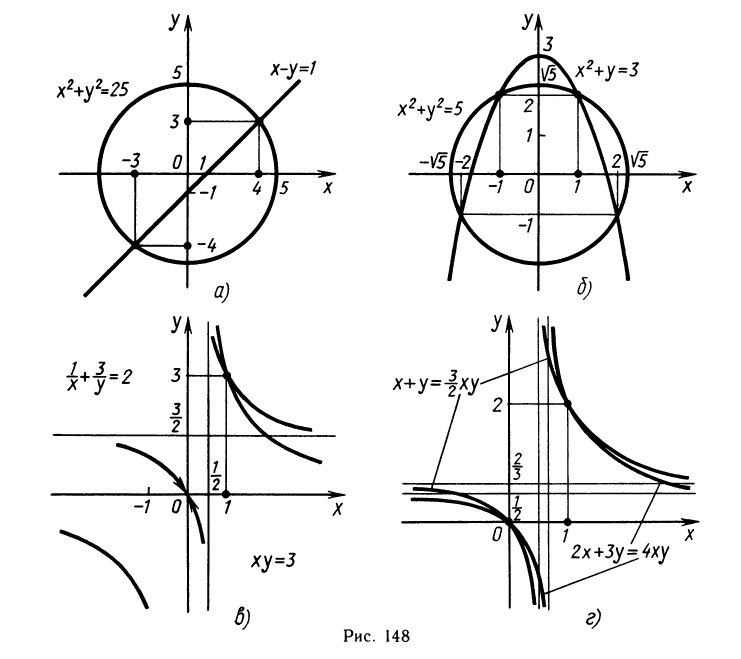
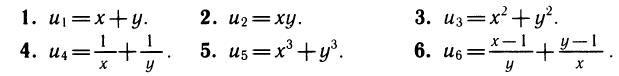
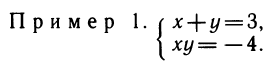
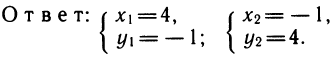
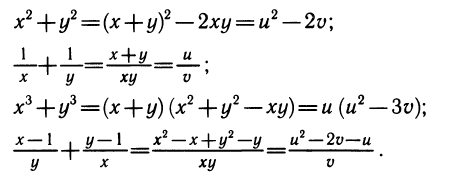
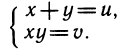
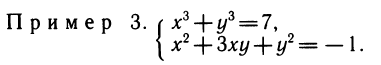
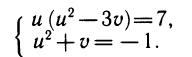
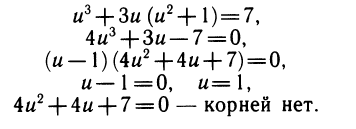
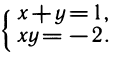
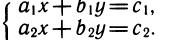
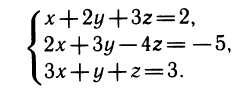
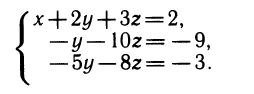
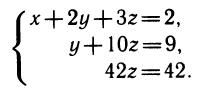

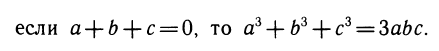
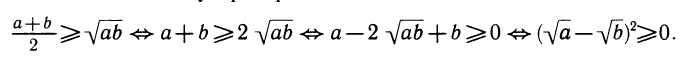
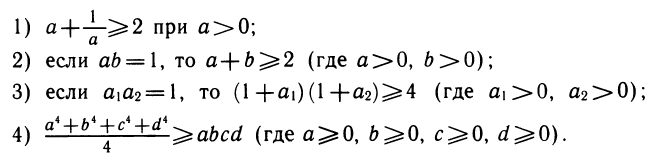
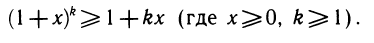
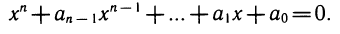
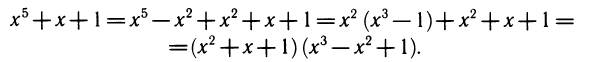
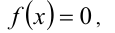
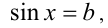
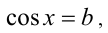
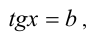
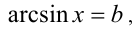
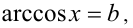

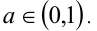
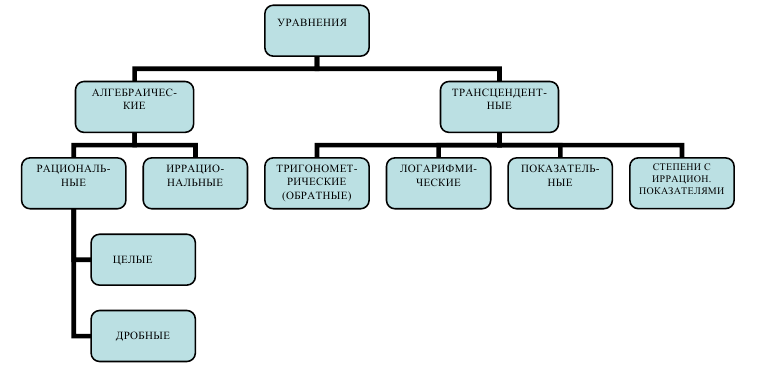
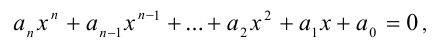
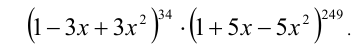
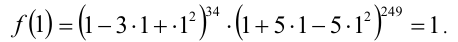
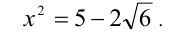
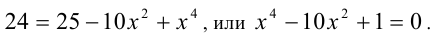
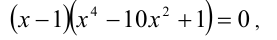
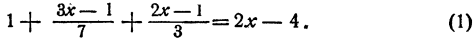
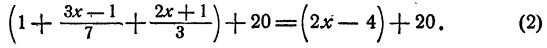


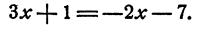
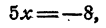
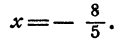
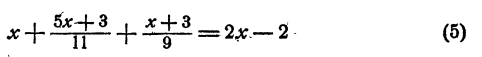
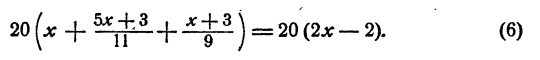
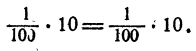
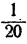


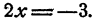
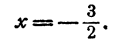
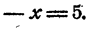
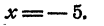
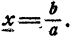
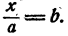


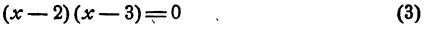
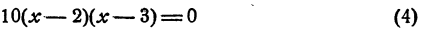

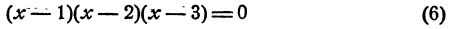

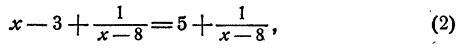


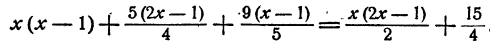
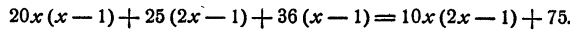
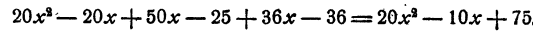
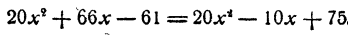
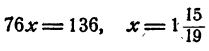
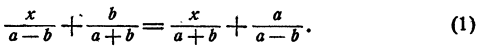
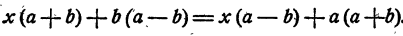
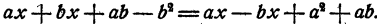
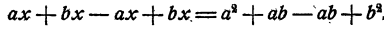
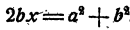
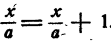
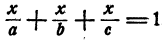
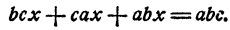
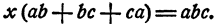
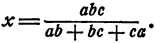
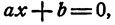
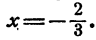 Пример. Уравнение 2x=0 имеет единственное решение х=0.
Пример. Уравнение 2x=0 имеет единственное решение х=0. х + 1 = 0не имеет решения, так как при любом значении хпроизведение 0
х + 1 = 0не имеет решения, так как при любом значении хпроизведение 0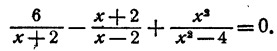
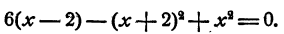
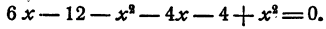
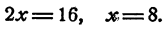
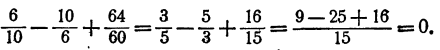
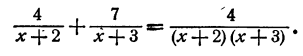
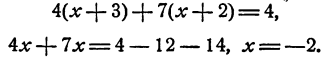
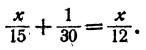
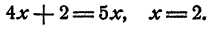
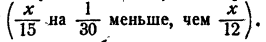 При составлении уравнения мы к меньшей из величин добавили соответствующее количество и полученную сумму приравняли большей. Вместо этого мы могли бы из большей величины вычесть соответствующее количество и полученную разность приравнять меньшей.
При составлении уравнения мы к меньшей из величин добавили соответствующее количество и полученную сумму приравняли большей. Вместо этого мы могли бы из большей величины вычесть соответствующее количество и полученную разность приравнять меньшей.