Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах.
Расчет симметричных режимов работы трехфазных систем
Многофазный приемник и вообще многофазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если 

Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется симметричным. В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол 

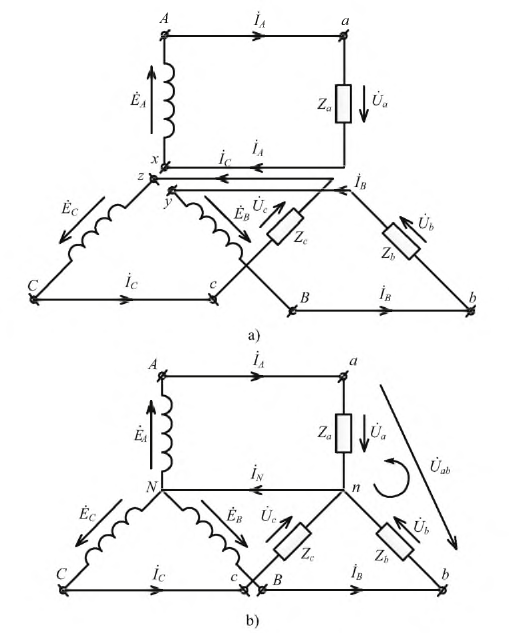
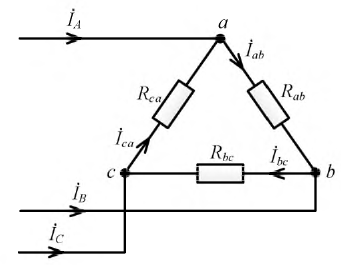
Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фаз 

где 

Тогда на основании вышесказанного


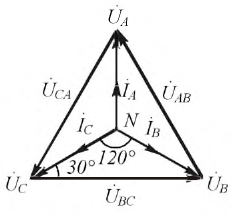
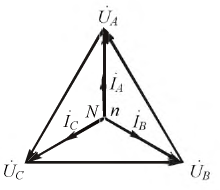
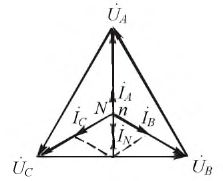
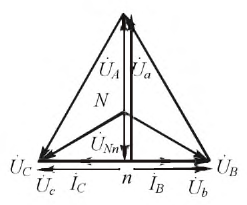
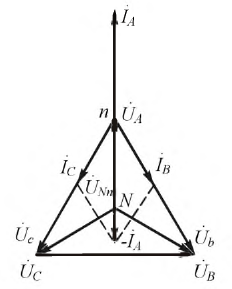
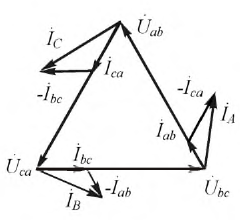
Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:
При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники симметричны, то в соответствии с формулами преобразования «треугольник-звезда» 
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении 


В соответствии с указанной методикой выделим расчетную фазу А, которая представлена на рис. 4. Здесь 

Тогда для тока 

и соответственно 
Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее.
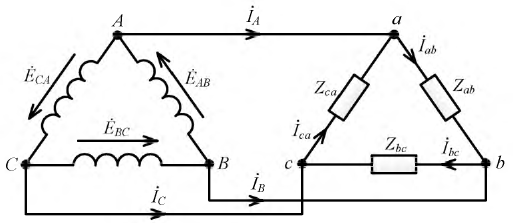
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные цепи при соединении в треугольник. Пусть в схеме на рис. 2,а 



По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:

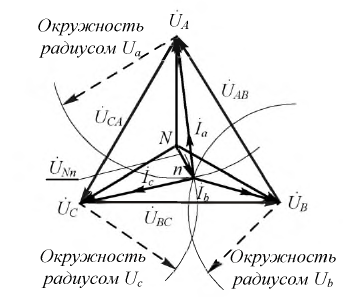
Обычно на практике известны не комплексы линейных напряжений, а их модули. В этом случае необходимо предварительное определение начальных фаз этих напряжений, что можно осуществить, например, графически. Для этого, приняв 
Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов:
При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет.
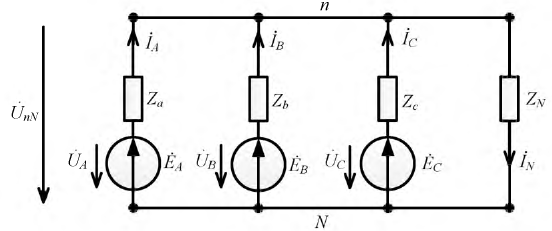
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной нагрузке 

Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением смещения нейтральной точки (обычно принимается, что 
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны:

Тогда для искомых токов можно записать:

Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид
 . . | (1) |
При наличии нейтрального провода с нулевым сопротивлением 





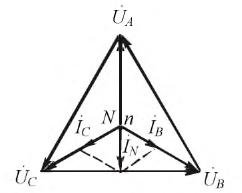
В качестве примера анализа несимметричного режима работы цепи с использованием соотношения (1) определим, какая из ламп в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если 
Запишем выражения комплексных сопротивлений фаз нагрузки:
Тогда для напряжения смещения нейтрали будем иметь
Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника опускается)
Таким образом, наиболее ярко будет гореть лампочка в фазе С.
В заключение отметим, что если при соединении в звезду задаются линейные напряжения (что обычно имеет место на практике), то с учетом того, что сумма последних равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например, 


 . . | (2) |
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой многофазный приемник является симметричным?
- Какой режим работы трехфазной цепи называется симметричным?
- В чем заключается специфика расчета симметричных режимов работы трехфазных цепей?
- С помощью каких приемов трехфазная симметричная схема сводится к расчетной однофазной?
- Что такое напряжение смещения нейтрали, как оно определяется?
- Как можно определить комплексы линейных напряжений, если заданы их модули?
- Что обеспечивает нейтральный провод с нулевым сопротивлением?
- В цепи на рис. 6,а
;
;
;
. Линейное напряжение равно 380 В.
Определить ток в нейтральном проводе.
Ответ: 
В схеме предыдущей задачи 

Определить ток в нейтральном проводе.
Ответ: 
В задаче 8 нейтральный провод оборван.
Определить фазные напряжения на нагрузке.
Ответ: 


В задаче 9 нейтральный провод оборван.
Определить фазные напряжения на нагрузке.
Ответ: 


- Трехфазные цепи
- Трехфазная система
- Соединение звездой
- Соединение треугольником
- Мощность трехфазных систем и ее измерение
- Сравнение трехфазных и однофазной cиcтем
- Пульсирующее и вращающееся магнитные поля
- Основы метода симметричных составляющих
- Трехфазные цепи
- Соединение обмоток генератора звездой
- Соединение обмоток генератора треугольником
- Соединение потребителей звездой
- Соединение потребителей треугольником
- Мощность трехфазного тока
- Топографическая диаграмма
- Вращающееся магнитное поле двухфазного тока
- Пульсирующее магнитное поле
- Определение трёхфазных цепей
- Трёхфазный генератор
- Способы соединения фаз генератора и нагрузки
- Соединение фаз генератора и нагрузки треугольником
- Режимы работы трёхфазных цепей
- Соединение «звезда-звезда» с нулевым проводом и без нулевого провода
- Соединение потребителей треугольником
- Расчет мощности в трёхфазных цепях
- Измерение мощности в трёхфазных цепях
- Соединение приемников по схеме четырехпроводной звезды
- Соединение приемников по схеме трехпроводной звезды или треугольником
- Метод симметричных составляющих
- Фильтры симметричных составляющих
- Трехфазные цепи
- Общие сведения о трёхфазных цепях
- Симметричный режим работы трёхфазной цепи
- Измерение мощности в трёхфазной цепи
- 📸 Видео
Видео:Трехфазные цепи. Схема соединения "ЗВЕЗДА"Скачать

Трехфазные цепи
Содержание:
Трехфазные цепи:
Многофазной системой называется совокупность электрических цепей, называемых фазами, в которой действуют синусоидальные напряжения одной частоты, отличающиеся друг от друга по фазе. Чаще всего применяются симметричные многофазные системы, напряжения которых равны по величине и сдвинуты по фазе на угол
Видео:Трехфазные цепи - Задача 1. Расчет трехфазной цепи соединенной звездойСкачать
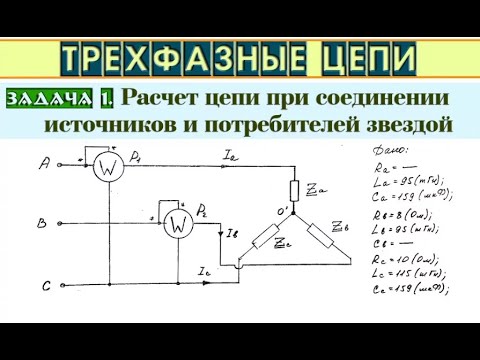
Трехфазная система
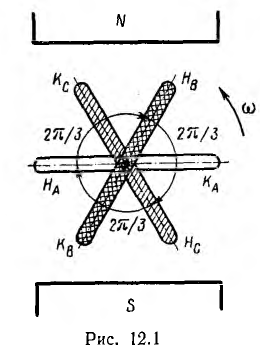
Наибольшее распространение имеет трехфазная система, созданная русским ученым М. О. Доливо-Добровольским (1891 г.); он изобрел и разработал все звенья этой системы — генераторы, трансформаторы, линии передачи и двигатели трехфазного тока.
Простейший трехфазный генератор (рис. 12.1) подобен рассмотренному в источнику однофазного напряжения; он состоит из трех одинаковых плоских витков или катушек, называемых фазами генератора, вращающихся в однородном магнитном поле с равномерной угловой скоростью ω вокруг оси, перпендикулярной к направлению магнитных линий. В каждой фазе следует различать начало и конец. Считая, что все катушки намотаны в одном направлении, например по часовой стрелке, можно принять за начало начальный зажим катушки или, наоборот, конечный, но принятое условие должно быть одинаковым для всех фаз. Цепи нагрузки подключаются к генератору с помощью щеток, наложенных на кольца, соединенные с катушками аналогично рис. 6.1 (на рис. 12.1 они не показаны).
Три фазы трехфазного генератора расположены под углом 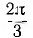
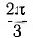
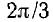
При вращении в фазах будут индуктироваться э. д. с.; период Т этих э. д. с. обороту. Катушки одинаковы, поэтому (амплитуды) э. д. с. фаз будут также одинаковы. Так как фазы сдвинуты друг относительно друга в пространстве на угол 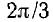
Если за начальный взять момент времени, когда плоскость первой катушки перпендикулярна линиям магнитной индукции (см. рис. 12.1), э. д. с. (отсчитываемая, например, от конца к началу)
и э. д. с. двух других катушек (отсчитываемые в том же направлении), отставая по фазе на углы 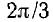
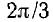
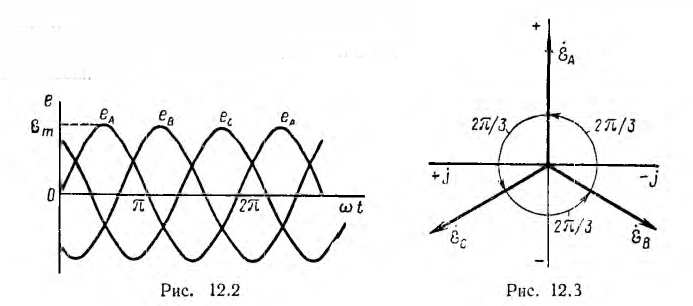
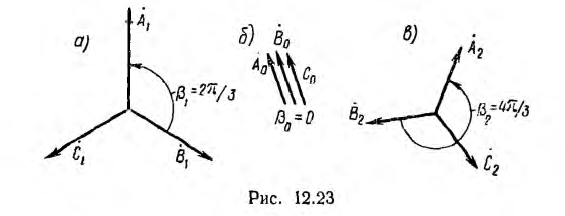
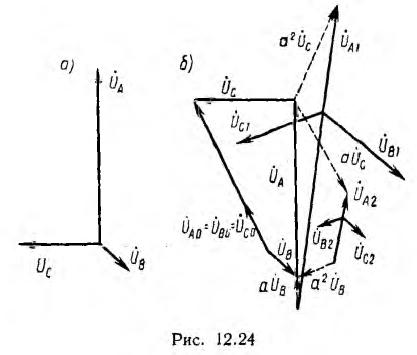
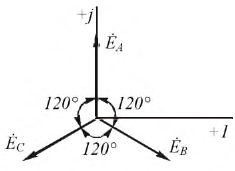
Временная диаграмма э. д. с. изображена на рис. 12.2. Если вектор э. д. с. первой фазы направить по оси вещественных комплексной плоскости (рис. 12.3), комплексы э. д. с. симметричной системы будут иметь вид:
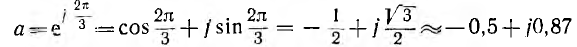
является оператором поворота вектора на угол 2π/3 в положительном направлении. Тогда
т. е. сумма векторов симметричной системы равна нулю. Это значит, что равна нулю в любой момент времени и алгебраическая сумма мгновенных значений, что можно видеть и из рис. 12.2, если взять сумму ординат трех синусоид для любой абсциссы.
Если в цепь каждой фазы генератора включить одинаковые по величине и характеру сопротивления (рис. 12.4), то токи фаз будут равны по величине и сдвинуты по фазе относительно своих напряжений на один и тот же угол ϕ:
Они также образуют трехфазную симметричную систему векторов.
При неодинаковой нагрузке фаз максимальные значения токов и фазные сдвиги будут различны, и система токов будет несимметричной.
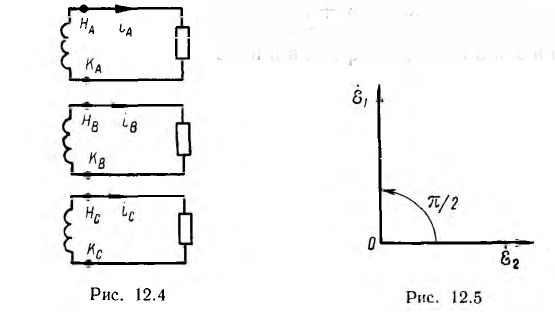
В электроизмерительной технике и автоматике применяется также двухфазная система, векторная диаграмма э д. с. которой показана на рис. 12.5. Хотя э. д. с. 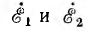
Показанная на рис. 12.4 несвязанная трехфазная система, при которой отдельные фазы не соединены между собой, на практике не применяется — генераторы и приемники связывают или в звезду, или в треугольник.
Соединение звездой
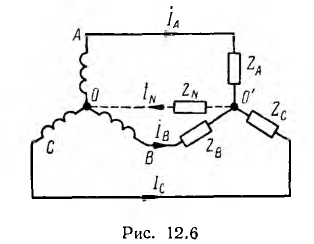
При соединении генератора звездой вместе соединяются концы фаз, образуя нулевую (нейтральную) точку 0. К началам фаз генератора с помощью трехпроводной линии передачи присоединяется приемник. Если последний также соединен звездой, нулевые точки генератора и приемника могут быть соединены нулевым (нейтральным) проводом (рис. 12.6).
Различают величины, относящиеся к фазам генератора и приемника — фазные напряжения и токи, и к линейным проводам — линейные напряжения и токи. Так как линейные провода соединены последовательно с фазами генератора и приемника, линейные токи в звезде равны соответствующим фазным токам.
Для получения симметричных соотношений между величинами следует выбирать положительные направления токов во всех фазах единообразно; обычно направляют токи от генератора к приемнику (см. рис. 12.6), т. е. в сторону движения энергии. В соответствии с аналогом закона Ома 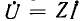
Если выбрать направление тока в нулевом проводе от нулевой очки приемника к нулевой точке генератора (см. рис. 12.6), мгновенное значение iN и комплекс IN этого тока в общем случае будут:
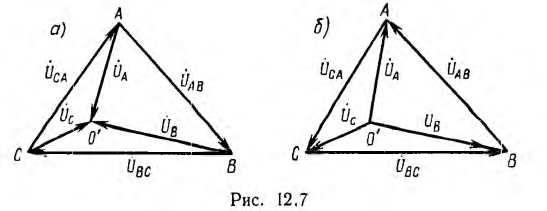
На рис. 12.7, а изображена диаграмма фазных напряжений на фиемнике в соответствии с принятым на рис. 12.6 направлением гоков, сходящихся в нулевой точке О’ приемника.
Эта диаграмма называется топографической, так как ее точкам А, В, С, О’ соответствуют одноименные точки цепи. Векторы и комплексные линейные напряжения 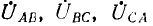
а их мгновенные значения
Из этих соотношений вытекает, что сумма линейных напряжений равна нулю.
Топографическая векторная диаграмма рис. 12.7, а, в которой векторы фазных напряжений сходятся в одной точке, соответствующей нулевой точке приемника, обычно заменяется диаграммой рис. 12.7, б, где эти векторы выходят из этой же точки; так как при этом все векторы фазных и линейных напряжений изменяют свои направления на обратные, приведенные выше соотношения между напряжениями сохраняются.
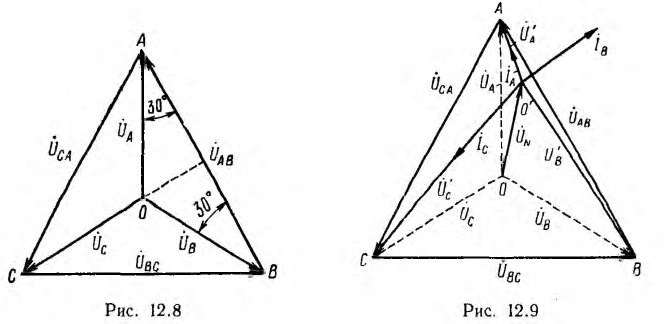
При симметричной системе фазных напряжений векторы линейных напряжений образуют равносторонний треугольник; нулевая точка совпадает с его центром тяжести (рис. 12.8) и линейное напряжение
г. е. по абсолютной величине линейные напряжения в 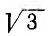
Далее сначала рассматриваются цепи без взаимной индукции между фазами и между фазами и нулевым проводом.
В звезде с нулевым проводом (см. рис. 12.6), если пренебречь его сопротивлением (ZN = 0), а также сопротивлением, линейных проводов, фазные напряжения приемника будут, очевидно равны фазным напряжениям генератора; их векторные диаграммы совпадут (см. рис. 12.7, б). Следовательно, фазные комплексные токи будут определяться фазными комплексными напряжениями генератора и комплексными сопротивлениями или проводимостями тех же фаз приемника:
т. е. соединение звездой с нулевым проводом без сопротивления обеспечивает независимую работу фаз.
При симметричной системе фазных напряжений и одинаковой нагрузке фаз система фазных токов будет симметричной и ток IN нулевого провода, равный сумме токов, будет также равен нулю независимо от величины сопротивления этого провода.
В звезде с нулевым проводом, имеющим сопротивление ZN в общем случае, когда 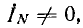
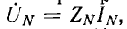
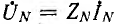
где 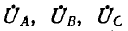
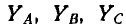
В звезде без нулевого провода YN =0 и
Фазные напряжения на приемнике и токи (см. рис. 12.9):
Выражения для узлового напряжения показывают, что 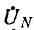
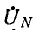
В случае звезды без нулевого провода фазные напряжения на приемнике могут быть выражены через линейные напряжения:
Выражения для 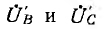
Приведенный вывод выражений для фазных напряжений на приемнике через фазные или линейные напряжения генератора справедлив для общего случая несимметричных систем фазных и линейных напряжений.
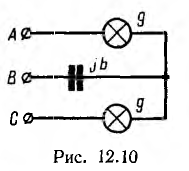
Примером неодинаковой нагрузки фаз может служить прибор для определения порядка следования фаз (рис. 12.10). Он представляет собой три одинаковые по величине проводимости, соединенные в звезду, — две лампы накаливания и конденсатор; тогда, считая, что проводимости ламп линейны,
где а — абсолютное значение проводимостей. При симметричной системе фазных напряжений генератора, если вектор UА направлен по оси вещественных величин (UA = U), узловое напряжение
Тогда комплексные напряжения на лампах будут:
На рис. 12.9 показана векторная диаграмма для рассматриваемой цепи. Векторы токов 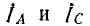
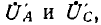
Действующие значения напряжений на лампах и их отношение будут:
Поэтому лампа, включенная в фазу С, будет светиться ярче лампы, включенной в фазу А, т. е. фазы следуют друг за другом в следующем порядке: яркая лампа, тусклая лампа, конденсатор.
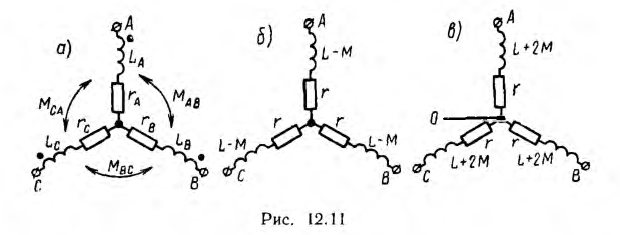
При индуктивных связях между фазами приемника и между его фазами и нулевым проводом должны быть учтены э. д. с. взаимной индукции. Так, например, для соединения звездой с нулевым проводом или без него по схеме рис. 12.11, а при взаимной индукции только между фазами уравнение по второму закону Кирхгофа для фазы А приемника будет иметь вид:
уравнения для второй и третьей фаз можно получить путем круговой перестановки индексов А, В, С.
Если нагрузка фаз одинакова, т. е.
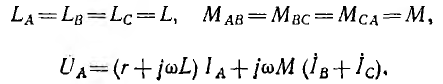
Если, кроме того, нулевой провод отсутствует или при его наличии система фазных напряжений симметрична, то сумма токов 1А + 1в + 1С=0, и уравнение (12.1) получит вид:
г. е. в этом случае цепь рис. 12.11, а эквивалентна схеме рис. 12.11, б без индуктивных связей, но с индуктивностью фаз приемника, равной L — М.
Для дальнейшего представляет интерес случай, когда есть нулевой провод, а все фазные напряжения генератора равны между собой и совпадают по фазе: 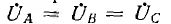
и уравнение (12.1) получит вид:
Это значит, что в данном случае цепь рис. 12.11, а эквивалентна схеме рис. 12.11, в без индуктивной связи, но с индуктивностью фаз приемника, равной L + 2М. Ток нулевого провода будет, очевидно, равен 3I.
Соединение треугольником
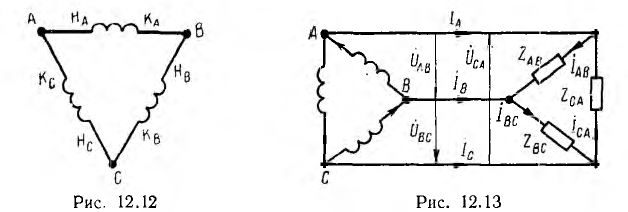
Чтобы соединить генератор в треугольник, нужно связать конец каждой фазы с началом следующей; в результате фазы генератора образуют замкнутый контур. При таком соединении симметричного генератора с отключенной нагрузкой (рис. 12.12) ток внутри него не возникает, так как сумма его э. д. c., образующих симметричную систему, равна нулю.
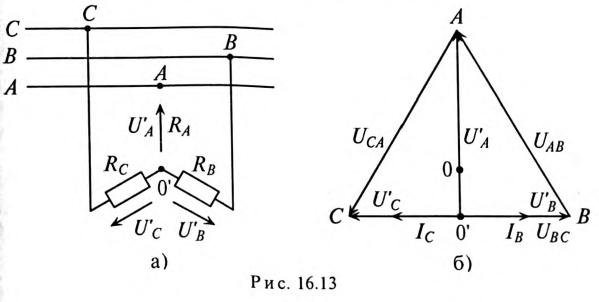
Соединив приемник также в треугольник (рис. 12.13), можно видеть, что фазные напряжения генератора и приемника одновременно являются и линейными, линейные же токи 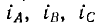
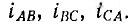
Для генератора соотношения между линейными и фазными токами аналогичны. Таким образом, линейные токи равны разностям соответствующих фазных токов.
Из полученных соотношений видно, что сумма линейных токов равна нулю:
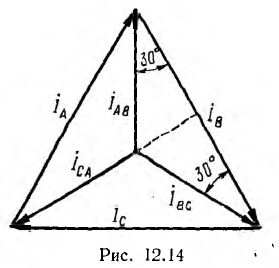
Для симметричной системы фазных токов (рис. 12.14)
т. е. по абсолютной величине линейные токи в 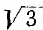
Токи в фазах приемника будут определяться линейными напряжениями и сопротивлениями или прово-димостями фаз приемника:
По приведенным соотношениям фазных токов могут быть определены линейные токи.
Если пренебречь сопротивлением проводов, напряжения генератора будут равны напряжениям приемника и фазы будут работать независимо друг от друга: всякое изменение сопротивления какой-либо фазы приемника вызовет изменение тока этой фазы и токов двух примыкающих к этой фазе линейных проводов, но никак не отразится на токах других фаз.
Если сопротивление линейных проводов не равно нулю (рис. 12.15, а), то из-за падения напряжения в них треугольник не обеспечивает независимой работы фаз. Изменение, например, сопротивления фазы АВ вызовет изменение фазного тока IAB, а следовательно, и линейных токов IА и IB. При этом изменятся падения напряжения в линейных проводах А и В, что при неизменных линейных напряжениях на зажимах генератора вызовет изменение напряжений на всех трех фазах приемника; следовательно, должны измениться также токи 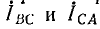
Для расчета цепи рис. 12.15, а при заданных линейных напряжениях, помимо методов уравнений Кирхгофа, наложения, контурных токов и узловых напряжений, при отсутствии взаимной индукции можно применить метод преобразования. Треугольник ZAB, ZBC. ZCA преобразуют в эквивалентную звезду ZA, ZB, Zc по формулам, соответствующим (рис. 12.15, б):
Объединяя в каждой фазе сопротивление линии и приемника, приводят схему к звезде (рис. 12.15, в), после определения токов которой возвращаются к цепи рис. 12.15, б, находя фазные и линейные напряжения на звезде ZA, ZB, Zc, а затем — к исходному треугольнику (см. рис. 12.15, а), чтобы найти его фазные токи.
Приведенные выше выражения для расчета соединения треугольником справедливы для общего случая несимметричной системы напряжений генератора.
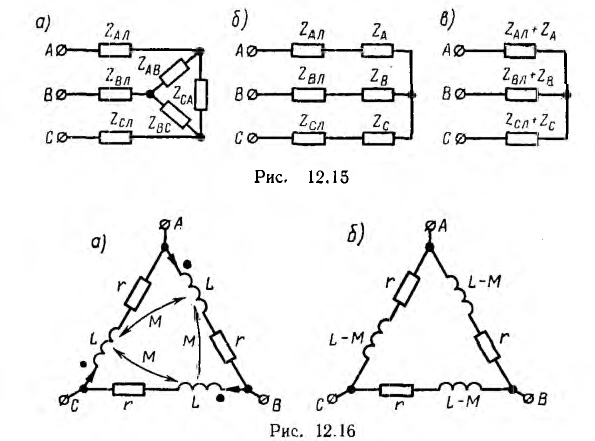
При наличии взаимной индукции, одинаковой нагрузке фаз и симметричной системе напряжений (рис. 12.16, а) система фазных токов будет также симметричной, тогда
и уравнение по второму закону Кирхгофа примет вид:
т. е. в этом случае цепь рис. 12.16, а эквивалентна схеме рис. 12.16, б без индуктивной связи, но с индуктивностью фаз приемника, равной L — М.
Мощность трехфазных систем и ее измерение
Мгновенная мощность трехфазной системы, как и всякой сложной цепи, равна сумме мощностей отдельных приемников, т. е. сумме мощностей фаз. Мгновенная мощность симметричной и одинакова нагруженной трехфазной системы
Сумма трех косинусоид, сдвинутых по фазе на угол 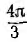
т. е. мгновенная мощность симметричной одинаково нагруженной трехфазной системы постоянна, тогда как мощность однофазной системы изменяется во времени с двойной частотой по сравнению с частотой напряжения и тока.
Многофазная система, мгновенная мощность которой постоянна, называется уравновешенной. Интересно отметить, что несимметричная двухфазная система с равными напряжениями (см. рис. 12.5) в случае одинаковой нагрузки фаз также является уравновешенной:
Из-за уравновешенности трехфазные и двухфазные двигатели имеют постоянный вращающий момент, тогда как момент однофазных двигателей пульсирует с двойной частотой.
Выражение для мощности уравновешенной трехфазной системы может быть преобразовано. В симметричной звезде
В симметричном треугольнике
В обоих случаях выражения для мощности получились одинаковыми.
Для измерения мощности трехфазной симметричной и одинаково нагруженной системы достаточен один ваттметр, включенный в одну из фаз и измеряющий ее мощность. Аналогично включается однофазный счетчик электрической энергии, Для получения мощности и, соответственно, энергии трехфазной системы показания этих приборов следует утроить.
В общем случае несимметричной системы и неодинаковой нагрузки мгновенная мощность р есть величина переменная, т. е. такая система является неуравновешенной. Средняя мощность этой системы равна сумме средних мощностей отдельных фаз:
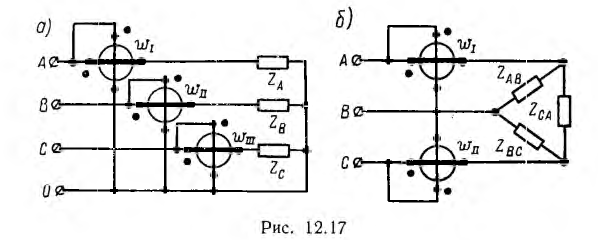
Следовательно, средняя мощность в данном случае может быть измерена тремя ваттметрами, включенными в каждую фазу, как это показано на рис. 12.17, а, для звезды с нулевым проводом (точками обозначены условные «начала» параллельных и последовательных цепей ваттметров).
В случае трех проводной системы можно ограничиться двумя ваттметрами, включенными так, как показано на рис. 12.17, б для измерения средней мощности трехфазной системы, соединенной треугольником. Мгновенные мощности, усредняемые первым и вторым ваттметрами, соответственно равны:
Так как 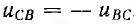
При переходе к средним мощностям получается, что сумма показаний ваттметров
т. е. равна мощности системы. Вывод справедлив и для звезды без нулевого провода, так как она может быть заменена эквивалентным треугольником.
Реактивная и полная мощности симметричной и одинаково нагруженной трехфазной системы равны суммам соответствующих мощностей всех фаз:
В общем случае несимметричной и неодинаково нагруженной трехфазной системы суммирование реактивных и полных мощностей фаз не дает величин, характерных для нагрузки генератора в целом, как это было в однофазной цепи с одним источником энергии. Предлагаемые в литературе определения реактивной и полной мощностей трехфазной несимметричной и неодинаково нагруженной системы чисто условны и потому здесь не рассматриваются.
Сравнение трехфазных и однофазной cиcтем
Сопротивление линейных и нулевого проводов, соединяющих генератор и приемник, обычно мало по сравнению с сопротивлением фаз приемника, и выводы, сделанные по поводу независимости работы фаз при соединении звездой и треугольником, можно обобщить следующим образом:
- в звезде с нулевым проводом и в треугольнике токи фаз практически мало зависят друг от друга и поэтому эти схемы следует применять при неодинаковой нагрузке фаз;
- звезда без нулевого провода может применяться только при одинаковой нагрузке фаз.
Необходимо отметить, что схема соединений генератора и приемника может быть различной, и один из них может быть соединен треугольником, другой — звездой без нулевого провода.
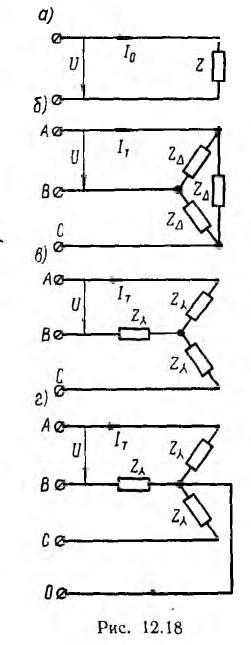
Представляет интерес сравнение расхода металла с удельным сопротивлением р на провода однофазной и трехфазной линий передачи (рис. 12.18) той же мощности Р на то же расстояние l при одинаковом cosϕ и том же к. п. д., т. е. тех же потерях в линии Рл = kP, где k — относительная потеря мощности, и одинаковом линейном напряжении U.
Для однофазной двухпроводной линии (рис. 12.18, а) Р = UI0 cosϕ; отсюда ток I0, потери Рл и сопротивление r0 одного провода:
Следовательно, сечение s0 и объем V0 проводов соответственно равны:
Отсюда видно, что формула для сечения двухпроводной линии переменного тока отличается от аналогичной формулы для линии постоянного тока наличием множителя 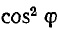
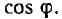
Для трехфазной трехпроводной линии (рис. 12.18, б и в) 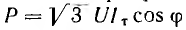
а сечение sT и объем VT проводов:
В знаменателе этих выражений также присутствует множитель 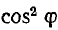
Из формул для s0 и sT видна эффективность высокого напряжения и большого коэффициента мощности — сечения обратно пропорциональны квадратам этих величин. Вместе с тем очевидно, что стоимость изоляции проводов растет с ростом напряжения. В результате экономически оптимальное напряжение U оказывается тем выше, чем больше передаваемая мощность Р и длина l линии.
Соотношение объемов металла линий: однофазной двухпроводной V0 и трехфазных —- трехпроводной Vr и четырехпроводной с нулевым проводом половинного сечения 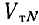
Таким образом, при одинаковом линейном напряжении звезда без нулевого провода и треугольник, очевидно, дают одинаковый расход металла на линию передачи и экономию в 25% по сравнению с однофазной линией, а нулевой провод половинного сечения вызывает перерасход металла, но все же система остается легче однофазной на 12,5%.
Соединение звездой с нулевым проводом имеет важное преимущество: помимо трехфазных приемников, рассчитанных на линейное напряжение, оно позволяет включать однофазные приемники и на линейное, и на фазное напряжение.
Если приемники работают при одинаковом фазном напряжении, линейное напряжение звезды будет в 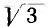
Основным преимуществом трехфазной системы по сравнению с однофазной является возможность легко создавать вращающееся магнитное поле, используемое, в частности, в трехфазных асинхронных двигателях, наиболее простых по конструкции и в эксплуатации.
Пульсирующее и вращающееся магнитные поля
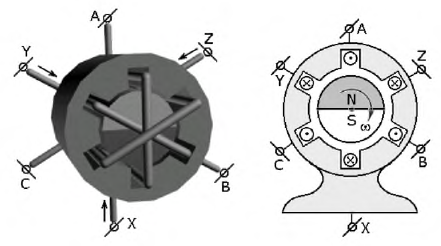
Электрические индуктивные машины переменного тока в большинстве случаев имеют магнитопровод в виде двух коаксиальных цилиндров, набранных из стальных листов и разделенных воздушным зазором (рис. 12 19). Внешний цилиндр S является статором, внутренний R — ротором.
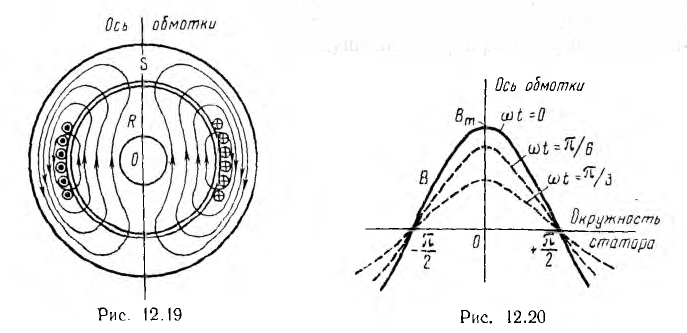
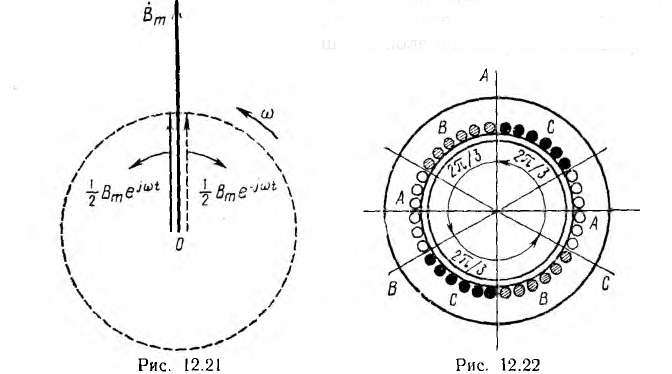
Если по обмотке статора, уложенной в его пазы н распределенной на части, например одной трети его окружности (рис. 12.19), будет проходить постоянный ток, магнитный поток, замыкающийся через статор, воздушный зазор и ротор будет постоянным. Приближенно магнитную индукцию можно считать распределенной по окружности статора по синусоидальному закону (сплошная линия на рис. 12.20); она имеет максимальные значения Вm по оси обмотки и равна нулю на нейтральной линии, перпендикулярной к оси обмотки. Такое синусоидально распределенное в зазоре машины поле можно условно изобразить постоянным вектором Вm (рис. 12.21), аналогично тому, как ранее это было сделано для величин, изменяющихся по синусоиде во времени.
Если по обмотке статора пропускать переменный ток, синусоидальное распределение магнитного поля сохранится, но поле будет пульсирующим, т. е. изменяющимся во времени по синусоидальному закону (см. рис. 12.20). Принимая за начало счета времени момент, когда индукция по оси обмотки максимальна, пульсирующее поле можно условно изобразить вектором 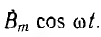
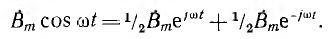
Это значит, что пульсирующее синусоидально распределенное поле может быть представлено в виде суммы двух также синусоидально распределенных полей 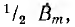
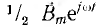
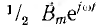
Разложение пульсирующего поля на два вращающихся используется, например, в однофазных двигателях, где прямое поле, воздействуя на ротор, приводит его во вращение, а обратное поле экранируется.
В трехфазных машинах на статор наложены три обмотки, показанные в разрезе на рис. 12.22, занимающие каждая треть его окружности; следовательно, эти обмотки и их оси сдвинуты в пространстве на угол 2π/3. Обмотки обтекаются токами, векторы которых образуют симметричную трехфазную систему. Тогда выражение для поля первой фазы А совпадает с выражением (12.2) при том же начале счета времени
Пусть обмотка, обтекаемая током второй фазы В, т. е. током, отстающим от тока первой фазы на угол 2π/3, сдвинута в пространстве вперед по направлению вращения прямого поля на тот же угол, что учитывается множителем 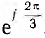
Аналогично записывается поле третьей фазы С, но так как она обтекается током, опережающим по фазе ток фазы А на угол 2π/3, и сдвинута в пространстве на тот же угол назад, знаки всех углов 2π/3 изменяются на обратные.
Результирующее поле определяется наложением полей всех трех фаз:
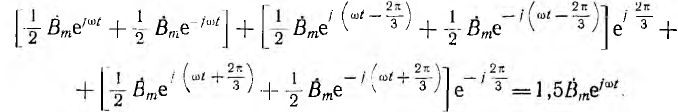
Отсюда видно, что все прямые поля трех обмоток арифметически складываются, тогда как обратные поля в сумме дают нуль и в машине возникает вращающееся поле, постоянное во времени. Амплитуда вращающегося поля в полтора раза превышает амплитуду пульсирующего поля отдельных обмоток, а фаза совпадает с фазой прямого поля обмотки первой фазы А.
В трехфазных двигателях вращающееся поле также используется для приведения во вращение ротора; из-за постоянства мощности в трехфазных системах и, следовательно, вращающего момента, а также отсутствия обратного поля эти двигатели имеют значительное преимущество перед однофазными.
Основы метода симметричных составляющих
Метод симметричных составляющих, предложенный Фортескью, позволяет сравнительно просто рассчитывать несимметричные, в частности, аварийные режимы в трехфазных системах и машинах. До предложения этого метода для таких расчетов надо было решать дифференциальные уравнения с переменными коэффициентами или оперировать с сопротивлениями, зависящими от токов.
В общем случае симметричной трехфазной системой векторов называется система, состоящая из трех равных по величине векторов, причем каждый вслед идущий вектор сдвинут относительно предыдущего на угол 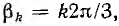
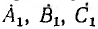
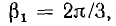
Симметричные системы линейных и фазных напряжений и токов, рассмотренные выше, были именно прямыми системами. Система 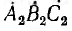
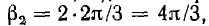
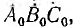
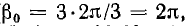
Система векторов, сдвинутых по фазе на угол 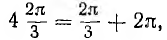
Пользуясь оператором 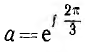
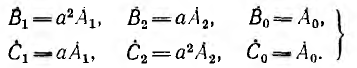
Пусть задана несимметричная система трех векторов А, В, С. Далее доказывается, что каждый вектор этой системы может быть представлен в виде суммы трех векторов, являющихся составляющими прямой, обратной и нулевой систем:
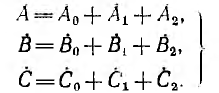
Подстановка уравнений (12.3) в уравнения (12.4) дает:
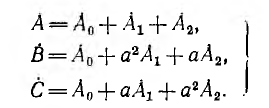
Система уравнений (12.5) решается относительно А0, А1, A2 однозначно:
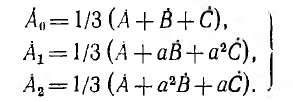
Отсюда и следует, что несимметричную систему векторов можно разложить на три симметричные системы.
Из первого уравнения системы (12.6) видно, что если сумма векторов несимметричной системы равна нулю, будут равны нулю и векторы нулевой системы. Следовательно, несимметричные системы линейных напряжений и линейных токов при отсутствии нулевого провода содержат только прямую и обратную составляющие.
Определение симметричных составляющих несимметричной системы векторов по выражениям (12.6) может быть выполнено также графически. Пусть задана несимметричная система векторов фазных напряжений 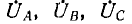
Далее очевидным построением определяются все векторы трех симметричных систем.
Аналогично производится разложение несимметричной системы токов.
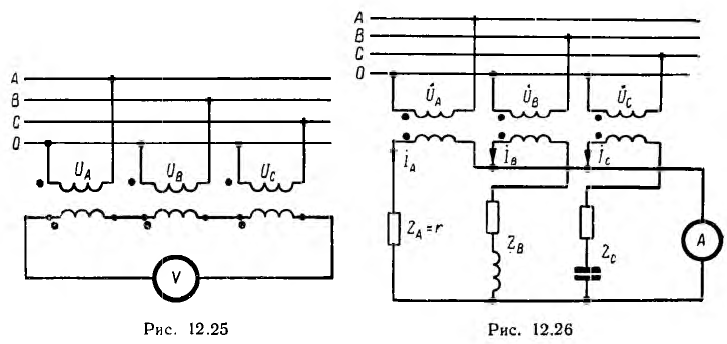
Симметричные составляющие несимметричной трехфазной системы напряжений и токов могут быть определены экспериментально. Например, для измерения нулевой составляющей системы фазных напряжений надо однообразно включить на фазные напряжения трансформаторы малой мощности, вторичные обмотки которых и вольтметр соединяются последовательно (рис. 12.25). Тогда, считая для простоты, что у трансформаторов коэффициент трансформации напряжения равен единице, суммарное напряжение, измеряемое вольтметром,
т. е. пропорционально напряжению нулевой системы.
Для измерения напряжения прямой последовательности (рис. 12.26) трансформаторы включаются на одинаковые по величине полные сопротивления z — трансформатор фазы А на активное сопротивление ZA=r, фазы В на активно-индуктивное сопротивление 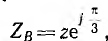
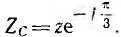
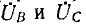
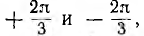
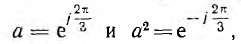
Цепи нагрузок всех трех трансформаторов соединяются параллельно и замыкаются на амперметр. Последний измеряет суммарный ток
пропорциональный напряжению U1 системы прямой последовательности.
Если поменять местами нагрузки фаз В и С, суммарный ток
будет пропорционален напряжению U2 системы обратной последовательности.
Рассмотренные схемы называются фильтрами симметричных составляющих. Они применяются в схемах защиты трехфазных энергетических систем от аварийных режимов, вызывающих несимметрию токов и напряжений отдельных фаз.
Разложение на симметричные составляющие позволяет весьма просто решать задачи на расчет трехфазных цепей при одинаковой нагрузке фаз с взаимной индукцией между ними при несимметричной системе напряжений, что широко используется в теории электрических машин. Система напряжений разлагается на симметричные составляющие, для каждой из них находят токи фаз и применяют метод наложения. При этом сопротивление фаз приемника для каждой составляющей может быть различным. Например, для цепи рис. 12.11, соединенной в звезду с нулевым проводом, сопротивление фаз для нулевой системы напряжений:
а для прямой и обратной составляющих, являющихся симметричными трехфазными системами, сопротивления
только для статических устройств, например для трансформаторов. Во вращающихся машинах прямая система токов создает магнитное поле, вращающееся в одном направлении с ротором, а обратная система токов — в противоположном; это приведет к неравенству 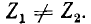
После определения комплексных токов каждой составляющей они пофазно суммируются и дают систему действительных токов фаз.
При неодинаковой нагрузке фаз приемника расчет усложняется, так как тогда каждая из симметричных составляющих системы такое зависит от всех составляющих систем напряжений. Эти задачи рассматриваются в литературе, посвященной расчету аварийных режимов в трехфазных электрических сетях и системах.
Можно показать, что в самом общем случае несимметрии средняя мощность всей цепи равна сумме средних мощностей нулевой, прямой и обратной составляющих:
Видео:Трехфазные электрические цепи │Теория ч. 1Скачать

Трехфазные цепи
Трехфазная система ЭДС:
Производство, передача и распределение электрической энергии осуществляется в основном трехфазным током в трехфазных цепях. Широкое распространение в качестве нагрузки в трехфазных цепях получили трехфазные потребители. В трехфазных цепях используются трехфазные трансформаторы. Электрическую энергию в трехфазных цепях производят трехфазные генераторы, создающие синусоидальные ЭДС одинаковой частоты, в трехфазных системах.
Трехфазной называется система трех ЭДС одинаковой частоты, Вдвинутых друг относительно друга по фазе так, что сумма углов сдвига равна 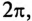
Трехфазная система ЭДС называется симметричной, если ЭДС трех фаз сдвинуты друг относительно друга на угол 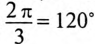
Комплексы этих ЭДС
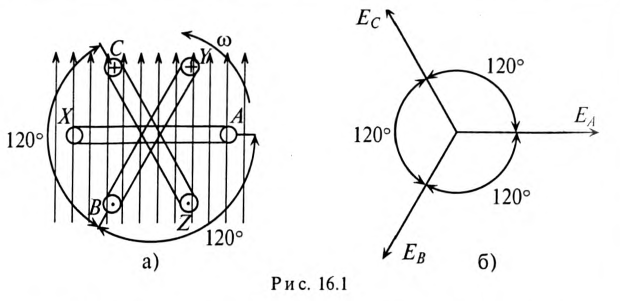
Получение симметричной трехфазной системы ЭДС осуществляется в трехфазном электромашинном генераторе (рис. 16.1а), в Котором три жестко скрепленные под углом 120° обмотки пересекают магнитное поле с частотой 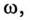
Начала обмоток трехфазного генератора обозначаются прописными буквами 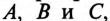
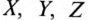
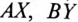
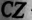
Таким образом, при вращении в магнитном поле жестко скрепленных обмоток в них индуктируются одинаковые ЭДС 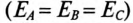
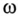
Векторная диаграмма такой симметричной системы ЭДС изображена на рис. 16.1б. Как видно из векторной диаграммы, мгновенное значение ЭДС в обмотке CZ можно записать в виде
а комплекс этой ЭДС
т. е. логично, чтобы начальная фаза 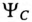
К каждой обмотке трехфазного генератора может быть подключена нагрузка с сопротивлениями
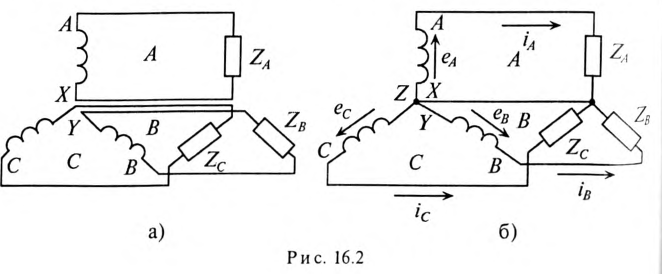
Если при этом три обмотки генератора электрически не соединены (рис. 16.2а), то такая трехфазная система называется несвязанной. Несвязанная трехфазная система практического применения не нашла.
Практическое применение нашла связанная трехфазная система (рис. 16.2б). Эта система экономически и энергетически более рациональна, так как используется три или четыре соединительных провода вместо шести и получить можно два различных напряжения, фазное и линейное, вместо одного.
Каждая обмотка трехфазного генератора со своей нагрузкой и соединительными проводами называется фазой (рис. 16.2). В трехфазной системе различают три фазы А, В и С (международные обозначения — прописные буквы).
Положительное направление ЭДС и токов в каждой фазе на рис. 16.26 указаны стрелками.
В связанных трехфазных системах применяется соединение обмоток генератора и потребителя звездой F или треугольником Е.
Соединение обмоток генератора звездой
При соединении обмоток генератора звездой концы обмоток X, Yи Z элeктpичecки соединяются в одну точку 0 (рис. 16.3а), которая называется нулевой, или нейтральной. При этом генератор с потребителем соединяется тремя или четырьмя проводами.
Провода, подключенные к началам обмоток генератора (А, В и С, называют линейными проводами, а провод, подключенный к нулевой точке 0, называется нулевым, или нейтральным. 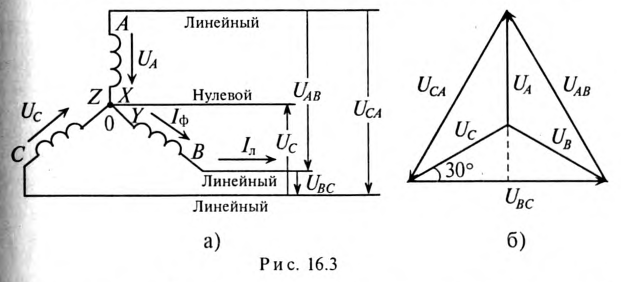
В связанных трехфазных системах различают фазные и линейные напряжения и токи.
Фазным называется напряжение между началом и концом обмотки генератора или между нулевым и линейным проводом. Обозначаются фазные напряжения прописными буквами с индексами фаз 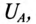
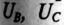
Линейным называется напряжение между началами обмоток генератора или между линейными проводами. Обозначаются линейные напряжения 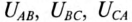
Можно определить зависимость между линейными и фазными напряжениями при соединении обмоток генератора звездой.
Мгновенные значения фазных напряжений равны разностям потенциалов между началами и концами соответствующих обмоток, т.е:
Мгновенные значения, линейных напряжений равны разностям потенциалов между началами соответствуют:
Потенциалы концов обмоток одинаковы 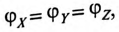
То есть мгновенное значение линейных напряжений определяется разностью мгновенных значений двух соответствующих фазных напряжений.
При соединении обмоток генератора звездой действующее значение линейного напряжения определяется геометрической разностью двух соответствующих фазных напряжений. На этом основании построена векторная диаграмма напряжений (рис. 16.3б) для соединения обмоток генератора звездой. К такому же результат) приводит определение комплексов линейных напряжений символическим методом:
При симметричной системе ЭДС фазные напряжения равны по величине 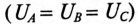
Линейное напряжение 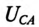
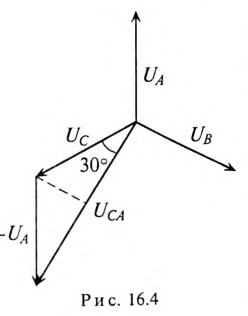
Из диаграммы (рис. 16.4) определяется вектор (комплекс)
При симметричной системе ЭДС линейное напряжение трехфазного генератора, обмотки которого соединены звездой, в 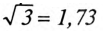
Если говорят о напряжении генератора 127/220 В, то имеется в виду, что фазное напряжение в трехфазной цепи 127 В, а линейное — 220 В. В сети с напряжением 220/380 В фазное напряжение 220 В, а линейное — 380 В. Очевидно, что обмотки генератора такой симметричной цепи соединены звездой и отношение напряжений получится равным
В связанных трехфазных системах фазным называется ток, провидящий по обмотке (фазе) генератора 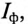
Как видно на рис. 16.3а, при соединении обмоток генератора звездой линейный ток 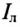
Соединение обмоток генератора треугольником
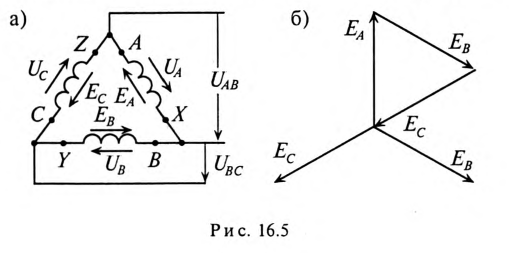
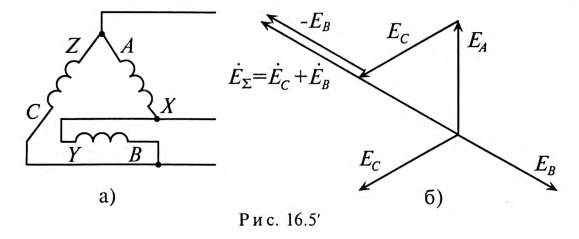
При соединении обмоток генератора треугольником (рис. 16.5а) конец обмотки фазы А соединяется с началом обмотки фазы В, конец обмотки фазы В соединяется к началом обмотки фазы С, конец обмотки фазы С соединяется с началом обмотки фазы А и к точкам соединения подключаются линейные провода.
При соединении обмоток генератора треугольником (рис. 16.5а) трехфазная цепь трехпроводная.
Как следует из схемы соединения обмоток треугольником (рис. 16.5а), линейное напряжение 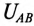
То есть
Из схемы (рис. 16.5а) следует, что три обмотки генератора, соединенные треугольником, образуют замкнутый контур, ток в котором при отсутствии нагрузки (холостой ход) определяется выражением
где 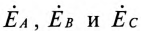
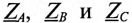
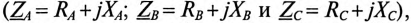
Так как сопротивления обмоток малы, падением напряжения на них можно пренебречь и считать, что напряжение на каждой обмотке генератора равно ее ЭДС.
При симметричной системе ЭДС и правильном соединении обмоток генератора треугольником (рис. 16.5а) геометрическая сумма ЭДС (комплексов) обмоток генератора, образующих замкнутый контур, равна нулю (рис. 16.5б). Следовательно, и ток в замкнутом контуре обмоток, соединенных треугольником, также равен нулю 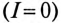
Если обмотки симметричного генератора соединены «неправильным» треугольником, т. е. неправильно подключить начало и конец хотя бы одной из обмоток, например 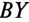
Соединение потребителей звездой
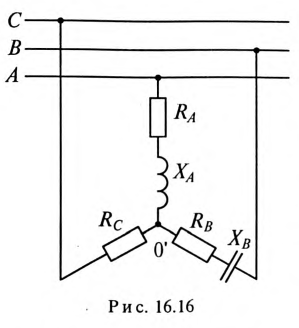
При соединении звездой потребителя и генератора (рис. 16.6) трехфазная система представляет собой сложную цепь с двумя узловыми точками 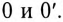
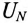
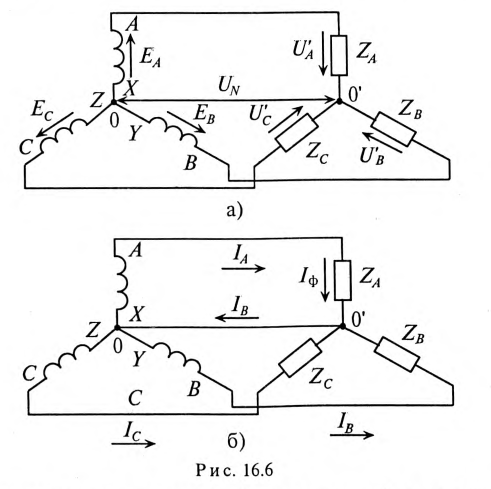
Соединение генератора и потребителя звездой может быть с нулевым проводом (рис. 16.6б), т.е. четырехпроводная цепь, и без нулевого провода (рис. 16.6а), т.е. трехпроводная цепь.
Величину напряжения смещения нейтрали 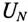
где 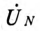
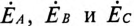
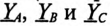
где 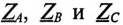
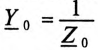
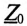
Напряжение U’ на каждой фазе потребителя, соединенного звездой (рис. 16.6а), с учетом напряжения смещения нейтрали, определяют следующим образом:
где 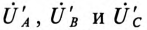
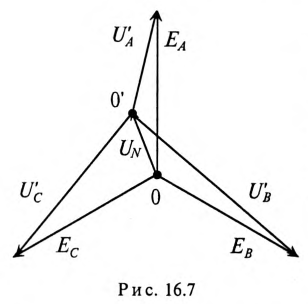
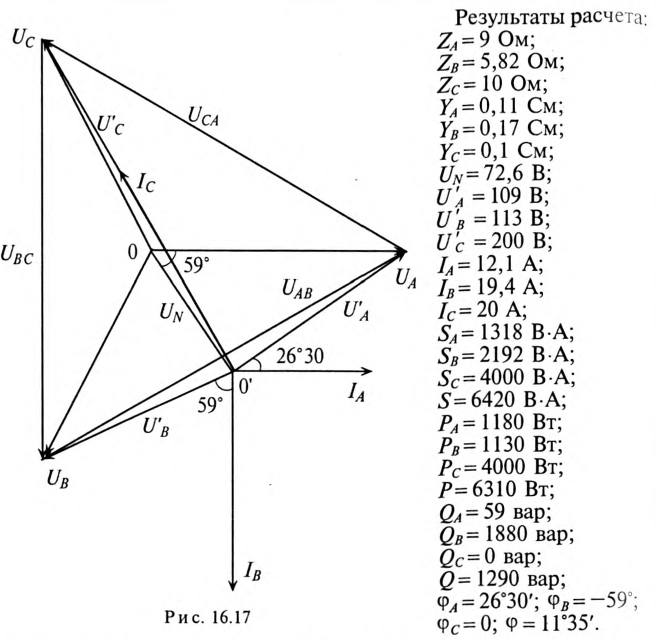
На основании (16.15) строится векторная диаграмма напряжений (рис. 16.7), на которой вектор напряжения смещения нейтрали взят произвольно. Из векторной диаграммы (рис. 16.7) следует, что при наличии напряжения смещения нейтрали напряжения на фазах потребителя, соединенного звездой, различны по величине и по начальной фазе даже при симметричной системе ЭДС в обмотках генератора.
Очевидно (рис. 16.7), что напряжения на фазах потребителя, соединенного звездой, будут одинаковыми по величине 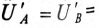
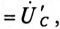
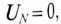
Напряжение смещения нейтрали отсутствует, т. е. 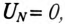
Рассмотрим эти условия:
1. Равномерная нагрузка фаз.
Равномерной называют нагрузку, при которой комплексы сопротивлений фаз равны между собой.
То есть
или
Тогда 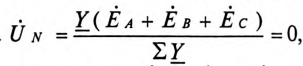
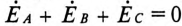
Так как комплекс сопротивления фазы 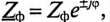
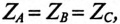
2. Наличие нулевого провода.
При наличии нулевого провода, соединяющего нейтральные точки 0 и 0′ (рис. 16.6б),
Тогда
В обоих случаях (1 и 2) напряжения на фазах потребителя, подключенного к трехфазному генератору с симметричной системой ЭДС, одинаковы по величине. При этом величина напряжения 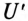
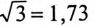
Ток в нулевом проводе 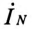
Токи в фазах потребителя определяются по формулам
Очевидно, что при равномерной нагрузке фаз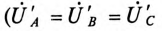
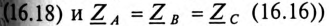
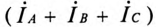
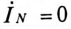
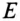
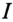
Таким образом, при равномерной нагрузке фаз нулевой провод не нужен.
При неравномерной нагрузке фаз отсутствие нулевого провода приводит к неодинаковым по величине напряжениям на каждой фазе потребителя (рис. 16.7). При этом на фазе с большим сопротивлением Z будет большее напряжение U’.
Так как отсутствие нулевого провода при неравномерной нагрузке фаз потребителя, соединенного звездой, нарушает режим работы потребителей U’, то предохранитель в нулевой провод не ставят.
Следовательно, нулевой провод служит для выравнивания напряжений на фазах потребителя при неравномерной нагрузке фаз.
При соединении потребителей звездой ток каждой фазы потребителя 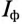
Соединение потребителей треугольником
При соединении потребителя треугольником (рис. 16.8) к каждой фазе потребителя приложено линейное напряжение трехфазной цепи
Так как при симметричной системе ЭДС все линейные напряжения равны по величине и сдвинуты на угол 120° по фазе, то и напряжения на каждой фазе потребителя, соединенного треугольником, равны по величине 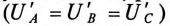
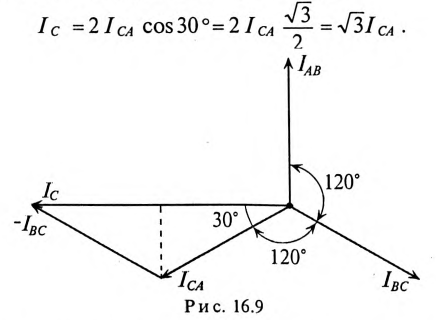
При соединении потребителей треугольником линейные токи обозначаются прописными буквами с индексами фаз, т. е. 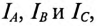
Воспользовавшись первым законом Кирхгофа, линейные токи можно определить выражениями (рис. 16.8)
Линейный ток при соединении потребителей треугольником определяется геометрической разностью двух фазных токов, сходящихся с линейным в одной узловой точке (рис. 16.8).
Фазные токи потребителя, соединенного треугольником, определяются:
При симметричной системе ЭДС генератора 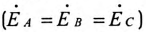
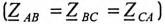
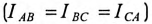
Таким образом, при равномерной нагрузке фаз и симметричной системе ЭДС при соединении потребителей треугольником линейный ток в трехфазной цепи в 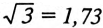
Мощность трехфазного тока
Активная мощность, отдаваемая трехфазным генератором и потребляемая трехфазным потребителем, определяется суммой активных мощностей каждой фазы потребителя:
Аналогичное определение можно отнести и к реактивной мощности трехфазного тока, т. е.
Полная, или кажущаяся, мощность трехфазного потребителя равна

Очевидно, что при равномерной нагрузке фаз 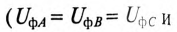
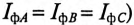
Однако на практике удобней оперировать линейными величинами, так как доступными являются линейные провода, а не обмотки генератора или двигателя.
При соединении потребителя звездой при равномерной нагрузке фаз
Тогда
При соединении потребителей треугольником при равномерной нагрузке фаз
Тогда
Таким образом, при равномерной нагрузке фаз при соединении потребителей звездой и треугольником мощности трехфазного тока определяются выражениями:
При неравномерной нагрузке фаз полная, или кажущаяся, мощность трехфазного тока может быть определена суммой полных мощностей каждой фазы, выраженной в комплексной форме, а именно
Равномерную нагрузку в трехфазных цепях обеспечивают электрические двигатели трехфазного тока, обмотки которых могут гь соединены или звездой, или треугольником.
Топографическая диаграмма
Напряжение между отдельными точками трехфазной цепи можно найти графически путем построения так называемой топографической диаграммы.
Топографическая диаграмма — это векторная диаграмма, поенная так, чтобы каждой точке цепи соответствовала определенная точка на диаграмме и чтобы вектор, проведенный в эту точку из начала координат, выражал по величине и фазе потенциал соответствующей точки цепи. Отрезок, соединяющий любые две точки на этой диаграмме, определяет напряжение между соответствующими точками цепи. Если топографическая диаграмма встроена в определенном масштабе, то по ней можно определить искомое напряжение и ток по величине и по фазе.
При построении топографической диаграммы для трехфазной цепи удобно принять за точку с нулевым потенциалом нулевую, или нейтральную, точку генератора. Этой точке генератора соответствует начало координат топографической диаграммы.
Топографическая диаграмма для трехфазной цепи, изображенной на рис. 16.6, построена при условии, что точка 0 на диаграмме (рис. 16.10) соответствует нулевой точке генератора, потенциал которой равен нулю, т. е.
Из точки 0 откладываются в определенном масштабе напряжений 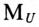
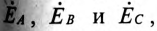
Отрезок 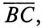
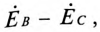
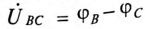
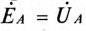
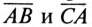
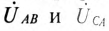
Отложив из точки 0 (начало координат) вектор напряжения смещения нейтрали 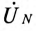
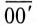
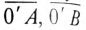
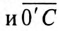
Если напряжение смешения нейтрали 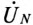
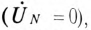
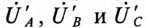
Применение топографической диаграммы для расчета трехфазной цепи рассмотрено в примере 16.1 настоящей главы.
Пример 16.1
К трехфазной трехпроводной сети с линейным напряжением 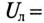
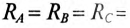
Определить напряжение и ток каждой фазы потребителя в каждом из трех режимов:
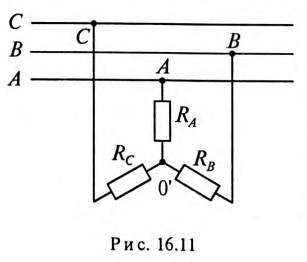
1. Потребители соединены звездой, как показано на рис. 16.11.
2. Обрыв в фазе А, т. е.
3. Короткое замыкание в фазе А, т. е.
Решение
Решение этой задачи производится с помощью построения топографической диаграммы для каждого режима.
1. Так как в данном режиме имеет место равномерная нагрузка фаз 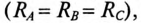
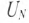
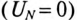
Пренебрегая внутренним сопротивлением обмоток генератора 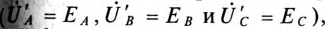
так как
Toк каждой фазы потребителя будет равен
Линейные токи в каждом линейном проводе также равны между собой и равны фазным токам каждой фазы, т.е.
2. При обрыве в фазе А схема трехфазной цепи обретает следующий вид (рис. 16.13а), а топографическая диаграмма показана на рис. 16.13б.
Таким образом, точка 0′ на топографической диаграмме при обрыве в фазе А как бы опустилась на вектор линейного напряжения 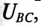
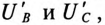
Напряжение на оборванной фазе А, т. е. напряжение между точками 0′ и А в схеме, как следует из топографической диаграммы рис. 16.13б), будет равно
Токи в фазах:
Токи в линейных проводах:
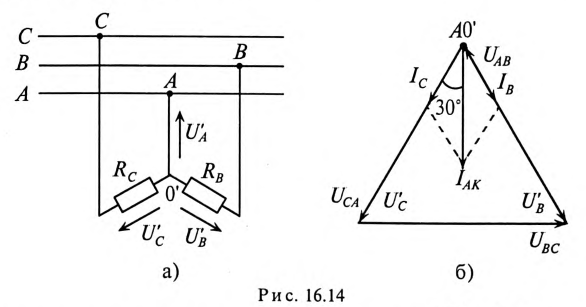
3. При коротком замыкании фазы А схема трехфазной цепи показана на рис. 16.14а, топографическая диаграмма на рис. 16.14б.
Таким образом, точка 0′ на топографической диаграмме при коротком замыкании фазы как бы поднялась в точку А 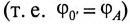
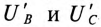
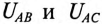
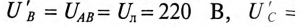
Токи в фазах будут равны 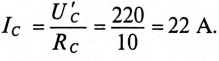
Ток в коротко замкнутой фазе 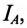
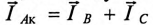
Напряжение 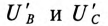
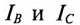
Пример 16.2
К соединенному звездой генератору с фазным напряжением 127 В подключен потребитель, соединенный треугольником. Активное сопротивление каждой фазы потребителя R = 8 Ом, индуктивное 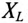
Определить ток в каждой фазе генератора, отдаваемую им мощность и построить векторную диаграмму.
Решение
Эту задачу можно решить, не прибегая к символическому методу и построению топографической диаграммы.
Напряжение на каждой фазе потребителя 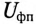
Сопротивление каждой фазы потребителя равно
Ток каждой фазы потребителя (нагрузка равномерная):
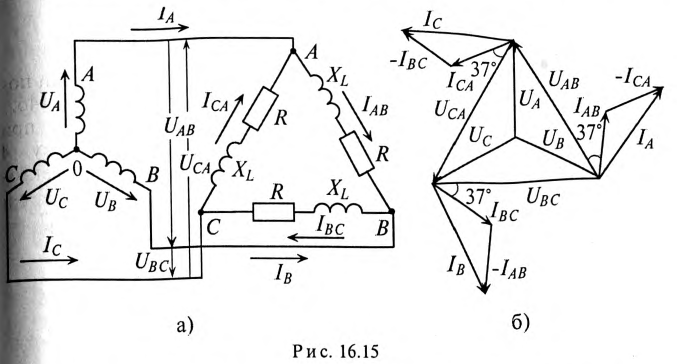
В каждой фазе генератора проходит линейный ток потребителя, единенного треугольником, т.е. (см. рис. 16.15а)
Отдаваемая генератором мощность (активная мощность) равна
Так как
Угол 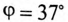
Таким образом, ток фазы потребителя отстает от напряжения на угол 37°, так как нагрузка индуктивного характера.
Вычисленные величины легли в основу построения векторной диаграммы (рис. 16.15б).
Пример 16.3
Параметры трехфазного потребителя, соединенного звездой, имеют следующие значения: 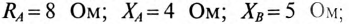
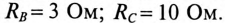
1) напряжение на каждой фазе потребителя;
2) токи каждой фазы потребителя;
3) мощности 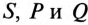
Решение
Допустим, что обмотки генератора соединены звездой, тогда напряжение каждой фазы генератора (при симметричной системе ЭДС)
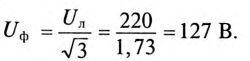
Напряжение на каждой обмотке генератора в комплексной форме:
Сопротивление 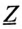
Проводимости 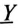
Напряжение смещения нейтрали 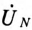
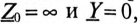
При вычислении 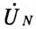
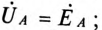
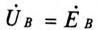
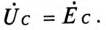
Токи в каждой фазе потребителя: 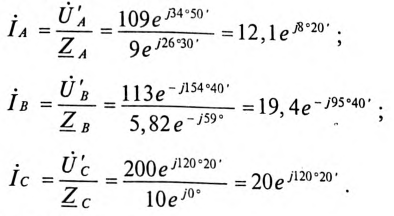
Мощности каждой фазы потребителя:
Мощность всей трехфазной нагрузки:
Векторная диаграмма рассматриваемой цепи изображена на рис. 16.17.
Пример 16.4
К трехфазной сети с линейным напряжением 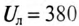
Обмотки трехфазного двигателя мощностью 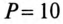
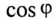
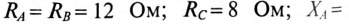
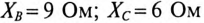
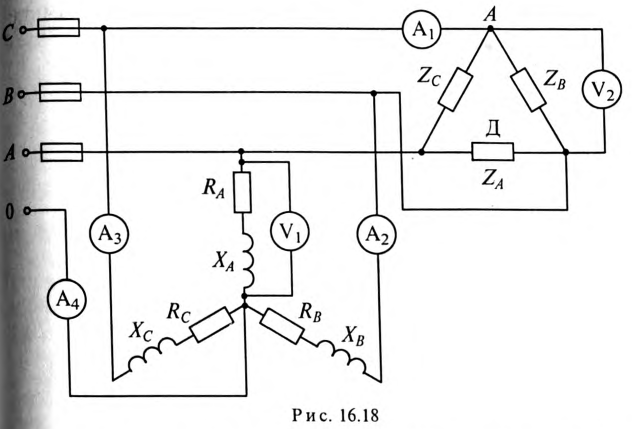
Определить: показания амперметров 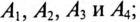
В линейном проводе С сгорел предохранитель (обрыв линейного провода С). Как при этом изменится показание вольтметpa 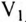
Решение
Расчет трехфазной цепи (рис. 16.18) можно осуществить, не прибегая к символическому методу и построению топографической диаграммы.
Амперметр 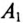
Амперметр 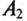
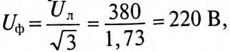
так как
Показания амперметра 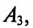
так как
Амперметр 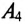
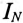
Для вычисления геометрической суммы токов фаз необходимо построить векторную диаграмму токов (рис. 16.19).
При наличии нулевого провода напряжения на фазах сдвинуты на угол 120°. Угол сдвига фаз между током и напряжением, исходя из условий, для всех трех фаз одинаков (это видно из заданных параметров силового потребителя):
Следовательно, фазные токи сдвинуты так же, как и напряжения, на угол 120°. Величины токов определены: 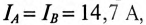
На векторной диаграмме складываются геометрически 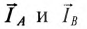
Поскольку этот суммарный ток находится в противофазе с током 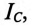
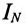
Следовательно, амперметр 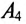
Для расчета мощности Р, потребляемой всей нагрузкой, вычисляется активная мощность каждого силового потребителя:
Тогда активная мощность, потребляемая всей нагрузкой, будет равна
При обрыве линейного провода С и нулевого провода две фазы силового потребителя А и В кажутся соединенными последовательно и подключенными к личному напряжению 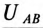
Таким образом, вольтметр 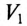
При обрыве линейного провода С фазы В и С двигателя окажутся соединенными последовательно и подключенными к линейному напряжению 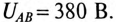
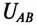
Таким образом, вольтметр 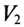
Вращающееся магнитное поле двухфазного тока
Двухфазным током называется совокупность двух однофазных токов, сдвинутых по фазе на угол 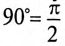
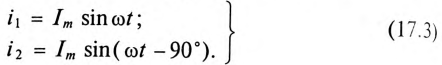
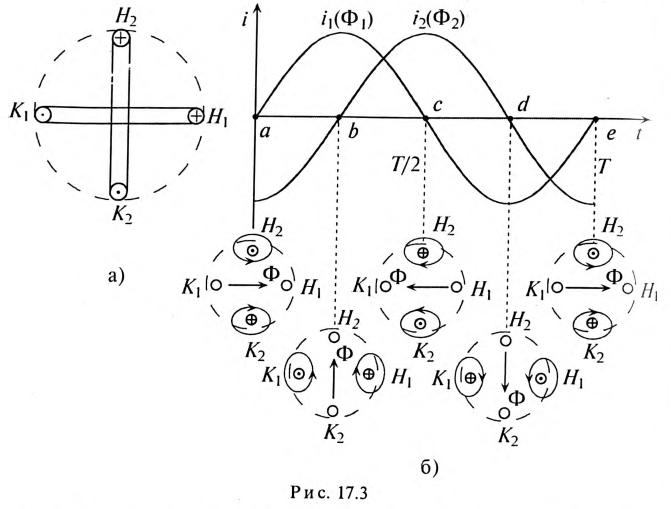
Эти токи создают в обмотках переменные магнитные потоки, сдвинутые по фазе также на угол 90°:
Таким образом, если по двум неподвижно скрепленным под углом 90° обмоткам пропустить двухфазный ток, то внутри этих обмоток (рис. 17.3а) создается вращающееся магнитное поле двухфазного тока.
Как видно (рис. 17.3б), постоянный магнитный поток 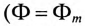
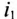
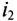
Нетрудно убедиться в том, что если бы второй ток 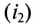
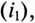
Пульсирующее магнитное поле
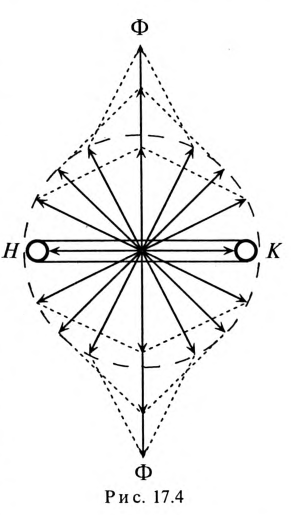
Если по неподвижной катушке (обмотке) машины пропустить синусоидальный ток 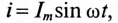
Пульсирующее магнитное поле, к видно из рис. 17.4, можно рассматривать как два магнитных поля, вращающихся в разные стогны. Поэтому в машинах, в которых используется пульсирующее магнитное поле, отсутствует пусковой момент. Для работы таких машин его необходимо создать. Пусковой момент в таких машинах создают или механически, или за счет пусковой обмотки, по которой в момент пуска пропускают импульс тока, сдвинутого по фазе относительно основного синусоидального тока, проходящего по катушке (обмотке) машины (аналогично двухфазному току).
Видео:Трехфазная система. Анимация электрических процессовСкачать

Определение трёхфазных цепей
Наряду с однофазными источниками существуют источники энергии, содержащие две, три, четыре и т.д., характеризуемые тем, что их ЭДС, имея одинаковую частоту, сдвинуты друг относительно друга на некоторый угол. Такие генераторы называются многофазными, а электрические цепи с такими источниками — многофазными.
Трёхфазный генератор
Трёхфазные цепи получили наибольшее практическое применение. В связи с этим основные исследования многофазных цепей будем проводить на примере трёхфазных. Рассмотрим вопрос реализации трёхфазного источника, которым является трёхфазный генератор (рис. 4.1).
Рис. 4.1. Трёхфазный генератор
Для упрощения понимания принципа работы генератора обмотки (фазы) представлены одним витком. В качестве ротора генератора выбран постоянный магнит. Каждая из обмоток имеет начало — клеммы 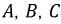
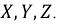
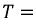
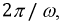
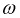
Последовательность, в которой ЭДС достигают максимума в соответствующих фазах, носит название порядка чередования фаз. Прямым порядком чередования фаз называют последовательность 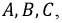
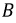
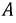
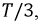
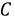
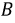
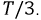
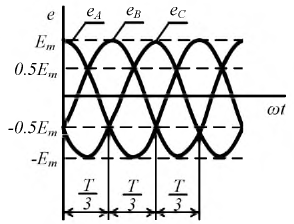
Рис. 4.2. Графики мгновенных значений ЭДС фаз
Запишем мгновенные значения ЭДС, индуктируемые в фазах при вращении ротора генератора:
Поскольку ЭДС каждой фазы генератора синусоидальна, то их можно изобразить на комплексной плоскости в виде векторов соответствующих фазных ЭДС: 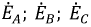
Рис. 4.3. Векторная диаграмма фазных ЭДС
Важным обстоятельством является то, что система векторов фазных ЭДС генератора на комплексной плоскости образует симметричную трехлучевую звезду и сумма этих векторов в любой момент времени равна нулю.
При подключении к каждой из фаз генератора нагрузки по ней будет протекать ток. Таким образом, реализуется трёхфазная система.
Способы соединения фаз генератора и нагрузки
Соединение фаз генератора и нагрузки четырехпроводной звездой:
При соединении фаз генератора звездой все концы или начала соединяют в одну общую точку. На рис. 4.4.а показана несвязанная трёхфазная система, в которой каждая фаза генератора и приемника образует отдельную электрическую цепь и поэтому для связи генератора и приемника требуется 6 проводов.
Рис. 4.4. Соединение звездой а) несвязанная трёхфазная система, b) четырехпроводная звезда
При соединении звездой количество проводов уменьшится до 4-х. Причем провод, соединяющий общие (нейтральные или нулевые) точки фаз генератора 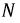
Токи, протекающие по фазам генератора или приемника, называются фазными токами, токи, протекающие по проводам, соединяющим фазы генератора и приемника, — линейными токам, ток, протекающий по нейтральному проводу — нейтральным.
Напряжение между началом и концом фазы генератора или приемника называется фазным, напряжение между двумя фазами или линиями — линейным.
Для этого способа соединения между линейными и фазными параметрами цепи существуют следующие соотношения:
Установим взаимосвязь между комплексами линейных и фазных напряжений источника (рис. 4.5).
Рис. 4.5. Векторно-топографическая диаграмма трёхфазной цепи при соединении приёмников звездой при симметричной активной нагрузке
В дальнейших рассуждениях фазные ЭДС заменим напряжениями на фазах источника:
Выберем любой равнобедренный треугольник, образованный двумя фазными и линейным напряжениями и опустим перпендикуляр из вершины 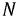
Из любого прямоугольного треугольника получим:
Это второе важное соотношение для соединения звездой.
Частным случаем такого соединения является соединение «звезда-звезда» без нулевого провода.
Соединение фаз генератора и нагрузки треугольником
Вторым базовым способом соединения фаз генератора и нагрузки является соединение типа «треугольник-треугольник» (рис. 4.6).
Рис. 4.6. Соединение «треугольник-треугольник»
При соединении треугольником существует следующее соотношение:
Установим взаимосвязь между фазными и линейными токами:
Построим векторную диаграмму токов и напряжений приемника (рис. 4.7) для данного способа соединения.
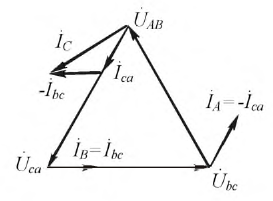
Рис. 4.7. Векторно-топографическая диаграмма трёхфазной цепи при соединении
Рассмотрев любой треугольник токов, можно, аналогично напряжениям при соединении звездой, сделать вывод (только для симметричной нагрузки):
Помимо вышеназванных существуют и комбинированные способы соединения: «звезда-треугольник», «треугольник-звезда».
Режимы работы трёхфазных цепей
Различают симметричный и несимметричный режимы работы трехфазной цепи. При. симметричном режиме сопротивления трех фаз одинаковы и ЭДС образуют трехфазную. симметричную систему. В этом случае токи фаз а, в, с будут равны по величине и сдвинуты по угол 120 градусов.
Соединение «звезда-звезда» с нулевым проводом и без нулевого провода
Поскольку трёхфазные цепи являются совокупностью однофазных цепей, то для их расчета используются все ранее рассмотренные специальные методы, в том числе и комплексный метод расчета. Следовательно, расчет трёхфазных цепей можно иллюстрировать построением векторных диаграмм токов нагрузки и топографических диаграмм напряжений.
Наиболее рациональным методом расчета такой цепи может считаться метод двух узлов. Для выбранных положительных направлений напряжений и токов на схеме (рис. 4.8) составим соответствующую систему уравнений для расчета токов. приемников треугольником и симметричной активной нагрузке
Рис. 4.8. Соединение фаз генератора и приемника по схеме «четырехпроводная звезда»
1. Симметричная нагрузка.
Нагрузка считается симметричной, если комплексные сопротивления ее фаз равны:
Для простоты в качестве потребителей фаз нагрузки будем рассматривать активные сопротивления 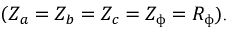
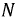
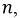
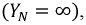
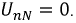
Аналогично для фаз 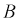
Исходя из сказанного, построим топографическую диаграмму фазных напряжений и векторную диаграмму токов (рис. 4.9).
Рис. 4.9. Векторно-топографическая диаграмма для симметричной нагрузки в трех- и четырехпроводной системах
При симметричной нагрузке, как и в четырехпроводной схеме, фазы приемника работают независимо друг от друга и нулевой провод не нужен. Диаграмма в данном случае будет абсолютно той же, что и для четырехпроводной звезды.
2. Несимметричная нагрузка.
Пусть
На векторно-топографической диаграмме токов и напряжений (рис. 4.10) показано суммирование фазных токов.
Рис. 4.10. Векторно-топографическая диаграмма для несимметричной нагрузки
Пусть 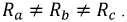
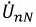
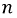
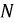
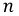
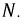
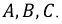
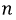
Рис. 4.11. Определение смещения нулевой точки
Соединив точки 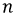
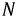
По результатам выполненных построений можно сделать главный вывод: если заведомо известно, что нагрузка несимметрична или может таковою стать, необходимо использовать четырехпроводную схему.
Векторная диаграмма (рис. 4.12) иллюстрирует работу четырехпроводной системы.
Рис. 4.12. Векторно-топографическая диаграмма для обрыва фазы в четырехпроводной системе
Напряжение смещения 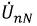
Рис. 4.13. Векторно-топографическая диаграмма для обрыва фазы в трехпроводной системе
По первому закону Кирхгофа:
Поскольку 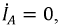
Токи в фазах 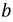
4. Короткое замыкание фазы.
В четырехпроводной системе при коротком замыкании фазы приемника получаем короткое замыкание фазы источника.
Фазные напряжения приемника:
т.е. фазные напряжения увеличились до линейных напряжений, соответственно, токи в фазах:
возросли в 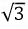
Построение векторно-топографической диаграммы для короткого замыкания показано на рис. 4.14.
5. Разнородная нагрузка.
Общий принцип построения векторных диаграмм токов и топографических диаграмм напряжений остается тем же. Единственное отличие будет состоять в появлении фазовых сдвигов между токами и напряжениями на фазах нагрузки в зависимости от ее характера.
Рис. 4.14. Векторно-топографическая диаграмма для короткого замыкания фазы 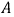
По схеме трехпроводной звезды включают трёхфазные симметричные приемники, например, трёхфазные асинхронные и синхронные двигатели.
Соединение потребителей треугольником
Рассмотрим различные режимы работы приемника при соединении его фаз треугольником (рис. 4.15).
Рис. 4.15. Соединение фаз приемника треугольником
Вновь будем считать, что в качестве потребителей в фазах включены активные сопротивления (для простоты построений).
На рис. 4.7 построена векторная диаграмма для симметричной нагрузки при соединении фаз приемника треугольником.
Токи равны по модулю и отличаются только по фазе:
Фазы по-прежнему работают независимо друг от друга и поэтому токи будут:
Линейные токи определяются соответственно по формулам (4.9). Векторная диаграмма представлена на рис. 4.16.
Рис. 4.16. Векторно-топографическая диаграмма для несимметричной нагрузки приемников, соединенных треугольником
На рис. 4.17 построена векторная диаграмма при соединении приемников треугольником для обрыва фазы.
Рис. 4.17. Векторно-топографическая диаграмма для обрыва фазы при соединении приемников треугольником
Соотношения для токов:
При разнородной нагрузке методика расчета не меняется.
Расчет мощности в трёхфазных цепях
Рассмотрим расчет мощности при соединении приемников по схеме четырехпроводной звезды и допустим, что нагрузка несимметрична. Если учесть, что сопротивление нейтрального провода не равно нулю и активное, имеем:
При симметричной нагрузке для трех- и четырехпроводной системы получим:
При соединении фаз приемника треугольником и несимметричной нагрузке имеем:
При симметричной нагрузке:
При этом необходимо учесть, что одинаковые формулы для расчета мощности при разном способе соединения фаз нагрузки (4.10-4.12) и (4.13- 4.15) не означают одинаковые численные значения.
Пример. Пусть трёхфазный приемник с сопротивлением фазы 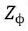
Теперь фазы того же приемника соединим «треугольником» и подключим к тому же трёхфазному источнику:
Измерение мощности в трёхфазных цепях
Для измерения активной мощности в симметричной трехфазной цепи достаточно одного ваттметра, включенного на измерение мощности одной из фаз.
Соединение приемников по схеме четырехпроводной звезды
В схеме (рис. 4.18) однофазные ваттметры включаются в каждую фазу, причем через токовые катушки протекают линейные токи, а катушки напряжения ваттметров включены между нулевым проводом и соответствующими линейными проводами.
Рис. 4.18. Схема включения ваттметров для измерения мощности в четырехпроводной системе
Так как активная мощность — это вещественная часть полной мощности:
то суммарная мощность трех ваттметров может быть представлена выражением:
В случае симметричной нагрузки для измерения мощности, потребляемой ею, достаточно воспользоваться одним ваттметром, показание которого нужно утроить.
Соединение приемников по схеме трехпроводной звезды или треугольником
В этом случае измерить мощность трёхфазного приемника можно с помощью двух ваттметров (рис. 4.19).
Рис. 4.19. Схема измерения активной мощности двумя ваттметрами
Если учесть, что:
Оба ваттметра выполняются в одном корпусе, и прибор имеет две пары выводов для токовых катушек и две пары выводов — для катушек напряжения. Включают трёхфазный ваттметр по приведенной на рис. 4.19 схеме или по любой схеме с циклической заменой фаз.
Метод симметричных составляющих
Любую несимметричную трёхфазную систему можно разложить на три симметричные трёхфазные системы: прямой, обратной и нулевой последовательностей фаз. Такое разложение широко применяется при анализе работы трёхфазных машин и, в особенности, при расчете токов короткого замыкания в трёхфазных системах.
Пусть дана несимметричная трёхфазная система векторов 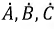
Рис. 4.20. Несимметричная трёхфазная система векторов
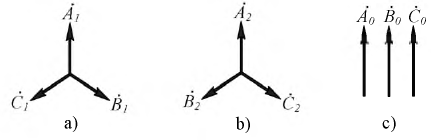
Каждый из векторов этой системы можно представить в виде суммы трех составляющих:
На рис. 4.21 изображены системы указанных выше последовательностей.
Рис. 4.21. Симметричные системы векторов прямой (a), обратной (b) и нулевой (с) последовательностей
Векторы прямой, обратной и нулевой последовательностей подчиняются следующим соотношениям:
где
Коэффициент 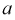
Подставим соотношения (4.19) в систему уравнений (4.18). Тогда получим:
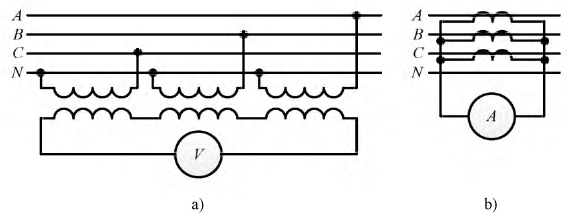
Решение системы уравнений (4.20) относительно 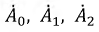
Симметричные составляющие можно определить графически, если на векторной диаграмме несимметричной системы векторов выполнить построения в соответствии с системой уравнений (4.21).
Фильтры симметричных составляющих
Симметричные составляющие несимметричных систем можно определить не только аналитически или графически, но и при помощи электрических схем, называемых фильтрами симметричных составляющих.
Эти фильтры применяются в схемах, защищающих электрические установки. Степень асимметрии системы токов и напряжений не должна превосходить известные пределы, т.е. составляющие нулевой и обратной последовательностей системы напряжений и токов при нормальных режимах должны быть меньше некоторых наперед заданных величин, определяемых для каждой конкретной установки индивидуально.
Возможность выделить при помощи электрических схем отдельные симметричные составляющие позволяет осуществить воздействие любой из них на приборы, защищающие установку, которые, будучи соответствующим образом отрегулированы, отключат или всю установку, или её часть, как только величина соответствующей составляющей превысит допустимый предел.
В качестве примера на рис. 4.22 приведены схемы фильтров нулевой последовательности линейных токов и фазных напряжений.
Рис. 4.22. Схемы фильтров нулевой последовательности
В схеме (рис. 4.22,a) вторичные обмотки трансформаторов напряжения включены последовательно и поэтому вольтметр определяет сумму фазных напряжений, т.е. утроенную составляющую нулевой последовательности системы фазных напряжений.
В схеме (рис. 4.22,b) вторичные обмотки трансформаторов тока включены параллельно и поэтому амперметр измеряет сумму линейных токов, то есть утроенную составляющую нулевой последовательности линейных токов.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока
- Переходные процессы
- Переходные процессы в линейных цепях
- Четырехполюсники
- Линейные диаграммы
- Круговые диаграммы
- Цепи с взаимной индукцией
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Расчет трехфазной цепи при симметричном режимеСкачать

Трехфазные цепи
Содержание:
Общие сведения о трёхфазных цепях
Трёхфазная электрическая цепь может быть представлена как совокупность трёх однофазных цепей, в которой действуют ЭДС одной и той же частоты, сдвинутые относительно друг друга на одну треть периода или, что то же самое, на угол 
Эти три составные части трёхфазной цепи называются фазами и им будем приписывать буквенные обозначения А, В, С. Таким образом, термин «фаза» в электротехнике обозначает два понятия: угол, определяющий стадию периодического процесса, и составную часть трёхфазной цепи.
Изобразим трёхфазную цепь, фазы которой не связаны друг с другом (рис. 1). Такую трёхфазную цепь называют несвязанной (в настоящее время не применяется).
Фазы 


При равенстве амплитуд 


В результате этого достигается экономия материала проводов; кроме того, по сравнению с несвязанной трёхфазной цепью исключаются потери мощности от токов 
Возможно вам будут полезны данные страницы:
Трёхфазная цепь (рис. 3), фазы которой соединены электрически, представляет одну из разновидностей так называемых связанных трёхфазных цепей.
Необходимо отметить, что для получения связанной трёхфазной цепи не требуются отдельные однофазные генераторы, а используется один трёхфазный генератор.
Обмотки трёхфазного генератора могут быть соединены либо звездой, либо треугольником. При соединении звездой концы обмоток соединяют в общую точку, которую называют нейтральной. Начало обмоток обозначают Л, В, С; концы -х, у, z (рис. 4, а).
Начала обмоток соединяют с нагрузкой линейными проводами, по которым идут линейные токи.
Будем в дальнейшем пользоваться следующей терминологией: ЭДС, индуктируемые в обмотках генератора или трансформатора, напряжения на зажимах обмоток и токи в них называть фазными ЭДС, напряжениями и токами, а напряжения между линейными проводами и токи в них — линейными напряжениями и токами. Па схеме (рис. 4, a) 


Связь между линейными и фазными напряжениями устанавливается на основании второго закона Кирхгофа:
Топографическая векторная диаграмма линейных и фазных напряжений генератора приведена на рис. 4, б.
Из векторной диаграммы следует, что при соединении генератора звездой линейные напряжения равны по величине и сдвинуты относительно друг друга на угол 
Па основании геометрических соображений легко показать, что между фазными и линейными напряжениями при соединении звездой существует следующее соотношение:

При соединении генератора треугольником конец первой фазы соединяется с началом второй фазы, конец второй — с началом третьей, конец третьей — с началом первой (рис. 5, а).
Топографическая диаграмма напряжений приведена на рис. 5, я. Векторная диаграмма напряжений показана на рис. 5, б.
Общие точки соединённых обмоток генератора выводятся на зажимы, к которым присоединяются линейные провода или нагрузка.
Нагрузка (потребитель) в трёхфазной цепи также может быть соединена звездой или треугольником.
Симметричный режим работы трёхфазной цепи
Трёхфазные цепи представляют собой разновидность цепей синусоидального тока и поэтому расчёт и исследование их производятся теми же методами, что и для однофазных цепей. Расчёт трёхфазной цепи, так же как и расчёт всякой сложной цепи, ведётся обычно в комплексной форме. Ввиду того что фазные ЭДС и напряжения генератора сдвинуты относительно друг друга на 120°, для краткости математической записи применяется фазовый оператор — комплексная величина:






На рисунке 6, а показано соединение нагрузки звездой. Па схеме обозначены: 

В этой схеме комплексы фазных напряжений источника и комплексы фазных напряжений нагрузки соответствующих фаз равны между собой, т.е.



Соответственно токи в фазах В и С выражаются через ток 
Таким образом, при симметричном режиме работы трёхфазной цепи задача сводится к расчёту одной из фаз аналогичш расчёту однофазной цепи.
Линейное напряжение определяется как разности соответствующих фазных напряжений. Например:
При соединении нагрузки треугольником (рис. 7, а) сопротивления отдельных фаз находятся под линейными напряжениями, поэтому фазные токи в них определяются по закону Ома:
Линейные токи определяются на основании первого закона Кирхгофа. Так, линейный ток фазы А равен
т.е. линейный ток 



Таким образом, при симметричном режиме работы цепи имеет место следующее соотношение:
Векторная диаграмма линейных напряжений и токов при соединении нагрузки треугольником показана на рис. 7, б. Как и при соединении звездой, угол сдвига фаз равен
Активная мощность симметричной трёхфазной цепи равна

Поэтому активная мощность трёхфазной цепи, выраженная через линейные токи и линейные напряжения,
При соединении нагрузки треугольником
Активная мощность трёхфазной цепи будет такой же:
Следовательно, независимо от схемы соединения нагрузки
Аналогично, реактивная мощность
и полная мощность симметричной треугольной цепи
При этом коэффициент мощности определяется из соотношения
где 
Измерение мощности в трёхфазной цепи
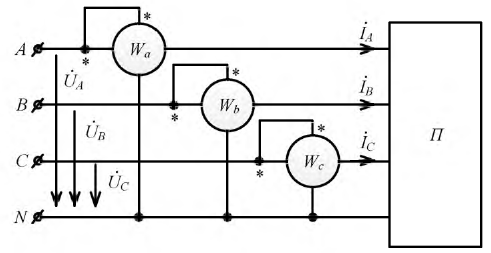
Для измерения мощности в трёхфазной цепи с нейтральным проводом простейшим является метод трёх ваттметров (рис. 12). При таком соединении каждый из ваттметров измеряет активную мощность одной фазы приёмника (нагрузки). Активная мощность всей трёхфазной цепи равна сумме показаний трёх ваттметров:
Если нагрузка симметрична, достаточно произвести измерение одним ваттметром:
При отсутствии нейтрали провода достаточно иметь два ваттметра. В соответствии с (6) для схемы рис. 13 комплекс мощности всей цепи может быть записан как
При выводе формулы (6) не делалось никаких предположений о симметрии цепи; следовательно, данный метод

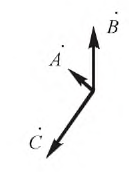
Показания ваттметров следующие:


Измерение реактивной мощности в трёхфазных цепях производится с помощью специальных измерителей реактивной мощности, подобных по устройству ваттметрам. В симметричной трёхфазной цепи измерение реактивной мощности может быть произведено, кроме того, с помощью ваттметров активной мощности. В этом случае ваттметр может быть включён в схему, как показано на рис. 14.
Поскольку при симметричной нагрузке как при соединении треугольником, так и при соединении звездой угол между линейным напряжением 


Для получения суммарной реактивной мощности показание ваттметра нужно умножить на 



На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).
Услуги:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
📸 Видео
Трехфазные цепи - ТРЕУГОЛЬНИК. Расчет трехфазной цепи, соединенной треугольникомСкачать
Расчет трехфазной цепи │ЗВЕЗДА С НУЛЕВЫМ ПРОВОДОМСкачать

Расчет Трехфазной цепи Без комплексных чисел. Соединение треугольникомСкачать

Симметричная нагрузка в трехфазной цепиСкачать

Лекция 060-1. Трехфазные электрические цепи. Основные понятияСкачать

Расчет трехфазной цепи Несинусоидального токаСкачать

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

ТОЭ - Расчет трехфазной цепи с лампами. Найти фазные токи и мощностиСкачать

Расчет трехфазной цепиСкачать

Трехфазные электрические цепи │Теория ч. 2Скачать

Основы электротехники. 07. Трёхфазные цепиСкачать

7. Решение задачи на трехфазные цепи по схеме треугольника.Скачать

Обрыв Фазы. Расчет трехфазной цепи - Звезда без нейтрального проводаСкачать

Расчет трехфазных электрических цепей треугольникСкачать














 ;
;  ;
;  ;
;  . Линейное напряжение равно 380 В.
. Линейное напряжение равно 380 В.
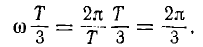
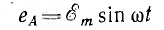
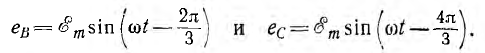
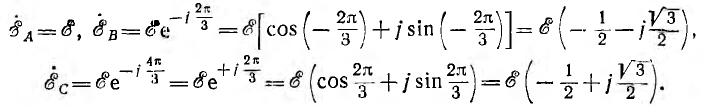
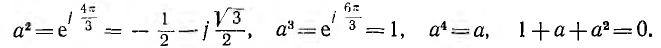
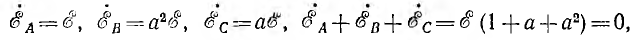
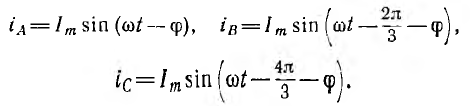
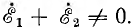
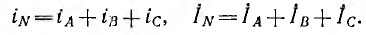
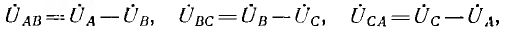
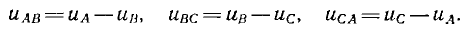
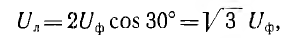
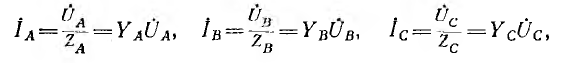
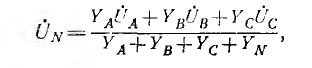
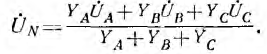
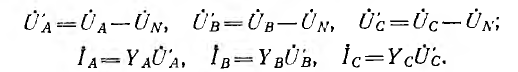
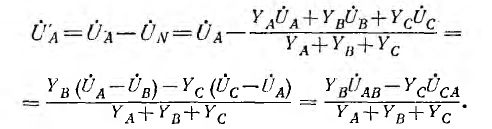
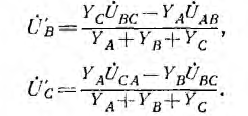
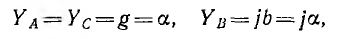
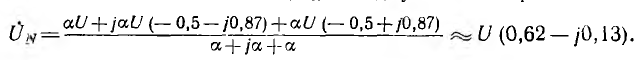
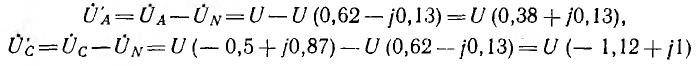
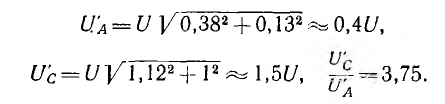
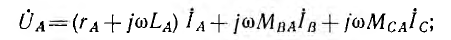
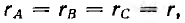
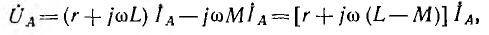
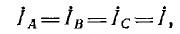
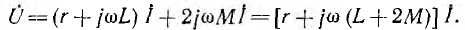
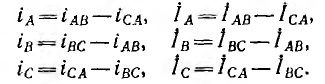
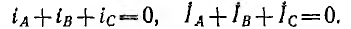
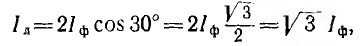
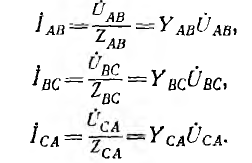
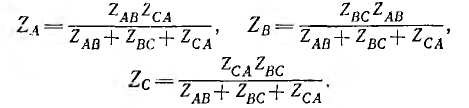
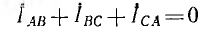
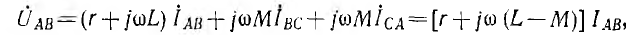
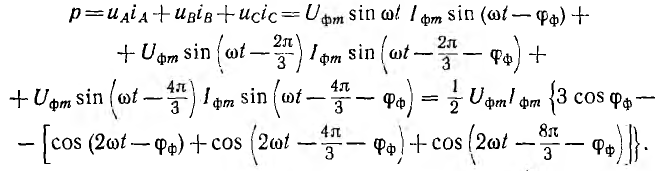
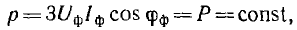
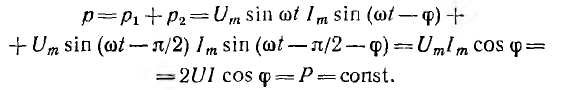
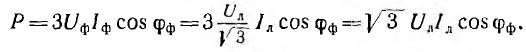
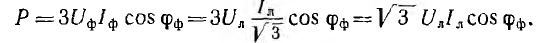
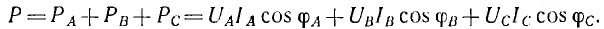
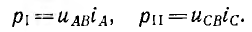
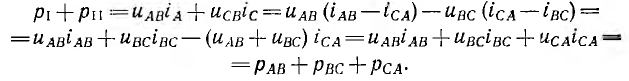
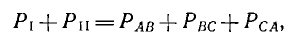
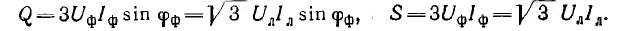
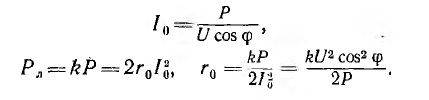
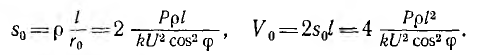
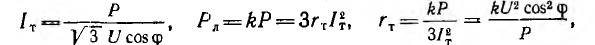
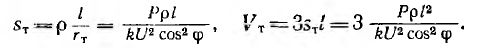
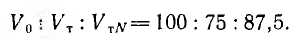
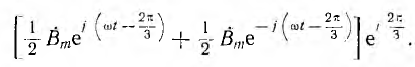
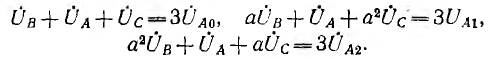
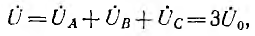
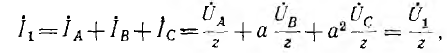
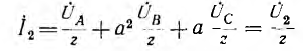
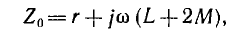
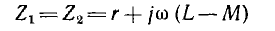
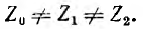
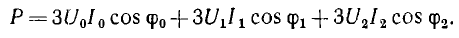
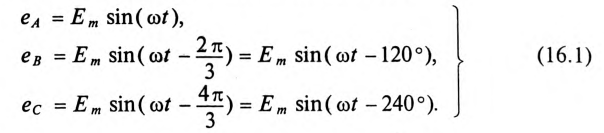
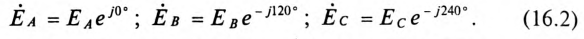
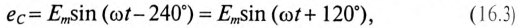

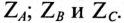
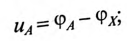
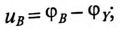
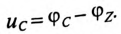
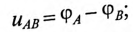
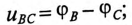
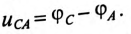
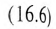

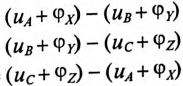
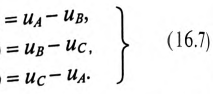
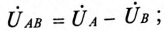
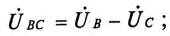
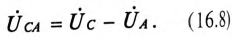
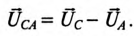
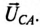
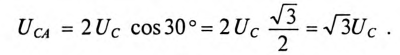


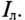
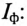

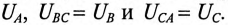

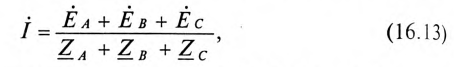
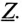
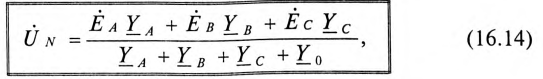
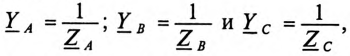
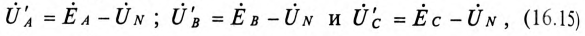


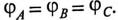
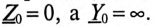
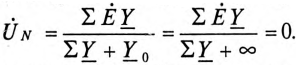


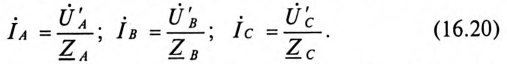
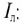

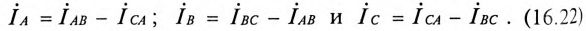
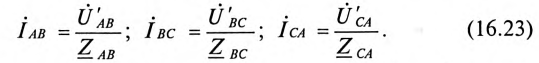

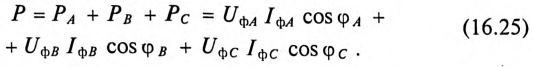
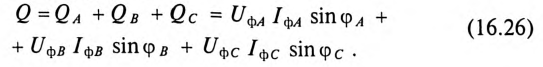
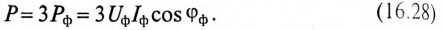
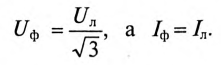
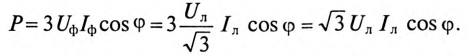
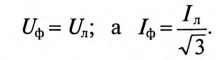
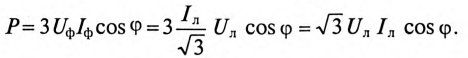


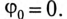
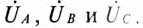
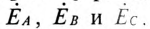
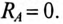
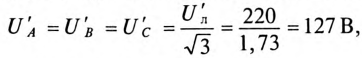
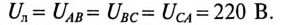
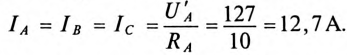
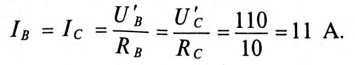
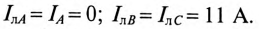
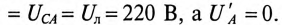
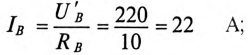
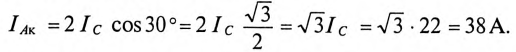
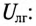
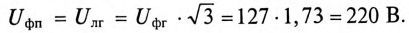
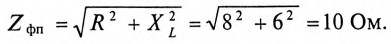
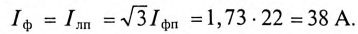
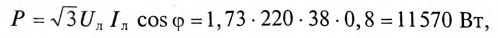
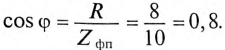
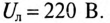
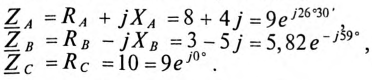
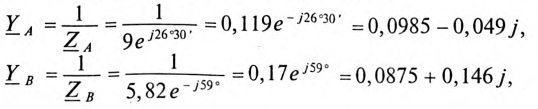
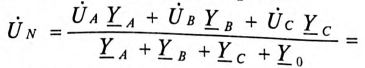
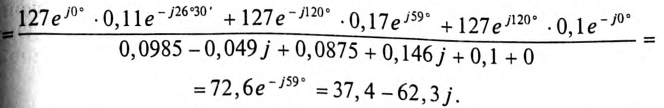
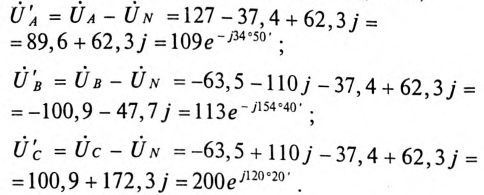
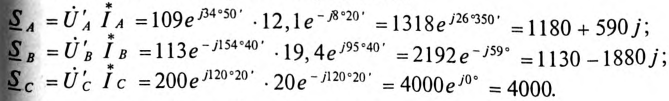
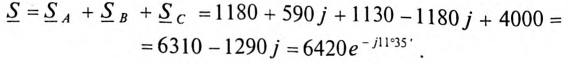
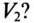
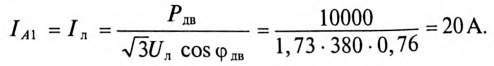
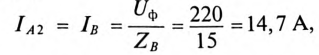
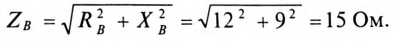
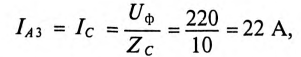
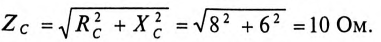
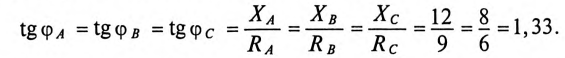
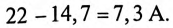
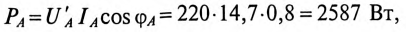
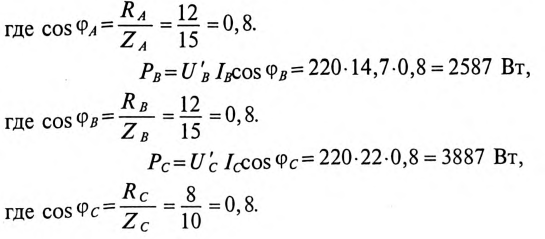
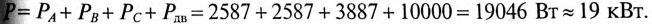
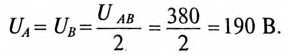
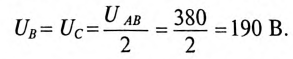
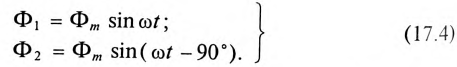
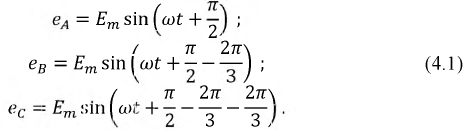

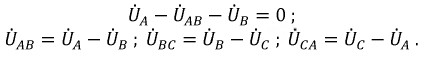
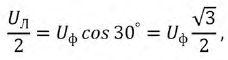


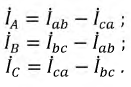

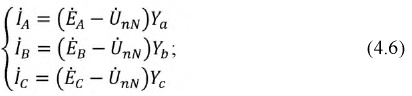
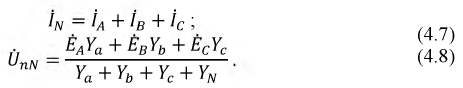
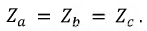
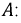
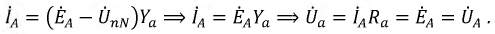
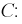
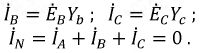
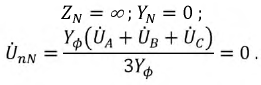
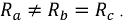
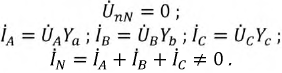
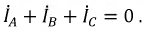
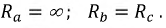
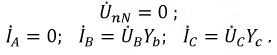
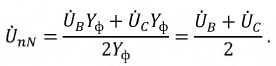
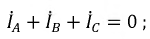
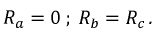
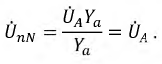
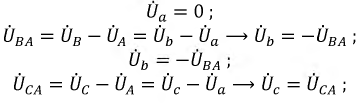
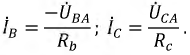
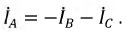
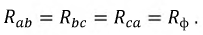
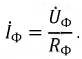

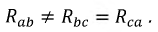
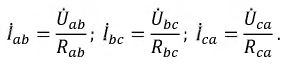
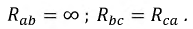
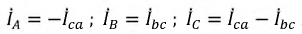
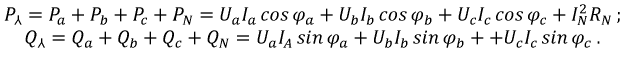
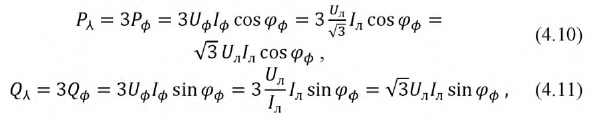
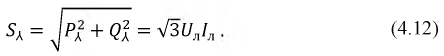
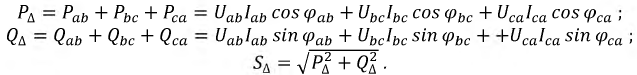
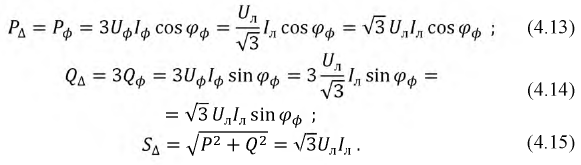
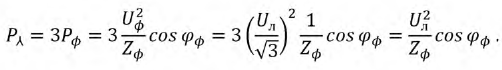
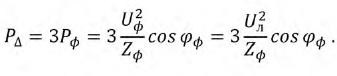
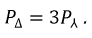
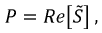
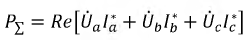
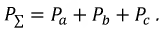
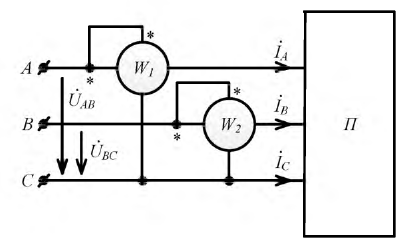
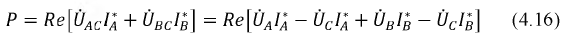
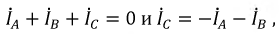
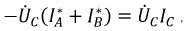
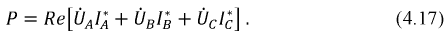
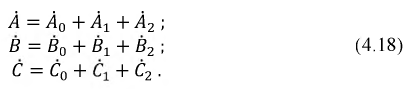
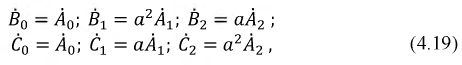
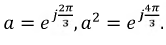
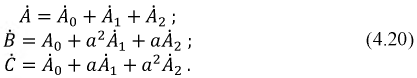
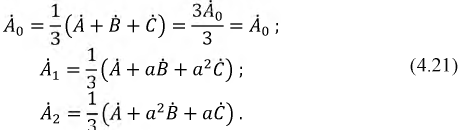
























 При выводе формулы (6) не делалось никаких предположений о симметрии цепи; следовательно, данный метод
При выводе формулы (6) не делалось никаких предположений о симметрии цепи; следовательно, данный метод


