Методы решения систем уравнений с двумя переменными
- Выражаем из какого-либо уравнения системы одну переменную через другую.
- Подставляем вместо этой переменной полученное выражение во второе уравнение.
- Решаем получившееся уравнение с одной переменной.
- Находим соответствующие значения второй переменной.
- Просмотр содержимого документа «Методы решения уравнений, неравенств и их систем»
- Показательные уравнения и неравенства с примерами решения
- Решении показательных уравнений
- Показательные уравнения и их системы
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Системы простейших показательных уравнений
- Пример №7
- Пример №8
- Пример №9
- Приближенное решение уравнений
- Пример №10
- Нахождение приближенного корня с заданной точностью
- Пример №11
- Алгебра. Урок 8. Неравенства, системы неравенств.
- Неравенства
- 📺 Видео
Просмотр содержимого документа
«Методы решения уравнений, неравенств и их систем»
Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики. Однако решению всех видов уравнений и неравенств уделяется недостаточно внимания. Актуальность рассмотрения данной темы обусловлена противоречием между тем, что задания, связанные с уравнениями и неравенствами и их системами регулярно встречаются в материалах ЕГЭ и ОГЭ и тем, что их решение, вызывают у учащихся значительные трудности.
Целью данной работы является: Рассмотреть методические основы профильного и углубленного обучения теме «Уравнения, неравенства и их системы».
Из данной цели вытекают задачи:
Выделить методы решения уравнений, неравенств и их систем.
Выполнить логико-дидактический анализ темы «Уравнения, неравенства и их системы» по школьным учебникам «Алгебра» Ю.Н. Макарычева за 7-9 класс и «Алгебра» А.Г. Мордковича 10-11 класс.
Разработать конспект урока по теме «Уравнения, неравенства и их системы» для 8 класса.
Данные практические разработки могут быть использованы в школе.
Данная работа состоит из трех параграфов:
§1. Методы решения уравнений, неравенств и их систем.
§2. Логико-дидактический анализ по теме «Уравнения, неравенства и их системы» по школьным учебникам «Алгебра» Ю.Н. Макарычева за 7-9 класс и «Алгебра» А.Г. Мордковича 10-11 класс.
§3. Конспект урока по теме «Уравнения, неравенства и их системы» для 8 класса.
§1. Методы решения уравнений, неравенств и их систем
Методы решения целых уравнений первой степени.
Раскрытие скобок (умножаем многочлен на многочлен). Пример: (2x+1)(3x-2)-6x(x+4)=67-2x
Домножение на НОК знаменателей дробей обеих частей уравнения. Пример: 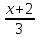
Способы решения целых уравнений.
Разложение многочлена на множители. Пример: 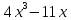
С помощью теоремы о корне многочлена. Пример:
Введение новой переменной. Пример:
Метод неопределенных коэффициентов. Пример:
Графический способ. Пример:
С помощью алгоритма решения квадратных уравнений:
Алгоритмы и способы решения дробно-рациональных уравнений.
а) Умножаем обе части уравнения на общий знаменатель дробей, входящих в уравнение.
б) Решаем полученное целое уравнение.
в) Исключаем из его корней те, которые обращают в нуль общий знаменатель дробей.
Пример:
Используя нестандартные преобразования. Пример:
Введение новой переменной. Пример:
Введение вспомогательной переменной. Пример:
Графический способ решения. Пример:
Способы решения целых неравенств с одной переменной.
1.Используя свойства дискриминанта квадратного уравнения и свойств графика квадратичной функции. Пример:
2. Метод интервалов. Пример:
3. Используя свойства графика квадратной функции. Пример:
Способы решения дробно-рациональных неравенств с одной переменной.
Разложение на множители числителя и знаменателя. Пример:
Используя систему. Примеры:
Способы решения уравнений с переменной под знаком модуля.
Замена на систему уравнений. Пример:
Замена совокупность из двух систем. Пример:
Графический способ с дальнейшей заменой на совокупность из трех систем уравнений. Пример:
Способы решения неравенств с переменной под знаком модуля.
Замена на систему неравенств. Пример:
Используя свойство модуля. Пример:
Графический способ с дальнейшей заменой на совокупность из трех систем неравенств. Пример:
Способы решения уравнений с параметром.
Вынесение многочлена за скобку. Пример: ax-2x=a 2 +a-6
Используя дискриминант. Пример:
Способы решения дробно-рациональных уравнений с параметром.
Домножение на общий знаменатель. Пример:
Методы решения систем уравнений с двумя переменными
Выражаем из какого-либо уравнения системы одну переменную через другую.
Подставляем вместо этой переменной полученное выражение во второе уравнение.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Умножаем левые и правые части уравнений.
Складываем почленно левые и правые части уравнений.
Решаем получившееся при сложении уравнение с одной переменной.
Находим соответствующие значения второй переменной.
б) Разложение на линейные множители.
Способы решения линейных неравенств с двумя переменными.
Графический. Пример: 4x-5y20
Способы решения неравенств с двумя переменными выше первой.
Способы решения системы неравенств с двумя переменными.
Способы решения неравенств с двумя переменными, содержащие знак модуля.
Методы решения уравнений высших степеней.
Используя делители свободного члена уравнения. Пример: x 3 +2x 2 -7x-12=0
Деления обеих частей уравнения на x 2 . Пример: 3x 4 -2x 3 -9x 2 -4x+12=0
Метод замены двух переменных. Пример: 2(x 2 +x+1)-7(x-1) 2 =13(x 3 -1)
Графический метод. Пример: x 5 +5x-42=0
Используя производную функции. Пример: x 4 -8x+63=0
Методы решения показательных уравнений.
Метод введения новой переменной. Пример: 4 x +2 x +1 -24=0
Методы решения показательных неравенств.
Метод уравнивания показателей. Пример:
Метод введения новой переменной. Пример:
Деления обеих частей уравнения на число с наибольшим показателем в степени. (однородные уравнения второй степени) Пример: 8 x +18 x 2∙27 x
Используя свойство дискриминанта. Пример: (x 2 +x+1) x ≤1
Методы решения логарифмических уравнений.
Введение новой переменной. Пример: lg 2 x+lg x+1=
Методы решения логарифмических неравенств.
Представление обеих частей неравенства в виде логарифмов с одинаковым основанием. Пример: (16+4x—x 2 )≤-4
Введение новой переменной. Пример:
Методы решения уравнений и неравенств с модулем.
Раскрытие модуля по определению. Пример:
Графический способ. Пример:
Используя совокупность уравнений (неравенств). Пример:
Методы решения иррациональных уравнений.
Возведение обеих частей уравнения в одну и ту же степень. Пример:
Введение новой переменной. Пример:
Уединение корня и возведение обеих частей уравнения в степень. Пример:
Введение двух новых переменных. Пример:
Умножение обеих частей уравнения на выражение сопряженное данному. Пример:
Методы решения иррациональных неравенств.
Используя совокупность неравенств. Пример:
Введение новой переменной. Пример:
Методы решения систем уравнений.
Перемножением правых и левых частей уравнения. Пример:
Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Алгебра. Урок 8. Неравенства, системы неравенств.
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Неравенства
- Линейные неравенства
Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
≥ больше или равно,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой .
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной .
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x c | x ∈ ( − ∞ ; c ) | |
| x ≤ c | x ∈ ( − ∞ ; c ] | |
| x > c | x ∈ ( c ; + ∞ ) | |
| x ≥ c | Алгоритм решения линейного неравенства
a x b a x ≤ b a x > b a x ≥ b
Примеры решения линейных неравенств: №1. Решить неравенство 3 ( 2 − x ) > 18. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. − 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 ) Делим обе части неравенства на ( -3 ) – коэффициент, который стоит перед x . Так как − 3 0 , знак неравенства поменяется на противоположный . x 12 − 3 ⇒ x − 4 Остается записать ответ (см. таблицу числовых промежутков). Ответ: x ∈ ( − ∞ ; − 4 ) №2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x + 4 ≥ 3 x + 3 − 14 6 x − 3 x ≥ 3 − 14 − 4 3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на ( 3 ) – коэффициент, который стоит перед x . Так как 3 > 0, знак неравенства после деления меняться не будет. x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков). Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно). №1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x − 6 x ≤ − 1 + 1 Получили верное неравенство, которое не зависит от переменной x . Возникает вопрос, какие значения может принимать переменная x , чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа. Ответ:
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. x + 6 − 9 x > − 8 x + 48 − 8 x + 8 x > 48 − 6 Получили неверное равенство, которое не зависит от переменной x . Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ. Квадратные неравенства Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная. Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет. Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4). Алгоритм решения квадратного неравенства методом интервалов
Если знак неравенства строгий > , , точки будут выколотые. Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий. Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий.
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +. Если знак неравенства или ≤ в ответ выбираем интервалы со знаком -. Примеры решения квадратных неравенств: №1. Решить неравенство x 2 ≥ x + 12. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 1, c = − 12 D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6 . Подставляем эту точку в исходное выражение: x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0 Это значит, что знак на интервале, в котором лежит точка 6 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ . Точки -3 и 4 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ ) №2. Решить неравенство − 3 x − 2 ≥ x 2 . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = − 2 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1 x 1 = − 2, x 2 = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение: − x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0 Это значит, что знак на интервале, в котором лежит точка 0 будет − . Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +. Точки -2 и -1 будут в квадратных скобках, так как они жирные. Ответ: x ∈ [ − 2 ; − 1 ] №3. Решить неравенство 4 x 2 + 3 x . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = 4 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение: − x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0 Это значит, что знак на интервале, в котором лежит точка 2 , будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервалы со знаком − . Точки -4 и 1 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ ) №4. Решить неравенство x 2 − 5 x 6. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 5, c = − 6 D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение: x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0 Это значит, что знак на интервале, в котором лежит точка 10 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком -. Точки -1 и 6 будут в круглых скобках, так как они выколотые Ответ: x ∈ ( − 1 ; 6 ) №5. Решить неравенство x 2 4. Решение: Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения. ( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3 . Подставляем эту точку в исходное выражение: x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0 Это значит, что знак на интервале, в котором лежит точка 3 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком − . Точки -2 и 2 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 2 ; 2 ) №6. Решить неравенство x 2 + x ≥ 0. Решение: Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0. x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1 . Подставляем эту точку в исходное выражение: x 2 + x = 1 2 + 1 = 2 > 0 Это значит, что знак на интервале, в котором лежит точка 1 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ ) Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже. Дробно рациональные неравенства Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов: f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0 Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю). Примеры дробно рациональных неравенств: x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3 Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов. Алгоритм решения дробно рациональных неравенств:
f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
Вне зависимости от знака неравенства Если знак неравенства строгий , Если знак неравенства нестрогий ,
Примеры решения дробно рациональных неравенств: №1. Решить неравенство x − 1 x + 3 > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
x = 1 — это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
x = − 3 — это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства) .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0, Это значит, что знак на интервале, в котором лежит точка 2 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые. Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ ) №2. Решить неравенство 3 ( x + 8 ) ≤ 5. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
3 ( x + 8 ) − 5 x + 8 ≤ 0 3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 x − 40 x + 8 ≤ 0 − 5 x − 37 x + 8 ≤ 0
x = − 37 5 = − 37 5 = − 7,4 x = − 7,4 — ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
x = − 8 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : − 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0 Это значит, что знак на интервале, в котором лежит точка 0 будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -. В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная. Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ ) №3. Решить неравенство x 2 − 1 x > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1 x 1 = 1, x 2 = − 1 — нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
x = 0 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ ) Системы неравенств Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой. Пример системы неравенств: Алгоритм решения системы неравенств
Примеры решений систем неравенств: №1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 4 на графике жирная, так как знак неравенства нестрогий.
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный. Графическая интерпретация решения: Точка 2 на графике жирная, так как знак неравенства нестрогий.
Пересечение решений наблюдается на отрезке от 2 до 4 . Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные. №2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 3 на графике жирная, так как знак неравенства нестрогий.
3 x − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения: Точка -1 на графике выколотая, так как знак неравенства строгий.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая. Ответ: x ∈ ( − ∞ ; − 1 ) №3. Решить систему неравенств 5 − x Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения:
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения:
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений. №4. Решить систему неравенств 0 2 x + 3 ≤ x 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения первого неравенства:
Решаем методом интервалов. a = − 1, b = 2, c = 3 D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16 D > 0 — два различных действительных корня. x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1 Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными. Графическая интерпретация решения второго неравенства:
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ . Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные. 📺 ВидеоКак решать неравенства? Математика 10 класс | TutorOnlineСкачать  Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать  Как решать неравенства? Часть 1| МатематикаСкачать  Решение системы неравенствСкачать  Решение неравенства методом интерваловСкачать  ПРОСТЕЙШИЙ метод решения систем квадратных неравенствСкачать  Иррациональные уравнения и их системы. 11 класс.Скачать  Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать  Решение системы неравенств с двумя переменными. 9 класс.Скачать  ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать  Как решить неравенства с модулем?Скачать  Нестандартные методы решения уравнений, неравенств, систем. (часть 1).Скачать  Решение систем уравнений методом подстановкиСкачать  СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать  Решение системы линейных уравнений графическим методом. 7 класс.Скачать  Решение квадратных неравенств методом интервалов. 8 класс.Скачать  |

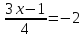
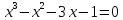
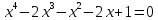
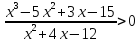
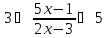
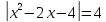
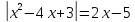
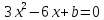










































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);












