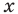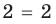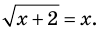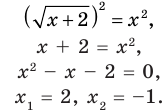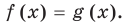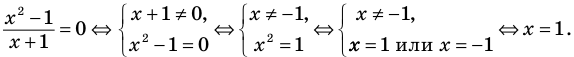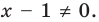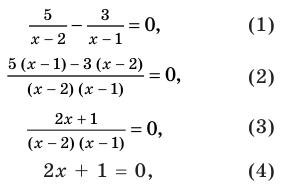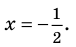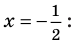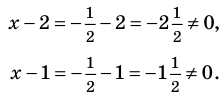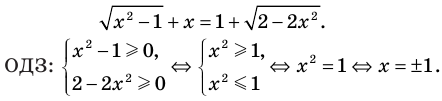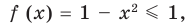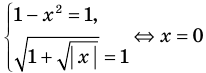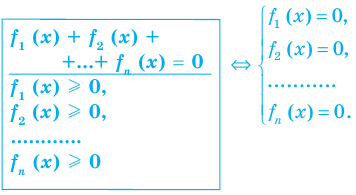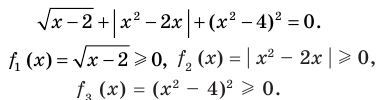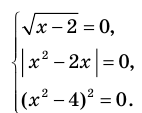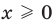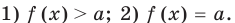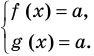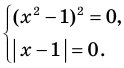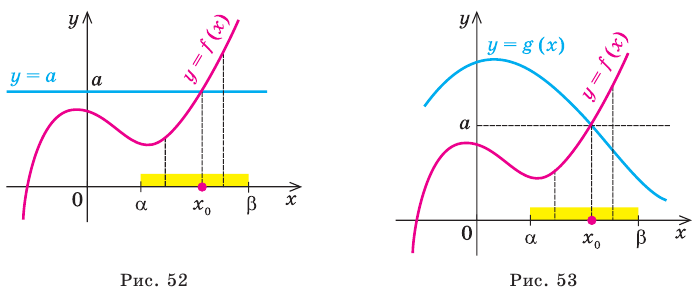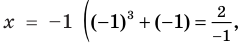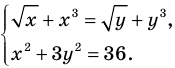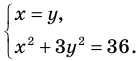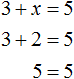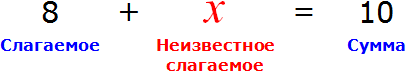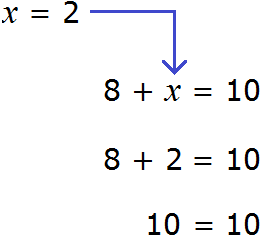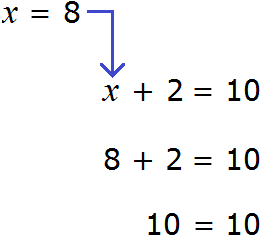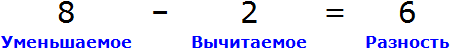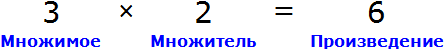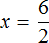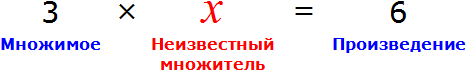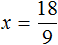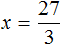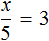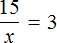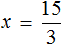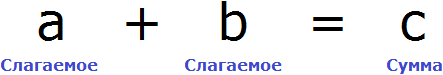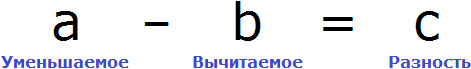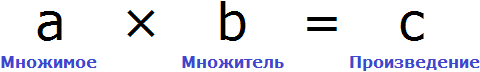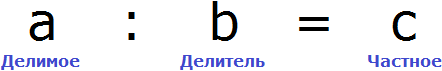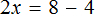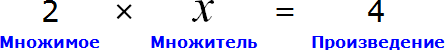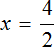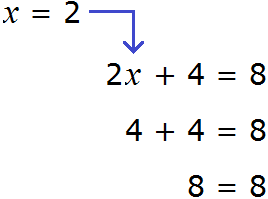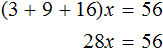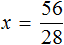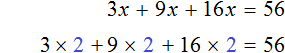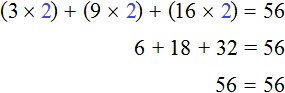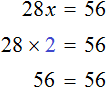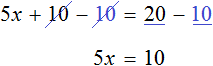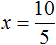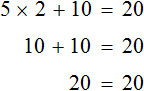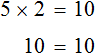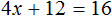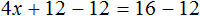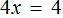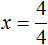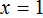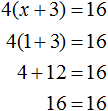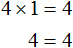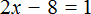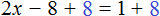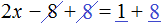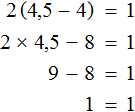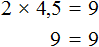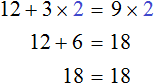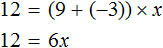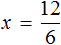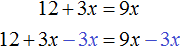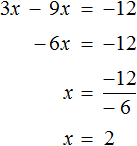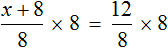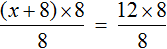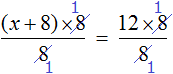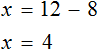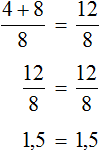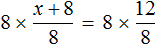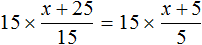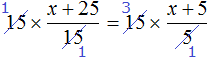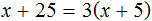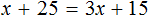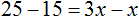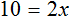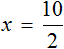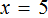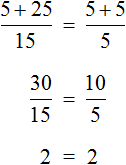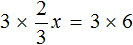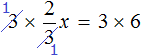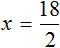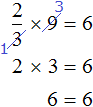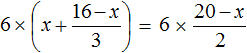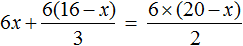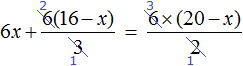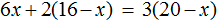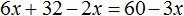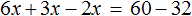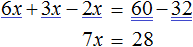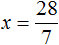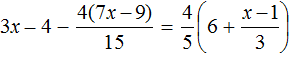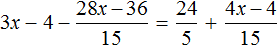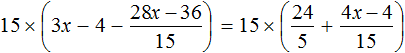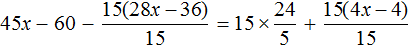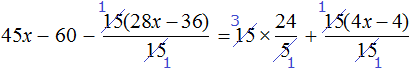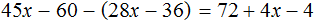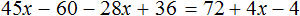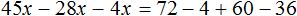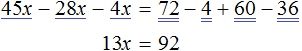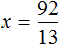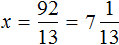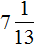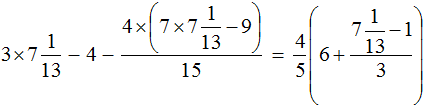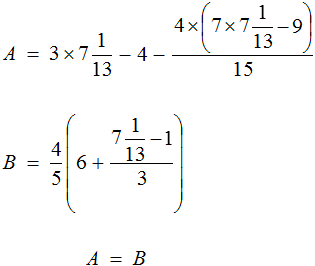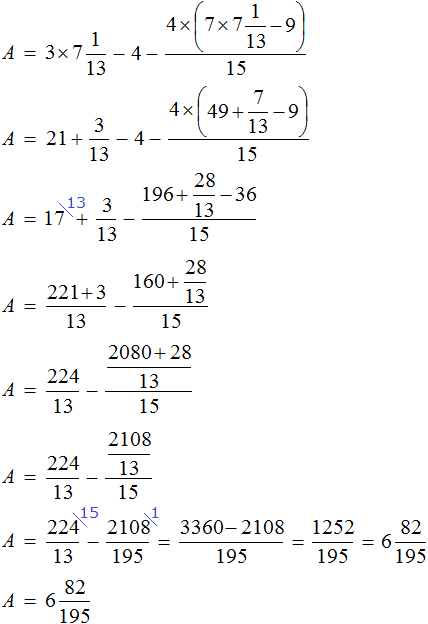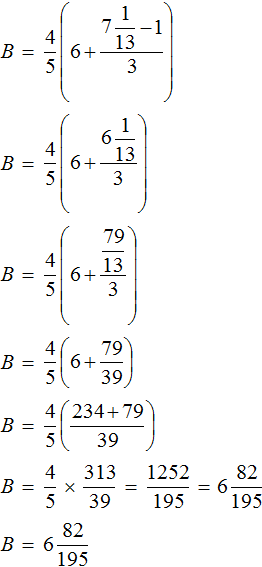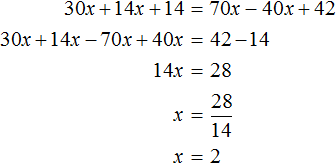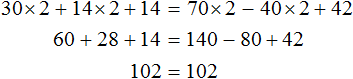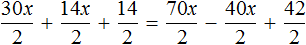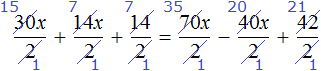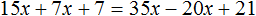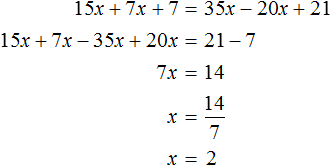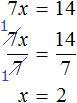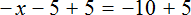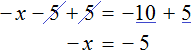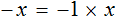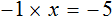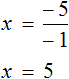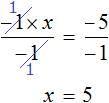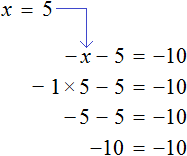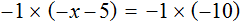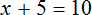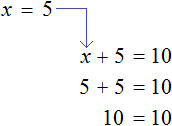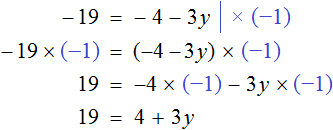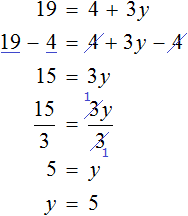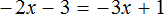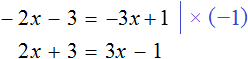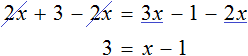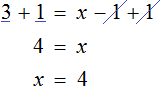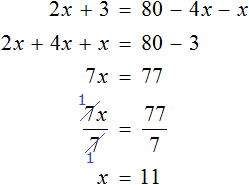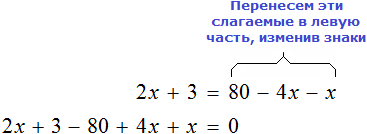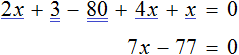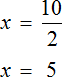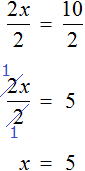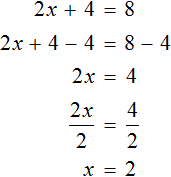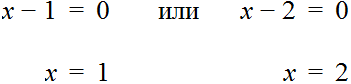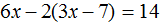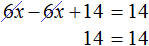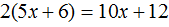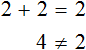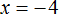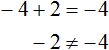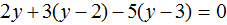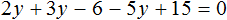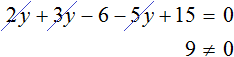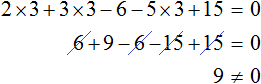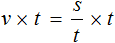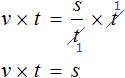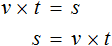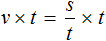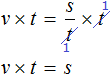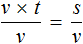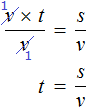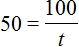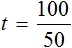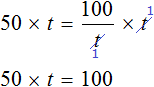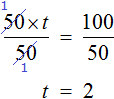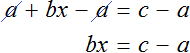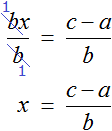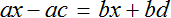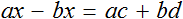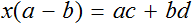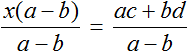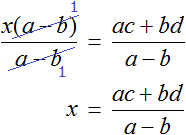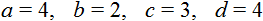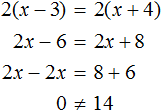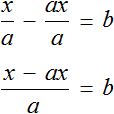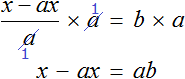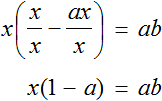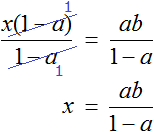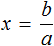После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
- Понятие уравнения
- Корень уравнения
- Уравнение — определение и вычисление с примерами решения
- Уравнения
- Уравнения-следствия и равносильные преобразования уравнений
- Понятие уравнения и его корней
- Область допустимых значений (ОДЗ) уравнения
- Методы решения уравнений
- Уравнения-следствия
- Равносильные уравнения
- Причины появления посторонних корней и потери корней при решении уравнений
- Применение свойств функций к решению уравнений
- Конечная ОДЗ
- Оценка левой и правой частей уравнения
- Использование возрастания и убывания функций к решению уравнений
- Общие сведения об уравнениях
- Что такое уравнение?
- Выразить одно через другое
- Правила нахождения неизвестных
- Компоненты
- Равносильные уравнения
- Умножение на минус единицу
- Приравнивание к нулю
- Альтернатива правилам нахождения неизвестных
- Когда корней несколько
- Когда корней бесконечно много
- Когда корней нет
- Буквенные уравнения
- Линейные уравнения с одним неизвестным
Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня — 2 , 1 и 5 , то пишем — 2 , 1 , 5 или .
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Уравнение — определение и вычисление с примерами решения
Содержание:
Видео:Квадратные уравнения. Основные понятия | Алгебра 8 класс #33 | ИнфоурокСкачать

Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
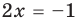
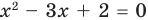
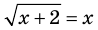
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
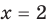
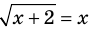
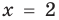
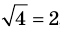
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 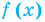
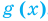
Для уравнения 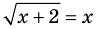
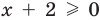
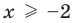
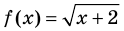

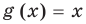
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
Решение:
► Возведем обе части уравнения в квадрат:
Проверка, 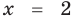
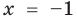
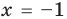
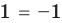
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
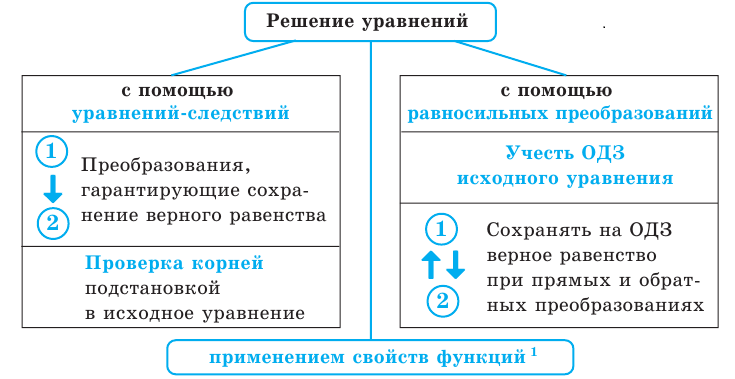
5. Схема поиска плана решения уравнений



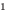
Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 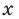
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 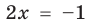
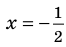
а уравнение 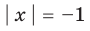
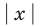
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 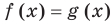
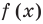
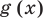
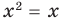
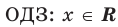
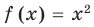
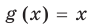
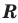
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 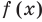
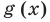
Например, в уравнении 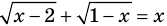
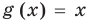
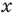
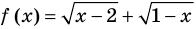
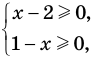
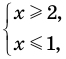
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 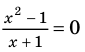
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 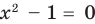
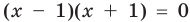
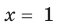
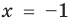
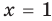
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
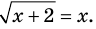
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
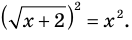
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 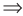
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 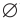
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 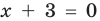
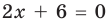
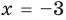
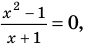
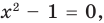
то, как было показано выше, уравнение (3) имеет единственный корень 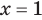
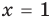
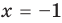
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 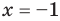
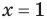
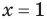
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 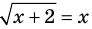
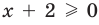

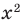
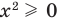
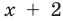


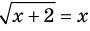
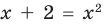
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 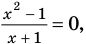
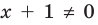
Запись решения в этом случае может быть такой:
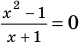
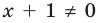
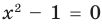
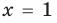
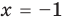
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок 
Пример №423
Решите уравнение 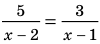
Решение:
► ОДЗ: 
На этой ОДЗ данное уравнение равносильно уравнениям:
то есть
Учтем ОДЗ. При
Таким образом, 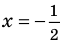
Ответ:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
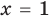
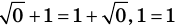
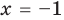
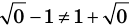
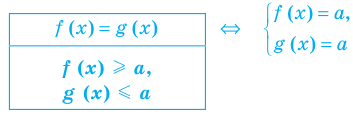
2. Оценка левой и правой частей уравнения
Если надо решить уравнение вида 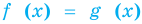


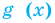
Пример:
►
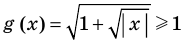
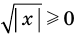
Итак, заданное уравнение равносильно системе
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►
Итак, заданное уравнение равносильно системе
Из первого уравнения получаем 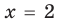
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
Теоремы о корнях уравнения
Если в уравнении 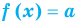
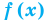
Пример:
Уравнение 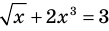
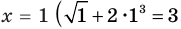
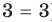
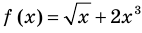
Если в уравнении 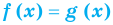
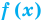
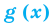
Пример:
Уравнение 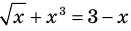
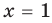
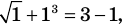
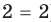
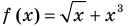

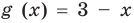
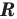
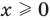
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 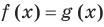
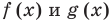
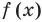
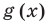
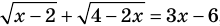
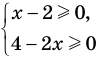
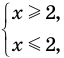


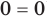


Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 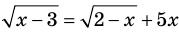
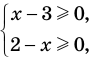
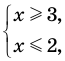
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 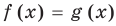
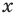
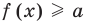
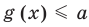
Рассмотрим два случая:
Если 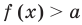
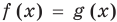
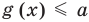
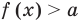
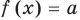
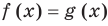
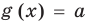
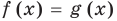
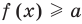
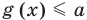
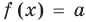
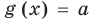
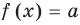
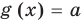
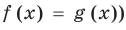
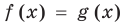
Коротко это можно записать так:
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 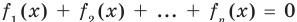
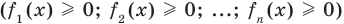
Если предположить, что 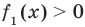

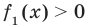
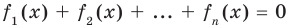
Например, чтобы решить уравнение 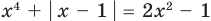
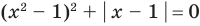
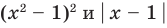
Из второго уравнения получаем 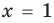
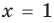
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
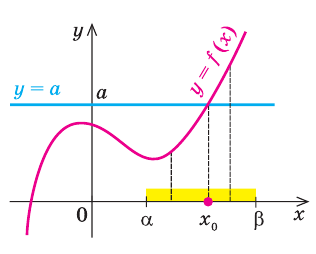
Теорема 1. Если в уравнении 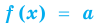
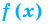
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 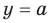
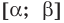
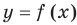
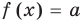
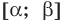
• Если на промежутке 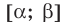
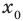
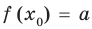
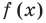
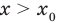
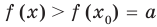
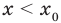
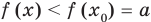
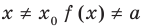
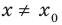
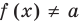
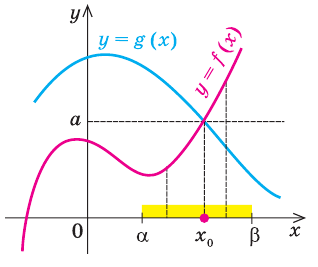
Теорема 2. Если в уравнении 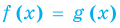
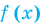
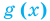
Графически утверждение теоремы проиллюстрировано на рисунке 53.
• Если на промежутке 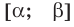
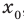
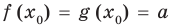
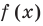
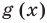
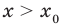
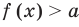
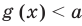
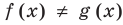
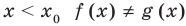
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 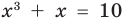
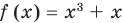

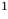
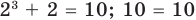
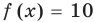
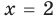
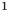

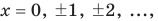
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 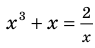
► Сначала следует учесть его ОДЗ: 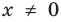
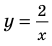
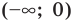
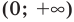
1) При 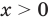
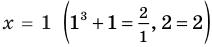
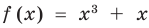

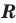
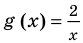

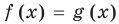
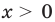
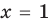
2) При 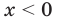
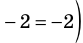
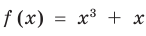
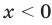
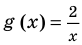
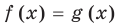
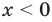
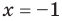
Примеры решения задач:
Пример №424
Решите уравнение 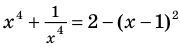
Решение:
► ОДЗ: 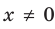
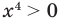
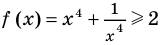
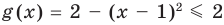
Таким образом, данное уравнение равносильно системе 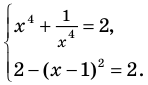


Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 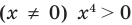
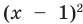
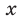
Пример №425
Решите систему уравнений
Решение:
► ОДЗ: 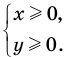
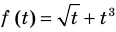
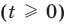
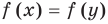
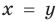
Подставляя 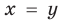
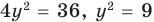
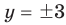

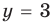
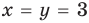
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 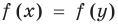
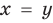
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 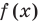
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Общие сведения об уравнениях
Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.
С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Что такое уравнение?
Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.
Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5 .
А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x , значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.
Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет
Говорят, что число 2 является корнем или решением уравнения 3 + x = 5
Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.
Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.
Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.
Видео:8 класс, 24 урок, Основные понятия, связанные с квадратными уравнениямиСкачать

Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение:
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
Мы выразили число 2 из равенства 8 + 2 = 10 . Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8 . Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2 есть разность числа 10 и числа 8
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство 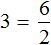
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
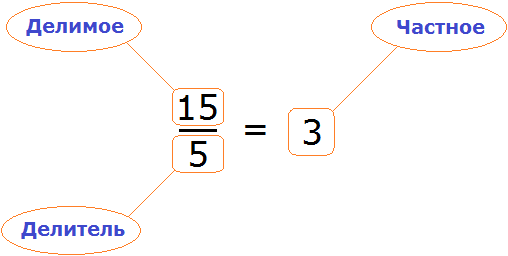
Пример 4. Рассмотрим равенство
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Видео:Уравнения. Основные понятия.Скачать

Правила нахождения неизвестных
Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.
В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.
Чтобы выразить число 2, мы поступили следующим образом:
То есть из суммы 10 вычли слагаемое 8.
Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x
В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10 , а переменная x берет на себя роль так называемого неизвестного слагаемого
Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10 . Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10 . Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8
А сейчас, чтобы найти неизвестное слагаемое x , мы должны из суммы 10 вычесть известное слагаемое 8:
Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x
Мы решили уравнение. Значение переменной x равно 2 . Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:
В результате получается верное числовое равенство. Значит уравнение решено правильно.
Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.
В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x , нужно из суммы 10 вычесть известное слагаемое 2
Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.
В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность
Чтобы выразить число 8, мы поступили следующим образом:
То есть сложили разность 6 и вычитаемое 2.
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x
В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого
Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6 . Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
А сейчас, чтобы найти неизвестное уменьшаемое x , мы должны к разности 6 прибавить вычитаемое 2
Если вычислить правую часть, то можно узнать чему равна переменная x
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного вычитаемого
Для нахождения неизвестного вычитаемого предусмотрено следующее правило:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.
А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6
Вычисляем правую часть и находим значение x
Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.
В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение
Чтобы выразить число 3 мы поступили следующим образом:
То есть разделили произведение 6 на множитель 2.
Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного множимого.
Для нахождения неизвестного множимого предусмотрено следующее правило:
Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.
Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6 . Произведение 6 мы разделили на множитель 2.
А сейчас для нахождения неизвестного множимого x , нужно произведение 6 разделить на множитель 2.
Вычисление правой части позволяет нам найти значение переменной x
Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:
Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.
Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6 . Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.
А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.
Вычисление правой части равенства 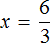
Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:
Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.
Например, решим уравнение 9 × x = 18 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9
Отсюда 
Решим уравнение x × 3 = 27 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3
Отсюда 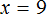
Вернемся к четвертому примеру из предыдущей темы, где в равенстве 
Чтобы выразить число 15 мы поступили следующим образом:
То есть умножили частное 3 на делитель 5.
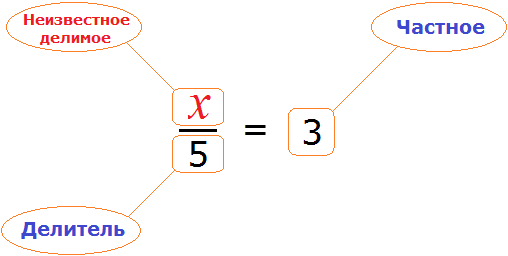
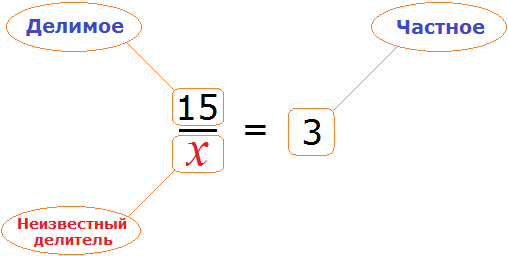
Теперь представим, что в равенстве 
В этом случае переменная x берет на себя роль неизвестного делимого.
Для нахождения неизвестного делимого предусмотрено следующее правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Что мы и сделали, когда выражали число 15 из равенства 
А сейчас, чтобы найти неизвестное делимое x , нужно частное 3 умножить на делитель 5
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Теперь представим, что в равенстве 
В этом случае переменная x берет на себя роль неизвестного делителя.
Для нахождения неизвестного делителя предусмотрено следующее правило:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Что мы и сделали, когда выражали число 5 из равенства 
А сейчас, чтобы найти неизвестный делитель x , нужно делимое 15 разделить на частное 3
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Итак, для нахождения неизвестных мы изучили следующие правила:
- Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
- Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
- Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
- Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
- Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
- Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
- Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Компоненты
Компонентами мы будем называть числа и переменные, входящие в равенство
Так, компонентами сложения являются слагаемые и сумма
Компонентами вычитания являются уменьшаемое, вычитаемое и разность
Компонентами умножения являются множимое, множитель и произведение
Компонентами деления являются делимое, делитель и частное
В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.
Пример 1. Найти корень уравнения 45 + x = 60
45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вычислим правую часть, получим значение x равное 15
Значит корень уравнения 45 + x = 60 равен 15.
Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.
Пример 2. Решить уравнение
Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x
В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.
При этом слагаемое 2x содержит переменную x . После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:
Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:
Вычислим правую часть получившегося уравнения:
Мы получили новое уравнение 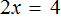
При этом переменная x является не просто множителем, а неизвестным множителем
Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:
Вычислим правую часть, получим значение переменной x
Для проверки найденный корень отправим в исходное уравнение 
Получили верное числовое равенство. Значит уравнение решено правильно.
Пример 3. Решить уравнение 3x + 9x + 16x = 56
Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.
Приведем подобные слагаемые в левой части данного уравнения:
Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
Отсюда x равен 2
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56 , мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56 . Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2 . Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56 , а затем в уравнение 28x = 56 , которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56 , которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 10 разделить на известный сомножитель 5.
Отсюда 
Вернемся к исходному уравнению 
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
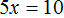

Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
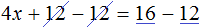
Получили уравнение 4x = 4 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 4 разделить на известный сомножитель 4
Отсюда
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12 . В результате получили равносильное уравнение 4x = 4 . Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x , а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда
Вернемся к исходному уравнению 
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
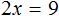

Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения 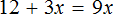
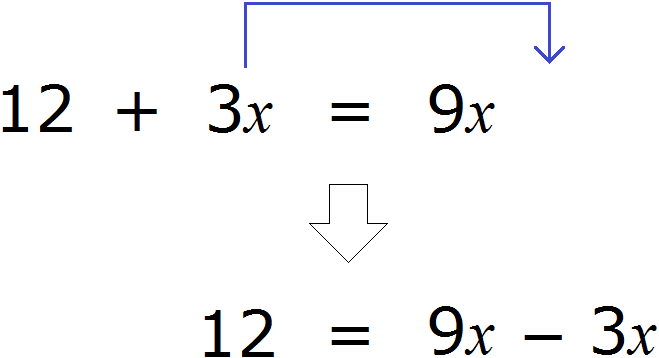
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x . Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда x = 2 . Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12 . В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению 
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение 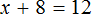

Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение 
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения 
Пример 2. Решить уравнение
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению 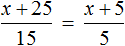
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15 . Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x . Корень этого уравнения, как и уравнения 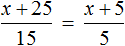
Пример 3. Решить уравнение
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение 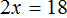
Отсюда
Вернемся к исходному уравнению 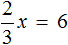
Получается верное числовое равенство. Значит уравнение решено правильно.
Пример 4. Решить уравнение
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x , сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x . Для этого разделим произведение 28 на известный сомножитель 7
Вернемся к исходному уравнению 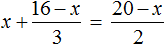
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A , а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно 

Видим, что значение переменной B , как и значение переменной A равно 
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42 . Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2 . Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14 , нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Умножение на минус единицу
Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.
Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1 .
Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.
Рассмотрим уравнение 
Прибавим к обеим частям уравнения число 5
Приведем подобные слагаемые:
А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения 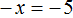
То есть минус, стоящий перед переменной x, относится не к самой переменной x , а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение 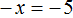
Имеем дело с компонентами умножения. Чтобы найти х , нужно произведение −5 разделить на известный сомножитель −1 .
или разделить обе части уравнения на −1 , что еще проще
Итак, корень уравнения 
Получилось верное числовое равенство. Значит уравнение решено верно.
Теперь попробуем умножить обе части уравнения 
После раскрытия скобок в левой части образуется выражение 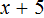
Корень этого уравнения, как и уравнения 
Значит уравнения 
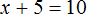
Пример 2. Решить уравнение
В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение 
Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.
Так, умножение уравнения 
либо можно просто поменять знаки всех компонентов:
Получится то же самое, но разница будет в том, что мы сэкономим себе время.
Итак, умножив обе части уравнения 
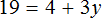
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на −1 . Тогда все компоненты поменяют свои знаки на противоположные:
Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:
Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:
Видео:Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать

Приравнивание к нулю
Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.
В качестве примера рассмотрим уравнение 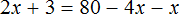
Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Приведем подобные слагаемые в левой части:
Прибавим к обеим частям 77 , и разделим обе части на 7
Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Альтернатива правилам нахождения неизвестных
Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.
К примеру, для нахождения неизвестного в уравнении 
Но если в уравнении 
Уравнения вида 
Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении 
Далее разделить обе части на 2
В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда 
Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:
В случае с уравнениями вида 
Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.
Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.
Видео:7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать

Когда корней несколько
Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9 .
В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9) , которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.
Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0 . Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0 . Несложно догадаться, что корень этого уравнения равен −9 . Проверка показывает, что корень верный:
Пример 2. Решить уравнение
Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2) . А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2) ).
Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:
Подставляем по-очереди найденные значения в исходное уравнение 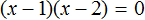
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Когда корней бесконечно много
Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
Пример 1. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14 . Это равенство будет получаться при любом x
Пример 2. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Когда корней нет
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение 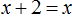
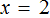
Пусть
Пример 2. Решить уравнение
Раскроем скобки в левой части равенства:
Приведем подобные слагаемые:
Видим, что левая часть не равна правой части. И так будет при любом значении y . Например, пусть y = 3 .
Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Буквенные уравнения
Уравнение может содержать не только числа с переменными, но и буквы.
Например, формула нахождения скорости является буквенным уравнением:
Данное уравнение описывает скорость движения тела при равноускоренном движении.
Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения 
Умнóжим обе части уравнения 
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении левую и правую часть поменяем местами:
У нас получилась формула нахождения расстояния, которую мы изучали ранее.
Попробуем из уравнения 
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении v × t = s обе части разделим на v
В левой части переменные v сократим на v и перепишем то, что у нас осталось:
У нас получилась формула определения времени, которую мы изучали ранее.
Предположим, что скорость поезда равна 50 км/ч
А расстояние равно 100 км
Тогда буквенное уравнение 
Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t . Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t
либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t
Затем разделить обе части на 50
Пример 2. Дано буквенное уравнение 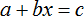
Вычтем из обеих частей уравнения a
Разделим обе части уравнения на b
Теперь, если нам попадется уравнение вида a + bx = c , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.
Решим уравнение 2 + 4x = 10 . Оно похоже на буквенное уравнение a + bx = c . Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:
Видим, что второе решение намного проще и короче.
Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0) , поскольку деление на ноль на допускается.
Пример 3. Дано буквенное уравнение 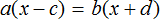
Раскроем скобки в обеих частях уравнения
Воспользуемся переносом слагаемых. Параметры, содержащие переменную x , сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.
В левой части вынесем за скобки множитель x
Разделим обе части на выражение a − b
В левой части числитель и знаменатель можно сократить на a − b . Так окончательно выразится переменная x
Теперь, если нам попадется уравнение вида a(x − c) = b(x + d) , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.
Допустим нам дано уравнение 4(x − 3) = 2(x + 4) . Оно похоже на уравнение a(x − c) = b(x + d) . Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d . Это позволит нам не ошибиться при подстановке:
Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0) . Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.
Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d) . В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:
Пример 4. Дано буквенное уравнение 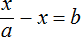
Приведем левую часть уравнения к общему знаменателю:
Умнóжим обе части на a
В левой части x вынесем за скобки
Разделим обе части на выражение (1 − a)
Видео:Алгебра 9 класс. Системы уравнений, основные понятия, расстояние между точкамиСкачать

Линейные уравнения с одним неизвестным
Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.
Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».
Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2 (x + 3) = 16 . Давайте решим его.
Раскроем скобки в левой части уравнения, получим 2 x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2 x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x , разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.
Уравнение 2 (x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10 , для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».
Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.
Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x . Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Если в линейном уравнении a = 0 и b = 0 , то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0 . При любом значении x левая часть будет равна правой части.
Если в линейном уравнении a = 0 и b ≠ 0 , то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5 . Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.
Если в линейном уравнении a ≠ 0 , и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3 , и b равно какому-нибудь числу, скажем числу 6 , то уравнение 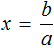
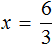
Отсюда 
Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0 . Это то же самое уравнение, что и ax = b , но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0 . Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.
В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.