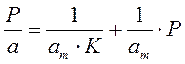Небольшая предыстория . В ходе изучения ПАВ американский химик и физик Ирвинг Ленгмюр выдвинул и математически обосновал идею об особом строении адсорбционных слоев. Он рассматривал ненасыщенный слой как двухмерный газ. По мере того как концентрация ПАВ увеличивается, происходит процесс, аналогичный конденсации двухмерного газа – молекулы образуют двухмерную пленку, которую Ленгмюр рассматривал как двухмерную жидкость. Если концентрация ПАВ в растворе неограниченно возрастает, то наступает момент предельного насыщения адсорбционного слоя, который приобретает вид частокола, так как предполагается, что слой имеет толщину, соответствующую длине адсорбированной молекулы. При этом адсорбция достигает предела. Эта теория была названа теорией мономолекулярного слоя, или монослоя.
Теория Ирвинга Ленгмюра(1914-1918) явилась фундаментальным вкладом в учение об адсорбции. Она позволяет учесть наиболее сильные отклонения от закона Генри, связанные с ограниченностью поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества.
Теория мономолекулярной адсорбции основывается на следующих положениях:
1) Адсорбция является локализованной (происходит на адсорбционных центрах).
2) Адсорбция происходит не на всей поверхности адсорбента, а на активных центрах, которыми являются выступы либо впадины на поверхности адсорбента. Активные центры считаются независимыми (т.е. один активный центр не влияет на адсорбционную способность других), и тождественными.
3) Каждый активный центр способен взаимодействовать только с одной молекулой адсорбата; в результате на поверхности может образоваться только один слой адсорбированных молекул.
4) Процесс адсорбции находится в динамическом равновесии с процессом десорбции.
На основании этих положений можно получить уравнение изотермы адсорбции. Скорость адсорбции из газовой фазы V ад (т.е число молекул, адсорбированных за единицу времени) пропорциональна давлению газа и числу свободных центров на поверхности твердого тела. Если общее число центров a ∞ ,а при адсорбции оказывается занятыми a центров, то число центров, остающийся свободными равно ( a ∞ — a ). Поэтому:
Адсорбция динамически уравновешена процессом десорбции. Скорость десорбции пропорциональна числу адсорбированных молекул:
Переобозначаем k ад / k дес = b (где b –это константа адсорбированного равновесия),получаем
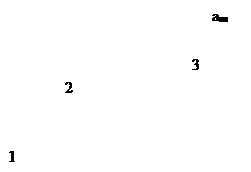
I — почти горизонтальный участок, который соответствует большим концентрациям, отвечает поверхности адсорбента, полностью насыщенным адсорбтивом. Величина удельной адсорбционной способности в этом случае не зависит от равновесной концентрации адсорбтива в растворе, что свидетельствует об образовании на поверхности мономолекулярного слоя.Описывается уравнением Генри:
II — соответствует промежуточным степеням заполнения поверхности.Описывается уравнением Фрейндлиха
III -почти все адсорбционные центры уже заняты и свободных центров на поверхности почти нет.
Уравнение Ленгмюра содержит два параметра, характеризующих адсорбцию. Это константа адсорбционного равновесия b и величина предельной адсорбции a ∞ , соответствующая полной полному заполнению поверхности мономолекулярным слоем адсорбата .
Для определения численных значений a ∞ и b уравнение Ленгмюра можно представить в виде:
С помощью линеаризации уравнения Ленгмюра можно определить предельную величину адсорбции a ∞ , соответствующую полному мономолекулярному покрытию адсорбента молекулами адсорбата.
Экспериментальное определение a ∞ позволяет рассчитать удельную поверхность адсорбента S уд:
где NA — постоянная Авагадро, W — площадь, приходящаяся на единичную молекулу адсорбата в мономолекулярном слое.
Однако,следует отметить некоторое развитие в положениях теории:
Во-первых,адсорбционные центры таки могут иметь разную энергию.
И в этом случае a ∞ будет рассчитываться как сумма всех различных центров:
Во-вторых,молекулы могут взаимодействовать между собой.
И наконец,на один адсорбционный центр может приходиться несколько молекул.
Т.е молекула первого слоя может являться вторичным центром.Это положение описывает теория о полимолекулярной адсорбции(теория БЭТ),но это уже совсем другая история 🙂
1.Левченко С.И. [Электронный ресурс] // Физическая и коллоидная химия.4.1.4Поверхностные явления и адсорбция.
2.Пальтиель Л.Р. [Электронный ресурс] // Коллоидная химия.8.Теория мономолекулярной адсорбции Ленгмюра
3. Журнал «Горизонт чистоты»[Электронный ресурс] //Теоретические основы клининга.2.5. Адсорбция ПАВ на границе раздела «жидкость-газ»
Видео:Уравнение ЛенгмюраСкачать
Теория мономолекулярной адсорбции Ленгмюра
Адсорбция на твердой поверхности была известна уже в конце ХVIII века. Наиболее ранние работы по применению углей для очистки веществ методом адсорбции и разработке теории открытого им явления выполнены петербургским академиком Т.Е. Ловицем (1789). Для объяснения адсорбции Ловиц использовал существовавшую тогда теорию флогистона.
Первое уравнение, использующее молекулярно-кинетическую теорию и связывающее количество адсорбированного вещества с равновесным давлением его в газовой фазе, дал американский ученый И. Ленгмюр (1919).
и. Ленгмюр (1881-1957) разработал теорию адсорбции на твердом теле и вывел уравнение изотермы адсорбции. Достоинство уравнения Ленгмюра заключается в том, что оно имеет теоретическое обоснование и не содержит поверхностного натяжения, не поддающегося измерению для твердых поверхностей.
Выводя уравнение, Ленгмюр исходил из определенных представлений, сущность которых сформулирована в его теории.
Основные положения теории Ленгмюра:
– поверхность твердого тела в отличие от поверхности жидкости неоднородна вследствие того, что положение атомов (молекул, ионов) здесь фиксировано, поверхность имеет выступы, изломы, трещины (рис.9.22);
 |
Рис. 9.22. Поверхность твердого тела при большом увеличении
– адсорбция происходит не на всей поверхности, а только на активных центрах. Такими центрами служат узлы кристаллической решетки, выступы, возвышения на гладкой поверхности, размеры которых сами по себе очень невелики, но весьма значительны по сравнению с размерами атомов и молекул;
– каждый активный центр удерживает только одну молекулу силами остаточной валентности, действующими на расстоянии молекулярной сферы. Это значит, что адсорбционные силы отождествляются с химическими валентными силами;
– когда все активные центры заняты, наступает адсорбционное насыщение, и дальнейшая адсорбция невозможа. Отсюда следует, что адсорбтив располагается на поверхности адсорбента мономолекулярным слоем;
– адсорбированные молекулы остаются некоторое время связанными с активными центрами, а затем покидают поверхность (десорбируются);
– для упрощения силы межмолекулярного взаимодействия между адсорбированными молекулами не учитываются.
Свою теорию Ленгмюр вывел для случая адсорбции газообразных веществ на твердых поверхностях.
Состояние равновесия определяется равенством скоростей адсорбции и десорбции. Каждая молекула задерживается некоторое время на поверхности, поэтому поверхность всегда частично покрыта адсорбционным слоем. Величина покрытия растет с ростом продолжительности пребывания молекул на поверхности, что, в свою очередь, зависит от силы взаимодействия между адсорбированными молекулами и адсорбционными центрами.
Если число активных мест поверхности принять равным единице, а долю активных мест, занятых адсорбированными молекулами, обозначить через, Q то свободная часть поверхности равна 1- Q. Величина Q равна отношению количества адсорбированного вещества А к максимальной адсорбции А¥ при полном заполнении поверхности:
1 – число активных мест поверхности,
Q – доля активных мест, занятых адсорбированными молекулами,
(1 – Q) – свободная часть поверхности, тогда
При постоянной температуре в момент равновесия скорость адсорбции Va равна скорости десорбции Vд. Скорость адсорбции пропорциональна давлению газа Р и свободной поверхности (1 – Q), т.е.
где К а — коэффициент пропорциональности, или константа скорости адсорбции.
Десорбция происходит только с занятой поверхности, поэтому
где Кд — константа скорости десорбции.
Решая это выражение в отношении Q, получим:
Q =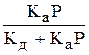 
(9.49)
Разделив числитель и знаменатель на Кд, обозначив Ка/ Кд через К и заменив Q = A/A¥ , окончательно получим:
А = А¥ 
, (9.50)
где К – константа адсорбционного равновесия.
В случае адсорбции из раствора уравнение Ленгмюра выводится аналогично и имеет вид:
А = А¥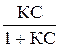 
, (9.51)
где С — равновесная концентрация адсорбируемого вещества в растворе.
Уравнения (9.50) и (9.51) носят название уравненияизотермы мономолекулярной адсорбции Ленгмюр. Они хорошо описывают адсорбцию как при малом, так и при большом давлении газа (или концентрации растворенного вещества).
Необходимо отметить, что константа адсорбционного равновесия в уравнении Ленгмюра (К) характеризует энергию взаимодействия адсорбата с адсорбентом. Чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия.
Проанализируем уравнение, проэкстраполируем его на малые и большие значения давления адсорбируемого газа (Р).
Рассмотрим знаменатель дроби. При малом давлении газа 1 >> КР и величиной КР можно пренебречь, знаменатель прев-ращается в 1; тогда
т.е. уравнение приобретает вид, тождественный с уравнением Генри. При малом давлении адсорбция пропорциональна давлению (концентрации).
При большом давлении (концентрации) можно, наоборот, пренебречь единицей (по сравнению с КР), тогда
т.е. адсорбция количественно достигает такого предела, когда все активные центры заняты и адсорбция перестает зависеть от давления (концентрации). Соотношение (9.53) отвечает насыщению, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата.
Экспериментальное определение А¥ позволяет рассчитать удельную поверхность адсорбента:
где А¥ – предельная адсорбция, выраженная числом молей адсорбата на единицу массы адсорбента;
NA – число Авогадро;
w – площадь, занимаемая одной молекулой адсорбата.
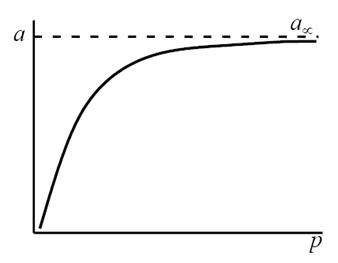
Уравнению Ленгмюра соответствует простейшая форма изотермы адсорбции — кривая насыщения, отвечающая образованию мономолекулярного адсорбционного слоя (рис. 9.23).
Рассмотрим определение констант уравнения Ленгмюра (константы адсорбционного равновесия и величины предельной адсорбции).
Константы А¥ и К удобно определять графически. Для этого преобразуем уравнение изотермы адсорбции Ленгмюра: возведем обе части этого уравнения в степень « -1».
(9.55)
Рис. 9.23. Изотерма адсорбции по Ленгмюру
 |
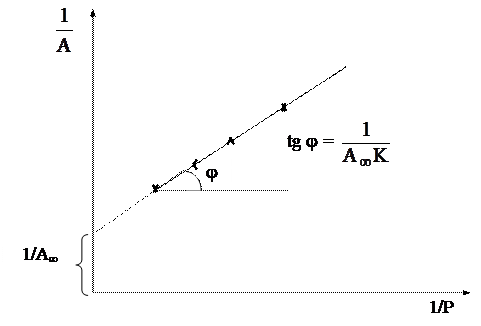Рис.9.24. Графический способ определения констант А¥ и К
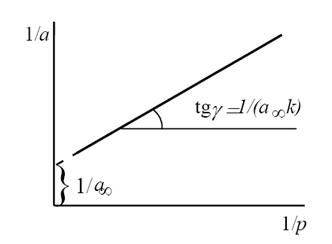
Полученное выражение представляет собой линейную зависимость : 1/А = f (1/Р) (рис.9.24), в которой 1/(К А¥) — тангенс угла наклона прямой, а 1/ А¥ — длина отрезка на оси ординат, отсекаемого продолжением графика функции 1/А = f (1/Р).
Для построения графика, приведенного на рис. 9.24, необходимо экспериментально определить величину адсорбции для нескольких значений давления газа (или для нескольких концентраций растворенного вещества).
Уравнение Ленгмюра описывает процесс адсорбции с молекулярно – кинетических позиций, в то время как уравнение Гиббса с термодинамических позиций. В уравнение Гиббса входит поверхностное натяжение, которое является практически не определяемой величиной для твердых поверхностей. Из уравнения Гиббса следует, что при адсорбции происходит уменьшение поверхностного натяжения, то есть уменьшение свободной поверхностной энергии (что и является причиной адсорбции).
Рассмотрим взаимосвязь уравнений Гиббса и Ленгмюра, с разных позиций описывающих процесс адсорбции.
Снижение поверхностного натяжения s с возрастанием концентра-ции Сописывается эмпирическим уравнением Б.А. Шишковского, предложенным им в 1908 году:
Ds = s0 — s = В ln (КС + 1) (9.56)
где Ds — разность поверхностного натяжения чистого растворителя (s0) и раствора (s) с концентрацией С;
А и В — постоянные, значения которых находят из опыта.
Пользуясь уравнением Шишковского в дифференциированном виде, можно перейти от уравнения Гиббса к уравнению Ленгмюра.
Продифференцируем уравнение Шишковского, учитывая, что дифференциал от постоянной величины s0 равен 0, а дифференциал d(Bln(KC + 1)) = (ВК/(КС+1)) dС.
d(s – s0) = d(Bln(KC + 1)), отсюда
ds = 
С (9.57)
Разделим обе части на dС
(9.58)
Из уравнения Гиббса
Г = 
выразим 
и подставим в выражение (9.58)
(9.59)
Выразим из этого уравнения величину Г
(9.60)
Это уравнение аналогично уравнению Ленгмюра при условии, что Г = А (это практически одно и то же);
– величина предельной адсорбции;
К – константа адсорбционного равновесия.
Отсюда А = А¥ 
Таким образом, мы пришли к уравнению Ленгмюра. Следовательно, уравнение Шишковского является тем переходным мостом, который соединяет уравнение Гиббса, выведенное исходя из термодинамических представлений, и уравнение Ленгмюра, выведенное на основе молекуляр-но-кинетических положений.
Из выражения (9.60) становится ясным смысл эмпирических констант К и В из уравнения Шишковского:
К – константа адсорбционного равновесия, которая будет иметь разное значение для разных представителей одного гомологического ряда;
Так как величина А¥ одинакова для всех членов любого гомологического ряда (молекулы ПАВ занимают одинаковую площадь в мономолекулярном адсорбционном слое) и мало различается для обычных ПАВ (жирные кислоты, спирты и т.д.), становится понятным, почему В является постоянной величиной для всего гомологического ряда при постоянной температуре.
Таким образом, уравнение Гиббса, характеризующее изменение поверхностного натяжения растворов при адсорбции, может быть приведено к уравнению Ленгмюра, выведенному для адсорбции газов на твердых адсорбентах.
Отсюда следует, что адсорбция различных веществ на различных поверхностях раздела фаз подчиняется одним и тем же закономерностям.
Очевидно, что адсорбция молекул на твердых поверхностях приво-дит к уменьшению поверхностного натяжения на границе твердое тело – газ, хотя в отличие от жидких поверхностей опытным путем это установить невозможно.
Отсюда становится очевидной и причина адсорбции – это стремление к уменьшению свободной поверхностной энергии (т.е. поверхностного натяжения).
Видео:Практическое занятие 5. Уравнение БЭТ. Удельная поверхностьСкачать
Уравнение изотермы адсорбции Ленгмюра
Конечно, предположение, что молекулы адсорбируются с одинаковой вероятностью на любых участках поверхности, в том числе и уже занятых ранее — слишком грубое допущение, пригодное лишь для очень малых степеней покрытия.
Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.
1) Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.
2) Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.
3) Адсорбированные молекулы не взаимодействуют друг с другом.
Простейший вывод уравнения Ленгмюра, данный Кисилевым, основан на рассмотрении химического (в случае хемосорбции) или квазихимического (в случае физической адсорбиии) равновесия молекула газа + свободное место↔адсорбированная молекула.
Для обычного выражения константы равновесия через концентрации участников рассматриваемого процесса необходимо условиться о способах их выражения. Концентрация адсорбированных молекул может быть выражена не только числом адсорбированных молекул на 1 м 2 поверхности, но и в относительных единицах через долю занятой поверхности (степень заполнения поверхности) θ. Тогда, в тех же единицах, концентрация свободных мест 1-θ. Концентрация молекул газа (а молях на миллилитр) может быть заменена пропорциональной ей величиной давления Р (равновесное давление адсорбата в объеме фазы, граничащей с адсорбентом). Такая свобода в выборе единиц рассматриваемых концентраций обусловлена тем, что соответствующие константы пропорциональности могут быть объединены с константой равновесия. Итак, константа равновесия
. (2.6)
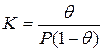
Решение этого уравнения относительно θ приводит к выражению
. (2.7)
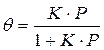
Если а, как и раньше, есть величина адсорбции (моль/см 2 или см 3 /г), а am — величина адсорбции, соответствующая полному заполнению поверхности (емкость монослоя, моль/см 2 ), то степень заполнения θ=a/am, (2.8)
т.е.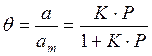 
, (2.9)
отсюда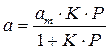 
(2.10)
В такой форме уравнение Ленгмюра широко известно. Оно содержит две константы: am, кратко называемая емкостью монослоя, и K — константа, зависящая от энергии адсорбции и температуры.
Итак, уравнение Ленгмюра – это уравнение монослойной адсорбции на однородной поверхности в отсутствие сил притяжения между молекулами адсорбата.
Посмотрим, какую форму примет уравнение при крайних значениях поверхностной концентрации адсорбированного вещества.
В области малых концентраций, т.е. при малых давлениях, КР >1, и единицей в знаменателе можно пренебречь:
т.е. величина адсорбции стремится к пределу, при котором она уже практически не зависит от давления (участок 3 изотермы адсорбции). В промежуточной области (участок 2) зависимость адсорбции от давления описывается самим уравнением (2.10).
Рис. 2.5. Три участка изотермы адсорбции Ленгмюра
Таким образом, по модели Ленгмюра, вначале адсорбция растет пропорционально давлению газа, затем, по мере заполнения мест на поверхности, этот рост замедляется и, наконец, при достаточно высоких давлениях рост адсорбции практически прекращается, так как покрытие поверхности становится весьма близким к монослойному. Необходимо подчеркнуть, однако, что по этой модели завершение образования монослоя происходит лишь при бесконечно высоком давлении. Форма изотермы адсорбции, предсказываемая уравнением Ленгмюра, экспериментально наблюдается в случае химической адсорбции на однородных поверхностях. Для физической адсорбции такое соответствие наблюдается только в начальной области изотермы. При больших заполнениях не получается предсказываемого теорией приближения к насыщению и изотерма продолжает подъем с ростом давления, причем она становится даже более крутой.
Для удобной проверки приложимости уравнения Ленгмюра к экспериментальным данным преобразуем его в линейную форму. Разделим обе части уравнения (2.10) на Р:
. (2.13)
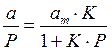
Перевернем дроби по обе части равенства:
. (2.14)
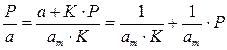
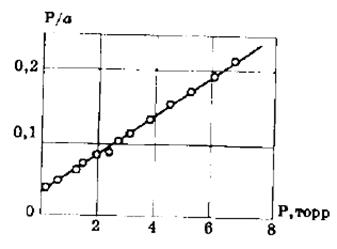
Если по оси абсцисс откладывать Р, а на оси ординат Р/а, то в случае выполнимости уравнения Ленгмюра экспериментальные точки должны укладываться на прямую. Начальной ординатой будет 1/(аm∙К), тангенсом угла наклона прямой 1/аm. Из того и другого выражения легко вычислить обе константы am и К. Пример такого построения показан на рис. 2.6, где экспериментальные точки для адсорбции бензола на графитированной саже, в соответствии с указанными ранее, легли па прямую только в области малых давлений (до Р/Р0 =0.1).
Рис. 2.6. Изотерма адсорбции бензола при 20 о С на графитированной саже в координатах линейной формы уравнения Ленгмюра
Имеется немало примеров, когда уравнение Ленгмюра не выполняется. Объясняется это тем, что не оправдываются оба допущения теории об однородности поверхности и отсутствии взаимодействия молекул, особенно первое из них. Тот факт, что имеются случаи адсорбции на реальных неоднородных поверхностях, когда уравнение Ленгмюра все же удовлетворительно описывает экспериментальные данные, Брунауер объясняет тем, что в некотором интервале адсорбция происходит не на всей поверхности адсорбента, а только на части ее, именно на местах с примерно одинаковой теплотой адсорбции. Тогда в этом интервале уравнение Ленгмюра будет справедливо. После того, как эти места заполнены, начинает заполняться следующая серия мест с меньшей теплотой адсорбции. Поэтому для совокупности всех мест поверхности уравнение Ленгмюра может быть непригодно, а для части этих мест — справедливо. Отсюда, выполнимость его для разных адсорбентов зависит от соотношения участков с разной теплотой адсорбции.
Константы уравнения (2.10) K и am могут быть определены графическим способом (рис. 2.7). Для этого уравнение Ленгмюра приводят к следующему линейному виду, разделив единицу на уравнение (2.10):
(2.15)
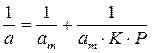
Рис. 2.7. Линейная форма уравнения изотермы Ленгмюра (a∞=am)
Зная емкость монослоя, можно определить удельную поверхность адсорбента Sуд (м 2 /г или см 2 /г) если известна площадь ω, занимаемая частицей в плотном адсорбционном слое (площадь, занимаемая одной молекулой азота в адсорбционном слое ω = 0.162 нм 2 ):
, (16)
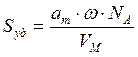
где аm — емкость монослоя — это количество адсорбата, которое может разместиться в полностью заполненном адсорбционном слое толщиной в 1 молекулу — монослое – на поверхности единицы массы (1г) твердого тела; ω — средняя площадь, занимаемая молекулой адсорбата в заполненном монослое, NA — число Авогадро (6,022·10 23 молекул/моль); VM — молярный объем адсорбата (газа) (VM = 22,41 л/моль=22,41∙10 -3 м 3 /моль).
Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.
Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию В этом случае используют уравнение БЭТ (Брунауер –Эммет — Теллер).
Пример 2.1. При адсорбции азота на активированном угле при 220К получены следующие данные:
Р, Па 5310 9800 18000 33000 70000
a, cм 3 /г 7 14 23 32 51
Плотность газообразного азота ρ=1,2506 кг/м 3 . Площадь, занимаемая одной молекулой азота в насыщенном монослое, составляет ω = 0.162 нм 2 . VM — молярный объем адсорбата (газа) (VM = 22,41 л/моль=22,41∙10 -3 м 3 /моль).
Постройте изотерму адсорбции в линейных координатах. Графически определите константы аm и К уравнения Ленгмюра, пользуясь которыми, постройте изотерму Ленгмюра. Определите удельную поверхность активированного угля Sуд.
Решение. Линейная форма уравнения Ленгмюра выражается (2.15):
.
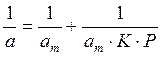
Определим 1/аm и 1/ р:
(1/р)·10 -3 , Па 0,1883 0,1020 0,0556 0,0303 0,0143
1/а·, см 3 /г 0,143 0,071 0,043 0,031 0,020
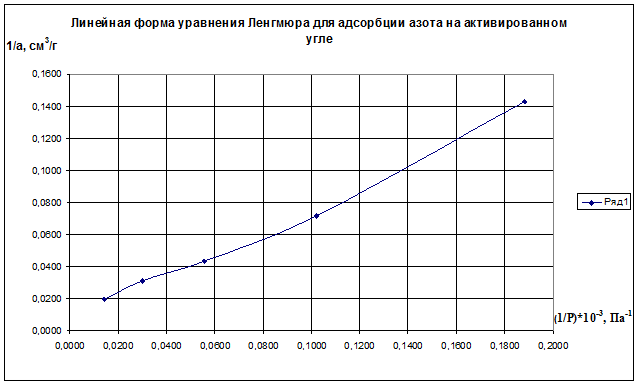
Строим график зависимости 1/а=f(1/р)∙10 -3 (рис.2.8). По графику находим 1/аm как отрезок, отсекаемый прямой на оси ординат, для чего необходимо продлить полученную прямую до пересечения с осью ординат.
Рис.2.8. Линейная форма уравнения Ленгмюра для адсорбции азота на активированном угле
Уравнение прямой y=a+bx, имеет следующее формульное выражение:
Это выражение может быть определено с помощью регрессионного анализа в Microsoft Excel (встроенного пакета Анализ данных — Регрессия по значениям 1/аm и 1/ р).
Из уравнения получим 1/am=0,00698 г/см 3 .
Откуда получим: am=143,35 см 3 /г.
Далее находят тангенс угла наклона прямой к оси абсцисс tgα=1/(am∙K) по графику (или по уравнению регрессии). tgα=0,70099. Тогда, зная значения am и tgα, можно определить K=9,95 кг/м 3 .
Теперь, зная константы аm и К уравнения Ленгмюра, построим изотерму Ленгмюра, для чего рассчитаем по формуле (2.10) значения а для различных значений Р и получим:
Р, Па 5310 9800 18000 33000 70000
a, cм 3 /г 140,69 141,90 142,56 142,92 143,15
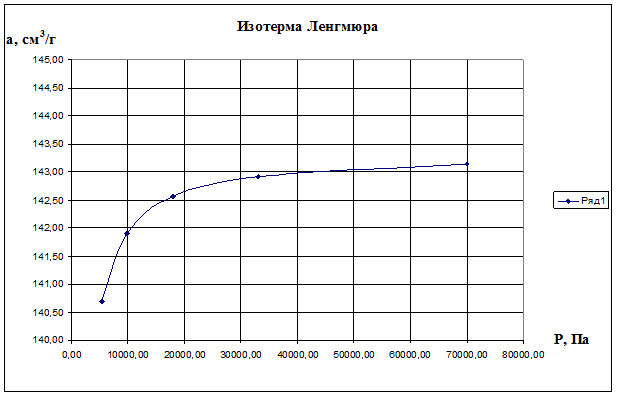
По данным значениям построим изотерму Ленгмюра а=f(P), представлена на рис.2.9.
Рис. 2.9. Изотерма Ленгмюра а=f(P)
По формуле (2.16) рассчитаем удельную поверхность активированного угля: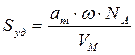 
и получим Sуд=624,05 м 2 /г.
В случае, когда известна плотность вещества (адсорбента) ρ и молярная масса M, а не известен VM — молярный объем адсорбата удельную поверхность вещества (активированного угля) находят по формуле:
где am выражают в моль/кг.
Для азота М= 0,0280 кг/моль, ρ=1,2506 кг/м 3 .
Из расчетов видно, что два способа расчета Sуд дают почти одинаковые результаты.
Пример 2.2. Удельная поверхность непористой сажи равна 73,7м 2 /кг. Рассчитайте площадь, занимаемую молекулой бензола в плотном монослое, исходя из данных об адсорбции бензола на этом адсорбенте при 293 К.
Р, Па 1,03 1,29 1,74 2,50 6,67
а∙10 2 , моль/кг 1,57 1,94 2,55 3,51 7,58
Предполагается, что изотерма адсорбции описывается уравнением Ленгмюра.
Решение. Используем линейную форму записи уравнения Ленгмюра, заданную формулой (2.14):
Рассчитываем значения Р/а:
(Р/а)∙10 -2 , Па∙кг/моль 0,656 0,668 0,68 0,712 0,879
Р, Па 1,03 1,29 1,74 2,50 6,67
По этим данным строим график в координатах уравнения Ленгмюра в линейной форме P/a=f(P).
Из графика находим аm= Р/(Р/а) = 25,2∙10 -2 моль/кг.
Удельная поверхность адсорбента связана с емкостью слоя аm, выраженного в моль/кг, соотношением: Sуд=am∙ω∙NA (2.18)
Площадь, занимаемая молекулой бензола в плотном монослое, равна
ω = Sуд/(am NA) ==73,7 10 3 /(6,02 10 23 ∙25,210 -2 )=0,49∙10 -18 м 2 =0,49 нм 2 .
📺 Видео
5.1. Адсорбция. Классификация адсорбцииСкачать
Адсорбция на поверхностях растворовСкачать
Поверхностные явленияСкачать
Коробов М. В. - Физическая химия II - Основные положения теории активированного комплексаСкачать
Коробов М. В. - Физическая химия. Часть 1 - Адсорбция на границе газ-твердое. Модель ЛенгмюраСкачать
5.3. Адсорбция на границе жидкость-газ. Поверхностно активные вещества ПАВСкачать
Принцип наименьшего действия #2 - Уравнение Эйлера-ЛагранжаСкачать
Поверхностно-активные веществаСкачать
Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать
Поверхностные явления. Адсорбция.Скачать
Калужских А.Г.Лекция №4 «Поверхностные системы»Скачать
Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать
Практическое занятие 6. Адсорбция на границе раствор – газСкачать
Закон БернуллиСкачать
Коробов М. В. - Физическая химия. Часть 1 - Основные понятия, свойства системыСкачать
Химическая кинетика. Скорость химической реакции | ХимияСкачать
ФИЗИЧЕСКАЯ ХИМИЯ (ТЕРМОДИНАМИКА). ОСНОВНЫЕ ПОНЯТИЯ: СИСТЕМЫ, ПАРАМЕТРЫ, ФУНКЦИИСкачать
