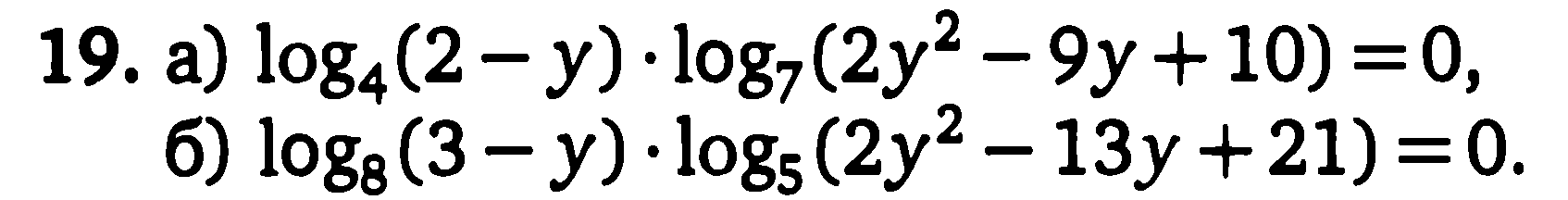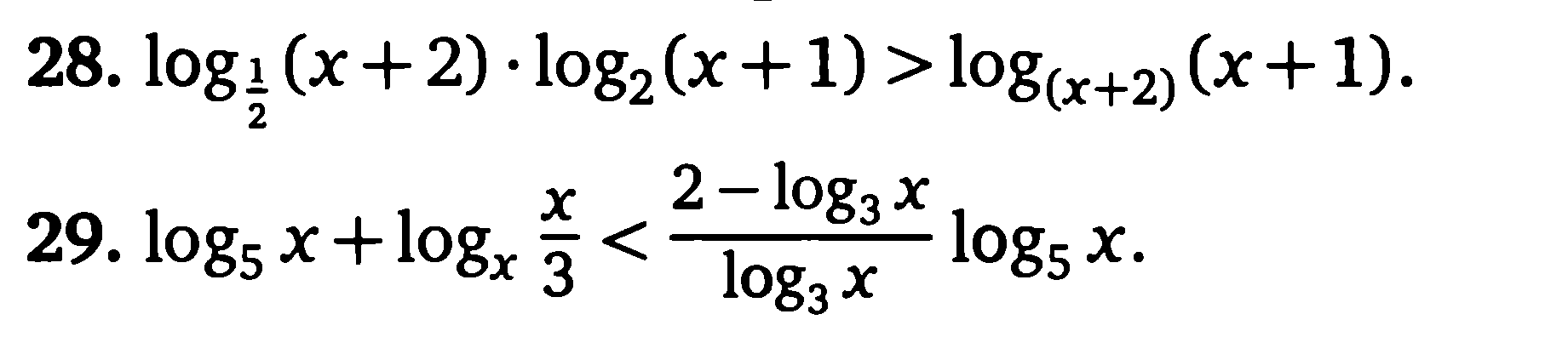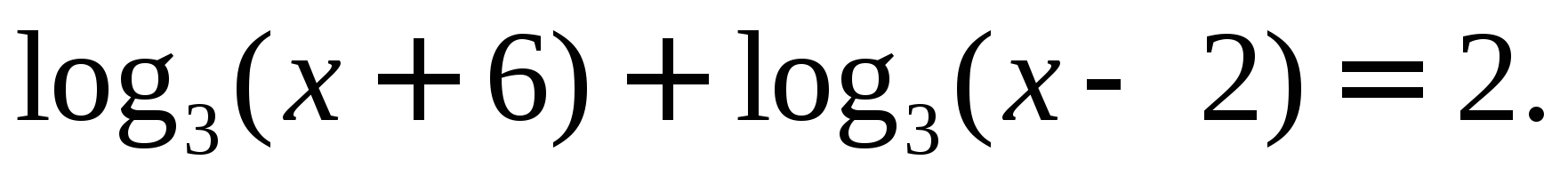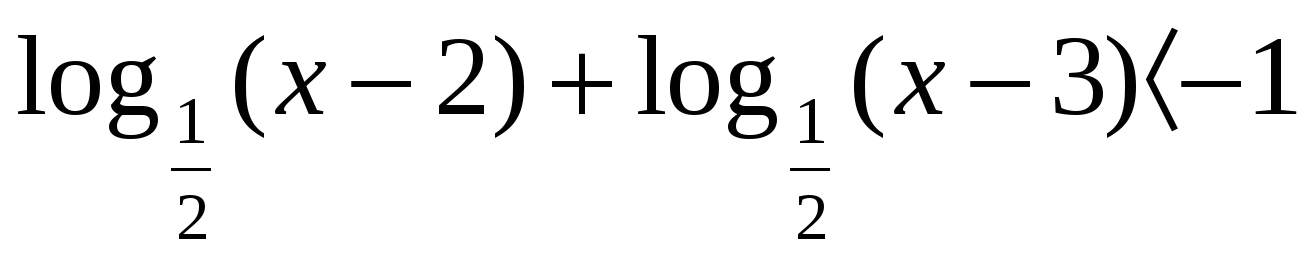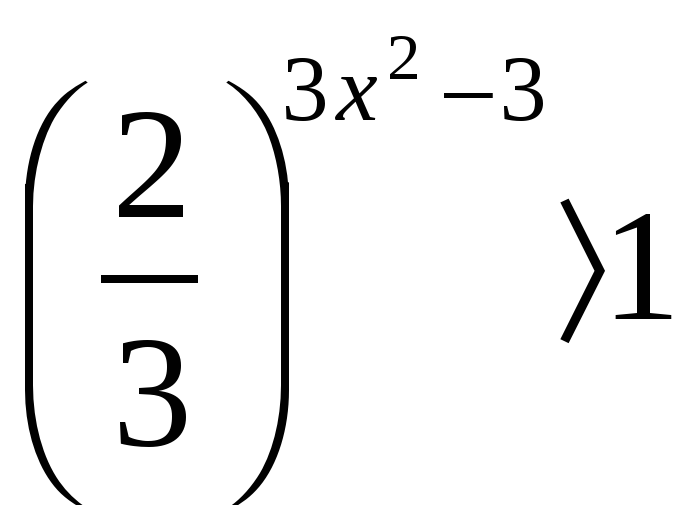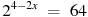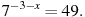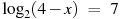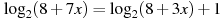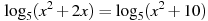Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
311 лекций для учителей,
воспитателей и психологов
Получите свидетельство
о просмотре прямо сейчас!
Методы решения показательных уравнений.
Показательным уравнением называется уравнение, содержащее переменную в показателе степени (к тому же, переменная может быть и в основании степени).
Для успешного решения показательных уравнений необходимо:
— безошибочно решать простейшие показательные уравнения.
— не только активно знать все показательные тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать «посторонних» корней, а тем более, — не терять решений уравнения.
— чётко, подробно и без ошибок проделывать математические преобразования
— знать методы решения задач. Для этого:
определить тип уравнения;
вспомнить соответствующий этому типу метод решения задачи.
Три разных основания степеней
Разложение оснований на множители и сведение к двум основаниям степени
Два разных основания степеней-
степени одного числа
Приведение к одинаковым показателям степеней
Приведение к одинаковым основаниям степеней
Два разных основания степеней-
Одинаковые основания степеней — разные показатели
Деление на меньшее основание в степени уравнения
Приведение к одинаковым показателям степеней
Одинаковые основания степеней — одинаковые показатели степеней
Приведение к одному основанию степени
Простейшие показательные уравнения
Методы решения показательных неравенств.
Показательным неравенством называется неравенство, содержащее переменную в показателе степени (к тому же, переменная может быть и в основании степени).
Для успешного решения показательных неравенств необходимо:
— безошибочно решать простейшие показательные неравенства.
— не только активно знать все показательные тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать «посторонних» решений, а тем более, — не терять решений неравенств.
— чётко, подробно и без ошибок проделывать математические преобразования
— знать методы решения задач. Для этого:
определить тип неравенств;
вспомнить соответствующий этому типу метод решения задачи.
Три разных основания степеней
Разложение оснований на множители и сведение к двум основаниям степени
Два разных основания степеней-
степени одного числа
Приведение к одинаковым показателям степеней
Приведение к одинаковым основаниям степеней
Два разных основания степеней-
Одинаковые основания степеней — разные показатели
Деление на меньшее основание в степени уравнения
Приведение к одинаковым показателям степеней
Одинаковые основания степеней — одинаковые показатели степеней
Приведение к одному основанию степени
Простейшие показательные неравенства
Логарифмирование и использование монотонности показательной функции
Методы решения логарифмических уравнений.
Логарифмическим уравнением называется уравнение, содержащее переменную под знаком логарифма и/или в основании логарифма.
, a>0, a
1 , x>0.
Для успешного решения логарифмических уравнений необходимо:
— безошибочно решать простейшие логарифмические уравнения.
— не только активно знать все логарифмические тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать «посторонних» корней, а тем более, — не терять решений уравнения.
— чётко, подробно и без ошибок проделывать математические преобразования
— знать методы решения задач. Для этого:
определить тип уравнения;
вспомнить соответствующий этому типу метод решения задачи.
Разные основания логарифмов
Приведение к одинаковым основаниям логарифмов
Одинаковые основания логарифмов — разные выражения под логарифмами
Приведение к одинаковым выражениям под логарифмами
Одинаковые основания логарифмов – одинаковые выражения под логарифмами
Сворачивание в один логарифм
Простейшие логарифмические уравнения
Необходимо всегда помнить, что логарифм определён при выполнении трёх условий:
— выражение под логарифмом больше нуля;
— основание логарифма больше нуля
— основание логарифма не равно единице.
Методы решения логарифмических неравенств.
Логарифмическим неравенством называется неравенство, содержащее переменную под знаком логарифма и/или в основании логарифма.
, a >0, a 1, x >0.
Для успешного решения логарифмических неравенств необходимо:
— безошибочно решать простейшие логарифмические неравенства.
— не только активно знать все логарифмические тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать «посторонних» корней, а тем более, — не терять решений уравнения.
— чётко, подробно и без ошибок проделывать математические преобразования
— знать методы решения задач. Для этого:
определить тип неравенства;
вспомнить соответствующий этому типу метод решения задачи.
Разные основания логарифмов
Приведение к одинаковым основаниям логарифмов
Одинаковые основания логарифмов — разные выражения под логарифмами
Приведение к одинаковым выражениям под логарифмами
Одинаковые основания логарифмов – одинаковые выражения под логарифмами
Сворачивание в один логарифм
Простейшие логарифмические уравнения
Потенцирование и использование монотонности логарифмической функции
Необходимо всегда помнить, что логарифм определён при выполнении трёх условий:
— выражение под логарифмом больше нуля;
— основание логарифма больше нуля
— основание логарифма не равно единице.
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Курс профессиональной переподготовки
- Математика: теория и методика преподавания в сфере начального общего образования
- Математика и информатика: теория и методика преподавания в образовательной организации
- Профилактика синдрома «профессионального выгорания» у педагогов
- «Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Методы решения показательных и логарифмических уравнений и неравенств
- Просмотр содержимого документа «Рефлексия»
- Просмотр содержимого документа «диагностическая карта»
- Просмотр содержимого документа «домашнее задание»
- Просмотр содержимого документа «конспект урока»
- Неравенства. Метод замены множителя (метод рационализации)
- Алгебра и начала математического анализа. 11 класс
- 🎬 Видео
Математика: теория и методика преподавания в сфере начального общего образования
- Сейчас обучается 75 человек из 31 региона
Курс профессиональной переподготовки
Математика и информатика: теория и методика преподавания в образовательной организации
- Сейчас обучается 575 человек из 71 региона
Курс повышения квалификации
Профилактика синдрома «профессионального выгорания» у педагогов
«Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 856 702 материала в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 17.12.2015
- 1499
- 1
- 17.12.2015
- 612
- 0
- 17.12.2015
- 368
- 0
- 17.12.2015
- 2942
- 36
- 17.12.2015
- 423
- 1
- 17.12.2015
- 875
- 0
- 17.12.2015
- 1890
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 17.12.2015 4277
- DOCX 75 кбайт
- 46 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Сатцаева Нонна Ефимовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 12470
- Всего материалов: 3
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:11 класс, 17 урок, Логарифмические уравненияСкачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
«Особенности общения с ребенком с УО»
«Коммуникативный педагогический тренинг: Способы взаимодействия с разными категориями учащихся»
«Как через игру развить сенсорные системы ребенка с особенностями»
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Тысячи учителей в Австралии вышли на забастовку
Время чтения: 2 минуты
ФИПИ опубликовал открытые варианты заданий ЕГЭ 2022 года
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать
Методы решения показательных и логарифмических уравнений и неравенств
Разработка обобщающего урока по теме «методы решения показательных и логарифмических уравнений и неравенств» , конспект + презентация.
Просмотр содержимого документа
«Рефлексия»
На уроке я работал
Своей работой на уроке я
доволен / не доволен
Урок для меня показался
не устал / устал
стало лучше / стало хуже
Материал урока мне был
понятен / не понятен
Домашнее задание мне кажется
интересно / не интересно
На уроке я работал
Своей работой на уроке я
доволен / не доволен
Урок для меня показался
не устал / устал
стало лучше / стало хуже
Материал урока мне был
понятен / не понятен
Домашнее задание мне кажется
интересно / не интересно
Просмотр содержимого документа
«диагностическая карта»
Этапы работы на уроке
1. Решение простейших логарифмических уравнений и неравенств
2. Теоретические сведения о решении логарифмических уравнений и неравенств
4. Работа в группах
Этапы работы на уроке
1. Решение простейших логарифмических уравнений и неравенств
2. Теоретические сведения о решении логарифмических уравнений и неравенств
4. Работа в группах
Этапы работы на уроке
1. Решение простейших логарифмических уравнений и неравенств
2. Теоретические сведения о решении логарифмических уравнений и неравенств
4. Работа в группах
Этапы работы на уроке
1. Решение простейших логарифмических уравнений и неравенств
2. Теоретические сведения о решении логарифмических уравнений и неравенств
4. Работа в группах
Этапы работы на уроке
1. Решение простейших логарифмических уравнений и неравенств
2. Теоретические сведения о решении логарифмических уравнений и неравенств
4. Работа в группах
Просмотр содержимого документа
«домашнее задание»
Просмотр содержимого документа
«конспект урока»
Тема урока: Методы решения показательных и логарифмических уравнений и неравенств.
Цели урока: урок обобщения и систематизации знаний и способов действий в сочетании с их комплексным применением.
создать условия для повторения и обобщения знаний учащихся по теме «Решение логарифмических уравнений и неравенств»;
активизировать деятельность учащихся по применению комплекса знаний и умений на практике;
подготовка к ЕГЭ.
развивать способности применять теоретические знания на практике;
развивать навыки работы с тестовыми заданиями;
развивать навыки самоконтроля , логическое мышление, память, внимание.
воспитывать ответственное отношение к изучению математики, трудолюбие, взаимопомощь, волю и настойчивость в достижении поставленной цели.
Оборудование урока: презентация, компьютер, проектор, интерактивная доска, карточки с тестовыми заданиями, диагностические карты.
Организация начала урока (Учащимся сообщается тема урока и цели, подчеркивается актуальность повторения данной темы для подготовки к ЕГЭ).
Девиз сегодняшнего урока: “Нельзя изучать математику глядя на то, как это делает сосед”.
Только свой труд в изучении математики может принести результаты. Перед нами стоит задача: повторить типы, методы и особенности решения показательных и логарифмических уравнений и неравенств и применить их на практике.
Наши знания должны работать и дать положительный результат на экзамене. Сегодня каждый из вас проведет диагностику своих знаний по данной теме, для этого у каждого диагностические карты, в которых вы оцените свои знания и возможности по каждому из разделов. В соответствии с этой оценкой на индивидуальных консультациях мы постараемся устранить имеющиеся пробелы.
Актуализация знаний учащихся
а) Показательные уравнения и неравенства и методы их решения (Приложение 1).
б) Логарифмические уравнения и неравенства и методы их решения (Приложение 2)
Комплексное применение знаний на практике.
1. Применение теоретического материала к решению задач.
Одновременно у доски работают двое учащихся. Один решает показательное уравнение и неравенство, второй логарифмическое уравнение и неравенство.
а) 
б) 
а) 49 x -8∙7 x + 7 = 0
б) 
1. Тестовая работа
Оцените свои умения решать простейшие показательные и логарифмические уравнения и неравенства. У каждого из вас есть индивидуальная карточка с тестовыми заданиями. Шесть заданий этого теста взяты из открытого банка заданий по математике (http://mathege.ru) и являются прототипами задания В3 ЕГЭ. Ответы записывайте в специальных полях и обращайте внимание на образец написания цифр. На выполнение теста отводим 15 минут. По окончании вы в соответствии оцениваете свою работу и выставляете соответствующую отметку в диагностическую карту.
Критерии оценивания: 8 заданий – «5»; 6,7 заданий – «4»; 4, 5 заданий – «3» и менее 4 заданий –«2».
В1. Найдите корень уравнения
В2. найдите корень уравнения
В3. Найдите корень уравнения
В4. Найдите корень уравнения
В5 Найдите корень уравнения
В6. Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них
Видео:Логарифмические уравнения. 11 класс.Скачать
Неравенства. Метод замены множителя (метод рационализации)
Полезный прием для решения сложных неравенств на ЕГЭ по математике – метод рационализации неравенства. Другое название — метод замены множителя. Это один из тех секретов, о которых ученику рассказывает репетитор. В учебниках о таком не написано.
Суть метода в том, чтобы от неравенства, содержащего в качестве множителей сложные показательные или логарифмические выражения, перейти к равносильному ему более простому рациональному неравенству.
Давайте для начала вспомним, что такое равносильные уравнения (или неравенства) В школьной программе этот важный вопрос почти не обсуждается. Поэтому запишем определение.
Равносильными называются уравнения, множества решений которых совпадают.
Заметим, что внешне уравнения могут быть и не похожи друг на друга.
Например, уравнения ( x − 3) 2 = 0 и x − 3 = 0 равносильны. Число 3 является единственным решением и того, и другого.
Уравнения 
и также равносильны. Оба они не имеют решений. Другими словами, множество решений каждого из них – пусто.
Уравнения и не являются равносильными. Решением первого уравнения является только x = 5. Решения второго – два числа: x = 5 и x = 1. Получается, что возведение обеих частей уравнения в квадрат в общем случае приводит к уравнению, неравносильному исходному.
Аналогичное определение – для неравенств.
Равносильными называются неравенства, множества решений которых совпадают.
Например, неравенства 0″ src=»https://latex.codecogs.com/png.latex?(x-1)(x-3)%3E0″ /> и 0″ src=»https://latex.codecogs.com/png.latex?%5Cfrac%3Cx-1%3E%3Cx-3%3E%3E0″ /> равносильны – ведь множества их решений совпадают. В этом легко убедиться с помощью метода интервалов.
Неравенства log_5″ src=»https://latex.codecogs.com/png.latex?log_%3C2%3Ex%3Elog_%3C2%3E5″ /> и 5″ src=»https://latex.codecogs.com/gif.latex?x%3E&space;5″ /> также равносильны при 0″ src=»https://latex.codecogs.com/gif.latex?x%3E&space;0″ />. Заметим, что внешне эти неравенства не похожи – одно из них логарифмическое, другое алгебраическое.
Другими словами, при x > 0 неравенства 0″ src=»https://latex.codecogs.com/png.latex?log_%3C2%3Ex-log_%3C2%3E5%3E0″ /> и 0″ src=»https://latex.codecogs.com/png.latex?x-5%3E0″ /> имеют одинаковые решения. Если какое-либо число x > 0 является решением одного из них, то оно будет и решением второго.
А это значит, что при любом x > 0 выражение будет иметь такой же знак, как и выражение x − 5. Следовательно, если в какое-либо сложное неравенство входит в качестве множителя выражение то при выполнении условия x > 0 его можно заменить на более простое x − 5 и получить неравенство, равносильное исходному.
Вот ключевой момент. На этом и основан метод рационализации – замены множителей, содержащих сложные логарифмические или показательные выражения, на более простые алгебраические множители.
Например, выражение вида , где f и g – функции от x, a – число, можно заменить на более простое ( f − g) ( a − 1) – конечно, при условии, что f(x) > 0 и g(x) > 0. Доказательство легко провести самостоятельно.
А сейчас – самое главное: волшебная таблица, позволяющая заменять сложные логарифмические (или показательные) множители в неравенствах на более простые. Эта таблица является ключом к задаче С3. Вот увидите, она выручит вас на ЕГЭ по математике:
| Сложный множитель | На что заменить |
| log h f − log h g | ( h − 1) ( f − g) |
| log h f − 1 | ( h − 1) ( f − h) |
| log h f | ( h − 1) ( f − 1) |
| h f − h g | ( h − 1) ( f − g) |
| h f − 1 | ( h − 1) · f |
| f h − g h | ( f − g) · h |
| f, g — функции от x. h — функция или число. | |
Конечно же, все выражения, которые содержат логарифмы, существуют при f, g, h > 0 и h ≠ 1.
Когда на ЕГЭ по математике вы применяете метод рационализации (замены множителя), — обязательно поясните, что вы им воспользовались. И не забудьте доказать соответствующую формулу. Иначе можно потерять балл.
Обратите внимание, что мы говорим о замене множителя в неравенствах вида 
Знак здесь может быть любой: >, ≥, ≤. Правая часть обязательно должна быть равна нулю. И заменяем мы именно множитель (а не слагаемое, например). Иначе ничего не получится.
Перейдем к практике – к решению задач из вариантов ЕГЭ по математике Профильного уровня.
1.
ОДЗ неравенства:
Применим метод рационализации. В соответствии с нашей таблицей, множитель заменим на (2 − x − 1)( x + 2 − 1). Множитель вида заменим на ( x + 3 − 1)(3 − x − 1). Таким образом, от логарифмического неравенства мы перешли к рациональному:
Решим его методом интервалов:
Ответ:
2.
Заметим, что выражение положительно при x ∈ ОДЗ. Умножим обе части неравенства на это выражение.
Упростим числитель правой части неравенства:
Поделим обе части неравенства на 5 x > 0:
Неравенство уже намного проще, чем исходное. Но основания степеней разные! Чтобы применить метод рационализации, нам придется представить 2 x − 1 в виде степени с основанием 3.
Неравенство примет вид:
Воспользуемся методом замены множителя. Множитель вида h f −h g можно заменить на ( h − 1) ( f − g). Да и логарифм в знаменателе можно заменить на выражение x + 1.
Оценим . Это необходимо сделать, чтобы правильно расставить точки на числовой прямой.
Ответ:
3.
Постараемся упростить это неравенство. Область допустимых значений
0;\ x+1neq 0. endright.» src=»https://latex.codecogs.com/png.latex?%5Cleft%5C%3C%5Cbegin%3Cmatrix%3E&space;x%3E0;%5C%5C&space;x+1%5Cneq&space;0.&space;%5Cend%3Cmatrix%3E%5Cright.» />Отсюда следует, что x > 0. Это хорошо, потому что при данных значениях x выражение x + 1 строго положительно, следовательно, мы можем умножить на него обе части неравенства. Да и на x 2 тоже можно умножить обе части неравенства, и тогда оно станет проще
Преобразуем числители выражений в левой и правой части и сделаем замену log2 x = t
Теперь обе части неравенства можно сократить на 5 t > 0.
Поскольку , выражение 2 t−1 можно записать как 3 ( t−1)·log32
Заметим, что log32 − 2 t. Решим его:
Итак, t ≥ 1 или t ≤ log32 − 2.
Вернемся к переменной x:
или
Ответ:
4. Еще одна задача из той же серии.
Запишем ОДЗ:
Умножим обе части неравенства на 0″ src=»https://latex.codecogs.com/png.latex?log%5E%3C2%3E_%3C2%3E32x%3E0″ />. Постараемся упростить числители выражений в левой и правой части.
Поделим обе части неравенства на 0.» src=»https://latex.codecogs.com/png.latex?2%5E%3Clog_%3C2%3E(4x)%3E%3E0.» />
Хорошо бы сделать замену. Пусть log2(4 x) = t. Тогда:
Неравенство примет вид:
Мы уже знаем, как представить число 7 в виде степени числа 2:
Применим метод рационализации.
Оценим
Применим в левой части неравенства формулу перехода к другому основанию
Последовательно применим метод замены множителя, то есть метод рационализации.
Напомним, что множитель log h f можно заменить на ( h-1)( f-1), а множитель (log h f — 1) — на ( h — 1)( f — h).
Поскольку 0″ src=»https://latex.codecogs.com/png.latex?(x+5)%5E%3C2%3E%3E0″ /> при x ∈ ОДЗ, а 0″ src=»https://latex.codecogs.com/png.latex?2x%5E%3C2%3E+10x+14%3E0″ /> > 0 при всех x, получим:
Ответ: x ∈ (-5; -3]
Посмотрим, чем поможет метод замены множителя в решении сложного показательного неравенства.
6. Решите неравенство:
Числитель дроби в левой части — однородное выражение, где каждое слагаемое имеет степень 2х. Поделим обе части неравенства на
Поскольку , поделим обе части неравенства на
Применяя метод рационализации, множитель вида заменяем на
Остается решить неравенство методом интервалов. Но как сравнить и ?
Что больше? Давайте представим как логарифм с основанием
7. Теперь логарифмическое неравенство. Обратите внимание, что здесь лучше всего записывать решение в виде цепочки равносильных переходов. И само неравенство, которое мы упрощаем, и область его допустимых значений мы записываем в одну систему. И решаем ее.
Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что
Используем также условия
Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,
Согласно методу замены множителя, выражение заменим
Решить ее легко.
8. А теперь неравенство с ловушкой. Мы надеемся, что вы помните — нельзя извлекать корень из неравенства.
Извлекать корень из неравенства нельзя! Можно перенести все в левую часть неравенства и разложить на множители как разность квадратов:
Применим формулы разности и суммы логарифмов, следя за областью допустимых значений. Все выражения под логарифмами в исходном неравенстве должны быть положительны.
Посмотрим на второе и третье неравенства системы. Поскольку х+5 положительно, то и выражение должно быть положительно.
Заметим, что решения неравенства — это все числа, кроме
По методу рационализации, каждый из множителей вида заменяем на
Просто равносильные преобразования. Выражение положительно всегда — так как в уравнении дискриминант отрицателен. Осталось применить метод интервалов.
Видео:11 класс, 12 урок, Показательные уравненияСкачать
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс Урок №44. Показательные и логарифмические уравнения и неравенства.
Перечень вопросов, рассматриваемых в теме
1) показательные уравнения и неравенства;
2) логарифмические уравнения и неравенства;
3) системы уравнений.
Глоссарий по теме
Показательными называются уравнения и неравенства, у которых переменная содержится в показатели степени.
Логарифмические уравнения и неравенства — это уравнения и неравенства, в которых переменная величина находится под знаком логарифма.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Вы уже умеете решать все виды уравнений и неравенств. Наша задача обобщить изученное, привести знания в систему. Начнем с показательных уравнений.
a х =b. где a>0, a≠1
Если b>0, уравнение имеет один корень: x=loga b. График функции y=a x пересекает прямую y=b в одной точке.
Если b≤0 корней нет. График функции y=a x не пересекает прямую y=b.
При решении неравенств, обращаем внимание на основание. Если а>0, знак неравенства сохраняется. Если а 0, a≠1.
Логарифмическое уравнение logax=b имеет один положительный корень x=a b при любом значении b.
График функции пересекает прямую y=b в одной точке.
Уравнение имеет один положительный корень x=a b при любом b. График функции у= logax пересекает прямую y=b в одной точке.
При решении логарифмических неравенств обращаем внимание на область допустимых значений. Затем с учетом ОДЗ и значения решаем неравенство.
Теперь рассмотрим методы решения. Основных приема два: приведение к одинаковому знаменателю и замена переменной.
1 прием. Как в показательном, так и в логарифмическом уравняем основания. Затем сравним показатели или числа, стоящие под знаком логарифма.
2 прием. Замена переменных.
Находим корни и делаем обратную замену. При решении неравенств применяем те же самые приемы.
При решении логарифмических уравнений, возможно появление посторонних корней. Причина их появления — расширение области определения исходного уравнения. Поэтому проверка корней логарифмического уравнения осуществляется либо по области определения, либо непосредственной подстановкой найденных корней в исходное логарифмическое уравнение.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Решить уравнение:
При х= -2 выражение lg(x-1) не имеет смысла, т.е. х=-2 посторонний корень. Ответ: х=2.
Пример 2. Найти значение выражения (х+у). x
Найдем область определения: х>0, у>0.
- lg(xy)=lg100 ↔ xy=100 ↔ 2xy=200
- сложим два уравнения: х 2 +2ху+у 2 =425+200=625 ↔ (х+у) 2 =625
🎬 Видео
11 класс, 18 урок, Логарифмические неравенстваСкачать
Показательные уравнения. 11 класс.Скачать
✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать
Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать
ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать
Проще простого! Как решить Логарифмическое Уравнение?Скачать
84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать
Это просто! Как решать Показательные Неравенства?Скачать
Решение логарифмических уравнений и неравенствСкачать
Решение логарифмических уравнений. Вебинар | МатематикаСкачать
Методы решения показательных уравнений. Урок №25.Скачать
Логарифмические неравенства. 11 класс.Скачать
Старт Щелчка. №14 Неравенства с нуля и до ЕГЭ за 5 часов | Логарифмы, степени для №5,6,12Скачать
Решение показательных уравнений и неравенствСкачать
Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать
