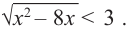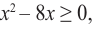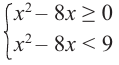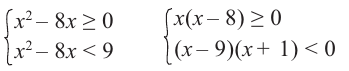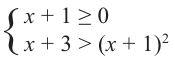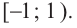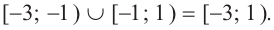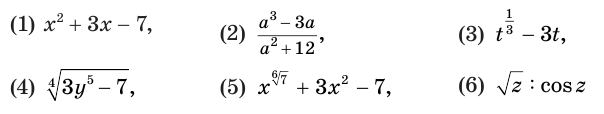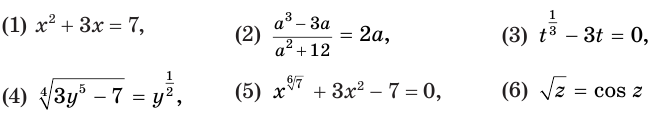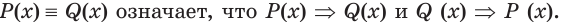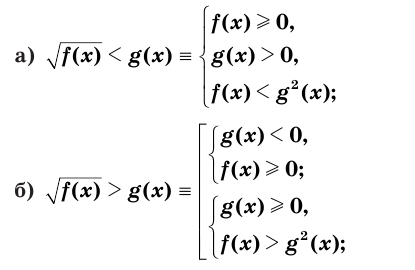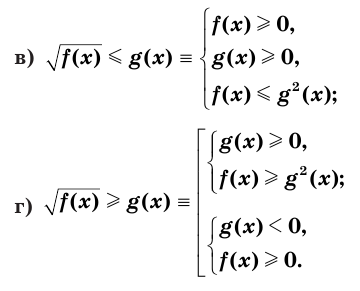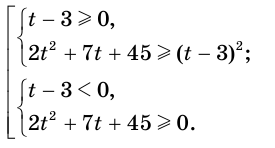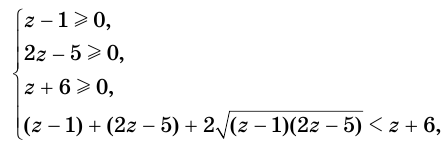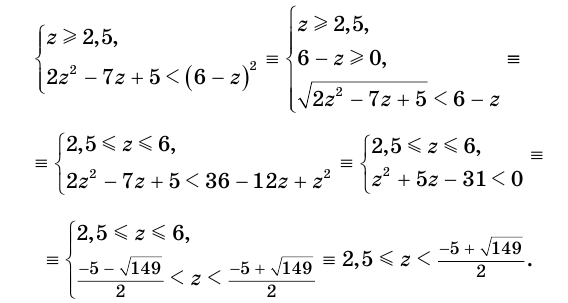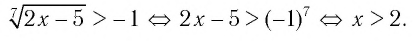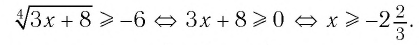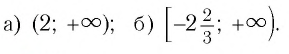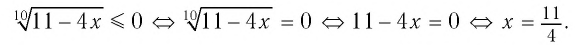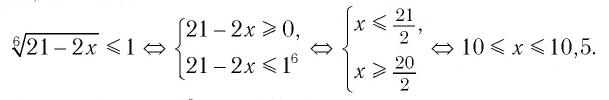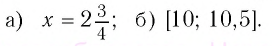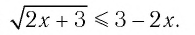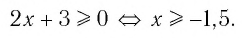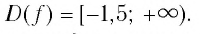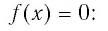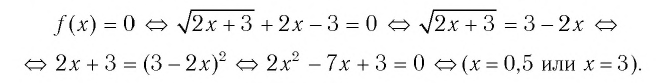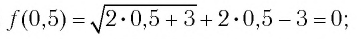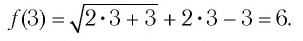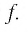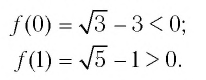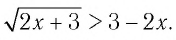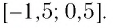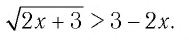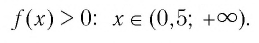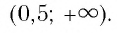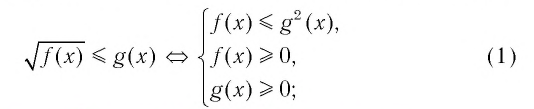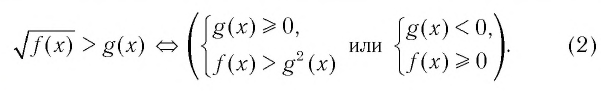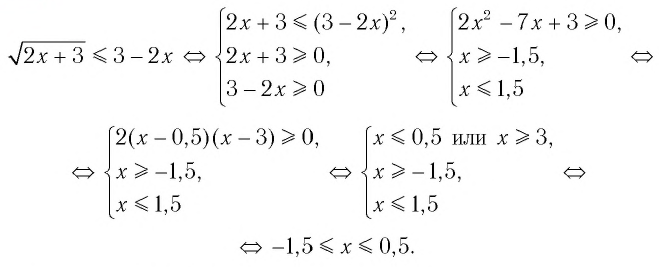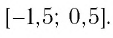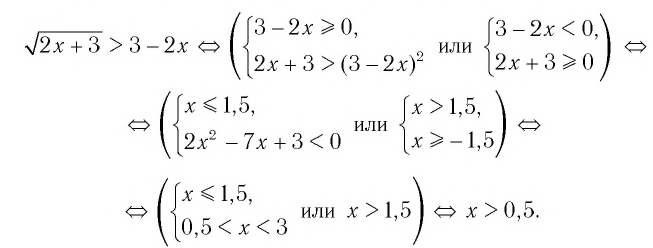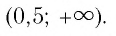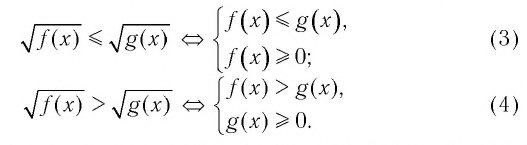- «Научные статьи, доклады, лекции, эссе преподавателей и студентов России»
- Основные методы решения иррациональных уравнений и неравенств
- Метод возведения в степень.
- Метод умножения на сопряженное выражение.
- Метод замены переменных.
- Метод выделения полных квадратов.
- Алгебра
- Иррациональные уравнения
- Простейшие иррациональные уравнения
- Уравнения с двумя квадратными корнями
- Введение новых переменных
- Замена иррационального уравнения системой
- Уравнения с «вложенными» радикалами
- Иррациональные неравенства
- Иррациональные неравенства с примерами решения
- Способы решения иррациональных неравенств
- Пример №1
- Пример №2
- Какие неравенства называются иррациональными
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- 🎥 Видео
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

«Научные статьи, доклады, лекции, эссе преподавателей и студентов России»
Видео:Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Основные методы решения иррациональных уравнений и неравенств
Основной подход к решению иррациональных уравнений и неравенств – это их рационализация, то есть приведение их к рациональным алгебраическим уравнениям и неравенствам. Но между процедурами решения иррациональных неравенств и иррациональных уравнений существует заметное различие. При решении иррациональных неравенств постоянно необходимо следить за тем, чтобы после каждого преобразования получалось неравенство эквивалентное исходному неравенству. Отсюда и получаем различные методы решения иррациональных уравнений и неравенств.
Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Метод возведения в степень.
Данный метод является одним из наиболее известных методов решения иррациональных выражений. При использовании данного метода, следует не забывать, что всякое уравнение и неравенство всегда можно возвести в нечетную степень, ведь это преобразование является равносильным. А если уравнение нужно возвести в четную степень, то в общем случае получается переход к следствию, что допустимо, если возможна проверка корней. Если же при решении проверка невозможна или крайне затруднительна по какой-либо причине (например, при решении неравенств и некоторых уравнений получается бесконечное число корней), то необходимо сохранять равносильность преобразований. Для этого перед каждым возведением в четную степень надо не забывать выписывать условия, при которых обе части уравнения будут неотрицательны. Если уравнение или неравенство содержит несколько радикалов, то для избавления от них придется несколько раз возводить в степень исходное уравнение или неравенство. В таком случае перед очередным возведением в степень используют прием уединения радикала. В общем виде данный метод можно записать так:
fx =gx ⟺ gx≥0,fx=g2x.
Для иррациональных неравенств метод возведения в степень будет выглядеть так:
Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Метод умножения на сопряженное выражение.
При использовании данного метода выражение, которое содержит радикал, одновременно умножается и делится на сопряженное к нему выражение. В результате такого преобразования иррациональность пропадает, и решение уравнения или неравенства значительно упрощается. Причем нельзя забывать о потере или приобретении лишних корней.
Пусть S – некоторое выражение, содержащее корни. Сопряженным множителем относительно S будет являться такое выражение Q, не равное тождественно нулю, а также такое, что произведение S∙Q не будет содержать корней.
Так для выражения S=nxp∙yq∙…∙zl, где p, q,…,l – натуральные числа, меньшие n, сопряженный множитель будет иметь вид
Q=nxn-p∙yn-q∙…∙zn-l , так как S∙Q=x∙у∙…∙z.
Для выражений вида S=x ±у (x,у≥0) сопряженный множитель
Q=x ∓у , так как S∙Q=x2- у2=x-у .
А для выражений вида S=3x±3у сопряженным множителем будет являться выражение вида
Q=3×2∓3xy+3у2 , так как S∙Q=3×3±3у3=x±у .
Для выражения вида S=nx-ny (x,e≥0, n∈N, n≥4) сопряженный множитель выглядит так
Q=nx n-1 +nxn-2у+…+пхуп-2+пуп-1 ,
так как S∙Q=nxn- nxn =x-у.
Выражение вида S=nx+n у имеет сопряженный множитель, который находится на основании формул сокращенного умножения
a2n+1+b2n+1=(a+b)(a2n-a2n-1b+…-ab2n-1+b2n. [14 с.228-229]
Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Метод замены переменных.
Рационализирующие подстановки. Данный метод позволяет преобразовать иррациональное уравнение (неравенство) к рациональному виду. В таком случае можно говорить о рационализации уравнений и неравенств. Этот метод обычно применяется, если в уравнении (неравенстве) неоднократно встречается некоторое выражение, зависящее от переменной. Тогда можно обозначить это выражение какой-нибудь новой буквой и решить задачу относительно новой переменной, а только потом найти исходную неизвестную. Зачастую некоторые иррациональные уравнения и неравенства удается решить только при помощи введения двух вспомогательных переменных и последующего перехода к рациональной системе. Иногда подходящей заменой переменной иррациональное уравнение или неравенство можно свести к тригонометрическому уравнению или неравенству. Наиболее распространенной является подстановка пах+b=t. [17 с.17]
Решение уравнений (неравенств) на отдельных промежутках ОДЗ. Учет ОДЗ. В некоторых случаях может возникнуть необходимость разбить ОДЗ уравнения (неравенства) на отдельные промежутки, а затем на каждом из них решать данную задачу. Такая ситуация может возникнуть при выполнении преобразований, которые связаны с необходимостью разбить корень из произведения двух чисел или выражений на произведение корней, или если необходимо внести какую-либо величину под знак корня четной степени.
аЬ=аЬ , если a≥0, b≥0;-a-b, если a≤0, b≤0.
ab=a2b, если a≥0;-a2b, если a≤0. [11 с.73]
Видео:ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА неравенства с корнемСкачать

Метод выделения полных квадратов.
Данный метод основан на применении формулы a2 =a. [11 с.74]
Классификация иррациональных уравнение и неравенств по методам их решения
Каждый из выявленных выше методов подходит для решения не всех иррациональных уравнений и неравенств. Поэтому имеет место классификация иррациональных уравнений (неравенств) по методам их решения.
Метод возведения в степень подходит для решения большинства распространенных видов иррациональных уравнений и неравенств. Для каждого из таких видов существует стандартная схема решения.
Уравнения вида fx =gx ⟺ gx≥0,fx=g2x.
Неравенства вида fx 0,fx2
Уравнения вида fx=g(x)⇔fx≥0 или gx≥0fx=gx.
fx≤g(x)⇔fx≥0 fx=gx; fx
Уравнения вида nf(x)=mgx⇔x ∈ОДЗnfxНОК (n,м)=mgxНОК (n,м).
Используя метод умножения на сопряженное можно решить практически любое иррациональное уравнение (неравенство). Главным условием является наличие в одной из частей иррационального уравнения (неравенства) выражения, содержащего радикал, к которому можно найти сопряженное отличное от нуля.
Для большинства подстановок необходимы какие-то условия или наличие некоторого выражения в составе уравнения (неравенства), которое можно заменить определенным образом.
Так уравнения вида пах+b±mcx+d=p (где a, b, с, d – некоторые числа, n, м – натуральные, которые обычно не превосходят 4) решаются обычно двойной подстановкой v=nax+b и и=мсх+d, благодаря которой получаем уравнение v+и=p.
Для таких тригонометрических подстановок как x=a sint, t∈-π2;π2 и x=a cost, t∈0;π необходимо наличие в уравнении или неравенстве радикала a2 -x2.
Для замены x=a tant, t∈-π2;π2 или x=acott, t∈0;π необходим радикал a2 +x2.
Если в иррациональном уравнении (неравенстве) присутствует радикал x2-a2, то можно говорить о подстановке вида x=asint, t∈-π2;π2 и x=acost, t∈0;π. [14 с.233-236]
Метод учета ОДЗ и решения задачи на отдельных промежутках ОДЗ не требует от иррациональных уравнений и неравенств определенных требований. Но, например, корни неравенства f(x)>-p можно найти, определив ОДЗ, так как левая часть неравенства всегда больше правой.
Для метода выделения полных квадратов необходимо чтобы под знаком одного радикала второй степени находились две переменные или два выражения, содержащие неизвестную, степени которых различаются в два раза. Например, в уравнении вида x2+2ax+a2-x+b2-2bx=p под знаками радикала можно выделить полные квадраты выражений и использовать формулу a2 =a, и в результате получится следующее уравнение x+a-x-b=p.
Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Алгебра
План урока:
Видео:Как решать иррациональные уравнения. Методы решения иррациональных уравнений. (часть 1).Скачать

Иррациональные уравнения
Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.
Приведем примеры иррациональных ур-ний:
Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.
Видео:Иррациональные неравенства | Математика ЕГЭ | УмскулСкачать

Простейшие иррациональные уравнения
Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:
где а – некоторое число (константа), f(x) – рациональное выражение.
Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:
Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии
n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.
Ответ: корней нет.
Пример. Решите ур-ние
Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:
Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).
Пример. Найдите решение ур-ния
Решение. Возведем обе части в пятую степень:
х 2 – 14х – 32 = 0
Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:
D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324
Итак, нашли два корня: (– 2) и 16.
Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.
Пример. Решите ур-ние
Решение. Возводим обе части во вторую степень:
х – 2 = х 2 – 8х + 16
D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9
Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):
при х = 3 х – 4 = 3 – 4 = – 1
при х = 6 6 – 4 = 6 – 4 = 2
Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.
Пример. Решите ур-ние
Решение. Здесь используется кубический корень, а потому возведем обе части в куб:
3х 2 + 6х – 25 = (1 – х) 3
3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3
Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:
Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.
Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:
при х = 2 1 – х = 1 – 2 = – 1
Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:
Видео:Решение неравенства методом интерваловСкачать

Уравнения с двумя квадратными корнями
Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.
Пример. Решите ур-ние
Решение. Перенесем вправо один из корней:
Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:
Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:
Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:
(2х – 4) 2 = 13 – 3х
4х 2 – 16х + 16 = 13 – 3х
4х 2 – 13х + 3 = 0
D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121
Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:
Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3
На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.
Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Введение новых переменных
Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние
Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.
Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:
х 1/2 – 10х 1/4 + 9 = 0
Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид
Это квадратное ур-ние. Найдем его корни:
D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64
Получили два значения t. Произведем обратную замену:
х 1/4 = 1 или х 1/4 = 9
Возведем оба ур-ния в четвертую степень:
(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4
х = 1 или х = 6561
Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:
В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.
Пример. Решите ур-ние
х 1/3 + 5х 1/6 – 24 = 0
Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:
Его корни вычислим через дискриминант:
D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121
Далее проводим обратную заменуx 1/6 = t:
х 1/6 = – 8 или х 1/6 = 3
Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.
Видео:Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Замена иррационального уравнения системой
Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите ур-ние
Решение. Заменим первый корень буквой u, а второй – буквой v:
Исходное ур-ние примет вид
Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:
Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:
Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:
(х + 6) + (11 – х) = u 3 + v 2
из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:
17 = u 3 + (5 – u) 2
17 = u 3 + u 2 – 10u + 25
u 3 + u 2 – 10u + 8 = 0
Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа
подставим полученные значения в (4):
x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3
x + 6 = 1 или х + 6 = 8 или х + 6 = – 64
х = – 5 или х = 2 или х = – 70
Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим
Корень подошел. Проверяем следующее число, х = 2:
Корень снова оказался верным. Осталась последняя проверка, для х = – 70:
Итак, все три числа прошли проверку.
Видео:методы решения иррациональных уравнений и неравенствСкачать

Уравнения с «вложенными» радикалами
Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:
При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:
Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:
Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:
Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:
Возводим в квадрат и получаем:
х 2 + 40 = (х + 4) 2
х 2 + 40 = х 2 + 8х + 16
И снова нелишней будет проверка полученного корня:
Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Иррациональные неравенства
По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:
Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.
Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида
Может быть справедливым только тогда, когда
То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во
при четном n можно заменить системой нер-в
Пример. При каких значениях x справедливо нер-во
Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:
х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)
Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во
чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.
Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.
Пример. Найдите решение нер-ва
Решение. Всё очень просто – надо всего лишь возвести обе части в куб:
x 2 – 7x– 8 2 – 7x– 8 = 0
D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81
Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:
Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.
Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.
Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид
Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.
Пример. Решите нер-во
Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):
И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:
D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9
Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.
стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:
f(x) > 0 (подкоренное выражение не может быть отрицательным);
g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).
Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.
Пример. Решите нер-во
Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим
х 2 – 10х + 21 > 0(1)
Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:
Во-вторых, выражение 4 – х не может быть отрицательным:
Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):
Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:
Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:
Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:
Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:
Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).
Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Иррациональные неравенства с примерами решения
Неравенства, содержащие переменную под знаком радикала, называются иррациональными неравенствами.
Содержание:
Решение иррациональных неравенств также ищут на множестве действительных чисел и, используя свойства корня и неравенств, сводится к решению системы рациональных неравенств.
Пример: Решите неравенство
Решение: чтобы найти множество решений данного неравенства на множестве допустимых значений, т. е. при условии
Каждое неравенство системы решим методом интервалов и найдем пересечение полученных решений:
Пример: Решите неравенство
Решение: рассмотрим два случая, в зависимости от знака правой части.
1) при 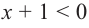
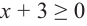
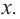
Ее решением является промежуток
2) при 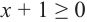
Ее решением является промежуток
Решением заданного неравенства является
Видео:Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

Способы решения иррациональных неравенств
С действием возведения в степень связаны разные виды выражений. Будем рассматривать выражения с переменными, при образовании которых используются действия сложения, вычитания, умножения, деления и возведения в степень, причем возведение в степень хотя бы один раз применено к выражению с переменной.
Если показатель степени целый, то возникает рациональное выражение, если дробный, то — иррациональное выражение, а если иррациональный, то — трансцендентное выражение.
К трансцендентным выражениям приводят и действия нахождения значений синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса, арккотангенса. Рациональные и иррациональные выражения вместе составляют множество алгебраических выражений.
выражения (1) и (2) являются рациональными, выражения (3) и (4) — иррациональными, выражения (5) и (6) — трансцендентными, а выражения (1)—(4) — алгебраическими.
В зависимости от того, из каких выражений составлено уравнение, говорят о рациональных, иррациональных, трансцендентных уравнениях.
уравнения (1) и (2) являются рациональными, уравнения (3) и (4) — иррациональными, а уравнения (5) и (6) — трансцендентными.
Так же говорят о рациональных, иррациональных, трансцендентных неравенствах.
В этом параграфе рассматривается решение иррациональных уравнений и неравенств. При их решении нужно следить за тем, какие преобразования выполняются при этом.
Утверждение 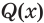
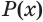
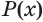
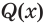
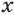
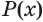
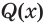
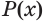
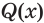
Утверждение 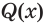
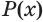
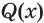
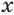
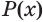
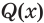

Отношения равносильности и следования связаны:
При решении иррациональных неравенств нужно учитывать, что проверка подстановкой найденного множества чисел обычно невозможна из-за его бесконечности. Поэтому при решении неравенств нужно следить за равносильностью проводимых преобразований.
Теорема:
Верны следующие равносильности:
Доказательство проводится по схеме, использованной при доказательстве теоремы 9 с применением соответствующих свойств числовых неравенств.
Пример №1
Решим неравенство 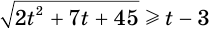
Первую систему можно заменить равносильной системой 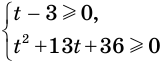


Вторая система совокупности равносильна системе 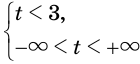
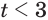
Решения данного неравенства получим, когда объединим решения 
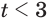
Ответ. 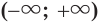
Пример №2
Решим неравенство 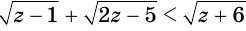
Обратим внимание на то, что на области определения левая и правая части данного неравенства обе неотрицательны, поэтому оно равносильно системе неравенств
решение которой следующее:
Ответ. 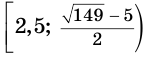
Видео:9 класс, 6 урок, Иррациональные неравенстваСкачать

Какие неравенства называются иррациональными
В этой лекции мы будем рассматривать неравенства, содержащие переменную (неизвестное) под знаком корня. Такие неравенства называются иррациональными.
При решении иррациональных неравенств часто используют подход, который мы уже применяли, решая иррациональные уравнения. Он состоит в замене исходного неравенства равносильным ему неравенством (системой или совокупностью неравенств).
Пример №3
Решение:
а) Учитывая свойства корня нечетной степени, получаем:
б) По определению корня четной степени значения выражения
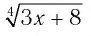
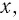
выражение имеет смысл, т. е. когда значения подкоренного выражения неотрицательны. Таким образом, имеем:
Ответ:
Пример №4
Решение:
а) По определению корня четной степени значения выражения 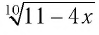
б) Поскольку обе части неравенства 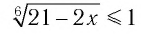
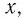
Ответ:
При решении иррациональных неравенств часто используется также метод интервалов.
Пример №5
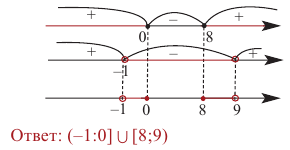
Решить неравенство
Решение:
Обозначим 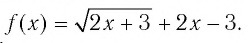
Таким образом,
Найдем нули функции 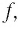
Проверка:
Значит, 0,5 — единственный нуль функции
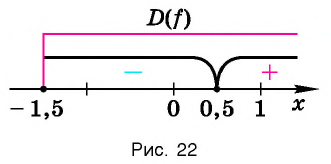
Отметим нуль функции 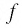
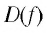
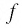
Используя рисунок 22, запишем решение неравенства
Ответ:
Пример №6
Решить неравенство
Решение:
Решение этого примера аналогично решению примера 3.
Используя рисунок 22, записываем решение неравенства
Ответ:
▲ При решении иррациональных неравенств часто используются следующие утверждения о равносильности неравенств и систем неравенств:
Решим пример 3, используя равносильность (1):
Ответ:
Решим пример 4, используя равносильность (2):
Ответ:
Для решения заданий такого типа, как, например, в 1.265, можно использовать следующие утверждения о равносильности:
Аналогичные утверждения можно записать и для неравенств
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Производная в математике
- Как найти производную функции
- Асимптоты графика функции
- Касательная к графику функции и производная
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)
- Иррациональные уравнения
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎥 Видео
Иррациональные неравенства. 11 класс.Скачать

Методы решения иррациональных неравенств и уравнений с примерамиСкачать