Основные кинематические характеристики и уравнения поступательного движения абсолютно твердого тела

лЙОЕНБФЙЛБ ЙЪХЮБЕФ ТБЪМЙЮОЩЕ НЕИБОЙЮЕУЛЙЕ ДЧЙЦЕОЙС ФЕМ ВЕЪ ТБУУНПФТЕОЙС РТЙЮЙО ЧЩЪЩЧБАЭЙИ ЬФЙ ДЧЙЦЕОЙС.

1.1.1 лЙОЕНБФЙЛБ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС

рТЙ РПУФХРБФЕМШОПН ДЧЙЦЕОЙЙ ФЕМБ ЧУЕ ФПЮЛЙ ФЕМБ ДЧЙЦХФУС ПДЙОБЛПЧП, Й, ЧНЕУФП ФПЗП ЮФПВЩ ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ЛБЦДПК ФПЮЛЙ ФЕМБ, НПЦОП ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ФПМШЛП ПДОПК ЕЗП ФПЮЛЙ.

пУОПЧОЩЕ ИБТБЛФЕТЙУФЙЛЙ ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ: ФТБЕЛФПТЙС ДЧЙЦЕОЙС, РЕТЕНЕЭЕОЙЕ ФПЮЛЙ, РТПКДЕООЩК ЕА РХФШ, ЛППТДЙОБФЩ, УЛПТПУФШ Й ХУЛПТЕОЙЕ.

мЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ Ч РТПУФТБОУФЧЕ, ОБЪЩЧБАФ ФТБЕЛФПТЙЕК.

рЕТЕНЕЭЕОЙЕН НБФЕТЙБМШОПК ФПЮЛЙ ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ОБЪЩЧБЕФУС ЧЕЛФПТ РЕТЕНЕЭЕОЙС &#8710r=r-r₀, ОБРТБЧМЕООЩК ПФ РПМПЦЕОЙС ФПЮЛЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ Л ЕЕ РПМПЦЕОЙА Ч ЛПОЕЮОЩК НПНЕОФ.

уЛПТПУФШ НБФЕТЙБМШОПК ФПЮЛЙ РТЕДУФБЧМСЕФ УПВПК ЧЕЛФПТ, ИБТБЛФЕТЙЪХАЭЙК ОБРТБЧМЕОЙЕ Й ВЩУФТПФХ РЕТЕНЕЭЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ. чЕЛФПТ ХУЛПТЕОЙС ИБТБЛФЕТЙЪХЕФ ВЩУФТПФХ Й ОБРТБЧМЕОЙЕ ЙЪНЕОЕОЙС УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ.

1.1.2 тБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ

тБЧОПНЕТОЩН РТСНПМЙОЕКОЩН ДЧЙЦЕОЙЕН ОБЪЩЧБЕФУС ФБЛПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН НБФЕТЙБМШОБС ФПЮЛБ (ФЕМП) ДЧЙЦЕФУС РП РТСНПК Й Ч МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ УПЧЕТЫБЕФ ПДЙОБЛПЧЩЕ РЕТЕНЕЭЕОЙС.

чЕЛФПТ УЛПТПУФЙ ТБЧОПНЕТОПЗП РТСНПМЙОЕКОПЗП ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ОБРТБЧМЕО ЧДПМШ ЕЕ ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС. чЕЛФПТ УЛПТПУФЙ РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧЕО ЧЕЛФПТХ РЕТЕНЕЭЕОЙС ЪБ МАВПК РТПНЕЦХФПЛ ЧТЕНЕОЙ, РПДЕМЕООПНХ ОБ ЬФПФ РТПНЕЦХФПЛ ЧТЕНЕОЙ:

рТЙНЕН МЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ, ЪБ ПУШ ЛППТДЙОБФ пи, РТЙЮЕН ЪБ РПМПЦЙФЕМШОПЕ ОБРТБЧМЕОЙЕ ПУЙ ЧЩВЕТЕН ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФПЮЛЙ. фПЗДБ, УРТПЕГЙТПЧБЧ ЧЕЛФПТЩ r Й v, ОБ ЬФХ ПУШ, ДМС РТПЕЛГЙК ∆r_x = |∆r| Й ∆v_x = |∆v| ЬФЙИ ЧЕЛФПТПЧ НЩ НПЦЕН ЪБРЙУБФШ:

, ПФУАДБ РПМХЮБЕН ХТБЧОЕОЙЕ ТБЧОПНЕТОПЗП ДЧЙЦЕОЙС: ∆r_x = v_x · t .

ф.Л. РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ S = |∆r|, НПЦЕН ЪБРЙУБФШ: S_x = v_x · t. фПЗДБ ДМС ЛППТДЙОБФЩ ФЕМБ Ч МАВПК НПНЕОФ ЧТЕНЕОЙ ЙНЕЕН:

ЗДЕ И₀ — ЛППТДЙОБФБ ФЕМБ Ч ОБЮБМШОЩК НПНЕОФ t = 0.

рТЙНЕТ 1. хТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ДБОП Ч ЧЙДЕ И = 4 — 3t. пРТЕДЕМЙФШ ОБЮБМШОХА ЛППТДЙОБФХ ФЕМБ, УЛПТПУФШ ДЧЙЦЕОЙС Й РЕТЕНЕЭЕОЙС ФЕМБ ЪБ 2 УЕЛХОДЩ.

тЕЫЕОЙЕ: уТБЧОЙН ДБООПЕ ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ У ХТБЧОЕОЙЕН ДЧЙЦЕОЙС Ч ПВЭЕН ЧЙДЕ: И = И₀ + v_x t Й И = 4 — 3t.

пЮЕЧЙДОП, ЮФП И₀ = 4Н, v_x = — 3Н/У (ЪОБЛ «-» ПЪОБЮБЕФ, ЮФП ОБРТБЧМЕОЙЕ УЛПТПУФЙ ОЕ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ПУЙ пи, Ф.Е. ПОЙ РТПФЙЧПРПМПЦОП ОБРТБЧМЕОЩ). рЕТЕНЕЭЕОЙЕ ФЕМБ ОБКДЕН РП ЖПТНХМЕ: S = И — И₀. лПОЕЮОХА ЛППТДЙОБФХ И НПЦОП ПРТЕДЕМЙФШ, РПДУФБЧМСС Ч ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЧТЕНС t₁: И = 4 — 3t₁. ч ПВЭЕН ЧЙДЕ ЖПТНХМБ РЕТЕНЕЭЕОЙС: S = 4 — 3t₁ — И₀ = 4 — 3t₁ — 4 = — 3t₁ = -3 · 2 = — 6 Н (фЕМП ДЧЙЦЕФУС Ч ПФТЙГБФЕМШОПН ОБРТБЧМЕОЙЙ ПУЙ пи).

рТЙНЕТ 2.мПДПЮОЙЛ РЕТЕЧПЪЙФ РБУУБЦЙТПЧ У ПДОПЗП ВЕТЕЗБ ОБ ДТХЗПК ЪБ ЧТЕНС t =10 НЙО. РП ФТБЕЛФПТЙЙ бч. уЛПТПУФШ ФЕЮЕОЙС ТЕЛЙ vТ = 0,3 Н/У, ЫЙТЙОБ ТЕЛЙ 240 Н. у ЛБЛПК УЛПТПУФША v ПФОПУЙФЕМШОП ЧПДЩ Й РПД ЛБЛЙН ХЗМПН α Л ВЕТЕЗХ ДПМЦОБ ДЧЙЗБФШУС МПДЛБ, ЮФПВЩ ДПУФЙЮШ ДТХЗПЗП ВЕТЕЗБ ЪБ ХЛБЪБООПЕ ЧТЕНС?

t = 10 НЙО = 660 У.

v’ — ? α — ?

тЕЫЕОЙЕ: рТЙНЕН ВЕТЕЗ ЪБ ОЕРПДЧЙЦОХА УЙУФЕНХ ПФУЮЕФБ. фПЗДБ ПФОПУЙФЕМШОП ВЕТЕЗБ УЛПТПУФШ МПДЛЙ ТБЧОБ:

ьФБ УЛПТПУФШ (ТЙУХОПЛ 1.1), СЧМСЕФУС УХННПК ДЧХИ УЛПТПУФЕК: УЛПТПУФЙ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ v’ (УЛПТПУФЙ ПФОПУЙФЕМШОП РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ) Й УЛПТПУФЙ ТЕЛЙ v_Т (УЛПТПУФЙ УБНПК РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ ПФОПУЙФЕМШОП ОЕРПДЧЙЦОПК). рП ЪБЛПОХ УМПЦЕОЙС УЛПТПУФЕК: v =v_Т + v’. фБЛ ЛБЛ РП ХУМПЧЙА ЪБДБЮЙ УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ВЕТЕЗБ ОБРТБЧМЕОБ ЧДПМШ бч, Б УЛПТПУФШ ТЕЛЙ РЕТРЕОДЙЛХМСТОП бч, ФП УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ(РП ФЕПТЕНЕ рЙЖБЗПТБ):

йУЛПНЩК ХЗПМ НПЦОП ОБКФЙ ЙЪ ЧЩТБЦЕОЙС:

пФЧЕФ: v’ = 0.5 Н /У, α = arctg ≈ 53 0 .

1.1.3 оЕТБЧОПНЕТОПЕ ДЧЙЦЕОЙЕ

дЧЙЦЕОЙЕ, РТЙ ЛПФПТПН ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ФЕМП УПЧЕТЫБЕФ ОЕТБЧОЩЕ РЕТЕНЕЭЕОЙС ОБЪЩЧБАФ ОЕТБЧОПНЕТОЩН ЙМЙ РЕТЕНЕООЩН. уТЕДОЕК УЛПТПУФША v_УТ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА РЕТЕНЕЭЕОЙС ФЕМБ ∆r ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ЬФПНХ РТПНЕЦХФЛХ:

нПДХМШ УТЕДОЕК УЛПТПУФЙ ПРТЕДЕМСЕФУС ЛБЛ ПФОПЫЕОЙЕ РХФЙ ∆S, РТПКДЕООПЗП ФЕМПН ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ, Л ЬФПНХ РТПНЕЦХФЛХ:

оБРТБЧМЕОЙЕ ЧЕЛФПТБ УТЕДОЕК УЛПТПУФЙ v_УТ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ∆r (ТЙУХОПЛ 1.2).

рТЙ ОЕПЗТБОЙЮЕООПН ХНЕОШЫЕОЙЙ ∆t, v_УТ УФТЕНЙФУС Л РТЕДЕМШОПНХ ЪОБЮЕОЙА, ЛПФПТПЕ ОБЪЩЧБЕФУС НЗОПЧЕООПК УЛПТПУФША. йФБЛ, НЗОПЧЕООБС УЛПТПУФШ v ЕУФШ РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС УЛПТПУФШ v_УТ, ЛПЗДБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ДЧЙЦЕОЙС УФТЕНЙФУС Л ОХМА:

йЪ ЛХТУБ НБФЕНБФЙЛЙ ЙЪЧЕУФОП, ЮФП РТЕДЕМ ПФОПЫЕОЙС РТЙТБЭЕОЙС ЖХОЛГЙЙ Л РТЙТБЭЕОЙА БТЗХНЕОФБ, ЛПЗДБ РПУМЕДОЙК УФТЕНЙФУС Л ОХМА РТЕДУФБЧМСЕФ УПВПК РЕТЧХА РТПЙЪЧПДОХА ЬФПК ЖХОЛГЙЙ РП ДБООПНХ БТЗХНЕОФХ. рПЬФПНХ:

нЗОПЧЕООБС УЛПТПУФШ v ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК ТБДЙХУБ — ЧЕЛФПТБ ДЧЙЦХЭЕКУС ФПЮЛЙ РП ЧТЕНЕОЙ. фБЛ ЛБЛ УЕЛХЭБС Ч РТЕДЕМЕ УПЧРБДБЕФ У ЛБУБФЕМШОПК, ФП ЧЕЛФПТ УЛПТПУФЙ v ОБРТБЧМЕО РП ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС (ТЙУХОПЛ 1.2).

рП НЕТЕ ХНЕОШЫЕОЙЕ ∆t РХФШ ∆S ЧУЕ ВПМШЫЕ ВХДЕФ РТЙВМЙЦБФШУС Л |∆r|, РПЬФПНХ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ:

фБЛЙН ПВТБЪПН, НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ v ТБЧЕО РЕТЧПК РТПЙЪЧПДОПК РХФЙ РП ЧТЕНЕОЙ :

рТЙ ОЕТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФЕМБ ЕЗП УЛПТПУФШ ОЕРТЕТЩЧОП ЙЪНЕОСЕФУС. лБЛ ВЩУФТП ЙЪНЕОСЕФУС УЛПТПУФШ ФЕМБ, РПЛБЪЩЧБЕФ ЧЕМЙЮЙОБ, ЛПФПТБС ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН. уТЕДОЙН ХУЛПТЕОЙЕН ОЕТБЧОПНЕТОПЗП ДЧЙЦЕОЙС Ч ЙОФЕТЧБМЕ ПФ t ДП t + ∆t ОБЪЩЧБЕФУС ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС УЛПТПУФЙ ∆v Л ЙОФЕТЧБМХ ЧТЕНЕОЙ ∆t:

нЗОПЧЕООЩН ХУЛПТЕОЙЕН Б Ч НПНЕОФ ЧТЕНЕОЙ t ВХДЕФ РТЕДЕМ УТЕДОЕЗП ХУЛПТЕОЙС:

фБЛЙН ПВТБЪПН, ХУЛПТЕОЙЕ ∆Б ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК УЛПТПУФЙ РП ЧТЕНЕОЙ. ч ДБООПК УЙУФЕНЕ ПФУЮЕФБ ЧЕЛФПТ ХУЛПТЕОЙС НПЦЕФ ВЩФШ ЪБДБО РТПЕЛГЙСНЙ ОБ УППФЧЕФУФЧХАЭЙЕ ЛППТДЙОБФОЩЕ ПУЙ (РТПЕЛГЙСНЙ Б_И, Б_Х, Б_z).

уПУФБЧМСАЭБС Б_τ ЧЕЛФПТБ ХУЛПТЕОЙС, ОБРТБЧМЕООБС ЧДПМШ ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч ДБООПК ФПЮЛЕ, ОБЪЩЧБЕФУС ФБОЗЕОГЙБМШОЩН (ЛБУБФЕМШОЩН) ХУЛПТЕОЙЕН. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ ИБТБЛФЕТЙЪХЕФ ЙЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ РП НПДХМА. чЕЛФПТ Б_τ ОБРТБЧМЕО Ч УФПТПОХ ДЧЙЦЕОЙС ФПЮЛЙ РТЙ ЧПЪТБУФБОЙЙ ЕЕ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — Б) Й Ч РТПФЙЧПРПМПЦОХА УФПТПОХ — РТЙ ХВЩЧБОЙЙ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — В).

фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС Б_τ ТБЧОБ РЕТЧПК РТПЙЪЧПДОПК РП ЧТЕНЕОЙ ПФ НПДХМС УЛПТПУФЙ, ПРТЕДЕМСС ФЕН УБНЩН ВЩУФТПФХ ЙЪНЕОЕОЙС УЛПТПУФЙ РП НПДХМА:

чФПТБС УПУФБЧМСАЭБС ХУЛПТЕОЙС, ТБЧОБС:

ОБЪЩЧБЕФУС ОПТНБМШОПК УПУФБЧМСАЭЕК ХУЛПТЕОЙС Й ОБРТБЧМЕОБ РП ОПТНБМЙ Л ФТБЕЛФПТЙЙ Л ГЕОФТХ ЕЕ ЛТЙЧЙЪОЩ (РПЬФПНХ ЕЕ ОБЪЩЧБАФ ФБЛ ЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН).

рПМОПЕ ХУЛПТЕОЙЕ ЕУФШ ЗЕПНЕФТЙЮЕУЛБС УХННБ ФБОЗЕОГЙБМШОПК Й ОПТНБМШОПК УПУФБЧМСАЭЙИ:

рТЙНЕТ 1. рХУФШ И ЧПЪТБУФБЕФ РТПРПТГЙПОБМШОП ЛЧБДТБФХ ЧТЕНЕОЙ, Ф.Е. И = б·t 2 . юЕНХ ТБЧОБ НЗОПЧЕООБС УЛПТПУФШ Ч НПНЕОФ ЧТЕНЕОЙ t₁ — ?

тЕЫЕОЙЕ: ч ПВЭЕН УМХЮБЕ РТПЙЪЧПДОБС ПФ УФЕРЕООПК ЖХОЛГЙЙ t n ЪБРЙУЩЧБЕФУС Ч ЧЙДЕ:

нЗОПЧЕООБС УЛПТПУФШ ПРТЕДЕМСЕФУС:

пФЧЕФ: ч НПНЕОФ ЧТЕНЕОЙ t₁ ЙНЕЕН v = 2·Б·t₁.

рТЙНЕТ 2. ъБЧЙУЙНПУФШ РТПКДЕООПЗП ФЕМПН РХФЙ S ПФ ЧТЕНЕОЙ t ЪБДБЕФУС ХТБЧОЕОЙЕН S = At — Bt 2 + Ct 3 , ЗДЕ б = 2 Н/У, ч = 3 Н/У 2 , у = 4 Н/У 3 .

оБКФЙ: Б) ЪБЧЙУЙНПУФШ УЛПТПУФЙ v Й ХУЛПТЕОЙС a ФЕМБ ПФ ЧТЕНЕОЙ t;

В) ТБУУФПСОЙЕ S, УЛПТПУФШ v Й ХУЛПТЕОЙЕ Б ФЕМБ ЮЕТЕЪ ЧТЕНС t =2 У РПУМЕ ОБЮБМБ ДЧЙЦЕОЙС.

S = At — Bt 2 + Ct 3 , б = 2 Н/У, ч = 3 Н/У 2 , у = 4 Н/У 3 ;

В) S -? , V -? , a-? РТЙ t = 2 c.

Б) уЛПТПУФШ ФЕМБ: v = ds /dt ; v = A — 2Bt + 3Ct 2 ; v = 2 — 6t + 12t 2 Н/У. хУЛПТЕОЙЕ ФЕМБ: Б = dv /dt; Б= — 2B + 6уt; a = — 6 + 24t Н/У 2 .

В) тБУУФПСОЙЕ, РТПКДЕООПЕ ФЕМПН, S = 2t — 3t 2 + 4t 3 . фПЗДБ ЮЕТЕЪ ЧТЕНС t = 2c ЙНЕЕН: S = 24 Н; v = 38 Н/У; Б = 42 Н/У 2 .

пФЧЕФ: v = 2 — 6t + 12t 2 ; a = — 6 + 24 t Н/У 2 ; S = 24 Н; v = 38 Н/У; Б = 42 Н/У 2 .

1.1.4 тБЧОПРЕТЕНЕООПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ

тБЧОПРЕТЕНЕООЩН ОБЪЩЧБЕФУС ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН УЛПТПУФШ ФЕМБ (НБФЕТЙБМШОПК ФПЮЛЙ) ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП, Ф.Е. ОБ ТБЧОЩЕ ЧЕМЙЮЙОЩ. ьФП ДЧЙЦЕОЙЕ НПЦЕФ ВЩФШ ТБЧОПХУЛПТЕООЩН Й ТБЧОПЪБНЕДМЕООЩН.

еУМЙ ОБРТБЧМЕОЙЕ ХУЛПТЕОЙС Б УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН УЛПТПУФЙ v ФПЮЛЙ, ДЧЙЦЕОЙЕ ОБЪЩЧБЕФУС ТБЧОПХУЛПТЕООЩН. еУМЙ ОБРТБЧМЕОЙЕ ЧЕЛФПТПЧ Б Й v РТПФЙЧПРПМПЦОЩ, ДЧЙЦЕОЙЕ ОБЪЩЧБЕФУС ТБЧОПЪБНЕДМЕООЩН.

рТЙ ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ХУЛПТЕОЙЕ ПУФБЕФУС РПУФПСООЩН Й РП НПДХМА Й РП ОБРТБЧМЕОЙА (Б = const). рТЙ ЬФПН УТЕДОЕЕ ХУЛПТЕОЙЕ Б_УТ ТБЧОП НЗОПЧЕООПНХ ХУЛПТЕОЙА Б ЧДПМШ ФТБЕЛФПТЙЙ ФПЮЛЙ. оПТНБМШОПЕ ХУЛПТЕОЙЕ РТЙ ЬФПН ПФУХФУФЧХЕФ ( Б_n=0 ).

йЪНЕОЕОЙЕ УЛПТПУФЙ ∆v = v — v₀ Ч ФЕЮЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t = t — t₀ РТЙ ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧОП: ∆v = a·∆t, ЙМЙ v — v₀ = a·(t — t₀). еУМЙ Ч НПНЕОФ ОБЮБМБ ПФУЮЕФБ ЧТЕНЕОЙ (t₀) УЛПТПУФШ ФПЮЛЙ ТБЧОБ v₀ (ОБЮБМШОБС УЛПТПУФШ) Й ХУЛПТЕОЙЕ Б ЙЪЧЕУФОП, ФП УЛПТПУФШ v Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t: v = v₀ + a·t. рТПЕЛГЙС ЧЕЛФПТБ УЛПТПУФЙ ОБ ПУШ пи УЧСЪБОБ У УППФЧЕФУФЧХАЭЙНЙ РТПЕЛГЙСНЙ ЧЕЛФПТПЧ ОБЮБМШОПК УЛПТПУФЙ Й ХУЛПТЕОЙС ХТБЧОЕОЙЕН: v_И = v_0И ± a_И·t. бОБМПЗЙЮОП ЪБРЙУЩЧБАФУС ХТБЧОЕОЙС ДМС РТПЕЛГЙК ЧЕЛФПТБ УЛПТПУФЙ ОБ ДТХЗЙЕ ЛППТДЙОБФОЩЕ ПУЙ.

чЕЛФПТ РЕТЕНЕЭЕОЙС ∆r ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀ РТЙ ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v₀ Й ХУЛПТЕОЙЕН Б ТБЧЕО:

Б ЕЗП РТПЕЛГЙС ОБ ПУШ пи (ЙМЙ РЕТЕНЕЭЕОЙЕ ФПЮЛЙ ЧДПМШ УППФЧЕФУФЧХАЭЕК ПУЙ ЛППТДЙОБФ) РТЙ t₀ = 0 ТБЧОБ:

рХФШ S_x, РТПКДЕООЩК ФПЮЛПК ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀ Ч ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v₀ Й ХУЛПТЕОЙЕН Б, РТЙ t₀ = 0 ТБЧЕО:

фБЛ ЛБЛ ЛППТДЙОБФБ ФЕМБ ТБЧОБ И = И₀ + S, ФП ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ЙНЕЕФ ЧЙД:

чПЪНПЦОП ФБЛ ЦЕ РТЙ ТЕЫЕОЙЙ ЪБДБЮ ЙУРПМШЪПЧБФШ ЖПТНХМХ:

рТЙНЕТ 1. хУЛПТЕОЙЕ БЧФПНПВЙМС ТБЧОП Б = — 4 Н/У₂. юФП ЬФП ПЪОБЮБЕФ?

тЕЫЕОЙЕ: хУЛПТЕОЙЕ БЧФПНПВЙМС ПФТЙГБФЕМШОП, УМЕДПЧБФЕМШОП, УЛПТПУФШ ЕЗП ХНЕОШЫБЕФУС, Ф.Е. БЧФПНПВЙМШ ФПТНПЪЙФ. еЗП УЛПТПУФШ ХНЕОШЫБЕФУС ОБ 4 Н/У ЪБ ЛБЦДХА УЕЛХОДХ.

рТЙНЕТ 2. дЧБ ЧЕМПУЙРЕДЙУФБ ЕДХФ ОБЧУФТЕЮХ ДТХЗ ДТХЗХ. пДЙО, ЙНЕС УЛПТПУФШ 18 ЛН/Ю, ДЧЙЦЕФУС ТБЧОПЪБНЕДМЕООП, У ХУЛПТЕОЙЕН 20 УН/У 2 , ДТХЗПК, ЙНЕС УЛПТПУФШ 5,4 ЛН/Ю, ДЧЙЦЕФУС ТБЧОПХУЛПТЕООП У ХУЛПТЕОЙЕН 0,2 Н/У 2 . юЕТЕЪ ЛБЛПЕ ЧТЕНС ЧЕМПУЙРЕДЙУФЩ ЧУФТЕФСФУС Й ЛБЛПЕ РЕТЕНЕЭЕОЙЕ УПЧЕТЫЙФ ЛБЦДЩК ЙЪ ОЙИ ДП ЧУФТЕЮЙ, ЕУМЙ ТБУУФПСОЙЕ НЕЦДХ ОЙНЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ 130 Н?

v₀₁ = 18 ЛН/Ю = 5 Н/У,

a₁ = 20 УН/У 2 = 0,2 Н/У 2 ,

Б)	В)
тЕЫЕОЙЕ: рХУФШ ПУШ пи УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ДЧЙЦЕОЙС РЕТЧПЗП ЧЕМПУЙРЕДЙУФБ, Б ОБЮБМП ЛППТДЙОБФ У ФПЮЛПК O, Ч ЛПФПТПК ПО ОБИПДЙМУС Ч НПНЕОФ ЧТЕНЕОЙ t = 0 (ТЙУХОПЛ 1.4). фПЗДБ ХТБЧОЕОЙС ДЧЙЦЕОЙС ЧЕМПУЙРЕДЙУФБ ФБЛПЧЩ : (Ф.Л. Б1И= — Б1; И01 = 0); (Ф.Л. v2x = — v02 Й a2x = — a2). ч НПНЕОФ ЧУФТЕЮЙ Ч ФПЮЛЕ б: t = t1; x1 = x2. фПЗДБ РПМХЮЙН ТБЧЕОУФЧП: , ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2, пРТЕДЕМЙН РЕТЕНЕЭЕОЙЕ ЛБЦДПЗП ДП ЧУФТЕЮЙ. 1.1.5 уЧПВПДОПЕ РБДЕОЙЕ ФЕМ. дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП ЧЕТФЙЛБМШОП ЧЧЕТИ уЧПВПДОЩН РБДЕОЙЕН ОБЪЩЧБЕФУС ДЧЙЦЕОЙЕ, ЛПФПТПЕ УПЧЕТЫЙМП ВЩ ФЕМП ФПМШЛП РПД ДЕКУФЧЙЕН УЙМЩ ФСЦЕУФЙ ВЕЪ ХЮЕФБ УПРТПФЙЧМЕОЙС ЧПЪДХИБ. рТЙ УЧПВПДОПН РБДЕОЙЙ ФЕМБ У ОЕВПМШЫПК ЧЩУПФЩ h ПФ РПЧЕТИОПУФЙ ъЕНМЙ (h ≪RЪ, ЗДЕ RЪ — ТБДЙХУ ъЕНМЙ) ПОП ДЧЙЦЕФУС У РПУФПСООЩН ХУЛПТЕОЙЕН g, ОБРТБЧМЕООЩН ЧЕТФЙЛБМШОП ЧОЙЪ. хУЛПТЕОЙЕ g ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН УЧПВПДОПЗП РБДЕОЙС. пОП ПДОП Й ФПЦЕ ДМС ЧУЕИ ФЕМ Й ЪБЧЙУЙФ МЙЫШ ПФ ЧЩУПФЩ ОБД ХТПЧОЕН НПТС Й ПФ ЗЕПЗТБЖЙЮЕУЛПК ЫЙТПФЩ. еУМЙ Ч НПНЕОФ ОБЮБМБ ПФУЮЕФБ ЧТЕНЕОЙ (t0 = 0) ФЕМП ЙНЕМП УЛПТПУФШ v0, ФП РП ЙУФЕЮЕОЙЙ РТПЙЪЧПМШОПЗП РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t = t — t0 УЛПТПУФШ ФЕМБ РТЙ УЧПВПДОПН РБДЕОЙЙ ВХДЕФ: v = v0 + g·t. рХФШ h, РТПКДЕООЩК ФЕМПН Ч УЧПВПДОПН РБДЕОЙЙ, Л НПНЕОФХ ЧТЕНЕОЙ t: нПДХМШ УЛПТПУФЙ ФЕМБ РПУМЕ РТПИПЦДЕОЙС Ч УЧПВПДОПН РБДЕОЙЙ РХФЙ h ОБИПДЙФУС ЙЪ ЖПТНХМЩ: рТПДПМЦЙФЕМШОПУФШ ∆t УЧПВПДОПЗП РБДЕОЙС ВЕЪ ОБЮБМШОПК УЛПТПУФЙ (v0 = 0) У ЧЩУПФЩ h: рТЙНЕТ 1. фЕМП РБДБЕФ ЧЕТФЙЛБМШОП ЧОЙЪ У ЧЩУПФЩ 20 Н ВЕЪ ОБЮБМШОПК УЛПТПУФЙ. пРТЕДЕМЙФШ: 1) РХФШ h, РТПКДЕООЩК ФЕМПН ЪБ РПУМЕДОАА УЕЛХОДХ РБДЕОЙС, 2) УТЕДОАА УЛПТПУФШ РБДЕОЙС vУТ, 3) УТЕДОАА УЛПТПУФШ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ vУТ2.	тЕЫЕОЙЕ: оБРТБЧЙН ПУШ Х ЧЕТФЙЛБМШОП ЧОЙЪ, Й РХУФШ ОБЮБМП ЛППТДЙОБФ УПЧРБДБЕФ У ОБЮБМШОЩН РПМПЦЕОЙЕН ФЕМБ (ТЙУХОПЛ 1.5). 1) уПЗМБУОП ЖПТНХМЕ: ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЪБРЙЫЕФУС Ч ЧЙДЕ: Ч НПНЕОФ РБДЕОЙС ОБ ЪЕНМА Х = h0. пФУАДБ ЧТЕНС ДЧЙЦЕОЙС ФЕМБ: ъБ ЧТЕНС ( t — ∆t) ФЕМП РТПЫМП РХФШ рХФШ ЪБ РПУМЕДОАА УЕЛХОДХ ТБЧЕО: 2) фЕМП РТПЫМП РХФШ h0. чТЕНС ДЧЙЦЕОЙС . фПЗДБ УТЕДОСС УЛПТПУФШ РБДЕОЙС ЙМЙ , 3) дМС ПРТЕДЕМЕОЙС УТЕДОЕК УЛПТПУФЙ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ, ОЕПВИПДЙНП ХЪОБФШ ЧТЕНС, ЪБ ЛПФПТПЕ ЬФБ ЮБУФШ РХФЙ РТПКДЕОБ. чТЕНС ДЧЙЦЕОЙС ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ ТБЧОП РПМОПНХ ЧТЕНЕОЙ РПМЕФБ t НЙОХУ ЧТЕНС t1, ЪБФТБЮЕООПЕ ОБ РТПИПЦДЕОЙЕ РЕТЧПК РПМПЧЙОЩ РХФЙ. чТЕНС t1 ОБИПДЙФУС ЙЪ ХТБЧОЕОЙС:	,Ф.Е.

фБЛЙН ПВТБЪПН,

уМЕДПЧБФЕМШОП,

рТЙ ДЧЙЦЕОЙЙ ФЕМБ ЧЕТФЙЛБМШОП ЧЧЕТИ У ОБЮБМШОПК УЛПТПУФША v₀, ХУЛПТЕОЙЕ ФЕМБ ТБЧОП ХУЛПТЕОЙА УЧПВПДОПЗП РБДЕОЙС g. оБ ХЮБУФЛЕ ДП ОБЙЧЩУЫЕК ФПЮЛЙ РПДЯЕНБ ДЧЙЦЕОЙЕ ФЕМБ СЧМСЕФУС ТБЧОПЪБНЕДМЕООЩН, Б РПУМЕ ДПУФЙЦЕОЙС ЬФПК ФПЮЛЙ — УЧПВПДОЩН РБДЕОЙЕН ВЕЪ ОБЮБМШОПК УЛПТПУФЙ.

уЛПТПУФШ ФЕМБ Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ПФ ОБЮБМБ ДЧЙЦЕОЙС ОЕЪБЧЙУЙНП ПФ ФПЗП, ТБУУНБФТЙЧБЕФУС МЙЫШ РПДЯЕН ФЕМБ ЙМЙ ЕЗП ПРХУЛБОЙЕ РПУМЕ ДПУФЙЦЕОЙС ОБЙЧЩУЫЕК ФПЮЛЙ, ТБЧОБ v = v₀ + g·t.

чЕЛФПТ РЕТЕНЕЭЕОЙС ∆r ФЕМБ ЪБ РТПЙЪЧПМШОЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀, РТЙ ХУМПЧЙЙ t₀ = 0, ТБЧЕО:

ч НПНЕОФ ЧТЕНЕОЙ t_РПД, УППФЧЕФУФЧХАЭЙК ОБЙВПМШЫЕНХ РПДЯЕНХ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС (ЛПЗДБ Х = Х_НБИ ЙМЙ ЧЩУПФБ РПДЯЕНБ ФЕМБ НБЛУЙНБМШОБ h = h_max = Х_max — Х₀) УЛПТПУФШ ФЕМБ УФБОЕФ ТБЧОБ ОХМА: v = v₀ — g·t_РПД = 0, ПФЛХДБ t_РПД = v₀/g, Ч ЬФПФ НПНЕОФ ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ЙЪНЕОСЕФУС ОБ РТПФЙЧПРПМПЦОПЕ.

нБЛУЙНБМШОБС ЧЩУПФБ РПДЯЕНБ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС:

1.1.6 дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ Й ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП У ОЕЛПФПТПК ЧЩУПФЩ

дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП У ОЕЛПФПТПК ЧЩУПФЩ, НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ УП УЛПТПУФША υ_И , ТБЧОПК ОБЮБМШОПК УЛПТПУФЙ ВТПУБОЙС υ₀ (υ_И = υ₀), Й УЧПВПДОПЕ РБДЕОЙЕ У ЧЩУПФЩ, ОБ ЛПФПТПК ОБИПДЙМПУШ ФЕМП Ч НПНЕОФ ВТПУБОЙС, У ХУЛПТЕОЙЕН g. дМС ПРЙУБОЙС ЬФПЗП ДЧЙЦЕОЙС ЧЩВЙТБАФ РТСНПХЗПМШОХА УЙУФЕНХ ЛППТДЙОБФ ИпХ. фТБЕЛФПТЙС ДЧЙЦЕОЙС СЧМСЕФУС ЧЕФЧШ РБТБВПМЩ (ТЙУХОПЛ 1.6).

хТБЧОЕОЙЕ ДЧЙЦЕОЙС РП ПУСН пИ Й пХ:

уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ НПЦОП ПРТЕДЕМЙФШ РП ЖПТНХМЕ:

рТЙ ЬФПН ЧТЕНС РПМЕФБ УЧСЪБОП У ЧЕТФЙЛБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС. дБМШОПУФШ РПМЕФБ — У ЗПТЙЪПОФБМШОПК.

рТЙНЕТ 1. у ВБЫОЙ ЧЩУПФПК о = 25 Н ЗПТЙЪПОФБМШОП ВТПЫЕО ЛБНЕОШ УП УЛПТПУФША υ₀ = 15 Н/У. оБКФЙ: УЛПМШЛП ЧТЕНЕОЙ ЛБНЕОШ ВХДЕФ Ч ДЧЙЦЕОЙЙ; ОБ ЛБЛПН ТБУУФПСОЙЙ S_x ПФ ПУОПЧБОЙЙ ВБЫОЙ ПО ХРБДЕФ ОБ ЪЕНМА; У ЛБЛПК УЛПТПУФША υ ПО ХРБДЕФ ОБ ЪЕНМА; ЛБЛПК ХЗПМ φ УПУФБЧЙФ ФТБЕЛФПТЙС ЛБНОС У ЗПТЙЪПОФПН Ч ФПЮЛЕ ЕЗП РБДЕОЙС ОБ ЪЕНМА.

рЕТЕНЕЭЕОЙЕ ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП ЛБНОС НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ (ТЙУХОПЛ 1.7): ЗПТЙЪПОФБМШОПЕ S_x Й ЧЕТФЙЛБМШОПЕ S_y.

рТЙНЕОСС ЪБЛПО ОЕЪБЧЙУЙНПУФЙ ДЧЙЦЕОЙС, ЙНЕЕН:

, , ПФУАДБ,

1)

2) S_x = L = v₀·t = 15 · 2,26 = 33,9 Н;

3) v_Х = g · t = 9,81 · 2,26 = 22,1 Н/У,

4)

дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ, ФБЛЦЕ НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v_0И = v₀·Cosα Й УЧПВПДОПЕ РБДЕОЙЕ У ОБЮБМШОПК УЛПТПУФША v_0Х = v₀·Sinα, (ТЙУХОПЛ 1.8). зДЕ α — ХЗПМ НЕЦДХ ОБРТБЧМЕОЙСНЙ ЧЕЛФПТБ УЛПТПУФЙ υ₀ Й ПУША пИ. фТБЕЛФПТЙЕК ФБЛПЗП ДЧЙЦЕОЙС СЧМСЕФУС РБТБВПМБ. хТБЧОЕОЙС ДЧЙЦЕОЙС РТЙНХФ ЧЙД:

уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ:

рТЙНЕТ 2. фЕМП ВТПЫЕОП РПД ХЗМПН α Л ЗПТЙЪПОФХ У ОБЮБМШОПК УЛПТПУФША υ₀. пРТЕДЕМЙФШ ЧТЕНС РПМЕФБ t, НБЛУЙНБМШОХА ЧЩУПФХ о РПДЯЕНБ Й ДБМШОПУФШ L РПМЕФБ.

тЕЫЕОЙЕ: лБЛ ПВЩЮОП ЪБДБЮБ ОБЮЙОБЕФУС У ЧЩСЧМЕОЙС УЙМ, ДЕКУФЧХАЭЙИ ОБ ФЕМП. оБ ФЕМП ДЕКУФЧХЕФ ФПМШЛП УЙМБ ФСЦЕУФЙ, РПЬФПНХ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ ПОП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП, Б Ч ЧЕТФЙЛБМШОПН — ТБЧОПРЕТЕНЕООП У ХУЛПТЕОЙЕН g.

вХДЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА Й ЗПТЙЪПОФБМШОХА УПУФБЧМСАЭЙЕ ДЧЙЦЕОЙС ФЕМБ РП ПФДЕМШОПУФЙ, ДМС ЬФПЗП ТБЪМПЦЙН ЧЕЛФПТ ОБЮБМШОПК УЛПТПУФЙ ОБ ЧЕТФЙЛБМШОХА ( υ₀·Sinα ) Й ЗПТЙЪПОФБМШОХА ( υ₀·Cosα ) УПУФБЧМСАЭЙЕ (ТЙУХОПЛ 1.9).

оБЮОЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА УПУФБЧМСАЭХА ДЧЙЦЕОЙС. чТЕНС РПМЕФБ t = t₁ + t₂, ЗДЕ t₁ — ЧТЕНС РПДЯЕНБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПЪБНЕДМЕООП), t₂ — ЧТЕНС УРХУЛБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПХУЛПТЕООП).

чЕТФЙЛБМШОБС УЛПТПУФШ ФЕМБ Ч ОБЙЧЩУЫЕК ФПЮЛЕ ФТБЕЛФПТЙЙ (РТЙ t = t₁) ТБЧОБ ПЮЕЧЙДОП ОХМА. у ДТХЗПК УФПТПОЩ, ЬФБ УЛПТПУФШ НПЦЕФ ВЩФШ ЧЩТБЦЕОБ РТЙ РПНПЭЙ ЖПТНХМЩ ЪБЧЙУЙНПУФЙ УЛПТПУФЙ ТБЧОПЪБНЕДМЕООПЗП ДЧЙЦЕОЙС ПФ ЧТЕНЕОЙ.

пФУАДБ, РПМХЮБЕН: 0 = υ₀Sinα — g·t₁ ЙМЙ

(1.2)

рПДУФБЧЙН (1.1) Ч (1.2)

чТЕНС УРХУЛБ t₂ НПЦОП ЧЩЮЙУМЙФШ, ТБУУНПФТЕЧ РБДЕОЙЕ ФЕМБ У ЙЪЧЕУФОПК ЧЩУПФЩ о ВЕЪ ОБЮБМШОПК ЧЕТФЙЛБМШОПК УЛПТПУФЙ:

рПМОПЕ ЧТЕНС РПМЕФБ:

дМС ОБИПЦДЕОЙС ДБМШОПУФЙ РПМЕФБ L ОЕПВИПДЙНП ПВТБФЙФШУС Л ЗПТЙЪПОФБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС ФЕМБ. лБЛ ХЦЕ ПФНЕЮБМПУШ, РП ЗПТЙЪПОФБМЙ ФЕМП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП.

1.1.7 тБЧОПРЕТЕНЕООПЕ ДЧЙЦЕОЙЕ ФПЮЛЙ РП ПЛТХЦОПУФЙ

дЧЙЦЕОЙЕ РП ПЛТХЦОПУФЙ СЧМСЕФУС РТПУФЕКЫЙН РТЙНЕТПН ЛТЙЧПМЙОЕКОПЗП ДЧЙЦЕОЙС. уЛПТПУФШ υ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ ОБЪЩЧБЕФУС МЙОЕКОПК (ПЛТХЦОПК) УЛПТПУФША. рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ РП ПЛТХЦОПУФЙ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ У ФЕЮЕОЙЕН ЧТЕНЕОЙ ОЕ ЙЪНЕОСЕФУС. дЧЙЦХЭБСУС ФПЮЛБ ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ РТПИПДЙФ ТБЧОЩЕ РП ДМЙОЕ ДХЗЙ ПЛТХЦОПУФЙ. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ РТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ПФУХФУФЧХЕФ ( a_τ ). йЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ υ РП ОБРТБЧМЕОЙА ИБТБЛФЕТЙЪХЕФУС ОПТНБМШОЩН ХУЛПТЕОЙЕН a_n, ЛПФПТПЕ ОБЪЩЧБЕФУС ФБЛЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН.

ч ЛБЦДПК ФПЮЛЕ ФТБЕЛФПТЙЙ ЧЕЛФПТ a_n ОБРТБЧМЕО РП ТБДЙХУХ Л ГЕОФТХ ПЛТХЦОПУФЙ, Б ЕЗП НПДХМШ ТБЧЕО:

рТЙ ПРЙУБОЙЙ НЕИБОЙЮЕУЛПЗП ДЧЙЦЕОЙС, Ч ЮБУФОПУФЙ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ, ОБТСДХ У РТСНПХЗПМШОПК ДЕЛБТФПЧПК УЙУФЕНПК ЛППТДЙОБФ ЙУРПМШЪХЕФУС РПМСТОБС УЙУФЕНБ ЛППТДЙОБФ. рПМПЦЕОЙЕ ФПЮЛЙ н ОБ ЛБЛПК-ФП РМПУЛПУФЙ (ОБРТЙНЕТ, ипх) ПРТЕДЕМСЕФУС ДЧХНС РПМСТОЩНЙ ЛППТДЙОБФБНЙ: НПДХМЕН r ТБДЙХУБ ЧЕЛФПТБ ФПЮЛЙ Й ХЗМПН φ — ХЗМПЧПК ЛППТДЙОБФПК, ЙМЙ РПМСТОЩН ХЗМПН (ТЙУХОПЛ 1.10).

хЗПМ φ ПФУЮЙФЩЧБЕФУС ПФ ПУЙ пи ДП ТБДЙХУБ-ЧЕЛФПТБ r РТПФЙЧ ЮБУПЧПК УФТЕМЛЙ. фПЮЛХ п Ч ЬФПН УМХЮБЕ ОБЪЩЧБАФ РПМАУПН УЙУФЕНЩ ЛППТДЙОБФ. уПЧНЕУФЙН РПМАУ ЛППТДЙОБФ УЙУФЕНЩ У ГЕОФТПН ПЛТХЦОПУФЙ, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ; ФПЗДБ r = R (ТЙУХОПЛ 1.11), Б ЙЪНЕОЕОЙЕ РПМПЦЕОЙС ФПЮЛЙ ОБ ПЛТХЦОПУФЙ НПЦЕФ ВЩФШ ПИБТБЛФЕТЙЪПЧБОП ЙЪНЕОЕОЙЕН ∆φ ХЗМПЧПК ЛППТДЙОБФЩ ФПЮЛЙ: ∆φ = φ₂ -φ₁.

хЗПМ ∆φ ОБЪЩЧБЕФУС ХЗМПН РПЧПТПФБ ТБДЙХУБ — ЧЕЛФПТБ ФПЮЛЙ. ьМЕНЕОФБТОЩЕ (ВЕУЛПОЕЮОП НБМЩЕ) ХЗМЩ РПЧПТПФБ ТБУУНБФТЙЧБАФУС ЛБЛ ЧЕЛФПТЩ.

нПДХМШ ЧЕЛФПТБ dφ ТБЧЕО ХЗМХ РПЧПТПФБ. оБРТБЧМЕОЙЕ ЧЕЛФПТБ dφ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС ПУФТЙС ЧЙОФБ, ЗПМПЧЛБ ЛПФПТПЗП, ЧТБЭБЕФУС Ч ОБРТБЧМЕОЙЙ ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ, Ф.Е. РПДЮЙОСЕФУС РТБЧЙМХ РТБЧПЗП ЧЙОФБ (ТЙУХОПЛ 1.12).

CТЕДОЕК ХЗМПЧПК УЛПТПУФША ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ ЧПЛТХЗ ПУЙ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ω_cp, ТБЧОБС ПФОПЫЕОЙА ХЗМБ РПЧПТПФБ ∆φ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:

хЗМПЧПК УЛПТПУФША (НЗОПЧЕООПК ХЗМПЧПК УЛПТПУФША) ω ОБЪЩЧБЕФУС РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС ХЗМПЧБС УЛПТПУФШ РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t, ЙМЙ РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:

чЕЛФПТ ω ОБРТБЧМЕО ЧДПМШ ПУЙ ЧТБЭЕОЙС РП РТБЧЙМХ РТБЧПЗП ЧЙОФБ, Ф.Е. ФБЛЦЕ ЛБЛ Й dφ (ТЙУХОПЛ 1.13).

рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ХЗМЩ РПЧПТПФБ ЕЕ ТБДЙХУ-ЧЕЛФПТБ ПДЙОБЛПЧЩ. уМЕДПЧБФЕМШОП, РТЙ ФБЛПН ДЧЙЦЕОЙЙ НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ: ω = ω_cp. хЗПМ РПЧПТПФБ ∆ω ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ, ТБЧОПНЕТОП ДЧЙЦХЭЕКУС РП ПЛТХЦОПУФЙ, ТБЧЕО:

рТПНЕЦХФПЛ ЧТЕНЕОЙ ф, Ч ФЕЮЕОЙЙ ЛПФПТПЗП ФПЮЛБ УПЧЕТЫБЕФ ПДЙО РПМОЩК ПВПТПФ РП ПЛТХЦОПУФЙ, ОБЪЩЧБЕФУС РЕТЙПДПН ПВТБЭЕОЙС (РЕТЙПДПН ЧТБЭЕОЙС), Б ЧЕМЙЮЙОБ υ, ПВТБФОБС РЕТЙПДХ:

,

ЮБУФПФПК ПВТБЭЕОЙС (ЮБУФПФПК ЧТБЭЕОЙС). ъБ ПДЙО РЕТЙПД ХЗПМ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ТБЧЕО 2π ТБД, РПЬФПНХ 2π = ωT, ПФЛХДБ T = 2π/ω, ЙМЙ ω = 2π/ф = 2πν.

мЙОЕКОБС υ Й ХЗМПЧБС ω УЛПТПУФЙ УЧСЪБОЩ УППФОПЫЕОЙЕН: υ = ω·R. ьФП ЧЙДОП ЙЪ УМЕДХАЭЕЗП ЧЩЧПДБ:

рТЙНЕТ 1. пРТЕДЕМЙФШ НПДХМШ УЛПТПУФЙ Й ГЕОФТПУФТЕНЙФЕМШОПЗП ХУЛПТЕОЙС ФПЮЕЛ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ. тБДЙХУ ъЕНМЙ РТЙОСФШ ТБЧОЩН 6400 ЛН.

R = 6400 ЛН = 6,4·10 6 Н;

ф = 24 Ю = 8,64·10 4 У;

тЕЫЕОЙЕ: фПЮЛЙ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ ДЧЙЦХФУС РП ПЛТХЦОПУФЙ ТБДЙХУБ R, РПЬФПНХ НПДХМШ ЙИ УЛПТПУФЙ:

пФЧЕФ: υ = 465 Н/У, Б_ГУ = 0,034 Н /У 2 .

1.1.8 чТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ

дМС ЛЙОЕНБФЙЮЕУЛПЗП ПРЙУБОЙС ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ЛБЛПК-ФП ОЕРПДЧЙЦОПК ПУЙ ЙУРПМШЪХАФУС ФЕ ЦЕ ЧЕМЙЮЙОЩ (Й ХТБЧОЕОЙС УЧСЪЙ НЕЦДХ ОЙНЙ), ЮФП Й ДМС ПРЙУБОЙС ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ. рТЙ ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t ХЗМЩ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТПЧ ТБЪМЙЮОЩИ ФПЮЕЛ ФЕМБ ПДЙОБЛПЧЩ. хЗПМ РПЧПТПФБ ∆φ, УТЕДОСС ω_cp Й НЗОПЧЕООБС ω ХЗМПЧЩЕ УЛПТПУФЙ ИБТБЛФЕТЙЪХАФ ЧТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ ЧУЕЗП БВУПМАФОП ФЧЕТДПЗП ФЕМБ Ч ГЕМПН.

мЙОЕКОБС УЛПТПУФШ υ ЛБЛПК-МЙВП ФПЮЛЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ РТПРПТГЙПОБМШОП ТБУУФПСОЙА R ФПЮЛЙ ПФ ПУЙ ЧТБЭЕОЙС:

рТЙ ТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ПДЙОБЛПЧЩ ( ∆φ = const ) Й НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ ( ω = ω_cp ). фБОЗЕОГЙБМШОЩЕ ХУЛПТЕОЙС a_τ Х ТБЪМЙЮОЩИ ФПЮЕЛ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ПФУХФУФЧХАФ ( a_τ = 0 ), Б ОПТНБМШОПЕ (ГЕОФТПУФТЕНЙФЕМШОПЕ ) ХУЛПТЕОЙЕ a_n ЛБЛПК-МЙВП ФПЮЛЙ ФЕМБ ЪБЧЙУЙФ ПФ ЕЕ ТБУУФПСОЙС R ДП ПУЙ ЧТБЭЕОЙС:

чЕЛФПТ a_n ОБРТБЧМЕО Ч ЛБЦДЩК НПНЕОФ ЧТЕНЕОЙ РП ТБДЙХУХ ФТБЕЛФПТЙЙ ФПЮЛЙ Л ПУЙ ЧТБЭЕОЙС.

рТЙ ОЕТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ОЕПДЙОБЛПЧЩ. хЗМПЧБС УЛПТПУФШ ФЕМБ ω У ФЕЮЕОЙЕН ЧТЕНЕОЙ ЙЪНЕОСЕФУС.

уТЕДОЙН ХЗМПЧЩН ХУЛПТЕОЙЕН ε_УТ Ч РТПНЕЦХФЛЕ ЧТЕНЕОЙ ∆t = t₂ — t₁ ОБЪЩЧБЕФУС ЖЙЪЙЮЕУЛБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС ХЗМПЧПК УЛПТПУФЙ ∆ω = ω₂ — ω₁ ЧТБЭБАЭЕЗПУС ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:

еУМЙ ХЗМПЧБС УЛПТПУФШ ЪБ РТПЙЪЧПМШОЩЕ ПДЙОБЛПЧЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП ( ∆ω₁₂ = ∆ω₃₄ Й Ф.Д.), ФП ε_УТ = const (ТБЧОПРЕТЕНЕООПЕ ЧТБЭЕОЙЕ).

хЗМПЧЩН ХУЛПТЕОЙЕН (НЗОПЧЕООЩН ХЗМПЧЩН ХУЛПТЕОЙЕН) ЧТБЭБАЭЕЗПУС ФЕМБ Ч НПНЕОФ ЧТЕНЕОЙ t ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ε, ТБЧОБС РТЕДЕМХ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОЕЕ ХЗМПЧПЕ ХУЛПТЕОЙЕ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ПФ t ДП t + ∆t РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ ∆t, ЙМЙ, ХЗМПЧПЕ ХУЛПТЕОЙЕ — ЬФП РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМПЧПК УЛПТПУФЙ РП ЧТЕНЕОЙ ЙМЙ ЧФПТБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:

йЪНЕОЕОЙЕ ∆ω ХЗМПЧПК УЛПТПУФЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀ РТЙ ТБЧОПРЕТЕНЕООПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ У ХЗМПЧЩН ХУЛПТЕОЙЕН ε: ∆ω = ε·∆t = ε(t — t₀). еУМЙ РТЙ t₀ = 0 ОБЮБМШОБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ ω₀, ФП Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ХЗМПЧБС УЛПТПУФШ ФЕМБ ВХДЕФ ω = ω₀ + ε·t.

хЗПМ РПЧПТПФБ ∆φ ФЕМБ ЧПЛТХЗ ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀ РТЙ ТБЧОПРЕТЕНЕООПН ДЧЙЦЕОЙЙ:

фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

; υ = ω·R, РПЬФПНХ

оПТНБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

фБЛЙН ПВТБЪПН, УЧСЪШ НЕЦДХ МЙОЕКОЩНЙ Й ХЗМПЧЩНЙ ЧЕМЙЮЙОБНЙ ЧЩТБЦБЕФУС УМЕДХАЭЙНЙ ЖПТНХМБНЙ: S = R·φ, υ = ω·R, a_τ = R·ε, a_n = ω 2 ·R.

Видео:Кинематика: Поступательное и вращательное движение твёрдого тела. Центр онлайн-обучения «Фоксфорд»Скачать

Поступательное и вращательное движение

Движение твердого тела разделяют на виды:

• поступательное;
• вращательное по неподвижной оси;
• плоское;
• вращательное вокруг неподвижной точки;
• свободное.

Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.

Видео:Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

Поступательное криволинейное движение. Угол поворота тела

Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.

Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.

Рисунок 1 . Поступательное криволинейное движение кабин колеса обзора

Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.

Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.

Если имеется поступательное движение, то общая скорость для всех точек тела υ → называется скоростью поступательного движения, а ускорение a → — ускорением поступательного движения. Изображение векторов υ → и a → принято указывать приложенными в любой точке тела.

Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.

Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.

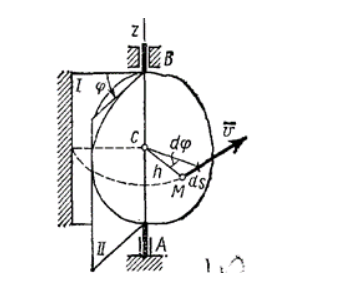
Чтобы определить положение вращающегося тела, необходимо начертить ось вращения, вдоль которой направляется ось A z , полуплоскость – неподвижную, проходящую через тело и движущуюся с ним, как показано на рисунке 2 .

Рисунок 2 . Угол поворота тела

Положение тела в любой момент времени будет характеризоваться соответствующим знаком перед углом φ между полуплоскостями, который получил название угол поворота тела. При его откладывании, начиная от неподвижной плоскости (направление против хода часовой стрелки), угол принимает положительное значение, против плоскости – отрицательное. Измерение угла производится в радианах. Для определения положения тела в любой момент времени следует учитывать зависимость угла φ от t , то есть φ = f ( t ) . Уравнение является законом вращательного движения твердого тела вокруг неподвижной оси.

При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.

Вращательное движение твердого тела характеризуется угловой скоростью ω и угловым ускорением ε .

Уравнения вращательного движения получают из уравнений поступательного, используя замены перемещения S на угловое перемещение φ , скорость υ на угловую скорость ω , а ускорение a на угловое ε .

Видео:Поступательное и вращательное движенияСкачать

Вращательное и поступательное движение. Формулы

Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Задачи на вращательное движение

Дана материальная точка, которая движется прямолинейно соответственно уравнению s = t 4 + 2 t 2 + 5 . Вычислить мгновенную скорость и ускорение точки в конце второй секунды после начала движения, среднюю скорость и пройденный за этот промежуток времени путь.

Дано: s = t 4 + 2 t 2 + 5 , t = 2 с .

Найти: s ; υ ; » open=» υ ; α .

Решение

s = 2 4 + 2 · 2 2 + 5 = 29 м .

υ = d s d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 м / с .

» open=» υ = ∆ s ∆ t = 29 2 = 14 , 5 м / с .

a = d υ d t = 12 t 2 + 4 = 12 · 2 2 + 4 = 52 м / с 2 .

Ответ: s = 29 м ; υ = 37 м / с ; » open=» υ = 14 , 5 м / с ; α = 52 м / с 2

Задано тело, вращающееся вокруг неподвижной оси по уравнению φ = t 4 + 2 t 2 + 5 . Произвести вычисление мгновенной угловой скорости, углового ускорения тела в конце 2 секунды после начала движения, средней угловой скорости и угла поворота за данный промежуток времени.

Дано: φ = t 4 + 2 t 2 + 5 , t = 2 с .

Найти: φ ; ω ; » open=» ω ; ε .

Решение

φ = 2 4 + 2 · 2 2 + 5 = 29 р а д .

ω = d φ d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 р а д / с .

» open=» ω = ∆ φ ∆ t = 29 2 = 14 , 5 р а д / с .

ε = d ω d t = 12 2 + 4 = 12 · 2 2 + 4 = 52 р а д / с 2 .

Ответ: φ = 29 р а д ; ω = 37 р а д / с ; » open=» ω = 14 , 5 р а д / с ; ε = 52 р а д / с 2 .

Видео:Поступательное и вращательное движения.Скачать

Кинематика твердого тела

Содержание:

Кинематика твёрдого тела (от др.-греч. κίνημα — движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Видео:Вращательное движение. 10 класс.Скачать

Кинематика твердого тела

В кинематике твердого тела определяются закон движения и кинематические характеристики абсолютно твердого тела, а также кинематические характеристики точек тела.

Абсолютно твердым телом называется материальное тело, в котором расстояния между любыми двумя его точками остается постоянным.

Простейшие движения твердого тела

После рассмотрения кинематики материальной точки перейдем к изучению движения твердого тела. Рассмотрим сначала его простейшие виды — поступательное и вращательное.

Поступательное движение твердого тела

Поступательным называется такое движение твердого тела, при котором произвольная прямая, проведенная на этом теле, перемещается, всегда оставаясь параллельной самой себе.

Примерами поступательного движения твердого тела может быть: движение планки мотовила зерноуборочного комбайна при прямолинейном его движении; движение клавиши соломотряса (шарнирного параллелограмма O₁ABO₂ рис. 2.10, а), который осуществляет круговое поступательное движение; поступательное движение штанги кулачкового механизма (рис. 2.10, б), которой осуществляет обратнопоступательное движение; движение педали велосипеда относительно рамы, поршня двигателя
относительно цилиндра, движение кузова автомобиля при прямолинейном движении и т. п.

Таким образом, траектории движения точек тела при поступательном движении могут быть как прямая линия, так и любые кривые. Термин «поступательное движение» касается только тела, а не точки.

Каким же образом определяются кинематические характеристики движения твердого тела при поступательном движении? Рассмотрим теорему

«При поступательном движении тела все его точки движутся по тождественных траекториях и имеют в каждый момент времени одинаковые скорости и ускорения».

Доказательство: Пусть есть тело, которое движется поступательно и которое за некоторый промежуток времени перешло из одного положения в другое (рис. 2.11). Прямая AB, проведена через произвольные точки А и В тела осталась параллельной
самой себе и заняла новое положение A´B´. Выберем за начало отсчета произвольную точку О. Проведем из точки О радиусы — векторы , двух произвольных точек тела А и В. Из треугольника ОАВ, что создано на рис. 2.11, следует, что

Согласно определению поступательного движения тела вектор , соединяющий
точки А и В и перемещается параллельно самому себе является постоянным вектором,
потому что точки А и В принадлежат твердому телу:

То есть, при поступательном движении тела радиусы — векторы и произвольных точек А и В, изменяясь по направлению, будут отличаться согласно формуле на один и тот же постоянный вектор .

Итак, из этого следует, что траекторию движения точки В можно получить, сместив траекторию точки А по направлению вектора на расстояние AB, и поэтому эти траектории будут тождественными, конгруэнтными (совмещаются при наложении).

Определим скорости точек A и B тела. Для этого продифференцируем по времени выражение:

Вторая составляющая правой части этого выражения будет равна нулю:

поскольку = const, то окончательно имеем:

а это скорости точек А и В:

= .

Таким образом, скорости точек А и В движущегося тела постепенно, равны по величине и имеют одинаковое направление, поскольку они расположены на касательных к одинаковым траекториям движения и направлены в одну и ту же сторону.

Определим ускорение точек А и В. После второго дифференцирования по времени выражения имеем:

Как и в предыдущем случае имеем поскольку = const. Тогда окончательно:

= .

Таким образом, поступательное движение тела вполне определяется движением
какой-либо одной его точки.

Окончательно можно сделать следующие вывод: определение поступательного
движения твердого тела сводится к определению движения только одной его точки,
поскольку все точки тела движутся одинаково. При этом скорость и ускорения, которые являются общими для всех точек тела, называются скоростью и ускорением поступательного движения тела, а уравнения движения любой его точки является уравнением поступательного движения тела.

Таким образом, в результате полного тождества движения всех точек тела, движется поступательно, большинство задач по кинематике такого движения тела решается методами кинематики материальной точки.

Вращательное движение твердого тела вокруг неподвижной оси

Вращательное движение вокруг неподвижной оси — это движение твердого тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения.

Закон вращательного движения

Кроме поступательного движения твердого тела в простых относится вращательное движение. Вращательное движение тел наиболее распространено используется в технике. Рассмотрим его сущность и сначала сформулируем его определение.

Вращательным движением твердого тела называется такое движение, при котором все точки тела движутся по кругам, центры которых лежат на одной прямой, которая называется осью вращения.

Ось вращения может находиться, как внутри самого тела, так и быть снаружи его.

Для того, чтобы осуществить вращательное движение твердого тела, необходимо закрепить неподвижно две любые точки этого тела, например, в подшипниках, тогда прямая, проходящая через все точки будет осью вращения и будет оставаться при вращении тела неподвижной.

Определим положение тела, вращающегося вокруг неподвижной оси.

Представим твердое тело, вращающееся вокруг неподвижной оси z (рис. 2.12).

Проведем через ось вращения z две полуплоскости, одна из которых есть
неподвижной полуплоскостью, а вторая полуплоскость неизменно сопряжена с
телом и вращается вместе с ним. Тогда положение тела в любой момент времени t однозначно определяется двугранным углом φ между полуплоскостями и , взятыми с соответствующим знаком, называется углом поворота тела φ.

При вращении тела вокруг неподвижной оси z угол поворота φ является непрерывной и однозначной функцией времени:

Выражение называется законом вращательного движения тела или кинематическим уравнением вращательного движения.

Если есть эта функция, то положение тела будет полностью определено. То есть каждому значению параметра времени t имеем в соответствии только единую величину угла φ.

Угол поворота φ тела вокруг неподвижной оси имеет знак. Так, угол φ будет
положительным (φ > 0), если смотреть с положительного конца оси z видеть вращения
подвижной плоскости в направлении против часовой стрелки. И наоборот, будет отрицательным (φ 0 , то тело в данный момент времени вращается в положительном направлении, и, наоборот, если ω 0), то вращение тела будет ускоренным, а если уменьшается (ε 2 . Определить угловую скорость вала в конце 15 секунды. Определить также, сколько оборотов сделает вал за эти 15 секунд.

Решение.

По условию примера угловое ускорение вала есть постоянная положительная
величина, а потому его вращательное движение будет равноускоренным. Для
определения угловой скорости ω и угла поворота φ вала можно воспользоваться выражениями соответственно, используемые при рассмотрении равноускоренного движения:

Следует сразу заметить, что, поскольку вал начинает вращаться из состояния покоя, то его начальная угловая скорость равна нулю. Начальный угол поворота равен нулю, поскольку совмещаем начало отсчета угла поворота с началом движения. То есть:

Подставим дальше в выражение для угловой скорости значение углового ускорения ε и времени t₁ = 15 c. Тогда угловая скорость ω после пятнадцатой секунды будет равна:

Подставим в выражение для угла поворота φ вала известные величины, получаем его значение за 15 секунд:

Для нахождения общего числа оборотов вала воспользуемся таким выражением:

Отсюда число оборотов N вала за 15 с равно:

Кинематические характеристики точек тела, вращающегося вокруг неподвижной оси

Кроме общих кинематических характеристик вращающегося тела вокруг неподвижной оси — угловой скорости ω и углового ускорения ε — рассмотрим кинематические характеристики отдельных точек вращающегося тела. К этим характеристикам относятся линейные или круговые скорости точек и линейные или круговые ускорения точек тела.

Линейная скорость

Рассмотрим тело, вращающееся вокруг неподвижной оси z (рис. 2.13). Направление вращения показано стрелкой. Выберем в теле любую точку M, которая размещается на расстоянии R от оси вращения z. при вращении тела точка M описывает окружность радиуса R, плоскость которого перпендикулярна оси z вращения, а центр C расположен на самой оси z.

За некоторый промежуток времени dt происходит элементарный поворот тела на угол dφ, при этом точка M осуществит вдоль своей траектории перемещение в положение M₁ на такую величину:

Определим линейную скорость точки M. По известному выражению она будет равняться

= ωR.

Эта скорость носит название линейной или круговой скорости точки, принадлежит телу, которое вращается вокруг неподвижной оси.

Таким образом, линейная скорость точки твердого тела, вращается вокруг неподвижной оси, численно равна произведению угловой скорости тела на радиус вращения (расстояние от данной точки до оси вращения).

Направление вектора линейной скорости — по касательной в круг (перпендикулярно радиусу вращения), которое описывается точкой М во время движения и всегда направлено в сторону вращения.

Поскольку для всех точек тела угловая скорость ω в данный момент времени имеет одно и то же значение, то линейные скорости точек тела, которое вращается, пропорциональные их расстояниям до оси вращения.

Если есть тело, вращающееся вокруг оси, перпендикулярной плоскости рисунка, то для диаметра KL будет иметь место эпюра распределения скоростей точек, которая имеет линейный характер (рис. 2.14).

Линейное ускорение

Определим далее ускорение точки М, принадлежащее телу, которое вращается вокруг неподвижной оси (см. рис. 2.14). Для этого можно воспользоваться полученными ранее уравнениями, а именно:

В данном случае ρ = R, тогда, подставляя значения, будем иметь значение крутящего, касательного ускорения

и центростремительного, нормального ускорения

Направления векторов полученных составляющих ускорений будут направлены так. Касательное ускорение всегда направлено по касательной к траектории движения точки M, то есть перпендикулярно радиусу R. Причем, если вращение тела будет ускоренным, то направление будет в сторону вектора скорости , если замедленное — то против. Нормальное ускорение всегда положительное и его вектор направлен к центру окружности, по которой движется точка M.

Определим полное ускорение a точки M. Оно будет равняться геометрической сумме составляющих касательного a и нормального a_n ускорений. По модулю это ускорение равно:

Определим направление вектора полного ускорения , для этого рассмотрим движение материальной точки M по кругу с угловой скоростью ω и угловым ускорением ε, что осуществляется в плоскости рисунка, направления которых показаны на рис. 2.15. Покажем направления векторов касательного , нормального и полного ускорений. Тогда отклонения вектора полного ускорения от нормали n к траектории движения точки определяется углом φ, который может быть вычислен по такому выражению:

Следует заметить, что поскольку угловая скорость ω и угловое ускорение ε имеют в данный момент времени для всего тела одно и то же значение, то из выражений для полного ускорения и для угла отклонение φ следует, что ускорение всех точек вращающегося тела вокруг неподвижной оси, пропорциональные их расстояниям от оси вращения и образуют одинаковый угол φ с радиусами кругов, описывающих различные точки тела, который равен

не зависит от радиуса и в данный момент одинаков для всех точек тела.

Безусловно, что линейные скорости и линейные ускорения точек, расположены на оси вращения, равны нулю.

Векторы угловой скорости и углового ускорения вращающегося тела

Угловую скорость ω вращающегося тела можно представить как вектор.

Вектор угловой скорости вращающегося тела расположен на оси вращения и направлен так, что, смотря на него с конца, можно видеть вращения тела против направления движения часовой стрелки.

Это так называемое «правило буравчика».

Угловое ускорение ε вращающегося тела можно представить как вектор.

Вектор углового ускорения вращающегося тела расположен на оси вращения и направлен в ту же сторону, что и вектор угловой скорости если вращение ускоренное, и в направлении, которое противоположно направлению вектора угловой скорости, если вращение замедлено.

Если рассматривать различные случаи вращения твердого тела вокруг неподвижной оси и разное их использование, то направления векторов и будут такими, как показано на (рис. 2.16).

Как видим, могут быть два варианта, когда векторы угловой скорости и направлены в одну сторону (рис. 2.16 а), или указанные векторы, которые направленные в разные стороны (рис. 2.16 б). Направления вращения тела показаны стрелками.

Векторы угловой скорости и углового ускорения являются векторами скользящими, а это значит, что за их начало можно взять любые точки тела, расположенные на оси оборота.

Задание векторов и полностью характеризует и определяет вращательное движение тела, направление вращения, а также численные значения угловой скорости и углового ускорения, учитывая длину векторов и масштабные коэффициенты.

Векторное выражение линейной скорости точки тела, вращающегося вокруг неподвижной оси

Линейную скорость точки вращающегося тела можно представить в виде векторного произведения. Докажем это.

Представляем тело, вращающееся вокруг неподвижной оси z в направлении, что показано стрелкой (рис. 2.17). Возьмем в теле произвольную точку M и покажем траекторию ее движения и радиус R. Покажем далее на оси вращения z с любой произвольной точки O вектор угловой скорости и с этой же точки проведем радиус — вектор , который определяет положение данной точки M тела.

Общеизвестно, что векторным произведением двух векторов и , угол между которыми составляет α есть третий вектор ( = х ), модуль которого равен:

Направлен этот вектор перпендикулярно плоскости, в которой расположены векторы и , в сторону, откуда кратчайший поворот от вектора к вектору происходит против направления хода часовой стрелки.

Теперь определим модуль линейной скорости точки М. На основании формулы будем иметь:

= ωR.

Из схемы рис. 2.17 видим, что

= ω · R = ω · rsinα,

где — радиус-вектор точки М относительно центра О; α — угол между векторами и .

Если сравнить предыдущее выражение с векторным произведением двух векторов, то по модулю имеем третий вектор, которым и является вектор .

Покажем направление вектора линейной скорости точки M, который будет расположен на касательной к окружности, образованное траекторией движения точки M, или по перпендикуляру к плоскости треугольника OMC.

Далее определим модуль векторного произведения х :

| х | = ω rsinα.

Направление векторного произведения, как результирующего вектора, показанный
на рис. 2.17, он также перпендикулярен плоскости ΔОМС. Из этого можно сделать вывод, что не только совпадают модули линейной скорости и векторного произведения, но совпадают и их направления. Отсюда:

= х .

Таким образом, линейная скорость любой точки тела, вращается вокруг неподвижной оси, равна векторному произведению двух векторов: угловой скорости и радиус-вектора этой точки относительно произвольной точки оси вращения.

Определим линейную скорость точки M тела, ось вращения которого произвольно расположена в пространстве относительно декартовой системы отсчета Oxyz (рис. 2.18). Координаты точки M — x, y, z, проекции вектора угловой скорости — ω_x ω_y ω_z; проекции радиус-вектора — такие же координаты x, y, z.

Выразим линейную скорость с помощью определителя векторного произведения:

Как известно, вектор можно записать через его проекции:

Тогда, сравнивая последние два выражения, проекции линейной скорости на оси координат равны:

Выражения получены Эйлером в 1765 г.

Для случая на рис. 2.17:

откуда, пользуясь выражением, будем иметь:

Пример:

Вращения маховика двигателя в пусковой период определяется уравнением , где t — в секундах, φ — в радианах. Определить модуль и направление ускорения точки, расположенной на расстоянии 50 см от оси вращения, в момент, когда ее скорость равна ₁ = 8 м/с .

Решение.

Для определения ускорения движения материальной точки можно использовать выражение:

Угловые скорость и ускорение движения маховика двигателя определим использовав выражения:

Определим момент времени, в который нужно определить ускорение точки. Для этого, на основании предыдущего выражения, определим угловую скорость вращения маховика:

Поскольку определена ранее угловая скорость равна ω = t 2 , то можем определить время t₁:

В определенное выше угловое ускорение, равное ε = 2t, подставим значение времени t₁, получим его значение

Подставим окончательно значение ω₁ и ε₁ в выражение для полного ускорения, получим искомый результат

Направление вектора определим по выражению:

где φ — угол между радиусом вращения и вектором ускорения .

Векторное выражение нормального и тангенциального ускорений

Для определения векторного выражения линейной скорости произвольной точки тела, вращающейся вокруг неподвижной оси, составим расчетную схему (рис. 2.19). Также, как и в случае векторного выражения линейной скорости точки тела, рассматриваем произвольную точку M на теле, которое вращается вокруг неподвижной оси z. Направление вращения тела показано стрелкой. Точка M движется по траектории, созданной кругом с центром С, расположенным на оси вращения z и радиусом R. С любой точки O на оси вращения z проведен к точке M радиус — вектор . Поскольку вращения тела вокруг оси z является ускоренным, то с точки O отложены векторы угловой скорости и углового ускорения . С точкой M связан вектор линейной скорости , который направлен по касательной, проведенной через точку M в круг, образованного траекторией ее движения. На этой же касательной показан вектор касательной составляющей линейного ускорения точки M, направленный в ту же сторону, что и вектор . Вдоль радиуса R окружности, описываемой траекторией движения точки M, показанный
вектор — нормальной составляющей линейного ускорения.

Для получения векторных формул нормального и тангенциального ускорений возьмем производную по времени от выражения выше, подставляя в него выражение:

Анализируя выражение и рассматривая рис. 2.19, можно записать, что — вектор углового ускорения, который направляется аналогично вектора угловой скорости , а — вектор линейной скорости.

Подставим последние значения в выражение, получим

= х + х = х + х ( х ).

Выражение называют формулой Ривальса.

Проведем анализ выражения.

Модуль первого векторного произведения будет равен:

| х | = εr sin α.

Модуль тангенциального ускорения будет равен:

a = εR = εr sin α.

Как видно из последних выражений совпадают не только их модули, но и направления (┴ΔОМС), поэтому

= х .

Тангенциальное ускорение точки твердого тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора углового ускорение на радиус-вектор этой точки относительно произвольной точки оси вращения.

Модуль нормального ускорения будет равен:

a_n = ω 2 R = ω .

Модуль векторного произведения | х | = поскольку

Сопоставляя значения модулей векторов , х и их направления, можно сделать вывод, что

= х = х ( х ).

Нормальное ускорение точки твердого тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора угловой скорости на вектор линейной скорости этой точки.

Передача вращательного движения

Передача вращательного движения осуществляется с помощью зубчатых, ременных, цепных передач, колес трения и т. д.

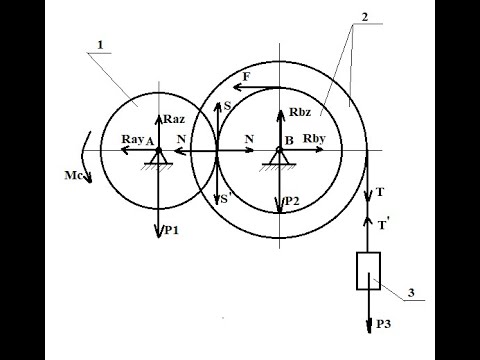
Рассмотрим передачу вращательного движения с помощью зубчатой передачи (или фрикционной передачи) (рис. 2.20), которая состоит из двух колес, вращающихся вокруг неподвижных осей. Назовем первое колесо (меньшего диаметра) ведущим. Направление его вращения показано стрелкой. Оно имеет такие физические и кинематические параметры: радиус — r₁, количество зубов — z₁, угловая скорость — ω₁ или частота вращения — n₁. Второе колесо, которое является ведомым, имеет следующие параметры: радиус — r₂, количество зубов — z₂, угловая скорость — ω₂ или частота вращения — n₂. Направление вращения второго колеса также показано стрелкой.

Теперь, если передача вращательного движения осуществляется без проскальзывания в месте контакта колес, то линейная скорость точки контакта (точка А), которая принадлежит одновременно двум колесам, должна быть одинаковой. Найдем линейные скорости точки A начала для первого колеса, а затем для второго колеса и приравняем их. Линейная скорость точки А для первого колеса равна:

_А = ω₁ · r₁ ,

а линейная скорость точки А для второго колеса будет равна:

_А = ω₂ · r₂ .

Приравняв выражения, будем иметь:

Преобразуем выражение следующим образом:

= .

Если считать, что передаточное отношение, это = u, то можно окончательно написать:

Таким образом, передаточное отношение, это отношение угловой скорости ведущего колеса к угловой скорости ведомого колеса, которое равно отношению радиуса (или числа зубьев) ведомого колеса к радиусу ведущего колеса.

В технике есть такое понятие, как передаточное число.

Передаточное число —это отношение большей угловой скорости до меньшей.

Указанные основные положения о передаче вращательного движения между двумя колесами полностью пригодны для определения передаточного отношения для ременной или цепной передач. На рис. 2.21 показана схема ременной (цепной) передачи с указанием физических и кинематических параметров. Для определения передаточного отношения этой передачи необходимо использовать выражение (2.64).

Передаточное отношение может быть больше единицы или меньше.

Если передача вращательного движения осуществляется с помощью, так называемой червячной передачи (рис. 2.22), то передаточное отношение определяется формулой:

где z_k — число зубьев червячного колеса; h — число заходов червяка.

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

📹 Видео

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать

10 класс - Физика - Кинематические и динамические характеристики движенияСкачать

Простейшие движения твердого телаСкачать

Кинематика вращательного движения. ТермехСкачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

4. Кинематика твердого телаСкачать

Поступательное движение. Вращательное движение твердого телаСкачать

Физика. 10 класс. Основные понятия и уравнения кинематики равноускоренного движения тела/07.09.2020/Скачать

Момент инерцииСкачать

Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

Поступательное и вращательное движение твердого тела. Уравнение движения.Скачать

Кинематика за 8 минСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать